Hydrodynamic Analysis of Coating Stability in Slot-Die Coating Processes

Abstract

Slot-Die coating, has been widely applied in flexible electronics, functional films, micro-nano manufacturing and circuit production because of its fast production speed, low cost, and large-area coating available. In this paper, the fluid dynamic finite element analytical methodology was used to analyze the initial flow field of the slot-die coating produced by the anode slurry of lithium-ion battery on the copper foil substrate. Based on the theoretical analysis of the Navier-Stokes equations on the dynamics of the initial flow field at the coating head, a theoretical model of the flow rate, the flow relationship, and various pressure differences between the upstream and downstream of the coating beads was established. The flow mechanism of the coating layer was also revealed. Considering the inertia effect, the coating stability was predicted by applying the viscous capillary model. This study can contribute to the theoretical foundation for further improvement of the stability of slit coating.

1 Introduction

Slot-die coating (SDC) is an advanced predictive coating technology in which all the fluid fed into the extrusion die head forms a coating on the substrate [1]. In the actual process, the uniformity, stability, edge, and surface effect of coating solution are affected by the rheological properties of coating solution, which directly determines the quality of coating [2]. Schmit et al. [3] studied the stability of the coating edge in the process of lithium-ion battery cathode paste extrusion coating and discovered the phenomenon that intermittent coating and continuous coating process led to the issue of thick edge. Ruschak [4] analyzed the initial flow field at the coating head and proposed a viscous capillary model. On this basis, Higgins [5] considered the influence of Couette flow and Poiseuille flow and predicted the minimum coating thickness achieved under different parameters. Lee et al. [6] used the VC model to study the SDC process of Newtonian and non-Newtonian fluids through frequency response analysis and analyzed the effects of process parameters on fluid behavior, such as lip structure, material properties, operating conditions, etc. In this paper, a mathematical model is established to simulate and verify the initial process of coating graphite anode slurry of Lithium-ion battery, analyze the stability of the slurry coating process, observe the fluid flow characteristics at the initial coating stage, and study the influence of different process parameters on coating stability. This research aims to provide theoretical support for coating process optimization.

2 Establishment of Mathematical Model and Theoretical Analysis

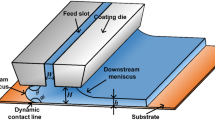
The slurry is transported to the reservoir through the feeding channel and then flows equably from the slit. When the slurry reaches the substrate, due to the relative speed between the coating head and the substrate, the slurry on the substrate will be stabilized after the temporal accumulation and will form the meniscus, which then transform into the liquid bridge because of the relative motion between the coating of the slit and the substrate. The liquid held between the upper lip of the slit and the substrate is called the coating bead whose flow field is shown in Fig. 1.

Fig. 1.

Schematic of slot coating

After the coating is stable, the shape of the coating bead is constant and the flow process can be regarded as the steady flow of the viscous incompressible fluid. The flow field of the coating bead is analyzed by applying the differential motion equation of the viscous incompressible fluid, namely, the N – S equation, the flow process is three-dimensionally steady.

The state of the fluid in this paper is laminar flow. Because the coating width is much larger than the gap height, the direction Z is mainly considered. So we can get,

$$ u = \frac{{y^{2} }}{2\mu } \cdot \frac{\partial p}{{\partial x}} + C_{1} \cdot z + C_{2} $$

(1)

Approximately assuming that $\frac{\partial p}{{\partial x}} = \frac{{d_{p} }}{{d_{x} }} = \frac{\Delta p}{l}$, among them:

$$ \left\{ {\begin{array}{*{20}l} {{\text{ upstream: }}\frac{\Delta p}{l} = \frac{{p_{2} - p_{3} }}{{l_{1} }}} \hfill \\ {{\text{ downstream: }}\frac{\Delta p}{l} = \frac{{p_{4} - p_{5} }}{{l_{2} }}} \hfill \\ \end{array} } \right. $$

(2)

In formula (1), C₁ and C₂ are integral constants, which can be solved by taking into specific boundary conditions. The fluid-solid interface is a non-slip boundary condition. Therefore, when $z = 0$, $u = 0$; when $z = h_{m}$, $u = U_{c}$. Taking them into formula (1) we obtain:

$$ C_{2} = 0,C_{1} = \frac{{U_{c} }}{{h_{m} }} \cdot \left( {1 - \frac{\Delta p}{{2\mu l}}} \right) $$

(3)

$$ u = \frac{{U_{c} }}{{h_{m} }} \cdot z - \frac{{z \cdot \left( {h_{m} - z} \right)}}{2\mu } \cdot \frac{\Delta p}{l} $$

(4)

Flow changes during the coating process can be represented as Q.

$$ Q = \int\limits_{0}^{H} {u \cdot b \cdot {\text{d}}z} $$

(5)

Taking Eq. (4) into Eq. (5) we obtain:

$$ Q = - \frac{{bH^{3} }}{12\mu } \cdot \frac{\Delta p}{l} + \frac{bH}{2} \cdot U_{c} $$

(6)

After the coating is stable, the upstream shape of the coating bead is also stable. The flow rate of the upstream coating bead is 0. The amount of fluid entering at the inlet is equal to the flow increment of the coating downstream, that is:

$$ Q_{{\text{up }}} = 0,\quad Q_{{\text{down }}} = U_{c} \cdot b \cdot h_{m} $$

(7)

Substituting Eqs. (2) and (7) into Eq. (6), we simplify the model to a 2D model. Two pressure differences can be obtained as follows:

$$ \left\{ {\begin{array}{*{20}l} {p_{2} - p_{3} = - \frac{{6l_{1} \mu U_{c} }}{{H^{2} }}} \hfill \\ {p_{4} - p_{5} = - \frac{{12l_{2} \mu U_{c} }}{{H^{3} }}\left( {h_{m} - \frac{H}{2}} \right)} \hfill \\ \end{array} } \right. $$

(8)

The pressure difference upstream the coating bead is determined by the Young-Laplace equation. The shape upstream of the coating bead is approximately an arc. The static contact angle between the upstream of the coating bead and the substrate is $\theta$. The static contact angle between the upstream of the coating bead die and the substrate is $\phi$. Therefore, the pressure drop here is:

$$ p_{1} - p_{2} = - \frac{\sigma }{H}(\cos \theta + \cos \phi ) $$

(9)

For the pressure difference at the meniscus downstream of the coating bead, it can be derived from the Landau–Levich film equation [7]:

$$ p_{5} - p_{6} = - 1.34\left( {\frac{{\mu U_{c} }}{\sigma }} \right)^{2/3} \frac{\sigma }{h} $$

(10)

For the stabilized coating, since the coating is thin and exposed to air, the pressure can be considered to be evenly uniform. In previous studies, in the viscous capillary model we assumed that the pressure difference at the exit of the slit was 0. That is $p_{4} - p_{3} = 0$. Therefore, the length $l_{1}$ can be deduced.

$$ \begin{aligned} l_{1} = & \frac{{H^{2} }}{{6\mu U_{c} }}\left\{ {p_{6} - p_{1} - 1.34\left( {\frac{{\mu U_{c} }}{\sigma }} \right)^{2/3} \frac{\sigma }{{h_{m} }} - \frac{{12l_{2} \mu U_{c} }}{{H^{3} }}\left( {\frac{H}{2} - h_{m} } \right)} \right. \\ & \left. { - \frac{\sigma }{H}(\cos \theta + \cos \phi )} \right\} \\ \end{aligned} $$

(11)

When the upstream length is close to 0, it is easy for the air to enter the coating beads intermittently, which leading to uneven coating or even coating defects [8]. In most theoretical studies, $l_{1} = 0$ is considered as the critical condition and minimum coating condition for coating stability, where the value of l₁ is related to the pressure difference around the coating bead. To ensure the accuracy of the model, the pressure difference at the exit of the gap, i.e., $p_{4} - p_{3}$ should also be considered.

The flow process between p₃ and p₄ in the slot exit is approximately Couette flow. Its pressure changes basic equation is $\frac{{{\text{d}}p}}{{{\text{d}}x}} = \mu \frac{{{\text{d}}^{2} u}}{{{\text{d}}z^{2} }}$. After integrating this equation, the formula is as follows,

$$ u = \frac{1}{2\mu }\frac{{{\text{d}}p}}{{{\text{d}}x}}z^{2} + C_{1} z + C_{2} $$

(12)

Its boundary conditions are: $z = 0,u = U_{c}$; $z = H,u = 0$. Taking them into Eq. (12), we get,

$$ u = \frac{1}{2\mu }\frac{{{\text{d}}p}}{{{\text{d}}x}}\left( {z^{2} - H} \right) - \frac{{U_{c} \cdot z}}{H} + U_{c} $$

(13)

Then the flow rate of the section is as follows,

$$ Q = \int\limits_{0}^{H} {u{\text{d}}z} = \frac{{U_{c} H}}{2} - \frac{{H^{3} }}{12\mu }\frac{{{\text{d}}p}}{{{\text{d}}x}} = U_{c} \cdot h_{m} $$

(14)

Approximately $\frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{\Delta p}{W}$, $\Delta p = p_{4} - p_{3}$, Then,

$$ p_{3} - p_{4} = \frac{{12\mu U_{c} W}}{{H^{3} }}\left( {\frac{H}{2} - h_{m} } \right) $$

(15)

After considering this pressure difference, the length $l_{1}^{\prime }$ upstream the coating bead can be deduced as:

$$ l_{1}^{\prime } = l_{1} + \frac{2W}{H}\left( {\frac{H}{2} - h_{m} } \right) $$

(16)

3 Numerical Simulation

3.1 Simulation Parameter Setting

In the coating flow field, the Reynolds number is 0.0435, so the laminar flow model is selected, assuming that the viscosity of the slurry does not change. The material parameters of the anode slurry, the geometric parameters of the die and the process parameters are shown in Table 1, in which the slurry inlet velocity is respectively selected as 0.020, 0.035, and 0.050 m/s, and the coating speed is selected as 0.10, 0.15 and 0.20 m/s to study the influence of different process parameters on the coating stability [10].

3.2 Analysis of Simulation Results

In this paper, the finite element analysis is performed using Fluent19.0, and the simulation parameters are set according to the coating process parameters in Table 1. When the coating speed is set as 0.15 m/s, Fig. 2 a, b and c are the fluid flow states from the start of coating to the steady state when the slurry inlet velocity is 0.020 m/s, 0.035 m/s and 0.050 m/s, respectively. And it can be observed from the figure that when the inlet velocity is 0.020 m/s, the coating bead is the smallest. So there is insufficient material supply or even a fracture at the downstream; when the inlet velocity is 0.035 m/s, the entire coating process is relatively stable, and the coating can reach a stable state; When the inlet velocity is 0.050 m/s, slurry accumulation occurs at the upstream and the coating is too thick at the downstream, hence it is difficult for the coating process to reach a stable state.

Table 1. Main parameters

When the inlet velocity is set as 0.035 m/s, Fig. 2 d and e show the fluid flow states from the start of coating to the steady state when the coating velocity is 0.10 m/s and 0.20 m/s, respectively. It can be observed from the figure that when the coating speed is 0.10 m/s, the slurry accumulates at the upstream and the coating is too thick at the downstream; When the coating speed is 0.20 m/s, the coating bead is the smallest and it is difficult to achieve a stable coating state, and there is insufficient material supply or even a fracture in the downstream.

Fig. 2.

Variation of slurry flow with time under different process parameters

It can be observed from Fig. 3 that if the coating speed is too high or if the inlet speed is too low, the length of the upstream of the coating bead will be less than 0, which will easily lead to gas entrainment into the coating, resulting in bubbles. At the same time, the coating layer will be unevenly distributed and the coating will be too thin. When the coating speed is too low or the inlet speed is too high, slurry accumulation occurs upstream the coating bead, resulting in large change in the pressure difference across the coating bead, and the coating layer is too thick and uneven, which cannot meet the process requirements. When the inlet velocity is 0.035 m/s and the coating velocity is 0.15 m/s, the coating can quickly reach a stable state. When the coating tends to be stable, the length of the upstream of the coating bead reaches the minimum and is greater than 0, and the slurry volume at the upstream also reaches the minimum.

Fig. 3.

Fluid distribution in stable coating state with different process parameters

The change of the volume fraction upstream of the coating bead can be monitored, as shown in Fig. 4 a. After about 0.3s, the volume fraction of the slurry hardly changes, that is, the coating process reaches a stable state. At the same time, the change of static pressure at the inlet is calculated, as shown in Fig. 4 b, and the change trend is consistent with the change trend of the volume fraction of the slurry.

After comparing several groups of simulation data with the calculated data, it is found that when the static pressure at the inlet no longer changes, the volume upstream the coating beads reaches the minimum. That is, the length l₁ reaches the minimum. Combining the two curves together as shown in Fig. 4 c, we can observe that the two have the same change trend with time.

Fig. 4.

Static pressure at the inlet and volume fraction upstream the coating beads with time

The inlet static pressure changes with time in the case of Fig. 2 a, c, d, e, are calculated, and the calculation results are shown in Fig. 5 a, b, c, d respectively.

Fig. 5.

Curve of inlet static pressure changes with time under different process parameters

It can be seen from the figure that when the inlet speed is too low or the coating speed is too high, the static pressure at the inlet changes little but it is difficult to achieve stability; When the inlet speed is too high or the coating speed is too low, the static pressure at the inlet changes rapidly. Though stability is achieved rapidly, the value is large, resulting in excessive pressure on the substrate and easy accumulation of slurry. Therefore, a relatively stable coating process can be obtained only by selecting appropriate process parameters.

4 Conclusion

The N-S equation is applied and simplified in terms of the actual boundary conditions in this paper to theoretically analyze the upstream section and deduce the flow velocity and flow distribution formulas in the upstream and downstream sections. Using the viscous capillary model, the stability of the coating is predicted considering the influence of inertial effect. By the aforementioned numerical and simulation analysis, the conclusions are as follows.

• 1) When the inlet speed is 0.035 m/s, the coating layer can quickly reach a stable state. It is also found that when the coating speed is 0.15 m/s, the coating effect is the best, and the coating layer can quickly reach a steady state.

• 2) The variation law of the length at l₁ position is the same as that of the static pressure at the entrance. Therefore, the pressure change at the entrance can be observed and measured. When the static pressure change tends to be stable, the coating layer reaches a stable state.