Keywords

1 Introduction

The history of numerous natural and manmade slope failures due to earthquakes has fetched significant awareness from researchers and scientists for analyzing seismic slope stability more rigorously. Kramer [1] and Wang et al. [2] mentioned that the appropriate analysis of seismic slope stability is very challenging and stimulating. The available techniques for the analysis of seismic slope stability are ranging from the pseudo-static method to the failure mass movement approach (e.g., Newmark’s rigid block method), in addition to some recently developed advanced methods like the pseudo-dynamic method, modified pseudo-dynamic method, and stress deformation method based on finite elements [3, 4]. Out of all the methods, displacement-based methods provide a rational idea about the functioning of slopes during earthquake shaking as the serviceability of slope is operated by the post-earthquake deformation [5]. The first displacement method was proposed by Newmark [6] based on the concept of rigid block sliding on a tilted surface. Thereafter, by adopting Newmark’s theory many displacement-based predictive models have been developed in recent studies [7,8,9,10,11] using real ground motion. Most of these studies neglect the impact of vertical component of seismic forces by assuming that a decrease in the seismic factor of safety is resulting from a singular act of the horizontal earthquake loading component. Apart from the displacement-based methods, various analytical approaches have been established in the earlier studies based on limit equilibrium and the limit analysis technique [12,13,14,15,16,17] to assess the seismic slope stability. However, in earlier studies, the impact of vertical seismic acceleration has not been considered and a conclusive remark has been made that under the earthquake condition horizontal component of the seismic inertia forces is only engaged in the failure of slopes.

In this study, a pseudo-static stability assessment using the finite element method has been carried out by accounting combined impact of horizontal and vertical components of earthquake forces. The pseudo-static technique is a simple method, and the computation of the stability is similar to the traditional static stress calculation, no sophisticated evaluation is therein required [1]. Earlier, Choudhury et al. [4], Choudhury and Modi [18], Chatterjee and Choudhury [19] had applied the pseudo-static method for slope stability analysis. Further, Sangroya and Choudhury [20] used pseudo-static analysis in the finite-difference program FLAC3D to investigate the slope stability under dynamic loading. Similarly, in this paper, the behavior of slopes against seismic loading was demonstrated via seismic safety factor and displacement. Also, the minimum pseudo-static acceleration required for failure i.e., yield acceleration was estimated under the combined seismic acceleration. Further, the overall impact of combined seismic loading on slope stability has been presented through a set of parametric studies. Finally, the safety factor computed by employing the numerical analysis was compared with that calculated using analytical analysis based on the sliding block mechanism. The study describes the significance of vertical seismic acceleration in the dynamic slope stability assessment to lessen down the earthquake-induced geo-calamities.

2 Methodology

2.1 Finite Element Slope Model

For the numerical analysis, a hypothetical model of slope, as depicted in Fig. 1, was developed using the finite element computer program PLAXIS 2D [21]. The two-dimensional plane strain condition was considered to model the slope section. The whole model was discretized with 15 nodded trilateral elements with twelve Gaussian points, available in the PLAXIS library. These elements were used to generate gravity load, stress redistribution and the stiffness matrix for simulating the accurate behavior of soil under seismic loading conditions. The constitutive model for soil material was assumed as elastic perfectly plastic which fails under the Mohr-Coulomb failure principle. The height of the slope was considered as 10 m. Below the slope a 3 m deep foundation was included to observe whether the failure zone passes across the slope base. The slope inclination angle \(\left( \beta \right)\) was considered as \(60^\circ\). The lateral extent of the slope model was kept as 20 m to diminish the boundary effect due to seismic loading. The groundwater table (GWT) was presumed to be situated at the slope toe, 10 m below the slope top.

Boundary conditions are constraints necessary for solving a finite-element-based boundary value problem. In the present finite element model, boundary conditions were selected in such a manner that the impact of stress distribution can be reduced. In order to simulate the model under semi-infinite conditions, at the base of the slope a fixed boundary was applied, whereas the roller boundaries were assigned at the sides. This type of boundary condition allows the slope model to move freely vertically but restricts the movement laterally [22]. The size of the mesh is frozen after numerous iterations. This process is called mesh optimization, and this ensures that further finer mesh will not impact much on the output of analysis rather than time-consuming. As a result, 940 elements with 7729 nodes were formed in the slope mesh. The discretized finite element slope model with boundary conditions is shown in Fig. 1.

Fig. 1.
figure 1

Finite element slope model with discretized mesh and boundary conditions.

Full size image

The assumed index and engineering soil parameters utilized in the present analysis are presented in Table 1. The elastic properties of soil material have less impact in the estimation of the safety factor as compared to the soil deformation characteristics [23]. Therefore, due to a lack of meaningful data, the value of Elasticity modulus and Poisson’s ratio was taken from Griffiths and Lane [24]. Griffiths and Marquez [25] reported that the slope stability assessment is a comparatively unconfined problem where zero angle of dilation subject to no volume change of soil at the time of yielding may be assumed. Hence, in this study, the dilation angle was taken as zero.

Table 1. Input soil parameters for present study.
Full size table

2.2 Framework for Pseudo-Static Stability Analysis

Terzaghi [26] proposed the first comprehensive utilization of the pseudo-static slope stability analysis. This stability method defines the impacts of ground motion by constant horizontal or vertical accelerations that produce horizontal and vertical inertial forces, acting through the centroid of the failed soil mass [19]. Analytically the horizontal and vertical pseudo-static forces can be expressed as [1]:

$$ F_H = \frac{A_h W}{g} = \alpha_h W $$
(1)
$$ F_V = \frac{A_v W}{g} = \alpha_v W $$
(2)

Where, \(A_h\) and \(A_v\) are the horizontal and vertical pseudo-static acceleration respectively; \(W\) is the weight of the failure mass; \(\alpha_h\) and \(\alpha_h\) are the dimensionless horizontal and vertical pseudo-static acceleration coefficient respectively.

In this study, the pseudo-static method was employed to analyze the slope stability using the PLAXIS 2D [21] computer program. The combined loading of horizontal and vertical pseudo-static forces was applied to the whole finite element mesh. The pseudo-static analysis significantly depends on the value of seismic coefficients as those acts in directions that generate positive driving moments [1, 27, 28]. Therefore, in this study, a range of horizontal and vertical seismic coefficients was considered in order to understand their influence on slope stability. By entering a specified value of the pseudo-static coefficient, the analysis was carried out in 3 phases. Phase I is the initial phase in which the model was subjected to gravity load, where the forces of each element were accumulated into a global gravitational force vector to evaluate the initial state of stress. Phase II is the plastic analysis phase, which evaluates the incremental stresses generated in the soil due to dynamic loading and slope instability, and Phase III is the safety analysis phase which evaluates the factor of safety of slopes using the strength diminution technique. In this approach, the two soil parameters \(c^{\prime}\) and \(\tan \phi^{\prime}\) are successively reduced by the strength reduction factors till failure of the slope takes place. The least magnitude of this factor for which failure happens is called safety factor of the slope [29]. The reduced strength parameters can be determined from the equation given by Matsui and San [30]:

$$ c^{\prime}_r = \frac{{c^{\prime}}}{R_f } $$
(3)
$$ \phi^{\prime}_r = \arctan \left( {\frac{{\tan \phi^{\prime}}}{R_f }} \right) $$
(4)

where \(R_f\) is the reduction factor; \(c^{\prime}_r\) and \(\phi^{\prime}_r\) are the reduced effective cohesion and reduced friction angle, respectively. At the initial stage of the analysis, a very small value of \(R_f\) was considered (0.01) such that the strength parameters remain big enough to remain the slope in an elastic state. \(R_f\) increases progressively till the failure, which indicates that the elastic-plastic finite element computation fails to satisfy a physical convergence criterion.

3 Results and Discussion

Different magnitudes of horizontal and vertical seismic acceleration and their combination were applied to the slope model. Thereafter, the yield acceleration was decided as the seismic coefficient at which the slope fails. The yield acceleration is a function of \(\alpha_v\) for a particular magnitude of \(\beta\) and \(\phi^{\prime}\) for slope under joint seismic loading [23]. Hence, to find out a constant value of yield acceleration the \(\alpha_v\) was kept as 0 and the value of \(\alpha_h\) was increased monotonically. Finally, the yield acceleration for the particular slope was reported in terms of horizontal yield seismic coefficient (\(\alpha_{hy}\)) at which the factor of safety (FS) went below 1. It was found that at \(\alpha_h\) = 0.1 and \(\alpha_v\) = 0, the FS of the slope was 0.984. Therefore, 0.1 can be considered a horizontal yield seismic coefficient (\(\alpha_{hy}\)) for the particular slope. Figure 2 shows the displacement profile of the slope for \(\alpha_{hy}\) = 0.1. From the figure, it can be observed that at the failure a prominent failure zone developed throughout the face of the slope (from crest to toe). The maximum displacement under pseudo-static condition was computed as 4.42 mm.

Fig. 2.
figure 2

Displacement profile of the slope corresponding to \(\alpha_{hy} = 0.1\).

Full size image

A set of parametric studies was performed considering a few soil and seismic parameters to comprehend the impact of combined seismic loading on the slope stability. Figure 3 portrays the variation of FS with the horizontal seismic coefficient for different magnitudes of \(\alpha_v\). It was observed that the FS of the slope decreases with the increase in \(\alpha_h\) values. This is because the increase in \(\alpha_h\) values promote the driving force to increase more. From Fig. 3 it is important to notice that when combined seismic loading is applied the slope reaches the failure condition much earlier as compared to the case of mono seismic loading. As an example, the slope was found stable (FS = 1.024) when only horizontal seismic acceleration with \(\alpha_h\) = 0.08 was applied, but by adding the vertical component (\(\alpha_v\) = 0.024) the slope was found unstable (FS = 1).

The variation of FS of the slope with a vertical seismic coefficient (\(\alpha_v\)) for different values of \({{c^{\prime}} / {\gamma H}}\) is depicted in Fig. 4 for \(\phi^{\prime} = 25^\circ\), \(\alpha_h = 0.1\). It was noticed that the sole application of horizontal seismic loading with \(\alpha_h\) = 0.1 gives a higher value of FS when the cohesion of the soil is high. On the other hand, with the introduction of \(\alpha_v\) conjunction with the application of \(\alpha_h\), the slope becomes unstable at the lower cohesion of the slope soil. Hence, the slope stability is greatly affected by the lower cohesion in the slope with application of combined seismic loading.

The factor of safety versus vertical seismic coefficient (\(\alpha_v\)) curve for various values of \(\phi^{\prime}\) is portrayed in Fig. 5. The variation was observed by keeping \({{c^{\prime}} / {\gamma H}} = 0.15\) and \(\alpha_h = 0.1\). From the plot, it was observed that the sole application of horizontal seismic loading with \(\alpha_h\) = 0.1 gives a higher value of FS when the friction angle of the soil is high. By introducing \(\alpha_v\) conjunction with the application of \(\alpha_h\), safety factor was reduced at the lower friction angle of the slope soil, but it did not fail. Hence, the slope stability is greatly influenced by the cohesion of the soil as compared to the friction angle.

Fig. 3.
figure 3

Factor of safety vs. horizontal seismic coefficient for different \(\alpha_v\).

Full size image
Fig. 4.
figure 4

Factor of safety vs. \(\alpha_v\) for various values of normalized cohesion.

Full size image

Figure 6 indicates the pattern of displacement vectors observed after applying a combined seismic loading with \(\alpha_h = 0.08\) and \(\alpha_v = 0.024\). It was found that the failure mass is moving outward down direction due to the combined action of seismic loads. The depth of the slip surface was approximately measured as 2m. From the results, it can be inferred that the slope which is estimated as stable by solely considering the horizontal component of the seismic loading may fail under the action of combined seismic loading.

Fig. 5.
figure 5

Factor of safety vs. \(\alpha_v\) for different values of friction angle.

Full size image
Fig. 6.
figure 6

Movement of failure mass due to combined seismic loading (\(\alpha_h = 0.08\), \(\alpha_v = 0.024\)).

Full size image

4 Analytical Solution for Pseudo-Static Analysis

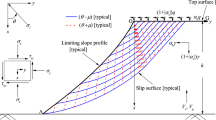
Figure 7 illustrates the rigid sliding block model which was used to calculate FS of the slope analytically based on the pseudo-static method. The rigid block starts sliding when the available shear resisting force is equal to the total driving force. In that situation, the block moves along the failure surface maintaining unaltered yield resistance [31]. The pseudo-static FS is calculated by resolving all the forces acting on the block at a particular instant of time based on limit equilibrium approach.

$$ FS = \frac{{{{c^{\prime}} / {\left( {\gamma z\cos \beta } \right) + \left[ {\left( {1 \pm \alpha_v } \right) - \alpha_h \tan \beta } \right]\tan \phi^{\prime}}}}}{{\left[ {\left( {1 \pm \alpha_v } \right)\tan \beta + \alpha_h } \right]}} $$
(5)

where \(z\) is the depth of the sliding block, approximated as 2 m after measuring the depth of the failure plane obtained from the numerical analysis (Fig. 6). The soil properties listed in Table 1 were used for inputs in the analytical expression of FS (Eq. 5). Finally, the FS of the slope was calculated by considering \(\alpha_h = 0.08\) and \(\alpha_v = 0.024\). The FS of the slope was found to be 0.75 which is on the lower side as compared to that obtained using finite-element-based pseudo-static analysis (FS = 1). This is because the limit-equilibrium-based pseudo-static stability is a simple method for seismic slope stability assessment which involves several simplified pressumptions associated with the shape of the slip surface and forces acting on them. However, both numerical and analytical analysis showed that the slope is unstable under combined seismic loading with \(\alpha_h = 0.08\) and \(\alpha_v = 0.024\) which signifies the validity of the present finite-element-based pseudo-static analysis.

Fig. 7.
figure 7

Sliding block model for pseudo-static stability analysis under combined seismic loads.

Full size image

5 Conclusions

In this study, an attempt was made to highlight the significance of vertical seismic acceleration in the stability analysis by performing a finite-element-based pseudo-static analysis under combined seismic loading condition. Also, a set of parametric studies were performed to demonstrate the impact of combined seismic loading on the slope stability with other soil parameters. Further, FS of the slope under combined seismic loading was calculated analytically on the basis of the rigid sliding block mechanism and compared with that computed using numerical analysis. Based on the results and discussion, the subsequent overall conclusions may be illustrated:

  • In the absence of vertical seismic acceleration, the slope was found unstable at \(\alpha_h\) = 0.1. This value of \(\alpha_h\) can be considered as the horizontal yield seismic coefficient of the slope. In this situation, a prominent slip surface developed throughout the slope face (from crest to toe). The maximum slope displacement under pseudo-static condition was computed as 4.42 mm.

  • The factor of safety versus \(\alpha_h\) curves for various values of vertical seismic coefficient showed that when combined seismic loading is applied the slope reaches the failure condition much earlier as compared to the case of sole seismic loading with the horizontal component.

  • The factor of safety versus \(\alpha_v\) curves for various values of normalized cohesion indicated that the slope stability was greatly influenced by the lower value of cohesion. Therefore, the impact of the vertical seismic coefficient on the FS is more evident by introducing the variation of soil cohesion. Also, it was detected that the stability of the present slope model highly depends on cohesion of soil as compared to friction angle.

  • The validity of the results computed using numerical analysis was established by comparing those with the stability result estimated analytically. However, the analytical expression gave a lower value of the FS due to the involvement of several simplified assumptions.