Overview of Incorporating Nonlinear Functions into Recurrent Neural Network Models

Abstract

This paper describes training recurrent neural networks (RNNs) which are able to learn features and long-range dependencies from sequential data. Although training RNNs is mostly plagued by the vanishing and exploding gradient problems, but there is a RNN architecture so called long short-term memory (LSTM) to address these issues. To demonstrate the impact of nonlinearity of activation functions on training recurrent neural networks, the limitations of the LSTM algorithm on speech recognition technology are presented in this study.

1 Introduction

Recurrent neural networks (RNNs) which have attracted great attention have been widely studied from 1986 and were based on David Rumelhart’s work for modeling time series. These networks are used for different machine learning tasks which can modelize sequential data.

Recurrent neural networks have many applications, especially when the input and output have variable lengths such as handwriting recognition, speech recognition, and image to text.

The layers of connected units called artificial neurons make artificial neural networks (ANNs). The shallow network of ANN includes an input layer, an output layer, and at most a hidden layer without a recurrent connection. Recurrent connections in ANNs make them recurrent neural networks (RNNs), and the increase of complexity of network depends on the number of layers. More number of layers or recurrent connections generally increases the depth of the network and empowers it to provide various levels of data representation and feature extraction, referred to as deep learning [1]. The difference between these networks and higher layer ones is related to their units. The structure of hidden states causes RNNs to store, remember, and process past complex signals for long time periods and works as the memory of the network and state of the hidden layer at a time which is conditioned on its previous state [2]. Mapping the input sequence at the current timestep to the output sequence which is prediction the sequence in the next timestep is the another capability of RNNs. Artificial neurons and the feedback loops which are recurrent cycles over time or sequence make RNNs as a class of supervised machine learning models [3]. In this model, for training the RNNs, the dataset of input-target pairs needs to be trained, and the goal is minimizing the difference between output and target pairs via optimizing the weights of the network. This work is based on training recurrent neural network [1] and error bound for approximations [4].

Definition 1.1

(Neural Network) Let $d,L \in \mathbb {N}$. A neural network U with input dimension d and L layers is a sequence of matrix-vector tuples

$$\begin{aligned} U=\left( (A_1,b_1),(A_2,b_2),\ldots ,(A_L,b_L)\right) \end{aligned}$$

where $N_0=d$ and $N_1,\ldots ,N_L \in \mathbb {N}$ and where

$$\begin{aligned} A_L:=N_L \times \sum \limits _{k=0}^{L-1}N_K, \end{aligned}$$

and $b_L \in \mathbb {R}^{N_L}.$ (Note that $N_L$ is the definition of the output layer of U)

2 A Simple Recurrent Neural Network

Recurrent cycles over time are called feedback loops. In the neural network literature, artificial neurons with one or more global feedback are referred to as recurrent networks [1]. RNNs are a class of supervised machine learning models. Learning capability of the RNNs and its performance depends on the amount of feedback loops.

Also where the output of a neuron is fed back into its own input, the network has self-feedback. Moreover in the situation that neural network contains nonlinear units, feedback loops include particular branches unit time delay operators (denoted by $Z^{-1}$ in the figure).

2.1 Model Architecture

Recurrent neural network architectures can have many different forms. The layer of input, recurrent hidden, and layer of output are three layers in simple RNNs.

A sequence of vectors through time $\{\ldots ,x_{t-1},x_t,x_{t+1},\ldots \}$ such that $x_t=\{x_1,x_2,\ldots ,x_N\}$ makes the input of input layer.

In a fully connected RNN, the input units are connected to the hidden units. In this layer, a weight matrix $W_{\text {IH}}$ defines the connections. The hidden units $h_t=\{h_1,h_2,\ldots ,h_N\}$ cause the hidden layer to connect with recurrent connections through time. The stability and performance of the network depend on the initialization of the hidden units with small elements. The state space (memory) of the system is defined by hidden layer as

$$\begin{aligned} h_t=f_{\text {H}}(O_t) \end{aligned}$$

(2.1)

such that $f_{\text {H}}(.)$ is the activation function and

$$\begin{aligned} O_t=W_{\text {IH}}x_t+W_{\text {HH}}h_{t-1}+b_{\text {h}} \end{aligned}$$

In the hidden units, $b_{\text {h}}$ is the bias vector. In the third layer which is output layer, the units are computed as

$$\begin{aligned} y _t=f_{\text {O}}(W_{\text {HO}}h_t+b_0) \end{aligned}$$

where $f_{\text {O}}(.)$ is activation function and $b_0$ is the bias in this layer. Weighted connections $W_{\text {HO}}$ connect the hidden layer to the output layer. A set of values which summarizes all the unique necessary information of the previous states of the network through the time is hidden state of a RNN. These hidden states make accurate predictions at the output layer according to input vector. If a simple RNN is trained well, the network will be capable for modeling rich dynamics; however in every units, simple activation function is used [1].

2.2 Activation Function

In the output layer for training a classification model, an activation function is applied. The activation function must be continuous in order to meet differentiability requirements. Sigmoidal nonlinear functions are examples of a continuously differentiable nonlinear activation functions which are used in multi-layer perceptrons.

Some popular activation functions are rectified linear unit (ReLU) , “$\tanh$”, and “sigmoid”. These functions (“tanh” and “sigmoid”) are two forms of sigmoidal nonlinear functions.

Both the nature of the machine learning problem and the training dataset are two important factors for choosing the proper activation function. The activation function typically takes the form of a hyperbolic tangent function which is defined as

$$\begin{aligned} \tanh (x)=\frac{{\text {e}}^{2x}-1}{{\text {e}}^{2x}+1} \end{aligned}$$

or logistic(sigmoid) function which is known as common choice activation function

$$\begin{aligned} \sigma (x)=\frac{1}{1+{\text {e}}^{-x}} \end{aligned}$$

The domain of this function is real numbers, and its range is [0, 1]. These two activation functions which fastly saturate the neuron and cause the gradient to be vanished are related as

$$\begin{aligned} \sigma (x)=\frac{\tanh \left( \frac{x}{2}\right) +1}{2} \end{aligned}$$

Obviously, the scaled version of sigmoid activation function is $\tanh$. The ReLU activation function which works on positive input values is defined as

$$\begin{aligned} \rho (x)=\max (x,0) \end{aligned}$$

Although comparison between ReLU activation function and another two activation functions indicates that in ReLU activation function, the acceleration of the convergence of stochastic gradient descent (SGD) is greater than tanh and sigmoid, but due to the lack of resistance of ReLU function against growing the weight matrix and the large gradient, neuron may be inactive by using of this type of activation function during training.

3 Training Recurrent Neural Network

Training the RNN in which the training loss being minimized is a main issue in such networks. Optimizing the algorithm in order to tune the weights and instantiating them are the main approaches used for minimizing the training loss. The main focus in optimizing the machine learning algorithm is on the convergence and reducing the complexity of training section of the algorithm which needs a large number of iterations. There are many approaches for training RNNs. In this paper, we study activation functions in gradient-based machine learning algorithms and their modified forms.

3.1 Gradient-Based Learning Methods

One of the most common approaches to optimize neural network is gradient descent (GD). Although this method causes the total loss to minimized, but for large datasets, this method is computationally expensive and is not appropriate for training the models as inputs arrive (i.e., online training). Basically in this way by computing the error function derivative with respect to each member of the weight matrices, the weights of the model are set. Assuming that the activation function is nonlinear and differentiable, in order to minimize the total loss, the gradient descent alters at each weight. In GD, each iteration of optimization for doing an update follows of this formula:

$$\begin{aligned} \theta _{t+1}=\theta _t-\frac{\lambda }{U}\sum _{k=1}^{U}\frac{\partial L_k}{\partial \theta } \end{aligned}$$

where $\lambda$ is the rate of training and U is the extent of training set and $\theta$ is the set of parameters. The gradient for whole dataset is computed by GD so GD is considered as batch GD. In other words, by GD method, we follow the direction of the slope of the surface created by the objective function downhill until we reach a valley [5]. Since the time is not considered in GD and RNNs include recurrent cycles over time, so this method does not work properly for training the network. For solving this problem, an extended version of GD through time is needed. It is called backpropagation through time (BPTT). Basically, backpropagation is a specific technique for implementing gradient descent in the weight space for a multi-layer perception [6]. In RNN, the connections between parameters and the dynamics are unstable, this makes computing error-derivatives through time complicated, and GD method is thus inadequate. Another shortcoming of GD is due to the difficulty in recognizing the dependencies as they increase in magnitude. The only parameter which is considered by loss function derivative with respect to weights is the distance between the updated output and its consistent target as the history of weights information is not applied. The vanishing gradient is another deficiency of applying GD method for training RNN. The exponential decay of backpropagated gradient causes RNNs not to learn long-term temporal dependencies. In a reverse situation, GD method may lead to explode gradient issue which is due to exponentially blow-up of backpropagated gradient. This result is in unstable learning process. We are going to discuss these challenges and provide an architecture for solving these problems.

3.1.1 Backpropagation Through Time (BPTT)

The simplest type of neural network is the feedforward neural network. This network has no loop, and the information moves from input nodes, via hidden ones and finally output nodes (i.e., in only one direction). For feedforward networks, the method “BPTT” is used to train the network. BPTT is the generalization of backpropagation. In this method, the idea is making the network unfolded in time, and the signals of error propagate backwards through time [2].

In this network, the parameters can be considered as the set

$$\begin{aligned} \theta =\{W_{\text {HH}},W_{\text {IH}},W_{\text {HO}},b_{\text {h}},b_{\text {I}},b_{\text {O}}\} \end{aligned}$$

(3.1)

These parameters affect the loss function in the previous timesteps. The gradients of loss function with respect to this set are

$$\begin{aligned} \frac{\partial L}{\partial \theta }=\sum _{t=1}^{T}\frac{\partial L_T}{\partial \theta } \end{aligned}$$

where for the loss function L, we have

$$\begin{aligned} \frac{\partial L_t}{\partial \theta }=\sum _{k=1}^{t}\left( \frac{\partial L_t}{\partial h_t}.\frac{\partial h_t}{\partial h_k}.\frac{\partial {h_k^+}}{\partial \theta }\right) , \end{aligned}$$

where $h_t$ is the hidden state of network at time t and $\frac{\partial {h_k^+}}{\partial \theta }$ is the “immediate” partial derivative. For propagating the error signals backward in timestpes t and k which is $k<t$, we have

$$\begin{aligned} \frac{\partial h_t}{\partial h_k}=\prod _{i=k+1}^t \frac{\partial h_i}{\partial h_{i-1} }, \end{aligned}$$

and so according to Eq. (2.1) and using the Jacobian matrix for the hidden state we have:

$$\begin{aligned} \prod _{i=k+1}^t \frac{\partial h_i}{\partial h_{i-1}} =\prod _{i=k+1}^t W_{\text {HH}}^{T} {\text {diag}} |f'_{\text {H}} (h_{i-1})|. \end{aligned}$$

As we see the participation of the hidden states in the network through time is obvious. In terms of the contribution of inputs and corresponding hidden states over time, two types of hidden state contribution are recognizable, such as long-term contribution (for time $k \ll t$ ) and short time contribution for another time.

By considering the above figure, it is evident that when the new input are admitted to the network, the sensitivity of units vanishes (decreasing the contribution of the inputs $x_{t-1}$ through time), the activation in hidden units is overwritten by BPTT (increasing the contribution of the loss function value $L_{t+1}$ w.r.t $h_{t+1}$ in BPTT trough time) [1].

3.1.2 Vanishing Gradient Problem

The vanishing gradient problem causes some defects for RNNs. This is because of strong nonlinearity which is used for making complex pattern of data. When the gradient propagates back through time, its magnitude decreases exponentially. Subsequently, the long-term correlations are neglected by the network, which causes an issue in learning process of dependencies among distant events. There are two possible explanations for this:

• 1. The gradient of nonlinear functions which is close to zero.

• 2. While the gradient propagates back through time, recurrent matrix increases the gradient magnitude.

For the less than one eigenvalues of the recurrent matrix, after five to ten times of running backpropagation algorithm, the rate of convergence of gradient increases. In the RNNs learning process with extended sequences and small weights, the gradient shrinks as well. Long-term components explode in the recurrent weight matrix $W_{\text {HH}}$ when its spectral radius becomes more than 1 and $t \rightarrow \infty$ . Because product of matrices can lead to shrinkage/explosion along several directions. In order to generalize this to nonlinear function $f'_h(.)$ in Eq. (2.1), we can bound it with $\gamma \in \mathbb {R}$ s.t

$$\begin{aligned} \Vert {\text {diag}}(f'_H(h_k))\Vert \le \gamma \end{aligned}$$

And since we have

$$\begin{aligned} \displaystyle \prod _{i=k+1}^t \frac{\partial h_i}{\partial h_{i-1}} =\prod _{i=k+1}^t W_{\text {HH}}^{T} {\text {diag}} |f'_{\text {H}} (h_{i-1})| \end{aligned}$$

so

$$\begin{aligned} \left\| \frac{\partial h_{k+1}}{\partial h_{k}}\right\| \le \left\| W_{\text {HH}}^T\right\| .\left\| {\text {diag}}(f''_{\text {H}} (h_{k}))\right\| \le 1 \end{aligned}$$

Now for $\delta \in \mathbb {R}$, if we consider $\Vert \frac{\partial h_{k+1}}{\partial h_{k}}\Vert \le \delta <1$ for loss function component, we have

$$\begin{aligned} \left\| \frac{\partial L_t}{\partial h_{t}}\left( \prod _{i=1}^{t-1} \frac{\partial h_{i+1}}{\partial h_{i}}\right) \right\| \le \delta ^{t-k} \Vert \frac{\partial L_t}{\partial h_t}\Vert \end{aligned}$$

in different timesteps. Since $\delta < 1$, increasing $t-k$ leads to vanishing gradient problem. Generally in recurrent matrix $W_{\text {HH}}$, if for the largest singular value $\lambda _1$ we have $\lambda _1 <\frac{1}{\gamma }$, the gradient vanishing problem happens.

3.1.3 Exploding Gradient Problem

As its mentioned, the process of training RNNs with BPTT may be exposed by exploding problem. In training recurrent neural networks on long sequences, increasing the weights causes the norm of gradient to increase and gradients are subsequently exploded. This is a different necessary condition in comparison to the vanishing gradient problem in which for the largest singular value of recurrent matrix $W_{\text {HH}}$ (i.e., $\lambda _1$), we have $\lambda _1 >{\frac{1}{\gamma }}$.

4 Long Short-term Memory

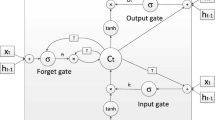
As mentioned before, the main shortcoming of BPTT method pertains to error signals flowing backwards in time. This causes gradients to vanish or explode through time which turns out to more difficulties in learning long-term dependencies. To tackle this problem, some methods have been proposed. One of the most successful techniques to strengthen the long-term dependencies is known to be the long short-term memory (LSTM). In this method, the sigmoid or tanh hidden units are replaced with “memory cell”. This change leads to more controlled behavior of backpropagated gradients. In this approach, the input and output values of the cell memory are controlled by gates. Each cell is also matched with a forget gate that controls the decay rate of its stored values [7]. In this way, the memory cell holds its stored values during the periods that the input and output gates are off, and the forget gate is not causing decay [1]. Therefore, the gradient of the error with respect to its stored value, when backpropagated over those periods, stays constant [8]. Depending on the training application, there are varieties of LSTM structures developed by many researchers. In the following chapter, standard LSTM approach will be illustrated, and then, we will focus on bidirectional LSTM in particular to suit our applications.

4.1 Standard LSTM

As its shown in above figure, each typical memory cell has its own input, output, and forget gate and a cell activation component that provide continuous analogs of write, read, and reset operations for the cells. More precisely, the input, forget, and output gate are trainable to learn, respectively, what information to store in the memory, how long to store it, and when to read it out [9]. The activation of the cell is controlled by the designed multipliers. The input to the cells is multiplied by the activation of the input gate, the output to the net is multiplied by that of the output gate, and the previous cell values are multiplied by the forget gate. The net can only interact with the cells via the gates [10]. The input gate of LSTM is defined as

$$\begin{aligned} g_t^{\text {in}}=\sigma (W_{{\text {Ig}}^{{\text {in}}}}x_t+W_{{\text {Hg}}^{{\text {in}}}}h_{t-1}+W_{{\text {g}}^{\text {c}}\mathrm{{g}}^{{\text {in}}}}g_{t-1}^{\text {c}}+b_{{\text {g}}^{{\text {in}}}}) \end{aligned}$$

(4.1)

where $W_{\ldots }$ is the weight matrix as below

• $W_{{\text {Ig}}^{{\text {in}}}}$: $\text {input layer}\rightarrow \text {input gate}$

• $W_{{\text {Hg}}^{{\text {in}}}}$ : $\text {hidden state}\rightarrow \text {input gate}$

• $W_{{\text {g}}^{\text {c}}\mathrm{{g}}^{{\text {in}}}}$: $\text {cell activation}\rightarrow \text {input gate}$

• $b_{{\text {g}}^{{\text {in}}}}$ : bias of the input gate

• forget gate :

  $$\begin{aligned} g_t^{{\text {f}}}=\sigma (W_{{\text {Ig}}^{\text {f}}}x_t+W_{{\text {Hg}}^{\text {f}}}h_{t-1}+W_{{\text {g}}^{\text {c}}\mathrm{{g}}^f}g_{t-1}^{\text {c}}+b_{{\text {g}}^{\text {f}}}) \end{aligned}$$

  (4.2)

where

• $W_{{\text {Ig}}^{\text {f}}}$: $\text {input layer}\rightarrow \text {forget gate}$

• $W_{{\text {Hg}}^{\text {f}}}$ : $\text {hidden state}\rightarrow \text {forget gate}$

• $W_{{\text {g}}^{\text {c}}\mathrm{{g}}^{\text {f}}}$: $\text {cell activation}\rightarrow \text {forget gate}$

• $b_{{\text {g}}^{\text {f}}}$ : bias of the forget gate

• cell gate:

  $$\begin{aligned} g_t^{{\text {c}}}=g_t^{{\text {in}}} {\text {tan}}h (W_{{\text {Ig}}^{{\text {c}}}}x_t+W_{{\text {Hg}}^{{\text {c}}}}h_{t-1}+b_{{\text {g}}^{c}})+g_t^{{\text {f}}}g_{t-1}^{{\text {c}}} \end{aligned}$$

  (4.3)

where

• $W_{{\text {Ig}}^{{\text {c}}}}$: $\text {input layer}\rightarrow \text {cell gate}$

• $W_{{\text {Hg}}^{{\text {c}}}}$ : $\text {hidden state}\rightarrow \text {cell gate}$

• $b_{{\text {g}}^{\text {c}}}$ : bias of the cell gate

• output gate:

  $$\begin{aligned} g_t^{{\text {out}}}=\sigma (W_{{\text {Ig}}^{{\text {out}}}}x_t+W_{{\text {Hg}}^{{\text {out}}}}h_{t-1}+W_{{\text {g}}^{\text {c}}\mathrm{{g}}^{{\text {out}}}}g_{t}^{\text {c}}+b_{{\text {g}}^{{\text {out}}}}) \end{aligned}$$

  (4.4)

where

• $W_{{\text {Ig}}^{{\text {out}}}}$: $\text {input layer}\rightarrow \text {output gate}$

• $W_{{\text {Hg}}^{{\text {out}}}}$ : $\text {hidden state}\rightarrow \text {output gate}$

• $W_{{\text {g}}^{\text {c}}\mathrm{{g}}^{{\text {out}}}}$: $\text {cell activation}\rightarrow \text {output gate}$

• $b_{{\text {g}}^{{\text {out}}}}$ : bias of the output gate

• hidden state:

  $$\begin{aligned} h_t=g_t^{{\text {out}}} {\text {tan}}h(g_t^{\text {c}}) \end{aligned}$$

  (4.5)

The LSTM gates can prevent the rest of the network from modifying the contents of the memory cells for multiple timesteps [1].

4.2 Bidirectional LSTM

In order to train data, looking at the previous context and future context is important and has many applications such as speech recognition Bidirectional RNN (BRNN) considers all available input sequence in both the past and future for estimation of the output vector [11]. To enhance the capability of BRNNs through stacking hidden layers of LSTM cells in space, deep bidirectional LSTM (BLSTM) can be applied. BLSTM networks are more powerful than unidirectional LSTM networks [1]. This means that the bidirectional nets and the LSTM nets did not take significantly more time to train per epoch than the unidirectional or RNN [10]. During computation, BLSTM includes all information of input sequences. Like BRNN, BLSTM model can solve the vanishing gradient problem and extend the model. But biggest difference between BRNN and BLSTM is related to their training time. The convergence of BRNN is more than eight times as long respect to BLSTM.

We consider an extended LSTM layer in multi-layer net, and the pseudocode for the forward pass is described.

4.2.1 Notation

• S input sequence

• $\tau$ time

• $x_{k}(\tau )$ network input to unit k at the time $\tau$

• $y_k (\tau )$ the activation of the network input

• $E(\tau )$ output error at the time $\tau$

• $t_{k} (\tau )$ training target at output unit k at time $\tau$

• N set of all units (input units, bias units)

• $W_{ij}$ weight from unit i to unit j

• $\iota$ input gate

• $\phi$ forget gate

• $\omega$ output gate

• c elements of the set of cells C

• $s_{{c}}$ state value of cell c

• f is a function of gate

• g cell input function

• h output function

Note that for each memory block, the LSTM equations are written, and these calculations can be repeated for each block. The error gradient is calculated with online BPTT, i.e., after every sequence BPTT shrink to input sequence length with the weight updates [10].

4.2.2 Forward Pass

• Re-adapt the activation to 0,

• Feed in the inputs and update the activation functions. All hidden layer and output activation functions at every timestep need to be stored,

• The activation functions are updated as: Input Gates

  $$\begin{aligned} x_t=\displaystyle \sum _{j \in N} \omega _{\iota j}y_j (\tau -1)+\sum _{c \in C}\omega _{\iota c}s_c (\tau -1) \end{aligned}$$
  $$\begin{aligned} y_{\iota }=f(x_{\iota }) \end{aligned}$$

  Forget Gates

  $$\begin{aligned} x_\phi =\sum _{j \in N} \omega _{\phi j}y_j (\tau -1)+\sum _{c \in C}\omega _{\phi c}s_c (\tau -1) \end{aligned}$$

5 Application of LSTM in Speech Recognition

5.1 Speech Recognition

Since RNNs are the structure through time and the signals of speech and audio change continuously over time, so RNNs can be an ideal model to learn features. Also speech recognition prediction uses the past and future sequential data, so BRNN is suitable in this field. Later applications of the connectionist temporal classification (CTC) function contributed to promote the RNNs in speech recognition. Connectionist temporal classification (CTC) is an objective function that allows an RNN to be trained for sequence transcription tasks without requiring any prior alignment between the input and target sequences [12]. CTC model has iterations like the sequence transducer and neural transducer. This property enables a second RNN to perform as a language model. This eventually leads to do the task such as online speech recognition. So by these argumentation, based on linguistic feature and prior transcriptions, the model can make the prediction.

5.2 Speech Emotion

Another application of RNNs is speech emotion. In this field, the segment of speech is organized as an emotion. Since in speech emotion recognition, the progress proceeds from the same way as that of speech recognition so the speech emotion recognition is much the same to speech recognition. Several methods have been proposed in speech application such as hidden Markov model (HMMs) and Gaussian mixture models (GMMs). With RNNs establishment, the trend of learning has improved. Because the networks were able to learn the features on their own. So RNN models have been applied for performing speech emotion recognition. LSTM–RNN has been successfully applied to speech recognition. Because in LSTM network, long-range dependencies are modelized better in order to capture the emotions. Also deep bidirectional LSTMs can capture more data through taking them in large number of frames.

5.3 Speech Synthetic

Another type of speech application is speech synthetic. In this field, long-term sequence learning is needed as well. HMM-based models and deep MLP neural networks can synthesize speech. However, these models have some problems. For example, in HMM-based models, statistical averaging during the training phase leads to overly smooth trajectories so the sound is not natural or MLP neural network takes each frame as an independent entity from its neighbors and fails to take into account the sequential nature of speech [13]. Introducing the RNNs in speech synthesis collaborates to leverage the sequential dependencies.

Speech synthesis also requires long-term sequence learning. HMM-based models can often produce synthesized speech, which does not sound natural. This is due to the overly smooth trajectories produced by the model, as a result of statistical averaging during the training phase [13].

Following that, LSTM performs better than RNNs. Also the ability of BLSTM model to integrate the relationship with neighboring frames in both future and past time steps [14, 15] make this model very effective in learning long-term sequential dependencies.