Predictive Control Techniques for Induction Motor Drive for Industrial Applications

Abstract

In this paper, three popular model predictive control (MPC) techniques, namely predictive current control (PCC), predictive torque control (PTC), and predictive flux control (PFC), applied to induction motor (IM) drive are presented. These techniques directly use the inherent discrete nature of the power converter and evaluate control parameters for the finite switching states. These control techniques for IM can offer fast dynamic response, improved steady-state operation, and retain the decoupled nature. In case of PTC, weighting factor is used in cost function, whereas in other two control techniques, weighting factor is only required when additional control parameters are added. These control techniques are developed in MATLAB/SIMULINK, and results are presented for various operating conditions.

1 Introduction

The induction motors are essentially used in industrial applications for variable speed drives owing to its rugged construction, reliable, and maintenance free operation. In some of the industrial applications, it is necessary to maintain quick dynamic response and also minimal torque ripple. In order to ensure the fast dynamic response, decoupling of control parameter (i.e., torque and flux) is essential. The decoupled control can be obtained by using well-established vector control or direct torque control (DTC). To overcome existing drawbacks in vector control and DTC in industrial drives, MPC techniques have been proposed [1,2,3,4,5,6].

This paper presents three popular MPC techniques used for IM drive. The first idea about applying MPC to power electronics was started in the1980s. MPC is most used recent methods for power converter and drive applications. Among the different techniques of MPC applied for IM drive: PCC, PTC, and PFC become more attractive. The PCC technique for IM drive was presented in [1, 2]. In this control technique, stator currents are measured as control parameters, and those parameters are used for required prediction and cost function optimization. This control technique is similar to FOC implementation for an IM drive. In the PTC technique, initially, the ψ_s is estimated followed by prediction of T and ψ and cost function optimization [3,4,5]. To maintain appropriate balance among ψ and T, weighting factor can be used. However, additional adjustment of weighting factor is necessary in the real-time implementation. The structure of PTC is similar to DTC for an IM drive. The major drawback of PTC is tuning of the weighting factor in the cost function. To overcome this problem, PFC is presented in [6]. In PFC, instantaneous control of T and ψ is replaced by ψ_s control alone. Hence, weighting factor can be eliminated in cost function. From all the various PCC, PTC, and PFC, control techniques are reported in [7,8,9,10,11,12,13,14,15].

This paper presented as IM model and VSI model is presented in Sect. 2. Three popular MPC techniques, namely PCC, PTC, and PFC, for an IM drive are given in Sect. 3. Sections 4 and 5: Results and conclusions are described, respectively.

2 Modeling of IM and VSI

The IM is used for implementation of PCC, PTC, and PFC techniques. The general steps used for the execution of these control techniques for the IM drive are estimations, predictions, and cost function optimization. The dynamic model of an IM can be represented as [1].

$$ \nu_s = R_s i_s + {{({\text{d}}} / {{\text{d}}t}})\psi_s $$

(1)

$$ 0 = R_r i_r + ({{\text{d}} / {{\text{d}}t)}}\psi_r - j\omega \psi_r $$

(2)

$$ \psi_s = L_s i_s + L_m i_r $$

(3)

$$ \psi_r = L_r i_r + L_m i_s $$

(4)

$$ {\rm T} = ({3 / 2})p(\psi_s^* \otimes i_s ) $$

(5)

$$ {{({\text{d}}} / {{\text{d}}t}})\omega = {{(1} / J})\left( {T - T_l } \right) $$

(6)

The required dynamic model of the 2-level VSI is presented here. All the feasible voltage vectors and related switching states are presented in Fig. 1. Different switching states of the voltage vectors are given as

$$ S = ({2 / {3)}}\left( {S_a + aS_b + a^2 S_c } \right) $$

(7)

Fig. 1

Voltage vector diagram of 2-level inverter

where a = e^j2π/3 and S_i = 1 represent upper switch of associated phase is ON and S_i = 0 represents upper switch of associated phase is in OFF condition. Here, i = a, b, c (phases).

The output voltage vector can be represented by

$$ v = V_{{\text{dc}}} S $$

(8)

where V_dc = DC-link voltage.

The above dynamic model of IM and VSI is used to implement the three predictive control techniques.

3 Model Predictive Control Techniques for an IM Drive

The concept of MPC refers to a controller that uses the model of system to select an optimal control action. Here, all the three MPC techniques for an IM drive are presented in a detailed manner.

3.1 PCC

The control structure of PCC technique is represented in Fig. 2.

Fig. 2

PCC for an IM drive

Initially, stator currents are measured and converted into stationary reference frame. The predicted stator currents are used for all possible voltage vectors in the following sampling period. These predictions are used to define a cost function.

Therefore, cost function can be evaluated for all the switching states of the 2-level VSI. From dynamic model of IM described in above, i_s can be represented as

$$ i_s = - ({1 / {R_\sigma }})\left( {\left( {L_\sigma ({{\text{d}} / {{\text{d}}t}})i_s - k_r \left( {({1 / {T_r }}) - j\omega } \right)\psi_r } \right) - v_s } \right) $$

(9)

where k_r = L_m/L_r, R_σ = R_s + k_r²R_r and L_σ = σL_s.

The i_s can be predicted in next time step.

$$ {{({\text{d}}} / {{\text{d}}t}})x = {{(x(k + 1) - x(k))} / {T_{\text{s}} }} $$

(10)

where T_s denotes sampling period. From Eqs. (9) and (10), the predicted i_s is given as

$$ i_s (k + 1) = \left( {1 - ({{T_{\text{s}} } / {\tau_\sigma )}}} \right)i_s \left( k \right) + ({{T_{\text{s}} } / {\tau_\sigma )}}({1 / {R_\sigma }})\left[ {k_r \left( {({1 / {T_r }}) - j\omega \left( k \right)} \right)\psi_r \left( k \right) + v_s \left( k \right)} \right] $$

(11)

where τ_σ = σL_s/R_σ.

The cost function is represented by

$$ G_j = \sum_{h = 1}^N {\left\{ {\left| {i_\alpha^* - i_\alpha (k + h)_j } \right| + \left| {i_\beta^* - i_\beta (k + h)_j } \right|} \right\}} $$

(12)

where j = 0 to 6 are the switching states of the 2-level VSI.

To realize the PCC technique, generation of the reference currents is required. The outer PI controller generates T reference, and ψ_r reference is rated value. From these reference values, $i_d^*$ and $i_q^*$ are generated as

$$ i_d^* = ({{\left| {\psi_r } \right|^* } / {L_m }}) $$

(13)

$$ i_q^* = ({2 / 3})({{L_r } / {L_m }})({{T^* } / {\left| {\psi_r } \right|^* }}) $$

(14)

The reference current generation is similar to classical FOC. However, the PI controller along with modulation stage is replaced with MPC technique.

3.2 PTC

The control structure of the PTC technique is represented in Fig. 3. In this control technique, estimation of ψ_s, prediction of control parameters, and optimization of cost function are the main aspects.

Fig. 3

PTC for an IM drive

The required predictions of the control technique will be obtained by using Eqs. (1)–(4) and Eq. (11) as follows:

$$ \psi_s \left( {k + 1} \right) = \psi_s \left( k \right) + T_{\text{s}} v_s \left( k \right) - R_s T_{\text{s}} i_s \left( k \right) $$

(15)

$$ \begin{aligned} i_s (k + 1) & = \left( {1 - ({{T_{\text{s}} } / {\tau _\sigma )}}} \right)i_s \left( k \right) + ({{T_{\text{s}} } / {\tau _\sigma )}}({1 / {R_\sigma }})\left[ {k_r \left( {({1 / {T_r }}) - j\omega \left( k \right)} \right)\psi _r \left( k \right)} \right. \\ & \quad \left. { + v_s \left( k \right)} \right] \\ \end{aligned} $$

(16)

From the Eqs. (5), (15), and (16), the T is given as

$$ T\left( {k + 1} \right) = ({3 / 2})p\left[ {\psi_s \left( {k + 1} \right) \otimes i_s \left( {k + 1} \right)} \right] $$

(17)

Finally, the required cost function can be obtained as

$$ G_j = \sum_{h = 1}^N {\left\{ {\left| {T^* - T\left( {k + h} \right)_j } \right| + \lambda \left| {\left\| {\psi_s^* } \right\| - \left\| {\psi_s \left( {k + h} \right)_j } \right\|} \right|} \right\}} $$

(18)

where λ is the weighing factor used to provide relative balance between T and ψ in cost function optimization. This weighing factor has to be adjusted to get the satisfactory operating conditions. The control structure of PTC is similar to DTC, whereas hysteresis controller and switching table are replaced with MPC technique.

3.3 PFC

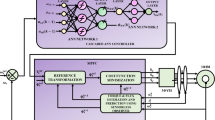
To overcome the weighting factor problem in PTC, PFC was introduced in [6]. The block diagram of IM drive with PFC is shown in Fig. 4. The PFC technique also involves in estimation and prediction of control parameters and cost function optimization. From above mathematical model of IM, ψ_s and ψ_r for the current sampling instant (k) are given as

$$ \psi_s \left( k \right) = \psi_s \left( {k - 1} \right) + T_{\text{s}} \left[ {v_s \left( {k - 1} \right) - R_s i_s \left( {k - 1} \right)} \right] $$

(19)

$$ \psi_r \left( k \right) = \left( {L_r /L_m } \right)\psi_s \left( k \right) - \left( {1/\lambda L_m } \right)i_s \left( {k - 1} \right) $$

(20)

Fig. 4

PFC of an IM drive

Based on the estimated values, i_s, ψ_s, and ψ_r can be predicted as follows:

$$ \psi_s \left( {k + 1} \right) = \psi_s \left( k \right) + T_{\text{s}} \left[ {v_s \left( k \right) - R_s i_s \left( k \right)} \right] $$

(21)

$$ \begin{aligned} i_s \left( {k + 1} \right) & = i_s \left( k \right) + T_{\text{s}} \left\{ {\lambda \left( {R_r - jL_r \omega _r } \right)\psi _s \left( k \right) - \left[ {\lambda \left( {R_s L_r + R_r L_s } \right) + j\omega _r } \right]i_s \left( k \right)} \right. \\ & \quad \left. { + \lambda L_r \left( {v_s \left( k \right)} \right)} \right\} \\ \end{aligned} $$

(22)

$$ \psi_r \left( {k + 1} \right) = \psi_r \left( k \right) + T_{\text{s}} \left\{ {R_r \left( {L_m /L_r } \right)i_s \left( k \right) - \left[ {\left( {R_r /L_r } \right) - j\omega_r } \right]\psi_r (k)} \right\} $$

(23)

The magnitude of reference ψ_s can be selected as follows:

$$ \left| {\psi_s^{ref} } \right| = \left| {\psi_s^* } \right| $$

(24)

The T can be expressed as

$$ T = {{(3} / {2)}}p\lambda_\sigma L_m \left( {\psi_r \otimes \psi_s } \right) $$

(25)

where $\lambda_\sigma = {1 / {\left( {L_s .L_r - L_m^2 } \right)}}$.

By using Eqs. (24) and (25), the following relation should be satisfied

$$ T = ({3 / 2})p\lambda_\sigma L_m \left( {\psi_r \otimes \psi_s^{{\text{ref}}} } \right) $$

(26)

Now, the reference ψ_s can be represented as

$$ \psi_s^{{\text{ref}}} = \psi_s^* \exp \left( {j\angle \psi_s^{{\text{ref}}} } \right) $$

(27)

$$ \angle \psi_s^{{\text{ref}}} = \angle \psi_r + \arcsin \left( {T^* /1.5p\lambda_\sigma L_m \left| {\psi_r } \right|\left| {\psi_s^* } \right|} \right) $$

(28)

From Eqs. (21) and (27), the cost function is given as

$$ G = \left| {\psi_s^{{\text{ref}}} - \psi_s \left( {k + 1} \right)} \right| $$

(29)

By optimizing the above cost function, suitable optimal voltage will be chosen for next step. Weighting factor is not necessary in cost function due to the single control parameter.

4 Results

The simulation results for PCC, PTC, and PFC are presented in MATLAB/SIMULINK for a sampling period is 50 µsec. To results are shown for steady-state operation with different speeds and dynamic load response and speed reversal. In each result, graphs are shown for ω, i_s, and T.

The steady-state operation of IM drive with ω₁ = 50 rad/sec, ω₂ = 100 rad/sec, and ω₃ = 150 rad/sec with T_l = 10 N-m for all the three control techniques is shown in Figs. 5, 6 and 7, respectively. It is evident from the above results, PFC is offering better T response. However, by adjusting the weighting factor in PTC, T ripple can be minimized with increased deviations in ψ_s. In Fig. 8, similar dynamic response of the drive can be observed with the sudden change in load from 0 to 10 N-m at t = 2 s. The speed reversal of IM drive from 150 to −150 rad/sec is shown in Fig. 9. Similar response can be observed in all these techniques.

Fig. 5

ω, i_s, and T waveforms of an IM drive with low speed (50 rad/sec) in steady-state operation a PCC, b PTC, c PFC

Fig. 6

ω, i_s, and T waveforms of an IM drive with medium speed (100 rad/sec) in steady-state operation a PCC, b PTC, c PFC

Fig. 7

ω, i_s, and T waveforms of an IM drive with rated speed in steady-state operation a PCC, b PTC, c PFC

Fig. 8

ω, i_s, and T waveforms of an IM drive with 150 rad/sec rated speed and 10 N-m load torque a PCC, b PTC, c PFC

Fig. 9

ω, i_s, and T waveforms of an IM drive for speed reversal operation a PCC, b PTC, c PFC

5 Conclusion

The basic ideas of various model predictive methods are used for IM drive in industrial applications. An attempt is made to present the implementation of PCC, PTC, and PFC for an IM drive. Results are presented for both steady-state and dynamic operating conditions for these three methods. The major advantages of these methods are easy to understand, and direct inclusion of control objectives is possible in the cost function.