Integral Reinforcement Learning-Based $H_\infty$ Tracking Control for Uncertain Linear Systems and Its Application

Abstract

In this paper, a robust optimal tracking strategy is presented for linear system with systems uncertainty and bounded disturbance. Firstly, an integral sliding mode control policy is designed to guarantee system trajectories tend to a defined sliding mode surface and the influence of system uncertainty is eliminated. Then the robust tracking control problem of original system is transformed into the $H_\infty$ control problem of an auxiliary error system. Furthermore, an off-policy integral reinforcement learning (IRL) algorithm based $H_\infty$ controller is designed, where the optimal tracking performance is guaranteed under the adverse effect of external disturbance. Finally, simulation test for near space vehicle (NSV) attitude model is introduced to verify the effectiveness of the proposed strategy.

1 Introduction

Nowadays, the robust control method has received considerable attention from industrial and academic areas [1]. As far as we know, there are many effective methods to deal with the uncertainty. Such as disturbance observer-based (DO) control [2] and integral sliding mode control (ISMC) [3]. Compared to DO method, ISMC method can deal with the system uncertainty which only requires to be bounded. In [4], the authors investigated ISMC controller design issue for fuzzy semi-Markov systems. In [5], a robust fault-tolerant controller was designed for robot manipulators by using ISMC. In addition, for the purposed of improving control performance, optimal control theory can be widely used [6, 7]. In [6], a novel tracking strategy using adaptive dynamic programming (ADP) algorithm was proposed for linear system with unknown dynamics. In [7], a novel value iteration based algorithm was proposed to solve the $H_\infty$ control of linear system. The core mission of optimal control problem for linear system is to solve the algebraic Riccati equation (ARE), and reinforcement learning (RL) technique can effectively handle this issue [8]. In [9], a novel RL scheme based on incremental learning approach was proposed for continuous-time linear system. In order to obviate the requirement of system dynamics, integral RL (IRL) method was proposed [10]. For linear system with input delay, an IRL-based model free optimal control method was proposed, and only the input and output of system datas were used [11].

Inspired by the above content, in this paper, a composite $H_\infty$tracking control scheme is designed for continuous-time linear system with system uncertainty and bounded disturbance by using ISMC and off-policy IRL-based control methods. The sliding mode controller is designed to eliminate the effect of unknown uncertainty. The developed IRL control method is used to obtain the optimal tracking performance under the adverse effect of external disturbance. Furthermore, we introduce a NSV attitude model to show the effectiveness of the proposed control scheme.

2 Problem Description

In this paper, we consider the following uncertain system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( t\right) =Ax\left( t\right) +Bu\left( t\right) +E\varpi (x)+D\varsigma (t) \\ y\left( t\right) =Cx\left( t\right) \end{array} \right. \end{aligned}$$

(1)

where $x(t) =[x_1(t), \cdots , x_n(t)] ^{T}\in \Re ^n$ denotes the system state, $y\left( t\right) \in \Re ^{p}$, $\varpi (x)\in \Re ^{v}$ and $\varsigma (t)\in \Re ^{q}$ represent system output, unknown system uncertainty and external disturbance, respectively. $A\in \Re ^{n\times n}$, $B\in \Re ^{n\times m}$, $C\in \Re ^{p\times n}$, $E\in \Re ^{n\times v}$ and $D\in \Re ^{n\times q}$ are known system matrices. The external disturbance is assumed to belong to $L_{2}\left[ 0,\infty \right)$ . The system uncertain $\varpi (x)$ is bounded and satisfies $\left\| \varpi (x)\right\| \le \varpi _{m}$.

The desired reference trajectory is generated by

$$\begin{aligned} \left\{ \begin{array}{c} \dot{x}_{r}\left( t\right) =A_{r}x_{r}\left( t\right) \\ y_{r}\left( t\right) =C_{r}x_{r}\left( t\right) \end{array} \right. \end{aligned}$$

(2)

where $x_{r}\left( t\right) \in \Re ^{n_{r}}$ and $y_{r}\left( t\right) \in \Re ^{p}\$are system state and output of reference trajectory system.$\ A_{r}$ and $C_{r}$ are constant matrices. Furthermore, the following tracking error can be defined as $e(t) =y(t) -y_{r}(t)$

Here, we introduce a new error variable as

$$\begin{aligned} z\left( t\right) =x\left( t\right) -Gx_{r}\left( t\right) \end{aligned}$$

(3)

where $z \left( t\right) \in \Re ^{n}$, $G\in \Re ^{n\times n_{r}}$ is the constant matrix satisfying $AG+BH=GA_{r}$ and $CG=C_{r}$. $H\in \Re ^{m\times n_{r}}$ is the constant matrix, which is employed to model match. Furthermore, one can deduce that $e(t) =Cz (t)$.

Then, combining (1), (2) and (3), we can obtain

$$\begin{aligned} \dot{z}\left( t\right) =Ax\left( t\right) +Bu\left( t\right) +E\varpi (x)+D\varsigma (t)-GA_{r}x_{r}\left( t\right) \end{aligned}$$

(4)

The control input is designed as $u\left( t\right) =u_{a}\left( t\right) +u_{o}\left( t\right)$, where $u_{a}\left( t\right)$ is an integral sliding mode control policy to eliminate the influence of the system uncertainty, and $u_{o}\left( t\right)$ is an off-policy IRL-based $H_{\infty }$ control policy to guarantee the optimal tracking performance.

3 Controller Design

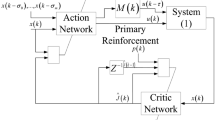
In this section, we will present the porposed control method including ISMC and of-policy IRL-based $H_{\infty }$ control design. Moreover, the structure of the proposed control method is shown in Fig. 1.

Fig. 1.

Estimation results of the unknown disturbance D

3.1 Integral Sliding Mode Control Design

In this paper, we select the following integral sliding mode surface

$$\begin{aligned} \mathcal {S}\left( z ,t\right) =\varGamma [z (t)-z(0)-\int _{0}^{t}\left( Az +Bu_{o}+D\varsigma \right) \mathrm {d\tau }] \end{aligned}$$

(5)

where $\varGamma$ is a positive matrix to be designed, which satisfies $\varGamma B$ is invertible. Furthermore, the integral sliding mode control policy can be designed as

$$\begin{aligned} u_{a}(t)=-\varUpsilon \left( \varGamma B\right) ^{-1}\mathrm {Sgn}\left( \mathcal {S} \right) -B^{-1}\left( AGx_{r}(t)-GA_{r}x_{r}(t)\right) \end{aligned}$$

(6)

where $\mathrm {Sgn}\left( \mathcal {S}\right) =\left[ \begin{array}{ccc} \mathrm {sgn}\left( \mathcal {S}_{1}\right)&\ldots&\mathrm {sgn}\left( \mathcal {S}_{n}\right) \end{array} \right] ^{T}$, and sgn$\left( \cdot \right)$ is a sign function. $\varUpsilon$ is positive matrix to be designed.

Theorem 1

Considering system (4), the integral sliding mode surface and the integral sliding mode control policy are designed as (5)–(6), respectively. Then, integral sliding surface is uniformly asymptotically stable by selecting suitable $\varUpsilon$ and $\varGamma$.

Proof

The Lyapunov function is selected as follows

$$\begin{aligned} V(t) =\frac{1}{2}\mathcal {S}^{T}\mathcal {S} \end{aligned}$$

(7)

Taking derivative of $V\left( t\right)$ with respect to t, one can obtain that

$$\begin{aligned} \dot{V}\left( t\right)= & {} \mathcal {S}^{T}\varGamma [Ax(t)+Bu_{a}(t)+E\varpi (x)-GA_{r}x_{r}(t)-Az (t)] \nonumber \\= & {} \mathcal {S}^{T}\varGamma [-\varUpsilon \varGamma ^{-1}\mathrm {Sgn}(\mathcal { S})+E\varpi (x)] \nonumber \\= & {} -\varUpsilon \mathcal {S}^{T}\mathrm {Sgn}(\mathcal {S})+\mathcal {S}^{T}\varGamma E\varpi (x) \nonumber \\\le & {} -\lambda _{\min }\left( \varUpsilon \right) \left\| \mathcal {S} \right\| +\varGamma E\varpi _{m}\left\| \mathcal {S}\right\| \nonumber \\\le & {} -(\lambda _{\min }\left( \varUpsilon \right) -\varGamma E\varpi _{m})\left\| \mathcal {S}\right\| \end{aligned}$$

(8)

By selecting suitable matrixes $\varUpsilon$ and $\varGamma$ such that $\lambda _{\min }\left( \varUpsilon \right) >\varGamma E\varpi _{m}$, then, we have $\dot{V} \left( t\right) <0$, which means that sliding mode surface is uniformly asymptotically stable.

3.2 Off-Policy IRL-Based $H_{\infty }$ Control Design

Consider the following auxiliary error system

$$\begin{aligned} \dot{z}\left( t\right) =Az\left( t\right) +Bu_{o}\left( t\right) +D\varsigma \left( t\right) \end{aligned}$$

(9)

The corresponding infinite horizon performance index is

$$\begin{aligned} \mathcal {J}\left( z,u_{o},\varsigma \right) =\int _{0}^{\infty }(z ^{T}Qz +u_{o}^{T}Ru_{o}-\varphi ^{2}\varsigma ^{T}\varsigma )\mathrm {d}\tau \end{aligned}$$

(10)

where $Q=Q^{T}\ge 0$, $R=R^{T}>0$ denote the state and control performance weights, respectively. $\varphi$ is a constant, which satisfies $\varphi \ge \varphi ^{*}$, $\varphi ^{*}$ is the smallest $L_{2}$ gain. We consider $\varsigma \left( t\right)$ as opponent’s policy. The aim is to find a control policy $\left( u_{0},\varsigma \right)$ to make system (9) is stable and meets a $H_{\infty }$ performance.

Furthermore, the $H_{\infty }$ control issue is equivalent to following zero-sum game problem

$$\begin{aligned} \mathcal {V}^{*}\left( z\right)= & {} \min _{u_o}\max _{\varsigma }\mathcal {J} \left( z,u_{o},\varsigma \right) \nonumber \\= & {} \min _{u}\max _{\varsigma }\int _{0}^{\infty }(z ^{T}Qz +u_{o}^{T}Ru_{o}-\varphi ^{2}\varsigma ^{T}\varsigma )\mathrm {d}\tau \end{aligned}$$

(11)

where $\mathcal {V}^{*}\left( z _{0}\right)$ is the optimal value function. Control policy and disturbance policy are considered as two hostile players, where control policy desires to minimize the performance index while disturbance policy aims to damage it. Furthermore, we denote control policy $u_{o}(t)=-Kz (t)$ and disturbance policy $\varsigma (t)=K_{w}z (t)$, respectively. Then, the value function can be expressed as

$$\begin{aligned} \mathcal {V}\left( z \right) =z ^{T}(t)Pz (t) \end{aligned}$$

(12)

Moreover, we can obtain the following algebraic Riccati equation

$$\begin{aligned} A^{T}P^{*}+P^{*}A+Q-P^{*}BR^{-1}B^{T}P^{*}+\varphi ^{-2}P^{*}D^{T}DP^{*}=0 \end{aligned}$$

(13)

the saddle point of zero-sum game is

$$\begin{aligned} u_{o}^{*}(t)= & {} -Kz (t)=-R^{-1}B^{T}P^{*}z (t) \nonumber \\ \varsigma ^{*}(t)= & {} K_{w}z (t)=\varphi ^{-2}D^{T}P^{*}z (t) \end{aligned}$$

(14)

Then, system (9) can be rewritten as

$$\begin{aligned} \dot{z}\left( t\right) =\tilde{A}z(t)+B\left( u_{0}\left( t\right) +Kz(t)\right) +D\left( \varsigma \left( t\right) -K_{w}z(t)\right) \end{aligned}$$

(15)

where $\tilde{A}=A-BK+DK_{w}$.

Furthermore, we can obtain that

$$\begin{aligned} z^{T}(t+T)P_{i}z(t+T)-z^{T}(t)P_{i}z(t)= & {} -\int _{t}^{t+T}z^{T}Q_{i}z\mathrm { d}\tau \nonumber \\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! +\, 2 \int _{t}^{t+T}[(u_{o}+K_{i}z(t))^{T}R_{i}K_{i}z(t)]\mathrm {d}\tau \nonumber \\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!-2\varphi ^{2}\int _{t}^{t+T}[(K_{wi}z(t)-\varsigma )^{T}K_{i}z(t)]\mathrm {d}\tau \end{aligned}$$

(16)

Then, the left-hand of (9) can be rewritten as

$$\begin{aligned} z^{T}(t+T)P_{i}z(t+T)-z^{T}(t)P_{i}z(t)=\tilde{P}_{i}^{T}[z^{T}(t+T)\otimes z^{T}(t+T)-z^{T}(t)\otimes z(t)] \end{aligned}$$

(17)

where

$$\begin{aligned} \tilde{P}_{i}= & {} \left[ P_{i11},2P_{i12},\cdots ,2P_{i1n},P_{i22},2P_{i23},\cdots ,P_{inn}\right] ^{T} \\ z^{T}\otimes z^{T}= & {} \left[ z_{1}^{2},z_{1}z_{2},\cdots ,z_{1}z_{n},z_{2}^{2},z_{2}z_{3},\cdots ,z_{n}\right] ^{T} \end{aligned}$$

Similarly, we can deduce

$$\begin{aligned} z^{T}Qz= & {} (z^{T}\otimes z^{T})vec(Q) \nonumber \\ (u_{o}+K_{i}z)^{T}RK_{i}z= & {} [(z^{T}\otimes z^{T})(I_{n}\otimes K_{i}^{T}R) \nonumber \\&+(z^{T}\otimes u^{T})(I_{n}\otimes R)]vec(K_{i}) \nonumber \\ \varphi ^{2}(K_{wi}z(t)-\varsigma )^{T}K_{i}z(t)= & {} [(z^{T}\otimes z^{T})(I_{n}\otimes \varphi ^{2}K_{wi}^{T}) \nonumber \\&-(z^{T}\otimes \varsigma ^{T})\left( \varphi ^{2}I\right) ]vec(K_{wi}) \end{aligned}$$

(18)

From (17) and (18), (16) can be represented as

$$ \varPi _{i}\times \left[ \begin{array}{c} \tilde{P}_{i} \\ vec\left( K_{i+1}\right) \\ vec\left( K_{wi+1}\right) \end{array} \right] =\varOmega _{i} $$

where $\varOmega _{i}=-\gamma _{zz}vec\left( Q\right)$ and

$$\begin{aligned} \varPi _{i}= & {} \left[ \begin{array}{c} \pounds _{zz} \\ -2[\gamma _{zz}(I_{n}\otimes K_{i}^{T}R)+\pi _{zu_{0}}(I_{n}\otimes R)] \\ 2[\gamma _{zz}(I_{n}\otimes K_{wi}^{T}\varphi ^{2})+\phi _{zz}(\varphi ^{2}I_{n})] \end{array} \right] ^{T} \\ \pounds _{zz}= & {} \left[ \begin{array}{cccc} \tilde{z}\left( t_{1}\right) -\tilde{z}\left( t_{0}\right)&\tilde{z}\left( t_{2}\right) -\tilde{z}\left( t_{1}\right)&\cdots&\tilde{z}\left( t_{l}\right) -\tilde{z}\left( t_{l-1}\right) \end{array} \right] ^{T} \\ \gamma _{zz}= & {} \left[ \begin{array}{cccc} \int _{t_{0}}^{t_{1}}z\otimes z\mathrm {d}\tau&\int _{t_{1}}^{t_{2}}z\otimes z \mathrm {d}\tau&\cdots&\int _{t_{l-1}}^{t_{l}}z\otimes z\mathrm {d}\tau \end{array} \right] ^{T} \\ \pi _{zu_{o}}= & {} \left[ \begin{array}{cccc} \int _{t_{0}}^{t_{1}}z\otimes u_{o}\mathrm {d}\tau&\int _{t_{1}}^{t_{2}}z \otimes u_{o}\mathrm {d}\tau&\cdots&\int _{t_{l-1}}^{t_{l}}z\otimes u_{o} \mathrm {d}\tau \end{array} \right] ^{T} \\ \phi _{z\varsigma }= & {} \left[ \begin{array}{cccc} \int _{t_{0}}^{t_{1}}z\otimes \varsigma \mathrm {d}\tau&\int _{t_{1}}^{t_{2}}z\otimes \varsigma \mathrm {d}\tau&\cdots&\int _{t_{l-1}}^{t_{l}}z\otimes \varsigma \mathrm {d}\tau \end{array} \right] ^{T} \end{aligned}$$

Furthermore, we have

$$ \left[ \begin{array}{c} \tilde{P}_{i} \\ vec\left( K_{i+1}\right) \\ vec\left( K_{wi+1}\right) \end{array} \right] =\left( \varPi _{i}^{T}\varPi _{i}\right) ^{-1}\varPi _{i}^{T}\varOmega _{i} $$

Then, the online implementation of off-policy IRL-based $H_{\infty }$ control method is presented in Algorithm 1. Moreover, the stability analysis of the system (9) can be reference to [10].

4 Simulation Results

In this section, simulation studies are employed to verified the effectiveness of the proposed method. The nonlinear attitude mode of NSV is linearized at equilibrium point $x_{0}=[-0.0005,0.0001,0.2,0,-0.1872,0.0007]^{T}$, such the linear attitude mode of NSV is obtained.

$$ \dot{x}=Ax+Bu $$

where $x=[\alpha ,\beta ,\mu ,p,q,r]^{T}$ is system state vector, which are attitude angles and angle rates. $u=[\delta _{e},\delta _{a},\delta _{r},\delta _{x},\delta _{y},\delta _{z}]^{T}$ denotes control input vector. The specific information of NSV mode and matrices A, B can reference to [12]. And

$$\begin{aligned} D= & {} E=\left[ \begin{array}{cccccc} 0.1&0.4&0.1&0.2&0.1&0.2 \end{array} \right] ^{T} \\ \varpi (x)= & {} 0.01\sin (x_{1})+0.05x_{2}^{2}\cos (x_{3})\varsigma (t)=0.01e^{-0.1t}\sin (0.1t) \end{aligned}$$

Fig. 2.

Convergence of matrix P and sliding surface function.

Fig. 3.

The state responses of the open-closed system.

Fig. 4.

The responses of the attitude angles.

The reference attitude angles are selected as

$$ \dot{x}_{r}=0,\alpha _{r}=0,\beta _{r}=-0.8,\gamma _{r}=0.65 $$

For algorithm 1, the parameters are chosen as follows: $Q=10^{4}I,$ $R=I.$ From $t=0$ s to $t=2$ s, the following exploration noise is employed as system input

$$ \bar{e}=100\sum _{c=1}^{100}\sin \left( w_{c}t\right) $$

where $c=1,...,100$, and $w_{c}$ are selected from $[-500,500]$. Moreover, the weighting matrices are $\varPi =I,Q=10^{4}I,$ $R=I$, and $\varphi =1.5$, $\varGamma =2.2$, $\varUpsilon =0.01$. Furthermore, by using Algorithm 1, the control gain K can be obtained. The convergence process of P matrix element and sliding surface function are shown in Fig. 2. From Fig. 3, it can be observed that system is unstable without the control input. Then, it can be seen from Fig. 4 that actual angles can well track the desired signals in a short time, which means that the proposed control method is effective.

$$ K\!\!=10^{2}\times \!\!\left[ \begin{array}{cccccc} \!\!3.7617 &{} \!\!-0.4746&{} \!\!-0.6895&{} \!\!-0.7123\!\! &{} 0.9036\!\! &{}-0.5118\!\! \\ 5.1117 &{} \!\!1.2282 &{} \!\!1.2564&{} \!\!1.2707 &{} \!\!2.5080&{} \!\!1.007 \\ \!\!-2.5063 &{} \!\!-2.0072&{} \!\!-2.7337 &{} \!\!-2.7688 &{} \!\!-2.6176 &{} \!\!-2.8739\\ \!\!-0.4758&{} \!\!-0.5955&{} \!\!-0.6830&{} \!\!-0.6959 &{} \!\!-0.5633 &{} \!\!-0.5337 \\ \!\!-0.0510&{} \!\!-0.0437&{} \!\!-0.0583 &{} \!\!-0.0592 &{} \!\!-0.054305 &{} \!\!-0.0584\\ \!\!1.1612&{} \!\!0.0907 &{} \!\!0.0640 &{} \!\!0.0627 &{} \!\!0.4401 &{} \!\!0.0545\!\! \end{array} \right] $$

5 Conclusions

In this paper, a composite $H_\infty$tracking control scheme is designed for continuous-time linear systems with system uncertainty and bounded disturbance. Firstly, the integral sliding mode controller has been applied to deal with unknown system uncertainty. In addition, an off-policy IRL has been provided for solving the two-player zero-sum game problem of $H_\infty$ control. Finally, the simulation results for NSV attitude control show the effectiveness of the proposed method. In our future work, we will extend the results to nonzero-sum games for practical system.