Two-Stage Flocking Formation Control Based on Constrained Boundary

Abstract

Flocking is a special behavior that exists in the natural world. In this paper, a two-stage flocking formation algorithm is presented. The algorithm utilizes a varied range boundary to limit the agents in the group. As time increases, the agents tend to form an $\alpha -lattice$ structure formation. The algorithm improved the converging speed of the flock formation. Simulations and analysis are provided to demonstrate the algorithm for 2D cases.

1 Introduction

In animal herds, a unique large group behavior existed is called “Flocking” [9], which refers to a large number of individuals interacting with each other. This behavior is prevalent to see in the natural world, such as the migration of wildebeest in East Africa, a school of fish salmon avoiding the predation of sea lions, and the doves hovering above a square freely but organized without a leader.

The flocking phenomenon is very enlightening for engineering practice [6, 11]. In modern society, the behavior of large groups of automated vehicles becomes more and more essential and gradually comes to the front. By 2030, more than 20 million Tesla pure electrical cars will be sold annually, which means there will be one in ten cars that are self-driving on the roads. Although each automated car may be smart enough to avoid collision and find the optimal route to the destination, from a higher-level perspective, the large group of smart cars are exactly a flock, and the dynamics of it possess the properties of flocking.

On the other hand, flocking behavior is still a very challenging topic for researchers [2, 4, 8, 14]. The first thing for studying the flocking behavior is to understand how the flock is formed. Reynolds [12] initialized three necessary rules for forming a flock: First, the individual must not collide with other agents in the group. Second, each individual has to match the velocity with others while moving along with the group. Third, every individual in the group should stay close to its neighbors. These three basic rules formulate the basics for flocking. The first rule regulates the minimum distance between individuals in the flock so that they will not crash while moving; the second rule guarantees the group of agents can move in a particular flock formation. Furthermore, the last rule ensures the flock will not be torn apart by the accumulation effects of the former two rules as time passes by.

The main contents of this paper are divided into four parts. The first section states the preliminaries, including basic concepts of graph theory, the dynamic agents, and the $alpha-lattice$ structure; the second section discusses the problem of flocking and presents an algorithm to solve the problem. Experiments show the effects of the algorithm in the third section, and then the paper is concluded in the last part.

2 Preliminaries

In this section, the application of graph theory in flock forming and moving control are discussed. The basic concepts of graph theory and how they are applied to flocking are introduced. Also, the $\alpha -lattices$ structure is presented as it has been utilized to form the basic bricks of the flock.

2.1 Graph Topology of Flocks

A graph G consists of vertices set $\mathcal {V}={1,2...n}$ and edges set $\mathcal {E} \in \{(i,j):i,j \in \mathcal {V},i \ne j\}$ [3, 5]. Each agent in the flock is represented as a node, $i\in \mathcal {V}$, and the relationship between two communicating nodes (i, j) is represented as an edge e(i, j). If the $e(i,j)\in \mathcal {E} \longleftrightarrow e(j,i) \in \mathcal {E}$ for all edges, then the graph is said to be undirected. The interconnection relationship among nodes in the graph is represented by an adjacency matrix $\mathbf {A}=a[i,j]:i \in V, j \in V$. For $a[i,j] \ne 0$, then $e(i,j) \in \mathcal {E}$. If the graph is undirected and unweighted, the adjacency matrix is symmetric ($\mathbf {A = A^T}$)and the elements in $\mathbf {A}$ satisfy:

$$\begin{aligned} a_{ij} = \left\{ \begin{array}{lr} 1, \quad i=j &{} \\ 0, \quad otherwise &{}\\ \end{array} \right. \end{aligned}$$

(1)

The neighbors of a node i in an undirected graph are defined as $N_i = \{j \in \mathcal {V}:a_{ij} =1 ,i \ne j, (i,j) \in \mathcal {V}\}$.

2.2 Dynamics of Agents

Consider a group of dynamic agents. The individual agent can communicate with others, and they can exchange the position and velocity information of themselves. Let the communication range for agents is $R \in \mathbb {R}$, and the safe distance between agents is $D \in \mathbb {R}$. The motion of agents [13] is described as:

$$\begin{aligned} \left\{ \begin{array}{lr} \dot{q_i} = p_i, &{}\\ \dot{p_i} = u_i \end{array} \right. \end{aligned}$$

(2)

where $q_i \in \mathbb {R}^{n}(n = 2,3)$ represents position information of agent i, and $p_i \in \mathbb {R}^{n}(n = 2,3)$ represents the velocity of agent i. $u_i \in \mathbb {R}^{n}(n = 2,3)$ is the control input, which represents the acceleration for agent i in its moving direction.

For an agent i in the flock, its neighbors can be defined as:

$$\begin{aligned} N_i = \{j \in \mathcal {V},j \ne i:||q_j-q_i|| < R\} \end{aligned}$$

(3)

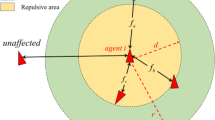
where $\Vert *\Vert$ is the Euclidean norm in cartesian coordinate system, and R is the maximum communication range between agent i and agent j. From the Eq. 3, one can know for an agent i, the communication scope is a circle with radius R. Let $d_{ij}$ expresses the distance between two agents, then:

$$\begin{aligned} d_{ij} = \Vert q_j-q_i\Vert , \quad \forall {j} \in N_i \end{aligned}$$

(4)

To fulfill the first rule of Reynolds, i.e. every agent should not collide with each other, then, $D<= d_{ij} <= R$. To further regulates the safe distance and the communication range, we have:

$$\begin{aligned} R = \kappa D, \quad \kappa >=1 \end{aligned}$$

(5)

For a graph G, the proximity net $G(q) = (\mathcal {V},\mathcal {E}(q))$ [1] satisfies:

$$\begin{aligned} \mathcal {E}(q) = \{e(i,j): (i,j)\in \mathcal {V} \times \mathcal {V}, d_{ij} < R, i \ne j\} \end{aligned}$$

(6)

2.3 Basic Brick: $\alpha$-lattices

There are many types of flock structure exits, and the $absolute-\alpha -lattice$ structure is one of the most basic structures. To form a $\alpha -lattice$ structure flock, the distance between every pair of nodes must be equal to a fixed number d:

$$\begin{aligned} d=d_{ij} = \Vert q_j-q_i\Vert \quad \forall j \in N_i \end{aligned}$$

(7)

In general, the $\alpha -lattice$ structure is common to see in the natural world, but the absolute $\alpha -lattice$ is hard to form. Therefore, the constraint for forming flock by using 7 could be relaxed to :

$$\begin{aligned} d_{quasi} =d_{ij} = \Vert q_j-q_i\Vert \in [d - \delta , d + \delta ] \quad \forall j \in N_i \end{aligned}$$

(8)

where $\delta$ is a small distance for forming the relaxed $quasi-\alpha -lattice$(or quasi-crystals) [13]. Also we could define the deviation function to measure how much the $quasi-\alpha -lattice$ structure is different from the $absolute-\alpha -lattice$ structure [10]:

$$\begin{aligned} f= \frac{1}{\Vert \mathcal {E}(q) + 1\Vert } \sum _{i=1}^{n}\sum _{j\in N_i} \varPsi (\Vert \delta _{ij}\Vert ) \end{aligned}$$

(9)

and the pairwise potential function:

$$\begin{aligned} \varPsi (x) = \frac{1}{k}(\frac{1}{\frac{1}{z}+1}e^{(\frac{1}{z} x + 1)} -e) \end{aligned}$$

(10)

where $\delta _{ij} = d_{quasi} - d$, and $z > 0$.

The pairwise energy function has purposes for measuring the deviation energy of the formation in which it differs from $\alpha -lattice$. When z is small, it is similar to the quadratic equation on the x coordinate. The deviation energy will increase quickly as the $\delta$ value increases. However, as z increases, the pairwise potential function in the former stage($x>0$) increases slower, which means that if the $\delta$ value is within a certain range, the deviation could be tolerated or alleviated, but when the $\delta$ value is getting bigger, then the punishment increases faster. A non-negative map called $\sigma$ norm [10] is defined so that the distance could be differentiable at zero:

$$\begin{aligned} \Vert x\Vert _\sigma = \sqrt{1+\frac{1}{a}\Vert x\Vert ^2}-1 \quad a\in [0,\infty ] \end{aligned}$$

(11)

Also a bump function 12 is utilized to construct a smooth potential function [10]:

$$\begin{aligned} \varLambda _{h}(z)= \left\{ \begin{array}{lr} 1, &{} z\in [0,h]\\ \frac{1}{2}[1+sin(\pi \frac{(z-h)}{(1-h)}+\frac{\pi }{2})], &{} z \in [h,1]\\ 0, &{} \textit{otherwise} \end{array} \right. \end{aligned}$$

(12)

where $h \in (0,1)$. Then, an adjacent matrix on the proximity function G(q) could be:

$$\begin{aligned} \mathbf {A(q)}=a_{i j}(q)= \left\{ \begin{array}{lr} \varLambda _{h}\left( \left\| d_{ij}\right\| _{\sigma } / \Vert r\Vert _{\sigma }\right) \in [0,1], &{} j \ne i\\ 0, &{} i = j \end{array} \right. \end{aligned}$$

(13)

The adjacency matrix is an indicator function that $a_{ij} = 0$ when $h=1$. This can be interpreted as the parameter h is controlling the adjacent range by the ratio of actual distance between two agents and the communication range in $\sigma$ domain.

2.4 Control Forces

Flocking of agents depends on three forces: the force to avoid neighboring agents, the force to make individual agents reach a consensus state, and the force to track objectives. Therefore, three control input is generated to form and moving the flocks. Olfati-Saber [13] proposed the control protocols with obstacle avoidance based on three types of agents: $\alpha$ agent, $\beta$ agent, and $\gamma$ agent. The control protocols in Olfati-Saber’s third algorithm for individual agent i is:

$$\begin{aligned} u_i = u^{\alpha }_i + u^{\beta }_i + u^{\gamma }_i \end{aligned}$$

(14)

where each of the three controls are:

$$\begin{aligned} u^{\alpha }_i = \zeta ^\alpha _1\sum _{j \in N^{\alpha }_i} \phi _\alpha ( \Vert d_{ij}\Vert _{\sigma } ) \mathbf {W}_{ij} + \zeta ^\alpha _2 \sum _{j\in N^{\alpha }_i} a_{ij}(q)(p_j-p_i) \end{aligned}$$

(15)

$$\begin{aligned} \phi _{\alpha }(z)=\varLambda _{h}\left( z / r_{\alpha }\right) \left( z / \sqrt{1+(z-\Vert d\Vert _\sigma )^{2}}\right) \end{aligned}$$

(16)

where the $\mathcal {W}_{i,j}$ is the gradient of the $\sigma$ map function:

$$\begin{aligned} \mathbf {W}_{ij} = \nabla \sigma (q) = \frac{q_j-q_i}{a \sqrt{1+ \frac{1}{a} {\Vert d_{ij}\Vert }^2}} = \frac{{q_j-q_i}}{1+a\Vert d_{ij}\Vert _\sigma } \end{aligned}$$

(17)

Similarly, the $u^{\beta }_i$ is:

$$\begin{aligned} u^{\beta }_i = \zeta ^{\beta }_1\sum _{j \in N^{\beta }_i} \phi _\beta ( \Vert \widetilde{d_{ij}}\Vert _{\sigma } ) \mathbf {\widehat{W}}_{ij} + \zeta ^{\beta }_2\sum _{m\in N^{\beta }_i} b_{im}(q)(\hat{p_{m}}-p_i) \end{aligned}$$

(18)

$$\begin{aligned} \phi _{\beta }(z)=\varLambda _{h}\left( z / d_{\beta }\right) \left( \sigma _{1}\left( z-d_{\beta }\right) -1\right) \end{aligned}$$

(19)

$$\begin{aligned} b_{im}(q)=\varLambda _{h}\left( \left\| \hat{q}_{im}-q_{i}\right\| _{\sigma } / d_{\beta }\right) \end{aligned}$$

(20)

where the $\Vert \widetilde{d_{ij}}\Vert _{\sigma }$ represents sigma distance between the $\beta$ agent j and agent i, and the $\mathbf {\widehat{W_{im}}}$ is:

$$\begin{aligned} \mathbf {\widehat{W}}_{im} = \nabla \sigma (q) = \frac{q_{m}-q_i}{a \sqrt{1+ \frac{1}{a} {\Vert d_{im}\Vert }^2}} = \frac{{q_{m} - q_i}}{1+a\Vert d_{im}\Vert _\sigma } \end{aligned}$$

(21)

where the letter m represents a virtual $\beta$ agent sticking around the surface of the obstacles, and for the $\gamma$ agent:

$$\begin{aligned} u_{i}^{\gamma }=-\zeta _{1}^{\gamma } \sigma _{1}\left( q_{i}-q_{m}\right) -\zeta _{2}^{\gamma }\left( p_{i}-p_{m}\right) \end{aligned}$$

(22)

The $\beta$ agents produce external repulsive force to prevent the flock from crashing into the obstacles. The $\alpha$ agents and the $\gamma$ agents form the $\alpha -lattice$ structured flock and trace a dynamic or static target. Without the $\alpha$ agents, the flock will eventually become fragmented because of the repulsive force among nodes. The repulsive force can change agents’ initial speed and speed direction, and the agents will go fragmented when nothing restricts them.

Finally the velocity and position update protocol are:

$$\begin{aligned} V^{i}_{new} = V^{i} + u_i \varDelta t ,\quad P^{i}_{new} = P^{i} + V^{i} \varDelta t + u_i\frac{(\varDelta t)^2}{2} \end{aligned}$$

(23)

where $V^{i}\in \mathbb {R}^n, (n=2,3)$ is the velocity of agent, and $P^{i} \in \mathbb {R}^n, (n=2,3)$ is the position of agent i.

Fig. 1.

Initial distribution: red disk is the obstacles, green point is the target

3 Constrained Flocking Formation

Reza Olfati-Saber [13] proposed several algorithms for forming $\alpha$ lattice flock utilizing a multi-species framework. Th flock formed eventually becomes a lattice-like shape and can chase static or moving objects. However, the algorithms proposed by Reza [13] cannot realize formation control and strongly depend on the parameter settings. Inappropriate parameter settings will bring fragmentation to the flock. Also, if the initial distributions of individuals are too separated and the communication range for agents is limited, the flock will not be formed. Even if the majority of the agents are formed a flock, it is still possible to lose some outliers who have no neighbors at all in the beginning for an extended period. In this section, a constrained flocking formation is proposed to solve this problem by using a constrained boundary at the beginning of the formation.

3.1 Long Time Convergence

Fig. 2.

The group of agents hasn’t form complete flock until they meet the obstacles

Using Olfati’s algorithm with the initial position of agents set as $\mathcal {X,Y} \sim U(0,200)$ (Fig. 1) and sensing distance set as 10, the result shows that the group of agents will spend a long time converging to a flock if the target is set far from the group’s initial position (Fig. 2).

3.2 Constrained Flocking Shape Formation

In this section, a boundary constrained algorithm is presented for controlling the initial flocking formation shape. Using a virtual constraint boundary, the flock is formed much quicker than merely using a single target point. The flocking process is divided into two stages. In the first stage, the agents are constrained to form an $\alpha -lattice$ structured shape that can support them to fly together later. After the formation is complete, the constrained boundary is eliminated, and the flock starts chasing their predetermined target.

3.3 Algorithms

To achieve the first stage of convergence, the group of agents has to find the central position of the flock as the initial target. Whenever the distance between agents is close enough, which means agents can sense others, they will establish connections. Also, a time-varied-ranged constraints boundary is built to prevent agents from flying out of scope and give an initial push to the agents initialed on the boundary. To achieve a line boundary, the following lemma is used:

Lemma 1

For a hyperplane boundary with unit normal $\mathcal {O}_{m}$ and passes through the point m,the position and velocity of the $\beta$ agent are determined by:

$$\begin{aligned} \hat{q}_{i, m}=K q_{i}+(I-K)m ,\quad \hat{p}_{i, m}=K p_{i} \end{aligned}$$

(24)

where $\hat{q}_{i, m}$ is the point that the boundary passes through, and $K = I-\mathcal {O}_{m}\mathcal {O}^{T}_{m}$, and the safe range between obstacles and agents could be changed by time $D(t)_m \propto \epsilon t,\epsilon \in \mathbb {R}$.

Proof

See [10] Lemma 3

With Lemma 1, the next thing is to determine how many point we need so that they can form a line. Consider a line with width $D^{'}$, assume the initial desired distance from the wall is $D_m(0)$, the number of points needed n is easy to calculate, and the control input is also modified: $n = \textit{roundoff}(\frac{D^{'}}{D(0)_m})+1$ and the $\gamma$ control input is changed to $u_i = u^{\alpha }_i + u^{\beta }_i + u^{\gamma ^{'}}_i$, where $u^{\gamma ^{'}}_i$is modified to:

$$\begin{aligned} u^{\gamma ^{'}}_i = -\zeta _{1}^{\gamma ^{'}} \sigma _{1}\left( q_{i}-q_{m}\right) + \textit{Constant} \end{aligned}$$

(25)

We can use the relative connectivity [7, 13] to judge when to stop the first stage and go to the second stage:

$$\begin{aligned} C=(1 / n-1) {\text {rank}}(\mathbf {A}^{'}(G(q))) \in [0,1] \end{aligned}$$

(26)

where $\mathbf {A}^{'}$ is the [0–1] indicator adjacent matrix (not the spatial adjacent matrix defined by 13).

4 Experiment

Due to the limited length of this article, the experiment only shows Stage 1 as the algorithm shows. The experiment selects 100 nodes with a size of 10 randomly distributed in a square region centered at 0, and the distribution of X,Y coordinates complys $\mathcal {X,Y} \sim U(0,300)$ in a 2D plane. The boundary set is bigger than the distributed region of agents. The parameter for the control is set as $c^{\alpha }_1 = 40$, $c^{\beta }_1 =1500$, $c^{\gamma }_1 = 60$.

Fig. 3.

Constrained flock formation

Figure 3 shows the evolution of the formation of the flock. The agents are assigned a random direction and velocity in the beginning. The green boundary limits the agents so that they will not fly out by random movement. The green point is the stage 1 target, which produces a centripetal force for all agents. Also, every agent will have the pairwise resisting force to avoid the collision, and the boundary also produces resisting force to alter the velocity and direction of the agents who are close to it. Figure 4 shows the shape and statistical network properties of the flock at $t = 0$ s and $t=12$ s (0.1 s is the step size). In the beginning, the degree, clustering coefficient, and the number of triangles that pass through each agent are small or zero, but after the $\alpha$-lattice structure is formed, the values are changed and tend to be stable. The trajectories plot Fig. 5 shows that all agents are going towards center of the flock. However, once the agents have reached the center, they begin changing their directions locally, just like marching on the spot.

Fig. 4.

Flocking formation shape and network attributes

Fig. 5.

Trajectories of agents and the velocities

5 Conclusion

In this paper, the flocking behavior is stated. The problem in the early stage of flock formation is solved by utilizing a constrained boundary algorithm. The experiment results show the converging speed for the flocking formation is improved, and the $\alpha -lattice$ structure is presented in the formation. However, there are still some future works to do to better control the formation of more complex structures, and the algorithm’s complexity is about to be improved further.