Numerical Investigation of Erosion of a Steam Turbine Blade Due to the Impact of Condensed Water Droplets

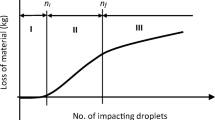
Abstract

Water droplets striking a solid surface at high speeds creates fatigue that results into erosion of the solid surface. This phenomenon is likely to occur in steam turbines and hence it can be very problematic for turbine blade life. At the final stages of the turbine, the steam does not have enough energy to be in the gaseous state so condensation occurs to some extent and liquid droplets form at the trailing edges of the final stator stages. These water droplets travel with steam and continue to hit the rotor stage blades at high impact velocities. This creates high pressures inside the droplets that easily exceeds water hammer pressures for a brief period and then releases which causes fatigue onto the turbine blades in turn eroding the blade. The current research work studies the erosion of steam turbine blade due to the impact of droplets. This study evaluates the one-dimensional model of the droplet striking a solid surface which is obtained by combining the fluid model and the solid model. The fluid model is simply a wave equation of the pressure wave fronts inside the droplet which is derived from the well-known N-S equations. The solid model is also a wave equation for the deformation of the turbine blade when struck by the high-speed droplet. Parametric studies are carried out to investigate the effect of parameters such as impact speed and turbine blade material on pressure and stress of the turbine blade.

1 Introduction

Steam turbine blades are prone to be eroded by the water droplets that are formed by the condensation of steam at the final stages of the stator blades. The water droplets that are deposited are dragged along with the steam flow towards the trailing edge where it gets collected to form larger droplets. These droplets can have the diameter up to 1 mm. When these droplets are torn by the trailing edge, they get scattered and broken into smaller droplets. As the steam expands below saturation line in different stages, it condenses into little droplets of water which lead to nucleation making these water droplets bigger. These water droplets impact the turbine blades at high speeds and cause erosion onto the blade damaging it and lowering its performance over time. Due to this impact, a pressure wave is produced inside the water droplet. This pressure wave inside the water droplet propagates back and forth inside the droplet itself at the speed of sound. If the contact velocity is higher than the velocity of the shock wave inside the water, this wave remains in contact with the solid surface as shown in Fig. 1.

Fig. 1

Schematic of development of shock wave

As the shockwave propagates through the water droplet at the speed of sound, the pressure inside it keeps increasing until the edge of the shockwave detaches the surface of the solid. This is the point where lateral jetting occurs and is the point where the maximum pressure inside the water droplet is seen. This pressure is higher than the water hammer pressure and depends on the velocity of impact. Since the water droplets impact the surface of the material at high impact velocities, compression and non-uniform distribution pressure distribution inside the water droplet occurs. This pressure is what we call water hammer pressure.

$$ p = \rho \times c \times v $$

(1)

As shown in Fig. 2, since the volume of the water is highest at the centre of the surface where the water hits the surface of the material, the maximum pressure is generated at this point of the surface. The water droplet oscillates back and forth inside the droplet itself resisting the change of shape before it performs a radial flow while still in the collision of the surface of the material. This resistance is directly proportional to the impact velocity of the water droplet causing water hammer effect onto the surface of the material. As the shockwave of the pressure wave fronts detach from the contact surface during the radial flow, lateral jetting is produced within the water droplet with the velocities higher than the initial velocity of impact. During the lateral jetting, the pressures inside the water droplet reach its maximum which is much higher than the water hammer pressure of the droplet. This pressure is the most dangerous of all the other pressures as the lateral jetting pressures may reach up to three times more than that of the water hammer pressures.

Fig. 2

Stages of droplet impact on solid surface [1]

As the blade surface gets constantly shot on by the water droplets at high speeds, the stresses induced onto the surface of the blade by these droplets are high which causes water droplet erosion. To reduce these stresses, metal coating is done on the surface of the blade. Coating for water droplet erosion is done with the metal that has a lower Young’s modulus in order to reduce stress.

In the past couple of decades, several efforts have been made to quantify the water droplet erosion. Naib [1] did numerical analysis on water droplet erosion (WDE) for two different metals and compared them. It is seen that the titanium alloy had a better resistance towards WDE when compared to the steel alloy. It is also seen that the impact velocity, impact diameter and impact angle play a major role in determining WDE. Ahmad et al. [2] performed an experimental analysis on the water droplet erosion and observed that the impact velocity is the main factor for determining the peak pressure and stress while Chidambaram et al. [3] carried out three-dimensional numerical analysis of the water droplet erosion and came out with the same conclusion as observed by Ahmad et al. [2]. Li et al. [4] performed one-dimensional numerical analysis of water droplet erosion mechanism and their results showed that the higher the impact velocity results into greater peak pressure and higher stress on the blade. Marzbali [5] in his thesis performed two-dimensional numerical analysis to determine the peak pressures and stresses on the blade and found that the peak pressure occurs not at the instant of impact but after a brief moment and the peak pressure occurs inside the droplet and not at the interface. Huang et al. [6] did a numerical analysis on a 2D axisymmetric model of the water droplet erosion and compared the maximum stresses and pressures for different coating thicknesses. It is seen that the pressures and stresses on the blade are higher for a non-coated blade when compared to a coated blade.

In the present work, a one-dimensional numerical model is developed to study water droplet erosion. This work mainly focuses on comparing the pressure and stress curves of the rigid blade impact model with the elastic blade impact model. Moreover, pressure and stress curves of the blade material 1Cr13 (which has a Young’s modulus of 200 GPa) and a coated blade (which has a Young’s modulus of 100 GPa) are compared to appreciate the effect of coating of steam turbine blade.

2 Problem Description

In the present work, a one-dimensional numerical analysis is carried out on the water droplet erosion over the turbine blade to obtain the pressure curves inside the liquid droplet and stress curves over the surface of the blade. The governing equations consist of two parts one of liquid regime and the other of solid regime. Both are done for linear and nonlinear model. These governing equations are derived from the famous Navier–Stokes equations.

Governing equations. To simplify the Navier–stokes equations to arrive at the governing equations for the present problem, the momentum and viscosity terms are removed. This can be justified by the following reasons. (i) Since, the order of magnitude of the shear viscosity coefficient is low when compared to the density, the viscosity force tensor can be ignored. (ii) Since the shockwave travels at the speed of sound, the momentum cannot travel faster than the shockwave and hence can also be ignored.

Applying these conditions to the Navier–stokes equations, they can be simplified to the following equations.

$$ \frac{\partial \Delta \rho }{{\partial t}} + \nabla .(\rho V) = 0 $$

(2)

$$ \frac{\partial \rho V}{{\partial t}} + \nabla .(\Delta pI) = 0 $$

(3)

For a fluid, Δρ can be written as

$$ \Delta \rho = \frac{\partial \rho }{{\partial p}}\Delta p = \frac{1}{{c^{2} }}\Delta p $$

(4)

Substituting Eq. 4 in Eqs. (2) and (3), the following equations can be obtained.

$$ \nabla^{2} (p) = \frac{1}{{c^{2} }}\frac{{\partial^{2} (p)}}{{\partial t^{2} }} $$

(5)

$$ \nabla^{2} (V) = \frac{1}{{c^{2} }}\frac{{\partial^{2} (V)}}{{\partial t^{2} }} $$

(6)

By introducing the stream function into the equations, Eqs. (5) and (6) can be merged into one equation using the following equations.

$$ V = \nabla \psi $$

(7)

$$ p = - \rho \frac{\partial (\Psi )}{{\partial t}} $$

(8)

The merged Eq. (9) represents a wave equation for the liquid regime.

$$ \nabla^{2} \psi = \frac{1}{{c^{2} }}\frac{{\partial^{2} (\psi )}}{{\partial t^{2} }} $$

(9)

The speed of sound in equation will determine the linearity of the equations. If the value of ‘c’ is taken constant throughout the process, the equation will be turned into a linear partial differential equation.

The equations used for calculating pressure, density and speed of sound are as follows.

$$ p = - \rho \frac{\partial (\Psi )}{{\partial t}} $$

(10)

$$ p = A\rho^{\eta - B} $$

(11)

$$ c = \sqrt {\eta \frac{p + B}{\rho }} $$

(12)

Equation (11) is known as Tait equation of state of water where A, B and η are constants with values being A = 1.0147663 × 10^–19, B = 2.858987 × 10⁸, η = 7.15 [7].

To obtain the linear peak pressures and stresses, Eq. (12) is to be omitted from the set of equations meaning, the speed of sound throughout the water droplet is constant.

If the blade is taken as an elastic blade, the governing equation for solid regime is also added with the liquid regime. Under 1D coordinate system, the elastic solid also obeys the wave equation:

$$ \nabla^{2} U_{{\text{s}}} = \frac{1}{{c_{{\text{s}}}^{2} }}\frac{{\partial^{2} (U_{{\text{s}}} )}}{{\partial t^{2} }} $$

(13)

Boundary conditions. At the interface, the pressure that is induced by the droplet is absorbed by the blade in terms of stress so by equating these two terms, a boundary condition for the solid regime can be obtained as shown in Eq. (14).

$$ \frac{{\partial (U_{{\text{s}}} )}}{\partial x}|_{x = 0} = \frac{{p_{{\text{s}}} |_{x = 0} }}{{E_{{\text{s}}} }} = - \frac{\rho }{{E_{{\text{s}}} }}\frac{\partial \psi }{{\partial t}}|_{x = 0} $$

(14)

For the elastic blade model, the deformation velocity is to be incorporated to the liquid regime boundary condition which is Eq. (7). By doing so, the same transforms into Eq. (15).

$$ \frac{\partial \Psi }{{\partial x}}|_{x = 0} = v_{0} - \frac{{\partial U_{{\text{s}}} }}{\partial t}|_{x = 0} $$

(15)

Initialization of the problem solution is done by substituting the initial values of stream function and deformation to be zero. Table 1 gives a general idea of all the boundary conditions and governing equations that are used to analyse the problem.

Table 1 Boundary conditions

These boundary conditions are used to get the pressure curves inside the water droplet and stress curves on the surface of the blade using FDM discretization.

The discretization is done using 2nd order central difference method with 1st degree accuracy.

$$ \frac{{\partial^{2} \emptyset }}{{\partial x^{2} }} = \frac{{\emptyset_{i + 1}^{n} - 2 \times \emptyset_{i}^{n} + \emptyset_{i - 1}^{n} }}{{\Delta x^{2} }} $$

(16)

$$ \frac{{\partial^{2} \emptyset }}{{\partial t^{2} }} = \frac{{\emptyset_{i}^{n - 1} - 2 \times \emptyset_{i}^{n} + \emptyset_{i}^{n + 1} }}{{\Delta t^{2} }} $$

(17)

The discretized forms of the wave equations are as follows.

$$ \psi_{i}^{n + 1} = c^{2} \times \Delta t^{2} \times \left( {\frac{{\psi_{i - 1}^{n} - 2 \times \psi_{i}^{n} + \psi_{i + 1}^{n} }}{{\Delta x^{2} }}} \right) - \left( {\psi_{i}^{n - 1} - 2 \times \psi_{i}^{n} } \right) $$

(18)

$$ U_{i}^{n + 1} = c_{S}^{2} \times \Delta t^{2} \times \left( {\frac{{U_{i - 1}^{n} - 2 \times U_{i}^{n} + U_{i + 1}^{n} }}{{\Delta x^{2} }}} \right) - \left( {U_{i}^{n - 1} - 2 \times U_{i}^{n} } \right) $$

(19)

Methodology. The following steps are followed to construct a code for the problem at hand.

• 1. The initial values of pressure and displacement are given zero as the water droplet is yet to be disturbed by the impact with the surface.

• 2. The density and sound speed are to be calculated from Eqs. (11) and (12), respectively. (For linear wave model, speed of sound is to be omitted out of the calculations as it is to be kept constant in the stream function wave equation.)

• 3. Stream function (ψ) is to be calculated using the wave Eq. (18) which can be discretized using Eqs. (16) and (17) over the grid using the value of c obtained from the previous step.

• 4. Pressure is to be calculated from Eq. (10) using the density and stream function obtained from the previous steps. (For rigid, stop the 1^st time step here and go to the next time step and redo the steps 1 to 4 until the pressure difference between consecutive time steps reach specific threshold.)

• 5. The pressure at this time step is to be taken as the boundary condition for the solid region as in Eq. (14).

• 6. Using these values of displacement (U), the displacements at the next time step are to be calculated using the displacement wave Eq. (19)

• 7. This displacement is to be used to calculate the velocity at which the deformation occurs at the interface

• 8. This velocity is used as the boundary condition of the liquid region (15).

• 9. Move to the next time step.

• 10. These steps 2–9 are to be repeated until the desired threshold pressure difference between the consecutive time steps is reached.

The solution methodology adopted in the present work is summarized in the flowchart, as shown in Fig. 3.

Fig. 3

Methodology flowchart

The schematic of the blade and the surroundings are shown in Fig. 4.

Fig. 4

Schematic of the blade domain

3 Results and Discussions

When the water droplet hits the surface of the blade, it creates a shockwave that travels at the speed of sound inside the water droplet. The incoming shockwave when breaks, creates a pressure that is more than the water hammer pressure due to the lateral jetting. The pressure at the interface has a different value when compared to the pressure at inside the droplet. As the time progresses, wave propagates into the droplet while varying the pressure inside it. This can be seen in Fig. 5a, b.

Fig. 5

Pressure distributions inside the liquid droplet at different time steps for the impact velocities of 10 m/s (a) and 100 m/s (b) for the nonlinear wave model

The peak pressures obtained for rigid impacts at two different velocities, namely 10 m/s and 100 m/s are compared with the work of Li et al. [4] and the corresponding plots are shown in Figs. 6 and 7, respectively.

Fig. 6

Change in non-dimensional pressure with respect to the time at the interface for the impact velocity of 10 m/s obtained from a nonlinear wave model

Fig. 7

Change in non-dimensional pressure with respect to the time at the interface for the impact velocity of 100 m/s obtained from a nonlinear wave model

Figure 8a, b shows the variation of the pressures and stresses against time on the interface for all the models for the impact velocities of 10 m/s and 100 m/s, respectively

Fig. 8

Variation of impact pressure and stress on the interface w.r.t time period for the impact velocity of 10 m/s (a) and 100 m/s (b)

From Fig. 8a, b, it is seen that all the peak pressures for the linear model are lower than that of the nonlinear model. This can be attributed to the fact that in the nonlinear model, the compressibility of the liquid causes the liquid to get harder which intern induces higher pressure onto the surface of the blade. All the peak pressures on the interface of the blade are higher for the rigid blade when compared to the elastic blade as the blade gets deformed with a deformation speed v_s which cushions the relative velocity of impact which leads to lower pressure action on the surface.

The peak pressure occurs at the time period of 0.2 nanoseconds at the interface and then decreases in an ever-damping wave pattern as shown in Figs. 4 and 5. This phenomenon is also seen in the finding of Marzbali [5].

The effect of erosion has also seemed to have increased with increase in the impact velocity in the experimental results done by Ahmad [2] and numerical results obtained by Chidambaram [3].

By comparing the steady state pressures from Tables 2 and 3, it can be said that as the impact velocity increases, the effect of nonlinearity also increases as the liquid compression is greater with a higher impact speed. The peak pressure ratio between the nonlinear and linear models for rigid model at 10 m/s impact speed is 1.040 and for the 100 m/s of impact speed is 1.150. The same for elastic model at 10 m/s of impact speed is 1.0357; whereas, for 100 m/s of impact speed, the ratio turns out to be 1.1487. In both rigid and elastic model, it is seen that the ratio of pressures is greater in the impact speeds of 100 m/s when compared to 10 m/s.

Table 2 Results of the linear solid–liquid impact model

Table 3 Results of the nonlinear solid–liquid impact model

At higher impact speeds, the pressure at the interface is higher which causes the deformation velocity to increase making the blade’s elasticity become more significant. From Table 2, it is observed that for the nonlinear model, at an impact velocity 10 m/s, the ratio between the deformation velocity v_s and the impact velocity v₀ (v_s/v₀) = 0.0438 and at 100 m/s, the ratio turns out to be 0.04547. This proves that the deformation effect is higher at higher impact speeds.

Coated blade. Figure 9a, b shows the results of the non-dimensional pressure and stress progression with respect to time for the metal coated elastic blade with the Young’s modulus of 100 GPa [8].

Fig. 9

Pressure and stress variations w.r.t time period for the coated blade with Young’s modulus of 100 GPa for impact speeds of 10 m/s (a) and 100 m/s (b)

It can be seen that the peak pressure and peak stress at the interface for the coated blade surface are lower than that of the uncoated blade surface. Young’s modulus of the coated surface changes the elasticity of the blade surface which in turn changes the amount of deformation that occurs in it. This causes the relative impact velocity to be lowered even further which causes the decrease in peak pressure and stress at the surface of the blade.

As seen in Table 4, the variation in both pressure and stress is higher for the higher impact speeds. This is because the property of elasticity highly affects the pressure and with the increase in velocity, the pressure difference is much higher as the deformation speed is more for lower Young’s modulus material.

Table 4 Percentage change in pressure and stress in all scenarios for coated blade

4 Conclusions

In this work, the one-dimensional numerical simulation of erosion of the steam turbine blade due to the condensed water droplets is carried out. For this, a nonlinear acoustic wave equation for the liquid phase is coupled with the elastic solid wave equation for solid phase. Since the viscous forces is insignificantly less, its effect is completely ignored. The key observations made during this work are as follows.

• 1. The nonlinear wave model has a high-steady state and peak pressures which signifies the importance of the nonlinear property which is the variation of speed of sound.

• 2. This work also simulates the shockwave travel inside the droplet while also showing that the elasticity of the solid affects the pressure and stress acted in the liquid droplet and the solid, respectively.

• 3. The analysis is done on the 1Cr13 material turbine blade and a coated turbine blade there by comparing these two results to accurately show the significance of erosion resistance coating onto the blade. This work mainly focuses on the pressure inside the water droplet and the stress induced due to that pressure on the turbine blade while changing the droplet impact speed.

• 4. This work also proves that the impact velocity plays a major role in determining the impact pressure of the water droplet onto the surface of the blade.