Keywords

1 Instruction

China Beidou-3 Global Satellite Navigation System and Galileo Satellite Navigation System have been launched and broadcast penta-frequency signals. Rich GNSS satellite signals have been applied to large-scale and long-distance high-precision fast baseline solution, which has brought new theoretical methods and technical ideas to the near sea positioning of the vast mountainous areas in the West and the coastal areas in the East and the wide area high-precision positioning of provincial administrative regions. At present, BDS-3 broadcasts B1C (1575.42 MHz), B1I (1561.098 MHz), B3I (1268.52 MHz), B2a (1176.45 MHz), B2b (1207.14 MHz) [1, 2]. The increase of observation frequencies number means that more combined signals with long wavelength, weak-ionospheric factors and low-noise characteristics can be constructed [3], which can significantly improve the performance of integer ambiguity resolution and positioning performance.

The application of multi-frequency signals combinations was first proposed by Forssell and Jung. The basic principle is the classical geometric-free (GF) method to fix the ambiguities of EWL, WL and narrow lane (NL) step by step according to the difficulty of ambiguities resolution [4, 5]. This method ignores the influence of ionospheric delay, so it is only suitable for short baseline. In the follow-up, some scholars studied the GF integer combination coefficient to reduce the influence of ionosphere [6], the GF ionospheric-free (IF) linear combination of EWL and NL combinations [7, 8], the ERTK with IF smoothed EWL observations [9], and the optimal GIF combination [10]. Due to the influence of observation noise and unmodeled errors, the ambiguity of NL combinations is difficult to fix in long-baseline in a single epoch, and it takes a long time to smooth to obtain stable and reliable results.

Although it is difficult to reliably fix the ambiguity of NL under the condition of long-baseline, if the observation values of EWL / WL that are easy to be fixed can be fully utilized, the positioning accuracy of decimetre-level can also be obtained, and the positioning performance can be greatly improved compared with the pseudo range observation values [11]. For penta-frequency signals, literature [12] studies the observation values of NL combinations with IR characteristics, which can obtain better noise than the traditional IF combination; On this basis, literature [2] continues to analyze the optimal IR combinations of BDS-3. Aiming at the BDS-3 system, this paper studies the optimal GF combinations and optimal geometric-based (GB) combination of the EWL with weak-ionospheric factors, and uses the fixed optimal IR EWL combination to restrict the IR WL by using GB model. Ignoring the ionospheric parameters, the positioning performance is analyzed and compared with the conventional ionospheric-estimation model to realize the decimetre-level positioning, of which the number of multi-frequency GNSS parameters is minimum, and suitable to apply to long-baseline RTK Positioning.

2 Penta-Frequency Observation Combination Model of BDS-3

2.1 Double Difference (DD) Mathematical Model of BDS-3

The observation equation of the basic pseudo-range and carrier-phase observations is:

$$ \left\{ {\begin{array}{*{20}l} {\Delta \nabla P_{i} = \Delta \nabla \rho + \eta_{i} \Delta \nabla I_{1} + \Delta \nabla T + \Delta \nabla \varepsilon_{P} } \hfill \\ {\Delta \nabla \phi_{i} = \Delta \nabla \rho - \eta_{i} \Delta \nabla I_{1} + \Delta \nabla T + \lambda_{i} \Delta \nabla N_{i} + \Delta \nabla \varepsilon_{\phi } } \hfill \\ \end{array} } \right. $$
(1)

where, the symbol “\(\Delta \nabla\)” represents DD operation; \(P_{i}\) and \(\phi_{i}\) represent pseudo range and carrier observations, respectively; \(\rho\) is the geometric distance between the satellite and the receiver; \(I_{1}\) is the first-order ionospheric delay at the first frequency; \(\eta_{i}\) is the first order ionospheric factor; \(T\) indicates tropospheric delay; \(\varepsilon_{P}\) and \(\varepsilon_{\phi }\) are observation noise of pseudo-range and carrier-phase respectively; \(N\) indicates integer ambiguity; \(\lambda\) is the carrier wavelength.

Correspondingly, the DD observation equation of the penta-frequency signals after basic observation equation linear combination is:

$$ \begin{aligned}\Delta \nabla \phi_{{\left( {i,j,k,m,n} \right)}} \, = &\,\Delta \nabla \rho \, - \,\eta_{{\left( {i,j,k,m,n} \right)}} \,\Delta \nabla I_{1} \, + \,\Delta \nabla T\, + \,\lambda_{{\left( {i,j,k,m,n} \right)}} \,\Delta \nabla N_{{\left( {i,j,k,m,n} \right)}} \\ &+ \,\Delta \nabla \varepsilon_{\phi (i,j,k,m,n)}\end{aligned} $$
(2)

where, each parameter is expressed as:

$$ \Delta \nabla \phi_{{\left( {i,j,k,m,n} \right)}} = \frac{{i \cdot f_{1} \cdot \Delta \nabla \phi_{1} + j \cdot f_{2} \cdot \Delta \nabla \phi_{2} + k \cdot f_{3} \cdot \Delta \nabla \phi_{3} + m \cdot f_{4} \cdot \Delta \nabla \phi_{4} + n \cdot f_{5} }}{{i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} + m \cdot f_{4} + n \cdot f_{5} }} $$
(3)
$$ \eta_{{\left( {i,j,k,m,n} \right)}} = \frac{{f_{1}^{2} \left( {{i \mathord{\left/ {\vphantom {i {f_{1} }}} \right. \kern-\nulldelimiterspace} {f_{1} }} + {j \mathord{\left/ {\vphantom {j f}} \right. \kern-\nulldelimiterspace} f}_{2} + {k \mathord{\left/ {\vphantom {k {f_{3} }}} \right. \kern-\nulldelimiterspace} {f_{3} }} + {m \mathord{\left/ {\vphantom {m {f_{4} }}} \right. \kern-\nulldelimiterspace} {f_{4} }} + {n \mathord{\left/ {\vphantom {n {f_{5} }}} \right. \kern-\nulldelimiterspace} {f_{5} }}} \right)}}{{i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} + m \cdot f_{4} + n \cdot f_{5} }} $$
(4)
$$ \lambda_{{\left( {i,j,k,m,n} \right)}} = \frac{c}{{i \cdot f_{1} + j \cdot f_{2} + k \cdot f_{3} + m \cdot f_{4} + n \cdot f_{5} }} $$
(5)
$$ \mu_{{\left( {i,j,k,m,n} \right)}} = \frac{{\sqrt {(if_{1} )^{2} + (jf_{2} )^{2} + (kf_{3} )^{2} + (mf_{4} )^{2} + (nf_{5} )^{2} } }}{{f_{{\left( {i,j,k,m,n} \right)}} }} $$
(6)

where, \(i,j,k,m,n\) is the combination coefficient; Correspondingly, the calculation of pseudo range combination \(\Delta \nabla P_{{\left( {i,j,k,m,n} \right)}}\) is similar to that of \(\Delta \nabla \phi_{{\left( {i,j,k,m,n} \right)}}\); \(\lambda_{{\left( {i,j,k,m,n} \right)}}\) is the wavelength of combined observations; \(\mu_{{\left( {i,j,k,m,n} \right)}}\) is the noise coefficient of combined observations; \(c\) is the speed of light.

2.2 Selection of Optimal GF-IR EWL Combination

The combination of penta-frequency EWL combination can construct infinite combined observations according to different coefficient values, but most signals do not have the characteristics of low-noise and weak-ionospheric factor. Referring to literature [2], this paper selects the IR EWL/WL for long-baseline positioning, and makes the following constraints on the characteristics of combined observations:

  1. (1)

    The influence of ionospheric delay on ambiguity resolution is less than 0.02 cycles in unit, which can be expressed as:

    $$ \beta_{{\left( {i,j,k,m,n} \right)}} = \frac{{f_{1}^{2} \left( {{i \mathord{\left/ {\vphantom {i {f_{1} }}} \right. \kern-\nulldelimiterspace} {f_{1} }} + {j \mathord{\left/ {\vphantom {j f}} \right. \kern-\nulldelimiterspace} f}_{2} + {k \mathord{\left/ {\vphantom {k {f_{3} }}} \right. \kern-\nulldelimiterspace} {f_{3} }} + {m \mathord{\left/ {\vphantom {m {f_{4} }}} \right. \kern-\nulldelimiterspace} {f_{4} }} + {n \mathord{\left/ {\vphantom {n {f_{5} }}} \right. \kern-\nulldelimiterspace} {f_{5} }}} \right)}}{c} $$
    (7)

    The ionospheric delay corresponding to 5 m has less than 0.1 cycles on ambiguity resolution. If the impact on ranging is less than 5 cm, it is required.

  2. (2)

    If the combined noise is required to be small, the combined coefficient of the combination value should not be too large. Taking the GPS EWL combination (1, 6, −5) as the reference (103.80), the noise amplification coefficient shall not be greater than 110;

  3. (3)

    The wavelength of the combined observation value shall not be too small or too large. The combination wavelength shall be between 0.8 m and 10 m with reference of GPS triple-frequency WL combination the twice (1, −1, 0) and (0, 1, −1).

Based on the above three conditions, take [−10, 10] as the search interval of combination coefficient, the characteristics of combinations meeting the above conditions are shown in Table 1. The sequence of corresponding BDS-3 signal types in the Table 1 is: B1C/B1I/B3I/B2a/B2b. It can be seen from the table that there are four EWL/WL combinations of BDS-3 that meet the conditions, of which (−1, 2, −4, 1, 2) is EWL combination and the rest are WL combinations. Therefore (−1, 2, −4, 1, 2) of BDS-3 is selected as the optimal IR EWL combination.

Table 1. Ionosphere-reduced WL combinations for BDS-3
Full size table

Equation (8) calculates the IR WL by using the combination of GIF:

$$ \Delta \nabla N_{{\left( {i,j,k,m,n} \right)}} = \left[ {\frac{{\Delta \nabla P_{[a,b,c,d,e]} - \Delta \nabla \phi_{{\left( {i,j,k,m,n} \right)}} }}{{\lambda_{{\left( {i,j,k,m,n} \right)}} }}} \right] $$
(8)
$$ \Delta \nabla P_{[a,b,c,d,e]} = a\Delta \nabla P_{1} + b\Delta \nabla P_{2} + c\Delta \nabla P_{3} + d\Delta \nabla P_{4} + e\Delta \nabla P_{5} $$
(9)

where, \(\left[ \bullet \right]\) represents the rounding operator, \(\Delta \nabla P_{[a,b,c,d,e]}\) is the linear combination form of DD observations of pseudo-range combination, and the combination coefficient of pseudo-range \(a,b,c,d,e\) is any real number. As shown in Eq. (10)–(12), considering that the sum of pseudo-range coefficients is 1, the sum of ionospheric factor of combined pseudo-range observations and IR is 0, and the combined noise is the smallest, the optimal pseudo-range coefficient can be calculated by the minimum norm method in literature [13], as shown in Table 2.

$$ a + b + c + d + e = 1 $$
(10)
$$ \beta_{{\left( {i,j,k,m,n} \right)}} + a + b \cdot \frac{{f_{1}^{2} }}{{f_{2}^{2} }} + c \cdot \frac{{f_{1}^{2} }}{{f_{3}^{2} }} + d \cdot \frac{{f_{1}^{2} }}{{f_{4}^{2} }} + e \cdot \frac{{f_{1}^{2} }}{{f_{5}^{2} }} = 0 $$
(11)
$$ a^{2} + b^{2} + c^{2} + d^{2} + e^{2} = \min $$
(12)
(13)

where, \(\sigma_{\Delta \nabla \phi }\) and \(\sigma_{\Delta \nabla P}\) represent the DD noise of non-combined carrier observation value and pseudo-range observation respectively, and the values in this paper are 0.5 m and 5 mm respectively.

The optimal pseudo-range coefficient combination of each IR combination is brought into respectively, and the rounding success rate of ambiguities of IR WL \(P_{s}\) is calculated by Eq. (14).

$$ P_{s} \left( { - 0.5{\rm{ < }}x{\rm{ < 0}}{\rm{.5}}} \right) = \int_{ - 0.5}^{0.5} {\frac{1}{{\sigma \sqrt {2\pi } }}} \exp \left( { - \frac{{\left( {x - \delta } \right)^{2} }}{{2\sigma^{2} }}} \right)dx $$
(14)

where, \(\delta\) is the systematic deviation caused by unmodeled errors. When calculating the ambiguities of GIF EWL combinations, the first-order ionospheric delay, tropospheric delay and satellite orbit error are eliminated. Therefore, the ambiguity accuracy is only affected by observation noise and second-order ionospheric delay. Here, the influence of second-order ionospheric delay can be ignored, so it can be regarded as 0.

Table 2. Optimal combination of pseudo-range coefficients of ionosphere-reduced WL combinations and success rate by rounding
Full size table

It can be seen from Table 2 that the (−1, 2, −4, 1, 2) combination can obtain a rounding success rate of 100%. Therefore, the (−1, 2, −4, 1, 2) combination is only affected by pseudo-range noise, and under the condition of good observation accuracy IR EWL can be fixed by rounding in a single epoch.

2.3 Selection of EWL/WL in Optimal GB-IR

The selection of IR EWL based on geometry can make full use of pseudo-range observation data. Referring to literature [14], using the estimated ionosphere model to calculate EWL combinations. The corresponding model is:

$$ A = \left[ {\begin{array}{*{20}l} 1 \hfill & {\eta_{1} } \hfill & 0 \hfill \\ 1 \hfill & {\eta_{2} } \hfill & 0 \hfill \\ 1 \hfill & {\eta_{3} } \hfill & 0 \hfill \\ 1 \hfill & {\eta_{4} } \hfill & 0 \hfill \\ 1 \hfill & {\eta_{5} } \hfill & 0 \hfill \\ 1 \hfill & { - \eta_{EWL} } \hfill & {\lambda_{EWL} } \hfill \\ \end{array} } \right] $$
(15)
$$ R = \left[ {\begin{array}{*{20}l} {\sigma_{P}^{2} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {\sigma_{P}^{2} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {\sigma_{P}^{2} } \hfill & {} \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {\sigma_{P}^{2} } \hfill & {} \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\sigma_{P}^{2} } \hfill & {} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\sigma_{EWL}^{2} } \hfill \\ \end{array} } \right] $$
(16)
$$ P = R^{ - 1} $$
(17)
$$ Q = \left( {A^{T} PA} \right)^{ - 1} $$
(18)

where, \(A\) is the design matrix, and the corresponding estimation parameters are station satellite distance accuracy, ionospheric accuracy and ambiguity accuracy; \(R\) is the corresponding observation noise variance covariance matrix; \(\sigma_{EWL}^{2} = \eta_{EWL}^{2} \sigma_{\phi }^{2}\) is the observation noise of EWL; The matrix \(Q\) is the variance covariance matrix of parameter estimation, which reflects the accuracy of parameter estimation, and its diagonal element is the variance of estimated parameters. The IR EWL is affected by the unmodeled atmospheric residual and orbit error when GB model used. Specifically, \(\delta\) in Eq. (14) can be calculated by Eq. (19):

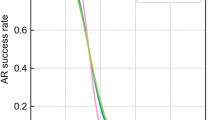
$$ \delta = \frac{{\Delta \nabla orb + \Delta \nabla T - \eta_{{\left( {i,j,k,m.n} \right)}} \Delta \nabla I}}{{\lambda_{{\left( {i,j,k,m.n} \right)}} }} $$
(19)

Referring to literature [6], it is assumed that under the conditions of medium and long-baseline, the tropospheric residuals are 10 cm and 15 cm respectively, and the first-order ionospheric residuals are 80 cm and 100 cm respectively. The corresponding ambiguity accuracy and success rate are shown in Table 3.

Table 3. BDS-3 optimal GB-IR ambiguity accuracy and success rate by rounding
Full size table

Regarding of estimating the ionospheric delay, the GB model reduces the ambiguity intensity, which is equivalent to the ionosphere-fixed model [15]. Although the BDS-3 IR combination (−1, 2, −4, 1, 2) cannot obtain 100% success rate by using GB model, if four linearly independent EWL combinations are found, the ambiguities of IR EWL can be obtained by linear combination. Unfortunately, only three groups of linearly independent EWL with high ambiguity accuracy can be obtained. Therefore, The linear combination method is not suitable to provide the success rate of IR EWL.

2.4 Selection of Calculation Model for EWL / WL

Therefore, the IR EWL can be obtained directly by rounding using GF model.

In this paper, the IR EWL of BDS-3 is calculated by GF method. As a comparison, with reference to Eq. (20), which estimates ionospheric parameters with low-noise EWL combinations:

$$ \left[ {\begin{array}{*{20}c} {{\varvec{v}}_{{P_{1} }} } \\ {{\varvec{v}}_{{P_{2} }} } \\ {{\varvec{v}}_{{P_{3} }} } \\ {{\varvec{v}}_{{P_{4} }} } \\ {{\varvec{v}}_{{P_{5} }} } \\ {{\varvec{v}}_{EWL} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}l} {\varvec{B}} \hfill & {\eta_{1} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & {\eta_{2} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & {\eta_{3} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & {\eta_{4} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & {\eta_{5} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & { - \eta_{EWL} {\varvec{I}}_{s} } \hfill & {\lambda_{EWL} {\varvec{I}}_{s} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{x}} \\ {{\varvec{ion}}} \\ {{\varvec{N}}_{EWL} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {{\varvec{l}}_{{P_{1} }} } \hfill \\ {{\varvec{l}}_{{P_{2} }} } \hfill \\ {{\varvec{l}}_{{P_{3} }} } \hfill \\ {{\varvec{l}}_{{P_{4} }} } \hfill \\ {{\varvec{l}}_{{P_{5} }} } \hfill \\ {{\varvec{l}}_{EWL} } \hfill \\ \end{array} } \right] $$
(20)

After fixing EWL, the calculation of WL ambiguity is selected according to its combination characteristics. Generally, the fixed EWL combinations are used to restrict the ambiguity of WL combinations, as shown in Eq. (21).

$$ \left[ {\begin{array}{*{20}c} {{\varvec{v}}_{EWL}^{^{\prime}} } \\ {{\varvec{v}}_{WL} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}l} {\varvec{B}} \hfill & { - \eta_{EWL} {\varvec{I}}_{s} } \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & { - \eta_{WL} {\varvec{I}}_{s} } \hfill & {\lambda_{WL} {\varvec{I}}_{s} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{x}} \\ {{\varvec{ion}}} \\ {{\varvec{N}}_{WL} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {{\varvec{l}}_{EWL}^{^{\prime}} } \hfill \\ {{\varvec{l}}_{WL} } \hfill \\ \end{array} } \right] $$
(21)

The WL is constrained by IR EWL, and ionosphere can be ignored because it is very little. Its estimation equation is:

$$ \left[ {\begin{array}{*{20}c} {{\varvec{v}}_{EWL}^{^{\prime}} } \\ {{\varvec{v}}_{WL} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}l} {\varvec{B}} \hfill & {\varvec{0}} \hfill \\ {\varvec{B}} \hfill & {\lambda_{WL} {\varvec{I}}_{s} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{x}} \\ {{\varvec{N}}_{WL} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {{\varvec{l}}_{EWL}^{^{\prime}} } \hfill \\ {{\varvec{l}}_{WL} } \hfill \\ \end{array} } \right] $$
(22)

It can be seen that using the IR EWL to restrict the IR WL does not need to estimate the ionospheric parameters, and the dimension of parameter estimation can be reduced.

3 Experiment and Analysis

In this paper, a group of 189.4 km long-baseline of IGS station are used for the experiment. The data comes from TIT2 and FFMJ stations of BKG data center. The observation date is UTC time, October 1, 2021 (24 h), day of year is 274, and the sampling interval is 30. During the calculation, the cut-off angle of the satellite in the calculation is set to 20°.

The number of BDS-3 satellites with five frequencies and their RDOP in this period are shown in Fig. 1. The number of common view satellites of the two stations fluctuates in the range of 4–7. The corresponding RDOP value fluctuates greatly when the number of satellites is 4. Therefore, it is required to solve when the number of satellites is greater than 4. Figure 2 shows the sky plots of BDS-3 various satellites in the experiment.

Fig. 1.
figure 1

Number of satellites and RDOP value of BDS-3 in full time

Full size image
Fig. 2.
figure 2

Sky plots for the various satellites of BDS-3

Full size image

Figure 3 shows the fractions of EWL combinations ambiguities using ionospheric estimation model. Different colors correspond to different satellite pairs. It can be seen that the ionospheric estimation model can be all within 0.25 weeks and can be reliably rounded and fixed.

Fig. 3.
figure 3

The fractions of EWL of the ionospheric float model

Full size image

The WL ambiguity is calculated by ionospheric estimation model and the suboptimal/optimal ambiguity variance ratio (Ratio value) is shown in Fig. 4. In the figure, the values corresponding to the red lines in the upper and lower figures are 10 and 2.5 respectively. It can be seen that at 1800 epoch, the Ratio value is relatively low because the number of satellites is small and the RDOP value is relatively low. At 250 epoch, 1200 epoch, 1400 epoch, 1750 epoch, 2000 epoch and 2200 epoch, only 4 satellites are available, resulting in poor geometry and unstable positioning accuracy, so they are eliminated.

Fig. 4.
figure 4

The Ratio of WL ambiguity

Full size image
Fig. 5.
figure 5

Positioning error with EWL/WL

Full size image

After the WL ambiguities are fixed, the observation equations are brought back to obtain the coordinate solution under the fixed solution. The positioning error of the corresponding solution coordinates in the East (E), North (N) and sky (U) directions is shown in Fig. 5.

Finally, the positioning accuracy statistics of the two methods are shown in Table 4. It can be seen that the accuracy of the IR method is lower than that of the ionospheric estimation method, which is consistent with the theoretical derivation. However, the IR does not need to estimate the ionospheric delay term, so it can achieve higher ambiguity calculation efficiency. Especially in the multi-level step-by-step solution of multi-system ambiguity, it will be more obvious.

Table 4. Statistics of the positioning results with EWL/WL observations
Full size table

4 Conclusions

In this paper, a step-by-step method for fixing the ambiguities of IR EWL/WL combinations is proposed. Firstly, the optimal pseudo-range GF method is used to solve the ambiguities of IR EWL combinations, and then the fixed observation values of EWL combinations are used to constrain the WL combinations. This method does not need to estimate the ionospheric delay when calculating the ambiguities of WL, and can reduce the time required for de correlation of LAMBDA algorithm.

Although the positioning accuracy is lower than that using the ionosphere estimation method, the positioning results at the decimeter level in a single epoch can still be achieved.