Keywords

1 Introduction

Functionally graded materials (FGMs) are a class of composites, introduced by Japanese scientists in 1984 as high temperature resistant materials (Yamanoushi et al. 1990) for aircraft and space vehicles.

These materials are microscopically heterogeneous with smooth variation of material properties and are found to have immense applications in aircraft, mechanical, nuclear and biomechanical structures. Hence these materials needs to be modeled properly and their behavior should be studied carefully. Two types of representations are widely followed in the literature to describe the properties of FGMs viz., power-law and exponential law. Studies on these materials available in literature mainly revolve around materials with power-law variation of properties while much attention was not given to exponentially graded plates. Therefore the present study concerns about the cylindrical bending and vibrations of exponentially graded plates under plane strain conditions.

Srinivas et al. (1970) have provided analytical solutions for free vibration of isotropic and laminated plates using three dimensional (3D) elasticity theory. Qian et al. (2004) have studied the static, free and forced vibrations of thick rectangular functionally graded (FG) plates using a higher order shear normal deformation theory and a meshless local Petrov–Galerkin method. While an alternate meshless point collocation method and third order shear deformation is used by Ferreira et al. (2005) in their study of FG plate static analysis. In plane and out of plane frequencies of FG circular and annular plates were given by Hosseini-Hashemi et al. (2010a) based on Mindlin’s first order shear deformation theory (FOST). Shear correction factor of 5/6 used for homogeneous plates was found to give unsatisfactory results for higher mode frequencies of FG plates. Therefore, gradation dependent shear correction factors are used by Hosseini-Hashemi et al. (2010b) in their solution for free vibration of rectangular FGM plates resting on elastic foundations. These gradation dependent shear correction factors have considerably improved the solution. Gradation dependent shear correction factors are also used by Nguyen et al. (2008) while studying the behavior a simply supported FG plate and a clamped sandwich plate with FG faces in cylindrical bending. An exact solution for cylindrical bending of functionally graded piezoelectric laminates has been provided by Lu et al. (2005). Response of the plate under mechanical and electric loading is studied using Stroh formalism and benchmark results are established. Zenkour (2005), using sinusoidal shear deformation theory studied the free vibrations and buckling of simply supported functionally graded plates. Rotary inertia is considered with power law variation of material properties. Cheng and Batra (2000) have provided closed form solution for the thermomechanical deformations of elliptic functionally graded plates with clamped boundary conditions. The deformation of the plate due to thermal load is calculated analytically and those due to mechanical loads are calculated by the method of asymptotic expansion. Reddy and Cheng (2001) have studied 3D thermomechanical deformations of functionally graded simply supported plates using the method of asymptotic expansion. Vel and Batra (2002) have presented exact solution for cylindrical bending vibration of FG plates with power law variation of material properties. Plane strain condition is assumed in the study. Power series method has been utilized and the effective properties at a point were estimated by Mori–Tanaka and self-consistent homogenization schemes. The same formulation has been extended by Vel and Batra (2004) to find the 3D exact solution for free and forced vibrations of FG simply supported plates. Chen (2005) considered the nonlinear vibration of initially stressed, shear deformable FG plate using Galerkin method and FOST.

The power series formulation adopted by Vel and Batra (2004) has been used in the present work to provide exact natural frequencies of exponentially graded plates in cylindrical bending. Plane strain assumption has been employed to reduce the 3D elasticity problem to a two dimensional (2D) problem. 2D elasticity equations are solved exactly using Navier’s technique and displacements in the thickness direction are expanded using power series.

2 Theoretical Formulation

2.1 Exponentially Graded Material Properties

Elastic modulus and mass density of an exponentially graded plate can be represented by,

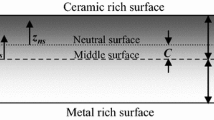
$$ {\text{E}}\left( {\text{z}} \right) = {\text{E}}_{{\text{b}}} \;e^{{p\left( {\frac{z}{h} + \frac{1}{2}} \right)}} ,\quad {\text{E}}_{{\text{t}}} = {\text{E}}_{{\text{b}}} \;e^{p} ,\quad p \ne 0 $$
$$ \rho \left( {\text{z}} \right) = \rho_{{\text{b}}} \; e^{{p\left( { \frac{z}{h} + \frac{1}{2} } \right)}} ,\quad \rho_{{\text{t}}} = \rho_{{\text{b}}} e^{p} ,\quad p \ne 0 $$

where, ‘p’ is an index of exponential variation and for p = 0, the material becomes homogeneous. Variation of material property across the thickness is shown in Fig. 1.

Fig. 1
figure 1

Typical normalized material property variation across the thickness of the plate

Full size image

2.2 Governing Equations of Motion

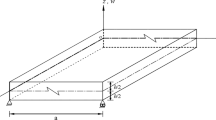
A rectangular plate with dimensions a, b, h along x, y and z axes, respectively is considered. Figure 2 shows the geometry of the plate with positive set of coordinate axes.

Fig. 2
figure 2

Rectangular plate with positive set of reference axes

Full size image

Under plane strain conditions (i.e., as \({\text{y}}\, \to \infty\)), the plate in Fig. 2 can be idealized as the one shown in Fig. 3 with unit width in y-direction. The governing equations of motion of the plate are given by,

$$ \begin{gathered} \frac{{\partial \sigma_{{\text{x}}} }}{{\partial {\text{x}}}} + \frac{{\partial \tau_{{{\text{zx}}}} }}{{\partial {\text{z}}}} = \rho \left( {\text{z}} \right) \frac{{\partial^{2} {\text{u}}}}{{\partial t^{2} }} \hfill \\ \frac{{\partial \sigma_{z} }}{{\partial {\text{z}}}} + \frac{{\partial \tau_{{{\text{xz}}}} }}{{\partial {\text{x}}}} = \rho \left( {\text{z}} \right) \frac{{\partial^{2} {\text{w}}}}{{\partial t^{2} }} \hfill \\ \end{gathered} $$
(1)
Fig. 3
figure 3

Plate in plane strain condition with unit width

Full size image

The strains in the plate under 3D state of stress are given by,

$$ \begin{gathered} \varepsilon_{x} = \frac{{\sigma_{x} }}{E\left( z \right)} - \nu \frac{{\sigma_{y} }}{E\left( z \right)} - \nu \frac{{\sigma_{z} }}{E\left( z \right)};\quad \varepsilon_{y} = - \nu \frac{{\sigma_{x} }}{E\left( z \right)} + \frac{{\sigma_{y} }}{E\left( z \right)} - \nu \frac{{\sigma_{z} }}{E\left( z \right)}; \hfill \\ \varepsilon_{z} = - \nu \frac{{\sigma_{x} }}{E\left( z \right)} - \nu \frac{{\sigma_{y} }}{E\left( z \right)} + \frac{{\sigma_{z} }}{E\left( z \right)}; \hfill \\ \gamma_{xz} = G\left( z \right) \tau_{xz} ;\quad \gamma_{xy} = G\left( z \right) \tau_{xy} ;\quad \gamma_{yz} = G\left( z \right) \tau_{yz} \hfill \\ \end{gathered} $$
(2)

But, for a plate in cylindrical bending (plane strain condition), we have,

$$ \varepsilon_{y} \approx 0 ; \gamma_{xy} \approx 0 ; \gamma_{yz} \approx 0 $$
(3)

Now, from Eq. (3), stress–strain relations in Eq. (2) can be rewritten for a plane strain case as,

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{z} } \\ {\tau_{xz} } \\ \end{array} } \right\} = \frac{E\left( z \right)}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\begin{array}{*{20}c} {1 - \nu \nu 0} \\ {\nu 1 - \nu 0} \\ { 0 0 0.5 - \nu } \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{z} } \\ {\gamma_{xz} } \\ \end{array} } \right\} $$
(4)

Strain–Displacement relations, assuming small deformations, are given by,

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{z} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ {\frac{\partial w}{{\partial z}}} \\ {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \\ \end{array} } \right\} $$
(5)

Now, from Eqs. (4) and (5), equations of motion in (1) can be written in terms of displacements as,

$$ \begin{gathered} E\left( z \right)\left( {1 - {\upnu }} \right)\frac{{\partial^{2} {\text{u}}}}{{\partial x^{2} }} + E\left( z \right)\left( {0.5 - {\upnu }} \right)\frac{{\partial^{2} {\text{u}}}}{{\partial z^{2} }} + 0.5 E\left( z \right)\frac{{\partial^{2} {\text{w}}}}{\partial x\partial z} \hfill \\ \quad \quad \quad + \left( {0.5 - {\upnu }} \right)\left\{ { \frac{{\partial {\text{u}}}}{{\partial {\text{z}}}}{ + }} \right.\left. {\frac{{\partial {\text{w}}}}{{\partial {\text{x}}}} } \right\}\frac{{\partial {\text{E(z)}}}}{{\partial {\text{z}}}} { = }\frac{\rho \left( z \right)}{C}{ }\frac{{\partial^{2} {\text{u}}}}{{\partial t^{2} }} \hfill \\ E\left( z \right)\left( {1 - {\upnu }} \right)\frac{{\partial^{2} {\text{w}}}}{{\partial z^{2} }} + E\left( z \right)\left( {0.5 - {\upnu }} \right)\frac{{\partial^{2} {\text{w}}}}{{\partial x^{2} }} + 0.5 E\left( z \right)\frac{{\partial^{2} {\text{u}}}}{\partial x\partial z} \hfill \\ \quad \quad \quad + \left\{ {\nu \frac{{\partial {\text{u}}}}{{\partial {\text{x}}}}} \right.\left. { + (1 - {\nu )}\frac{{\partial {\text{w}}}}{{\partial {\text{z}}}} } \right\}\frac{{\partial {\text{E(z)}}}}{{\partial {\text{z}}}} { = }\frac{\rho \left( z \right)}{C}{ }\frac{{\partial^{2} {\text{w}}}}{{\partial t^{2} }} \hfill \\ \end{gathered} $$
(6)

Solution of these coupled differential equations (6) with variable coefficients is systematically explained in the next section. Simply (diaphragm) supported boundary conditions given by the following equations are considered in the present study.

$$ {\text{At x}} = 0{\text{ and x}} = {\text{a}}; \sigma_{x} = 0 ;w = 0 $$
(7)

3 Exact Solution

The solution for displacement field which satisfies Eq. (7) can be assumed in the form of,

$$ \begin{gathered} u\left( {x,z,t} \right) = h\sum\limits_{m = 0}^{\infty } {\sum\limits_{r = 0}^{\infty } {A_{r } \left( \frac{2z}{h} \right)^{r} \cos \left( {\frac{m\pi x}{a}} \right)e^{i\omega t} } } \hfill \\ w\left( {x,z,t} \right) = h\sum\limits_{m = 0}^{\infty } {\sum\limits_{r = 0}^{\infty } {C_{r } \left( \frac{2z}{h} \right)^{r} \sin \left( {\frac{m\pi x}{a}} \right)e^{i\omega t} } } \hfill \\ \end{gathered} $$
(8)

Substituting Eq. (8) into Eq. (6) and also using the orthogonality relations between trigonometric functions, we have,

$$ \begin{gathered} \sum\limits_{r = 0}^{\infty } {\left[ {\begin{array}{*{20}c} {\left\{ {E\left( z \right)\left( {\nu - 1} \right)\alpha^{2} + \frac{\rho \left( z \right)}{C}\omega^{2} } \right\}h A_{r} + \frac{4}{h}E\left( z \right)\left( {0.5 - \nu } \right)\left( {r + 1} \right)\left( {r + 2} \right)A_{r + 2} } \\ { + E\left( z \right)\alpha \left( {r + 1} \right)C_{r + 1} + \left( {0.5 - \nu } \right)\frac{\partial E\left( z \right)}{{\partial z}}\left\{ {\alpha hC_{r} + 2\left( {r + 1} \right)A_{r + 1} } \right\}} \\ \end{array} } \right]\left( \frac{2z}{h} \right)^{r} = 0} \hfill \\ \sum\limits_{r = 0}^{\infty } {\left[ {\begin{array}{*{20}c} {\frac{4}{h}E\left( z \right)\left( {1 - \nu } \right)\left( {r + 1} \right)\left( {r + 2} \right)C_{r + 2} + \left\{ {E\left( z \right)\left( {\nu - 0.5} \right)\alpha^{2} + \frac{\rho \left( z \right)}{C}\omega^{2} } \right\}hC_{r} } \\ { - E\left( z \right)\alpha \left( {r + 1} \right)A_{r + 1} + \frac{\partial E\left( z \right)}{{\partial z}}\left\{ { - \nu \alpha hA_{r} + 2\left( {1 - \nu } \right)\left( {r + 1} \right)C_{r + 1} } \right\}} \\ \end{array} } \right]\left( \frac{2z}{h} \right)^{r} = 0} \hfill \\ \end{gathered} $$
(9)

Equation (9) represents the recurrence relationship between coefficients of the power series. These relations can be concisely expressed as,

$$ \left\{ {\begin{array}{*{20}c} {A_{r + 2} } \\ {C_{r + 2} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{{{\text{I}}_{2} }}{{{\text{I}}_{1} }} \frac{{{\text{I}}_{3} }}{{{\text{I}}_{1} }} \frac{{{\text{I}}_{4} }}{{{\text{I}}_{1} }} \frac{{{\text{I}}_{5} }}{{{\text{I}}_{1} }}} \\ {\frac{{{\text{I}}_{7} }}{{{\text{I}}_{6} }} \frac{{{\text{I}}_{8} }}{{{\text{I}}_{6} }} \frac{{{\text{I}}_{9} }}{{{\text{I}}_{6} }} \frac{{{\text{I}}_{10} }}{{{\text{I}}_{6} }}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{r} } \\ {A_{r + 1} } \\ {C_{r} } \\ {C_{r + 1} } \\ \end{array} } \right\} $$
(10)

in which the coefficients of the matrix given by Eq. (10) are given by,

$$ I_{1} = \left\{ {\frac{4}{h} \left( {0.5 - \nu } \right)\left( {r + 1} \right)\left( {r + 2} \right)} \right\};\quad I_{2} = \left\{ {\left( {1 - \nu } \right)\alpha^{2} - \frac{{\rho_{b} }}{{E_{b} }}\frac{{\omega^{2} }}{C}} \right\}h $$
$$ I_{3} = \left\{ { - \frac{2p}{h} \left( {0.5 - \nu } \right)\left( {r + 1} \right)} \right\};\quad I_{4} = \left\{ { - p \left( {0.5 - \nu } \right)\alpha } \right\} $$
$$ I_{5} = - \alpha \left( {r + 1} \right);\quad I_{6} = \left\{ {\frac{4}{h} \left( {1 - \nu } \right)\left( {r + 1} \right)\left( {r + 2} \right)} \right\} $$
$$ I_{7} = p\nu \alpha ;\quad I_{8} = - I_{5} $$
$$ I_{9} = - I_{5} - \left\{ {\left( { - 0.5 + \nu } \right)\left( {\alpha^{2} } \right) + \frac{{\rho_{b} }}{{E_{b} }}\frac{{\omega^{2} }}{C}} \right\}h;\quad I_{10} = \left\{ { - \frac{2p}{h} \left( {1 - \nu } \right)\left( {r + 1} \right)} \right\} $$

Now, the surface boundary conditions for a transversely loaded plate are given by,

$$ \begin{gathered}{\text{At}}\;z = \mp \frac{h}{2}\quad \quad \begin{array}{*{20}c} { \sigma_{z} = q^{z} : \frac{E\left( z \right)}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left\{ {\left( {1 - \nu } \right)\frac{\partial w}{{\partial z}} + \nu \frac{\partial u}{{\partial x}}} \right\} = q^{z} } \\ {\tau_{zx} = 0 : \frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}} = 0} \\ \end{array} \hfill \end{gathered} $$
(11)

where, \(q^{z}\) is the intensity of transverse load in stress units. \(\left( {q^{z} = q^{ + } at z = \frac{h}{2} ; q^{z} = q^{ - } at z = - \frac{h}{2}} \right)\).

Substituting Eq. (8) into Eq. (11), we obtain the boundary conditions given by,

$$ \begin{gathered} {\text{At}}\;z = \frac{h}{2}\quad \quad \begin{array}{*{20}c} {\sum\limits_{r = 0}^{\infty } {\left\{ {2\left( {1 - \nu } \right)\left( {r + 1} \right)C_{r + 1} - \nu \alpha hA_{r} } \right\} = \frac{{q^{ + } }}{{D_{t} }}} } \\ {\sum\limits_{r = 0}^{R} {\left\{ {2\left( {r + 1} \right)A_{r + 1} + h\alpha C_{r} } \right\} = 0} } \\ \end{array} \hfill \\ {\text{At}}\;z = - \frac{h}{2}\quad \quad \begin{array}{*{20}c} {\sum\limits_{r = 0}^{\infty } {\left\{ {\left( {2\left( {1 - \nu } \right)\left( {r + 1} \right)C_{r + 1} - \nu \alpha hA_{r} } \right)\left( { - 1} \right)^{r} } \right\} = \frac{{q^{ - } }}{{D_{b} }}} } \\ {\sum\limits_{r = 0}^{\infty } {\left\{ {\left( {2\left( {r + 1} \right)A_{r + 1} + h\alpha C_{r} } \right)\left( { - 1} \right)^{r} } \right\} = 0} } \\ \end{array} \hfill \\ \end{gathered} $$
(12)

These boundary conditions together with the recurrence relations in Eq. (10), can be written as,

$$ \left[ {{\text{M}}\left( \omega \right)} \right]_{4x4} \left\{ {\begin{array}{*{20}c} {A_{0} } \\ {C_{0} } \\ {A_{1} } \\ {C_{1} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{q^{ + } }}{{D_{t} }}} \\ 0 \\ {\frac{{q^{ - } }}{{D_{b} }}} \\ 0 \\ \end{array} } \right\} $$
(13)

where, elements of matrix ‘M’ contain polynomials in ‘\(\omega\)’. For a plate undergoing free vibrations, there are no tractions on the surfaces (\(q^{ + } = q^{ - } = 0\)). In such a situation, the boundary conditions in Eq. (11) become homogeneous and Eq. (13) define the eigenvalue problem for the natural frequencies of FG plate, the nonzero solution of which requires,

$$ \det ({\text{M}}) = 0 $$
(14)

Equation (14) represents the characteristic polynomial of the eigenvalues. The roots of the polynomial give the natural frequencies of the FG plate.

For the static analysis of FG plates, the recurrence relations in Eq. (10) can be rewritten by substituting ‘\(\omega\)’ equal to zero. Thus obtained recurrence relations together with the non-homogeneous boundary conditions in Eq. (12) can be used to find the coefficients (using Eq. (13)) in the power series from which the displacement field in Eq. (8) can be readily obtained. Stresses and strains can be obtained from the definitions given by Eqs. (4) and (5) respectively.

4 Numerical Results and Discussions

4.1 Natural Frequencies (Free Vibration)

FG plate with different gradations (p) is considered in the study. Flexural mode frequencies are calculated and are given in Table 1. Table 2 compares the frequencies of FG plate computed from the assumption of plane strain to frequencies computed from 3D elasticity theory using the complete set of governing equations and constitutive relationships.

Table 1 Non-dimensional frequencies of FG plate in cylindrical bending for various gradations
Full size table
Table 2 Variation of fundamental frequency \(\lambda_{{\left( {1,1} \right)}}\) of FG plates with aspect ratio (p = 3)
Full size table

Non-dimensional frequency, \(\lambda = \omega h\sqrt {\frac{{\rho_{b} }}{{G_{b} }}}\); = 0.3.

4.2 Stress Analysis of FG Plates in Cylindrical Bending

As static solution for cylindrical bending of FG plates is already available (Zhong et al. 2010), detailed derivations are not presented here. But the extension of present formulation for calculating stresses and deflections is straightforward as explained at the end of Sect. 3. For the static analysis of FG plate in cylindrical bending, the equilibrium equations in (1) can be modified to account for the body forces while discarding the inertia forces. The static equilibrium equations under sinusoidal loading are solved and the results (plane strain) are presented in Table 3. The non-dimensional quantities and loads used in the present plane strain formulation are given below.

$$ q\left( x \right) = q^{ + } = q_{0} \sin \left( {\frac{\pi x}{a}} \right); q^{ - } = 0 ; $$
$$ \overline{w} = w\left( {\frac{a}{2},z} \right) \frac{{100E_{t} h^{3} }}{{q_{0} a^{4} }} ; \overline{\sigma }_{xx} = \sigma_{xx} \left( {\frac{a}{2},z} \right)\frac{{h^{2} }}{{q_{0} a^{2} }} ; \overline{\tau }_{xz} = \tau_{xz} \left( {0,z} \right) \frac{h}{{q_{0} a}} $$
Table 3 Displacements and stresses for an FG plate
Full size table

5 Conclusions

Analytical solution for the free vibration frequencies of FG plates based on 2D elasticity theory is obtained by power series method considering the plane strain condition of the plate. Frequencies of exponentially graded plate are computed for various gradations of the plate and these frequencies should serve as benchmark results. For the sake of completeness, static deflections and stresses in the plate are also calculated although they are already available in earlier reported studies.