Keywords

1 Introduction

As a typical mechatronic system, magnetic levitation technology can achieve high-speed and low-loss movement [1], and high-performance control is of great significance to its research. In the literature about magnetic levitation technology, the magnetic levitation ball system has the one degree of freedom characteristics, so it serves for a simplified model of complicated MLS. Its structure is simple and is easily implemented, so its research contributes to the study of multi-degree-of-freedom MLS [2, 3].

PID control is widely used in the industrial fields, but its parameters are determined by many factors equilibrium position and the controlled objected. The parameters cannot be easily adjusted after the determination. Therefore, when the controlled object changes, the system may change greatly, or even be unstable [4]. Literature [5] finds the suitable values of PID controller parameters by pole placement technique. But the parameters of the controllers needs are changed depending on equilibrium position. Literature [6] used iterative linear matrix inequality technique to derive mathematical modeling and designed a linear feedback PID controller. The method can precisely adjust the position of steel ball by linearization of feedback control system, but the complicated mathematical model is difficultly popularized in industrial promotion. FPID control is a kind of intelligent control and can realize the effective control of complex systems. The fuzzy controller can make the nonlinear system more robust than the PID controller [7, 8]. This intelligent controller can make the MLS stable and is better than the PID controller under parameters change and exogenous disturbance. But the error of the time delay cannot be ignored.

Predictive control can realize setpoint stability control for nonlinear and its robustness and dynamic perform are worth researching [9]. Literature [10] applied the constrained GPC controller to regulate the temperature of an electric vehicle battery. The online self-tuning predictive model adopts CARIMA model whose parameter is calculated by the RLS algorithm. Because the prospective performance cannot be obtained by a single predictive control algorithm, literature [11] combines the sliding mode and the predictive control to control the MLS. But its computational time may be longer than the sampling time, which leads to the instability of the system.

Fuzzy control has strong adaptability and robustness, but its performance relies on the instantaneous response of the system. Therefore, literature [12,13,14] combined PID control, fuzzy algorithm, and predictive control and moreover designed the predictive fuzzy control algorithm. The combination of these three control algorithms can able to good match the input curve and is attractive research. Literature [15] proposed a new PFPID control method. This controller can track dynamic set-point and reject disturbance better, but has the small chatter of output wave in the initial process. Literature [16] designed a model predictive fuzzy PID control algorithm with weights (WM-F-PID) applying into automatic train operation. The input curve is composed of two parts of ideal speed information and future according to a specific weight. The weight is online turned with a steepest descent optimization algorithm. This control algorithm has good robustness and performance in the term of train operation. However, model predictive control (MPC) needs high precision mathematical models and the computational process is cumbersome. Literature [17] proposed a fuzzy generalized predictive controller and the CARMA model is transformed by the T-S fuzzy model of the nonlinear systems. For fuzzy and generalized predictive control, there are obvious advantages and disadvantages. But the mathematical model of this controller is complex and difficult to adjust.

To improve the performance of controller, the controller parameters often are turned to obtain the optimal value with some optimization. Literature [18] proposed the genetic algorithm for optimizing the prediction and control time domain length. However, the controller cannot deal with the change of system parameters well. Literature [19] proposes an automatic tuning method for predictive control using PSO. The optimization method adjusts the weight parameters of controllers according to the predictive control input and particle swarm state. The error of the controller optimized by the PSO algorithm is less than the other optimization algorithm. But the computational time is long and should be set within a reasonable range.

In summary, the MLS has unstable and nonlinear characteristics. Its parameters are easily changed by environmental factors. Based on the existing researches, to remain the system sable in the case of mistake and achieve good static and dynamics performance, a novel magnetic levitation ball location control architecture was proposed in this paper. It is composed of three main parts. The GPC algorithm is the outer control, the FPID control is the inner control, and the PSO algorithm is the optimization algorithm. The input of FPID control algorithm is the future optimal control law predictive by GPC algorithm. The last layer is the PSO algorithm to optimize the parameters of PFPID. According to the above description, the essential part of this controller is generalized as follows:

1) To adapt to the change of maglev system parameters and simplify the complex mathematical process, a PFPID control algorithm was proposed. The control algorithm contains two layers. The GPC on the basis of the CARIMA model serves for the outer layer controller to gain the future optimal control law information. The number of CARIMA model parameters is not large and online turning by RLS algorithm. This control algorithm adopts multi-step prediction and dynamic optimization strategy. It can enhance the adaptive capacity for model mismatch. Then the FPID control is used as the inner layer control algorithm to weaken the influence of parameter changes.

2) Considering the static and dynamic performance, a performance index was proposed based on ITSE objective function, and the PSO algorithm offline optimizes the softening coefficient α and forgetting factor μ of PFPID.

The rest of this article is organized as the following parts. Section 2 analyzes the circuit equations and dynamic equations for the magnetic levitation ball at the equilibrium point, and the mathematical model of controlled object is established. In Sect. 3, presenting a PFPID controller design for magnetic levitation ball position control and an offline PSO algorithm for controller softening coefficient and forgetting factor. In Sect. 4, compared with the PID, PPID, simple PFPID controller, the PSO-PFPID controller has better performance by analyzing data collected in simulation and experiment. In the end, conclusions are summarized in Sect. 5.

2 Analysis and Modeling of MLS

The system device structure is displayed in Fig. 1. This system converts the change of the distance x between the steel ball center and the electromagnet pole monitored by the photoelectric sensor into an electrical signal. After the electrical signal is transmitted to computer, the digital control signal output by computer is converted into an analog signal by D/A converters. Then the analog signal can adjust the instantaneous current i in the electromagnetic coil so that the ball can suspend in the desired equilibrium position by balancing the electromagnetic force F and the steel ball gravity mg.

The MLS is a complex system and its many parameters are uncertain affected by many environmental factors, and there is a complex analysis process for MLS. The experimental environment in this article is relatively stable. So, this paper assumes that some interference for the controller is ignored, such as wind force, the force generated by the sudden change of the power grid, etc. The ball moves only in the vertical direction, so the controlled object has one degree of freedom.

Fig. 1.
figure 1

MLS schematic diagram.

Full size image

(1) The electromagnetic force exerted on the ball in vertical direction is:

$$ F(i,x) = K\left( \frac{i}{x} \right)^{2} $$
(1)

Where k is the force coefficient of the electromagnet.

Because the instantaneous current i in the electromagnetic coil and air gap distance x are nonlinear variables and the process of solving this system is expected to use simple linear theory. The electromagnetic force F is linearized by Taylor expansion at the equilibrium point (i0,x0). The linear electromagnetic force equation is obtained as:

$$ F(i,x) = K_{i} + K_{x} + F\left( {i_{0} ,x_{0} } \right) $$
(2)

where

$$ \left\{ {\begin{array}{*{20}l} {K_{i} = F_{i} \left( {i_{0} ,x_{0} } \right) = \frac{{2Ki_{0} }}{{x_{0}^{2} }}} \hfill \\ {K_{x} = F_{x} \left( {i_{0} ,x_{0} } \right) = - \frac{{2Ki_{0}^{2} }}{{x_{0}^{3} }}} \hfill \\ \end{array} } \right. $$
(3)

Ki is the stiffness coefficient between the electromagnetic force and the coil current, and Kx is the stiffness coefficient between the electromagnetic force and the air gap distance around the balance point.

(2) The dynamic equation of the system

$$ m\frac{{d^{2} x(t)}}{{dt^{2} }} = F(i,x) + mg $$
(4)

The (2) is substituted into (4), the expression is as follow:

$$ m\frac{{d^{2} x}}{{dt^{2} }} = K_{i} \left( {i - i_{0} } \right) + K_{x} \left( {x - x_{0} } \right) $$
(5)

(3) Circuit equation

In order to simplify the derivation process, the electromagnet coil is modeled as consisting of inductance and resistance, and the expression is:

$$ U(t) = Ri(t) + L\frac{di}{{dt}} $$
(6)

Where, R and is L are the resistance and the static inductance of the electromagnetic coil, respectively; U(t) is the voltage applied on the electromagnetic coil.

(4) Boundary conditions

When the steel ball is in an equilibrium position, based on Newton’s second law, the first type of expression of boundary condition can be given as:

$$ mg + F\left( {i_{0} ,x_{0} } \right) = 0 $$
(7)

(5) System model

The output voltage of the drive circuit, the control voltage Uin(s), is defined as the input of the controlled object and is proportional to i(s). The output of controlled object position is expressed by the photoelectric sensor output measured voltage Uout(s), which is proportional to x. The model of the controlled object can be expressed as:

$$ G(s) = \frac{{U_{{{\text{out}}}} (s)}}{{U_{in} (s)}} = \frac{{K_{s} x(s)}}{{K_{a} i(s)}} = \frac{{ - \left( {K_{{\text{s}}} /K_{{\text{a}}} } \right)}}{{\left( {i_{0} /2g} \right)s^{2} - i_{0} /x_{0} }} $$
(8)

In the expression, Ks is the sensor output voltage gain between the air gap distance and the photoelectric sensor output measured voltage, and Ka is the power amplifier gain between the output control voltage of the external circuit and the instantaneous current in the electromagnetic coil.

3 Design of PSO-PFPID Controller

Fig. 2.
figure 2

The structure of PSO-PFPID controller.

Full size image

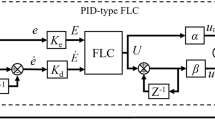
The magnetic levitation ball system has one degree of freedom and is an unstable system with time delay and variable parameters. The design of the controller for this system needs to pay attention to the following two points: Firstly, the effective control methods make original unstable system stable. Secondly, the controller has strong robustness when the controlled object parameters change. This article adopts PFPID controller and optimizes the controller parameters with the particle swarm algorithm. This method can well make the MLS stable. The controller, combined by the predictive control and fuzzy control, can overcome each other's shortcomings and improve the system performance. The structure of PSO-PFPID controller system is expressed in Fig. 2.

3.1 Generalized Predictive Control System Design

The CARIMA model serves for the predictive model of GPC algorithm. Based on the input and output differential equations, the expression of CARIMA model is established at the equilibrium point by linearization and discretization. The mathematical expression is expressed as follow:

$$ \overrightarrow {A} (z^{ - 1} )y(k) = \overrightarrow {B} (z^{ - 1} )u(k - 1) + \frac{1}{\Delta }\overrightarrow {C} (z^{ - 1} )\xi (k) $$
(9)

where,

$$ \left\{ {\begin{aligned} \overrightarrow {A} (z^{ - 1} ) & = a_{{n_{a} }} z^{{ - n_{a} }} + a_{{n_{a} - 1}} z^{{ - (n_{a} - 1)}} + \cdots + a_{1} z^{ - 1} + 1 \\ \overrightarrow {B} (z^{ - 1} ) & = b_{{n_{b} }} z^{{ - n_{b} }} + a_{{n_{b} - 1}} z^{{ - (n_{b} - 1)}} + \cdots + b_{1} z^{ - 1} + 1 \\ \overrightarrow {C} (z^{ - 1} ) & = c_{{n_{c} }} z^{{ - n_{c} }} + c_{{n_{c} - 1}} z^{{ - (n_{c} - 1)}} + \cdots + c_{1} z^{ - 1} + 1 \\ \Delta & = - z^{ - 1} + 1 \\ \end{aligned} } \right. $$
(10)

y(k) and u(k) are the system input and output, respectively; Δ is a differential operator; ξ(k) is a white noise sequence with the average of zero. When the system has a q-beat time delay, there is b0 ~ bq-1 = 0, (q ≤ nb). Considering the model accuracy, na and nb are taken as 9 and 10, respectively. In order to simplify the calculation process, the article assumes C(z−1) = 1.

The identification process of predictive model is the solution of the above polynomials \(\overrightarrow {A} (z^{ - 1} )\) and \(\overrightarrow {B} (z^{ - 1} )\). Then (9) can be rewritten as:

$$ \left\{ {\begin{aligned} \Delta y(k) & = - \widetilde{A}(z^{ - 1} )\Delta y(k) + \overrightarrow {B} (z^{ - 1} )\Delta u(k - 1) + \xi (k) \\ & = \varphi (k)^{T} \theta + \xi (k) \\ \end{aligned} } \right. $$
(11)

where,

$$ \left\{ {\begin{array}{*{20}l} {\overrightarrow {H} (k) = \left[ {\Delta u(k - 1), \cdots ,\Delta u\left( {k - n_{b} - 1} \right),} \right.} \hfill \\ {\left. { \, - \Delta y(k - 1), \cdots , - \Delta y\left( {k - n_{a} } \right)} \right]^{T} } \hfill \\ {\theta = \left[ {a_{1} ,a_{2} , \cdots ,a_{{n_{n} }} ,b_{0} ,b_{1} , \cdots ,b_{{n_{b} }} } \right]^{T} } \hfill \\ {\widetilde{A}(z^{ - 1} ) = \overrightarrow {A} (z^{ - 1} ) - 1} \hfill \\ \end{array} } \right. $$
(12)

The parameter vector θ is identified with the RLS method of fading memory. The recursive formula is expressed as the following formula:

$$ \left\{ {\begin{array}{*{20}l} {K(k) = \frac{Q(k - 1)\varphi (k)}{{\varphi (k)^{T} Q(k - 1)\varphi (k) + \mu }}} \hfill \\ {Q(k) = \mu^{ - 1} \left[ {I - K(k)\varphi (k)^{T} } \right]Q(k - 1)} \hfill \\ {\varepsilon (k) = y(k) - \varphi (k)^{T} \hat{\theta }(k - 1)} \hfill \\ {\hat{\theta }(k) = \hat{\theta }(k - 1) + K(k)\varepsilon (k)} \hfill \\ \end{array} } \right. $$
(13)

In the expression, μ represents the forgetting factor and is generally 0.95 to 1; K(k) is the gain factor vector; Q(k) is the positive definite matrix; \(\hat{\theta }(k)\) is the model parameter error matrix; ɛ(k) is the prediction error.

According to the identified system CARIMA model parameters, the Diophantine equation is introduced to derive the variation of the optimal control law and predictive output value at the future time. The Diophantine expression is as follows:

$$ 1 = z^{ - j} \overrightarrow {F} (j) + \overrightarrow {E} (j)\overrightarrow {A} (z^{ - 1} )\Delta $$
(14)

Where, polynomials \(\overrightarrow {E} (j)\) and \(\overrightarrow {F} (j)\) are derived by \(\overrightarrow {A} (z^{ - 1} )\) and the predictive length j, and are as follows:

$$ \left\{ {\begin{array}{*{20}l} {\overrightarrow {E} (j) = e_{j,j - 1} z^{ - (j - 1)} + e_{j,j - 2} z^{ - (j - 2)} + \cdots + e_{j,0} } \hfill \\ {\overrightarrow {F} (j) = f_{{j,n_{a} }} z^{{ - n_{a} }} + f_{{j,n_{a} - 1}} z^{{ - (n_{a} - 1)}} + \cdots + f_{j,0} } \hfill \\ \end{array} } \right. $$
(15)

On the basis of the system input and output value in the current moment, the predictive system output value at the next j sampling time is obtained as the following:

$$ \begin{gathered} \widetilde{y}(k + j|k) = \overrightarrow {E} (j)\overrightarrow {B} (j)\Delta u(k + j - 1|k) \hfill \\ \, + \overrightarrow {F} (j)y(k) + \overrightarrow {E} (j)\xi (k + j) \hfill \\ \end{gathered} $$
(16)

According to (16), another Diophantine equation is introduced as:

$$ \overrightarrow {G} (j) = \overrightarrow {E} (j)B(j){ = }\overrightarrow {G} (j) + z^{ - 1} \overrightarrow {T} (j) $$
(17)

where,

$$ \left\{ \begin{gathered} \overrightarrow {G} (j) = g_{j,j - 1} z^{ - (j - 1)} + g_{j,j - 2} z^{ - (j - 2)} + \cdots + {\text{g}}_{j,0} \hfill \\ \overrightarrow {T} (j) = t_{{j,n_{b} }} z^{{ - n_{b} }} + t_{{j,n_{b} - 1}} z^{{ - n_{b} - 1}} + \cdots + t_{j,1} z^{ - 1} \hfill \\ \end{gathered} \right. $$
(18)

In order to achieve soft control, the system output does not directly track the set value, but the target value of the control tracks the reference trajectory R(k + j), which is expressed as the following expression:

$$ \begin{gathered} R\left( {k + j} \right) = \alpha^{j} y(k) + \left( {1 - \alpha^{j} } \right)y_{R} \left( {k + j} \right), \hfill \\ \left( {j = N_{1} ,N_{1} + 1, \ldots N_{2} } \right) \hfill \\ \end{gathered} $$
(19)

Where yR(k + j) is the expected output value in the future, that is, the output reference value.

In the GPC controller, the output value is expected to track the ideal input value as much as possible, and then the performance index is defined as:

$$ \begin{gathered} \begin{array}{*{20}c} {\min J(k) = E\left\{ {\mathop \sum \limits_{j = 1}^{{N_{\mu } }} \lambda (j)[\Delta u(k + j - 1)]^{2} } \right.} \\ {\left. {\quad \quad \; + \mathop \sum \limits_{{j = N_{1} }}^{{N_{2} }} [y(k + j\left| k \right.) - R(k + j)]^{2} } \right\}} \\ \end{array} \hfill \\ \, \hfill \\ \end{gathered} $$
(20)

Where E{·} is the mathematical expectation; N1 is the starting time of the predictive time domain; N2 is the ending time of the predictive time domain; Nμ is the control time domain length, and the control law does not change after Nμ sampling time; λ(j) is the control weighting factor, the control weighting factor is taken as 1.

In order to make the calculation process easier to understand, the paper uses a matrix to describe the relatively lengthy calculation process. According to (16) and (20), taking the partial derivative of J(k) as 0 can obtain the following control law with the local optimal performance index expression as:

$$ \Delta {\varvec{U}}\left( {{\rm k}\left| {\rm k} \right.} \right) = \left( {{\varvec{G}}^{T} {\varvec{G}} + \lambda {\varvec{I}}} \right)^{ - 1} {\varvec{G}}^{T} \left[ {\overrightarrow {R} (k) - {\varvec{C}}({\rm k})} \right] $$
(21)

where,

(22)

GPC control decision is based on predictive future system information, and the selection of predictive information affects the selection and design of the inner controller. To overcome the influence of the time lag on the system, the input of the inner controller adopts the value of the optimal control law in the future time. The variation of the optimal control law of Nμ-1 steps at time k and the control law at the current time are accumulated to obtain the predicted optimal control law of inner controller. The predicted optimal control law expression is as follows:

$$ u(k) = u(k - 1) + [0 \, 0 \cdots 0 \, 1]*\Delta {\varvec{U}}(k|k) $$
(23)

The online control steps of GPC are described as follows:

  1. 1)

    Initialization: Set the CARIMA model identification parameter range number na and nb, the prediction domain starting and ending time N1 and N2, the control time domain length Nμ, and the RLS algorithm initial value θ(−1) = 0, P(−1) = α2I.

  2. 2)

    On the basis of the latest system input and output information, calculate the system predictive model parameters \(\overrightarrow {A} (z^{ - 1} )\), \(\overrightarrow {B} (z^{ - 1} )\) by (13).

  3. 3)

    According to the obtained \(\overrightarrow {A} (z^{ - 1} )\), \(\overrightarrow {B} (z^{ - 1} )\) and the Diophantine equation, recursively calculate \(\overrightarrow {E} (j)\), \(\overrightarrow {F} (j)\), \(\overrightarrow {G} (j)\), \(\overrightarrow {T} (j)\).

  4. 4)

    Calculate the optimal control law change rate ΔU(k|k) by (21).

  5. 5)

    Calculate the predicted optimal control law u(k) by (23), and substitute u(k) into the control system.

  6. 6)

    Obtain system input and output information at the current time, take k = k + 1, and back to step 2).

3.2 Fuzzy PID Control Design

In this article, the FPID controller is established on the two-dimensional fuzzy logic. There are two inputs and three outputs composing the FPID controller. The error e and the error change rate ec serve for the controller input variables. The controller output variables select the PID parameters change rate ΔKp, ΔKi, and ΔKd. The controller gets input variables, then continuously turns the parameters of the PID controller to meet the control requirements in different situations. The adjustment expression of PID parameters are as follows:

$$ \left\{ {\begin{array}{*{20}l} {K_{p} = K_{p0} + \Delta K_{p} } \hfill \\ {K_{i} = \, K_{i0} + \Delta K_{i} } \hfill \\ {K_{d} = K_{d0} + \Delta K_{d} } \hfill \\ \end{array} } \right. $$
(24)

Where KP0, Ki0, Kd0 are the initial setting values of KP, Ki, Kd, which are obtained by the normal PID tuning method.

In FPID controller, the basic domains of the error e and the error change rate ec respectively are [−0.6, 0.6], [−0.3, 0.3]. The basic domains of output ΔKp, ΔKi, ΔKd respectively are defined as [−2, 2], [−2, 2], [−0.02, 0.02]. The basic domain of input and output is the same as the fuzzy domain, that is, the quantization factor is 1. According to the control experience and requirement, the input and output are fuzzified to fuzzy subsets including seven levels. These levels are negative big, negative medium, negative small, zero, positive small, positive medium, and positive big in fuzzy subsets, simplified as [NB, NM, NS, Z, PS, PM, PB]. A triangular membership function serves for the membership function in this paper. Because its shape can be changed by only selecting the straight-line slope and it is suitable for online adjustment. In addition, Mamdani reasoning is adopted as the fuzzy reasoning method and the defuzzification method chooses the center of gravity method. The control rules of the fuzzy controller are obtained based on the basic rules of fuzzy rules, PID parameter self-adjustment rule and the generalized control experience of MLS control experts. The rules between the input variables and output variables are shown in Table 1.

Table 1. The fuzzy rules table of ΔKp/ΔKi/ΔKd.
Full size table

3.3 Particle Swarm Optimization Algorithm

Suppose the particle is modified in an M-dimensional space and there are N particles constituting a particle swarm. A M-dimensional vector Xi = (xi1,xi2,xi3, …,xiM) can represent the position of the particle in the space; a M-dimensional vector Vi = (vi1,vi2, vi3,…,viM) can also express the velocity of the particle; the optimal position of individual and global particle at the current instance can be recorded as Pi = (pi1,pi2, …,piM) and Gbest=(g1,g2…,gM), respectively. Based on the optimal value, the coordinates of particles position and velocity are modified as the following expression:

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{V}}_{i} (k + 1) = w \cdot {\varvec{V}}_{i} (k) + c_{1} \cdot r_{1} \cdot \left( {{\varvec{P}}_{i} (k) - {\varvec{X}}_{i} (k)} \right)} \hfill \\ {\quad \quad \quad \quad \quad \quad + c_{2} \cdot r_{2} \left( {{\varvec{G}}_{best} - {\varvec{X}}_{i} (k)} \right)} \hfill \\ {{\varvec{X}}_{i} (k + 1) = {\varvec{X}}_{i} (k) + {\varvec{V}}_{i} (k + 1)} \hfill \\ \end{array} } \right. $$
(25)

In the formula, c1 and c2 represent learning factors; r1 and r2 are random numbers, which are generally from 0 to 1; k is the number of iterations; w is the inertia factor.

Based on tracking trajectory information, the optimal control law is obtained with GPC algorithm, so the softening coefficient α of PFPID has an important influence on the tracking trajectory. According to (19), provided that α is reduced, w(k) would quickly approximate yr so that the celerity of tracking is increased and the robustness is reduced and vice versa. Therefore, the value α must be considered between dynamic quality and the robustness. It is generally 0 to 1. The forgetting factor μ is important for the CARIMA model parameters identification. If μ is small, the system has good tracking ability, but at the same time the influence of noise is increased and vice versa. A suitable forgetting factor μ can balance the estimation error and the tracking ability of the controller. It is generally 0.95 to 1.

To weaken the system output chatter and reduce the overshoot of the step response, the change rate of system error ec is taken as the optimization target. At the same time, aiming to reduce the influence of the initial trial error and to weigh the error fluctuations that appear in the later stage of the response, the time t is taken as optimization goals. This paper combines ITSE indicator and then proposed a fitness function. The combination coefficient is determined based on researcher’s experience. The corresponding fitness function is as follows:

$$ J_{2} = \int {t \times \left( {1.5\left| {e_{c} (t)} \right|^{2} + 0.1\left| {e(t)} \right|} \right)dt} $$
(26)

The optimization algorithm can be expressed via the following steps in Fig. 3.

Fig. 3.
figure 3

Flow chart of offline particle swarm optimization.

Full size image

4 Simulation and Experiment Analysis

To validate the availability of the PSO-PFPID controller in practice, the Googoltech GML2001 magnetic levitation ball experimental device is used as the experimental device, and it is a typical suction suspension maglev system and a simplified platform for magnetic levitation technology. The physical model parameters of the controlled object are shown in Table 2 by measurement.

Table 2. Actual system parameters
Full size table

After the physical parameters are plugged into (8), the transfer function expression of the magnetic levitation ball system can be expressed as:

$$ G(s) = \frac{1043.19}{{s^{2} - 623.956}} $$
(27)

4.1 Simulation Analysis

To validate the availability and dynamic characteristics of the PSO-PFPID controller, MATLAB/Simulink is selected as the platform conducting simulation based on the above transfer function. Firstly, some parameters of the PFPID controller are set. The reasonable number of the prediction time domain is generally to have 10 to 25 sampling steps obtaining the transient system information. In general, the length of control steps is 20%–35% of the pre-diction domain length. For simplifying the large numbers of calculations, the start time step and the end time step of the prediction time domain are 1 and 12 respectively, and the number of control steps is 4. The PID controller is important to stabile the internal loop system. Based on the trial-and-error method, the initial setting values KP0, Ki0, Kd0 are 8.5, 10, 0.495.

In the PSO algorithm, the particle number is 50; the iteration number is 50; the learning factors c1 and c2 are 0.6 and 0.7, respectively; the particle dimension is 2. The particle swarm optimization process is shown in Fig. 4 as follows.

Fig. 4.
figure 4

Particle swarm change curve.

Full size image

The paper analyses that the performance indexes of PSO-PFPID controller and compares the controller with the PID, PPID, and simple PFPID, when these algorithms track a reference waveform (RW). The output waves comparison of the above controllers are displayed in Fig. 5.

Fig. 5.
figure 5

Comparison of position-tracking wave based on different controllers.

Full size image

As Fig. 5 shows, the PID controller has larger over-shoot and longer transient time. When the inner controller of the GPC adopts PID, the system has shorter transient time and no overshoot. The transient time of the PPID system is 1.2575 s, 2.1541 s, 2.340 s, 2.2173 s, respectively at sampling point 1, 2, 3 and 4. Although the GPC and fuzzy algorithm improve the dynamic performance and reduce overshoot, the performance indicator is relatively poor influenced by the controller parameters and the response has fluctuation in each initial time, so the parameters of PFPID need to be optimized globally. After the optimized softening coefficient α and forgetting factor μ are substituted into PFPID controller, the system by PSO-PFPID control algorithm improves the performance of rapidity and stability. The transient time of the PPID system is 1.4274 s, 1.581 s, 1.6166 s, 1.7636 s, respectively at sampling point 1, 2, 3 and 4. The control algorithm proposed in this article has excellent comprehensive control performance, especially in the matter of dynamic response.

To compare the tracking performance of the PSO-PFPID controller for different system parameters, the transfer function of the controlled object is adjusted appropriately. The robustness of the algorithm is tested in the cases of model mismatch. The original and adjusted transfer functions of the controlled object are as follows:

$$ \left\{ {\begin{array}{*{20}l} {G(s) = \frac{850}{{s^{2} - 600}}(case1)} \hfill \\ {G(s) = \frac{950}{{s^{2} - 500}}(case2)} \hfill \\ {G(s) = \frac{1150}{{s^{2} - 750}}(case3)} \hfill \\ {G(s) = \frac{1043.19}{{s^{2} - 623.956}}(origin)} \hfill \\ \end{array} } \right. $$
(28)

When the model parameters change, the tracking trajectory of the original system and the adjusted system is shown in Fig. 6.

Fig. 6.
figure 6

Comparison of position-tracking wave based on different model parameters.

Full size image

As Fig. 6 shows, when the parameters of the controlled object are adjusted appropriately, PSO-PFPID controller still can make different controlled objects stable and track input square signal well. These control systems have no overshoot and well dynamic and steady state performance. Therefore, the PSO-PFPID controller is a feasible and effective position-tracking controller and has strong robustness for the model mismatch.

4.2 Experiment

Based on MATLAB/Real-Time Windows Target, the experiment of the magnetic levitation ball system is conducted and the system ability to track the signal is analyzed in the case of mismatch. Therefore, the following experimental process is designed: According to the relationship between the input voltage and the position, the distance between the steel ball and the bottom of the electromagnet is set to 1 cm by controlling the input signal. Then adding a step signal in 30 s makes the position of the magnetic levitation ball increase by 0.2 cm. To validate the trace ability of the PSO-PFPID controller for different objects, the clips are added on the steel ball. To adjusting the parameters of the controlled object, the numbers of clips are 4(case4), 6(case5) and 8(case6). One clip weighs 0.02 kg. In different situations, the position changes of the steel ball are shown in Fig. 7.

Fig. 7.
figure 7

Comparison of experimental results based on the different objects.

Full size image

From Fig. 7, the PSO-PFPID control algorithm not only makes the ball stably suspend, but also has good robustness. When the system model is mismatched, the controller still maintains better tracking performance. The PSO-PFPID control algorithm not only has the advantage of no overshoot, but also can well cope with the changes of system parameters.

5 Conclusion

Focusing on minimize the influence of the time lag and the uncertain parameters of the mathematical model, this paper proposed a cascaded PSO-PFPID controller and verified the feasibility of the algorithm. More specifically, the outer controller adopts GPC to minimize the error resulted from the time lag. The CARIMA model is used as the prediction model and its parameters are online identified by RLS algorithm, on the basis of the system input and output value at the present and past moments. The optimal control law in the next Nμ-1 sampling time is predicted by GPC algorithm. The inner controller adopts a FPID controller. It can effectively deal with different parameter changes. Finally, to design the controller having the better static and dynamic performance, the softening coefficient α and forgetting factor μ of the predictive controller are globally optimized by PSO. The magnetic levitation ball system is chosen as the simulation and experiment object. The results imply that, compared with conventional control method PID, PPID and simple PFPID, the PSO-PFPID controller can relatively reduce response time and maintain good tracking performance even in the case of model mismatch. The controller has strong robustness. However, the offline optimization method was adopted, so the total operating time is long. In future work, the complex calculation will be improved to suit complex MLS. Future research in this field is worthwhile.