Double Generating Functions Approach to Quadrupedal Trot Gait Locomotion

Abstract

This paper introduces a double generating functions based method for the trot gait locomotion of the quadruped robot. A virtual leg technique is employed to simplify the quadrupedal model to a bipedal model, the double generating functions based algorithm is given to generate the energy optimal trot gaits, and finally a comparison between the introduced method and CPG based method illustrates the substantial advantage of the method. The double generating functions method belongs to the model based locomotion method, but due to its particular algorithm structure it is efficient in online computation. furthermore, it can give more detailed planning such as optimal energy consumption and gait pattern control than that of the popular bionic based methods. Though the simulation is for the linear dynamics, the introduced method also works well for the nonlinear system by involving the PD tracking control technique.

This work is supported by the National Natural Science Foundation of China (Grant No. 62003321), and Natural Science Foundation of Zhejiang Province, China (Grant No. LQ19F030006 and LQ20E050017).

1 Introduction

Among legged robot, the quadruped robot possesses a moderate number of feet, good motion performance and high carrying capacity, hence has a broad application prospect [1]. The quadrupedal gait locomotion has been one of the focus research in the robot field for years. At present, model based and bionic based methods are the two common control strategies applied to quadruped robot gait locomotion [2]. Model based method is a traditional quadrupedal locomotion method, its control idea is modeling-planning-control [3]. M. Raibert proposes the application of a virtual leg model to control the gait of a quadruped robot [4], and his team develops the first jumping robot in the world with a spring-loaded inverted pendulum model as a robot dynamics model [5]. D. Gong builds a relative complete three-dimensional model of a quadruped robot, and the inverse kinematics of the model is used to plan the leg trajectory [6]. A. W. Winkler uses a simplified centroidal dynamics model to represent the leg movement of a quadruped robot, which is affected by the position and force of the foot [7]. X. Chen employs the spiral theory to analyze the mobility of quadruped robot [8]. In the process of establishment of the kinematic model, the robot body is divided into translation and rotation of the body center. The bionic based method via CPG (central pattern generator) is that researchers conduct engineering simulation, simplification and improvement on the CPG, neural vibrator, biological reflection and so on, gradually form a more scientific motion control method and theory, which can be used to realize the control of robot rhythmic motion [9]. Among the existing CPG models, the Matsuoka differential oscillator model proposed by Matsuoka has simple mathematical expression and clear biological significance, and is widely used in rhythmic motion control of robots. Then H. Kimura introduces feedback signal based on this model, and simulates the influence of external interference on the stability of the system [10]. Y. Fukuoka verifies the effectiveness and accuracy of Kimura’s improved CPG model through the gait control experiment of tekken quadruped robot [11]. H. Zheng modifies and refines Mastuoka’s oscillator model, and verifies the effectiveness of robot rhythmic motion control method based on biological CPG control mechanism through simulation [12]. A nonlinear oscillator is introduced as the mathematical model of CPG, which can generate the rhythmic signal output when CPG lacks sensor feedback [13]. Based on the nonlinear oscillator model, Hopf model and Van der Pol model are widely used in practical engineering [14]. Compared with Kimura CPG model, the parameters of Hopf oscillator correspond to amplitude, phase and frequency one by one. It has the characteristic of limit cycle and is suitable for the gait planning of the legged robot.

In the field of robot, the energy consumption in the process of robot walking is an important problem to be studied. This problem can be formalized as a standard optimal control problem, which can be solved by Riccati transformation method [15], shooting method, parameter optimization and other methods [16, 17]. However, when dealing with a large number of different boundary conditions, these methods ignore the importance of online computing, which makes the efficiency of online gait generation very low. In recent years, the problem of optimal trajectory generation considering energy consumption has been widely studied in the field of robotics. Recently, C. Park proposes a single generating function (GF) method based on optimal trajectory generation, which can generate their optimal trajectory under different boundary conditions [18]. Z. Hao applies the method of double GFs to the gait planning of bipedal walking robot when walking on flat ground. By using this method, the finite time linear quadratic (LQ) optimal control problem is solved and the optimal gait and input torque are generated under the condition of considering the optimal energy [19]. In this method, the numerical integration required in the traditional GF method is implemented offline, and only simple algebraic operation is carried out online, which reduces the effort of online calculation of the system. In this paper, the GF based method is extended to the trot gait locomotion of the quadruped robot. The virtual leg technology is used to build the dynamic model of the diagonal gait of quadruped robot. By simplifying the model, the complex and tedious derivation can be reduced. The problem of energy optimal robot locomotion problem is transformed to the optimal control problem by using the energy related performance index. At the same time, a pair of suitable GFs are introduced into the regular transformation of Hamiltonian system to solve the optimal control problem, and the optimal trajectory generated by GF is derived. Finally, the real time performance and energy consumption index of the algorithm are studied by comparing the two different types of robot locomotion methods.

2 Dynamic Model

2.1 Virtual Leg Technique

Fig. 1.

Diagram of Virtual leg technique and virtual leg (the red dotted line) of quadruped robot in trot gait (Color figure online)

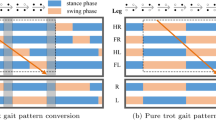
As shown in Fig. 1(a), virtual leg technique is a structural simplification of the gait of the quadruped robot with the legs moving in pairs [20]. Compared with the original model, virtual legs have exactly the same function. With the help of the technique, the quadrupedal trot gait can be treated as the bipedal gait. In detail, the robot diagonal legs in each motion cycle have the same phase, which meets the required condition of the technique that the diagonal legs in trot gait can be replaced by the virtual legs at the center of mass of the robot body. Thus, the quadruped robot can be regarded as a biped robot, and its model can be treated as a bipedal model, which is shown in Fig. 1(b).

2.2 Dynamic Model of Robot

In the process of modeling, the size and shape of the robot body are ignored, but its mass is preserved, and the robot is simplified as a particle with mass. Each leg of the robot is equivalent to a link connecting the common body, each leg has two rotational degrees of freedom of hip joint and knee joint. In addition, the counterclockwise direction is the positive direction selected in this paper. As shown in Fig. 2, the physical parameters and variables in the modeling process are: m_H is the mass of the body of the robot, m₁ the mass of the leg, m₂ the mass of the thigh, a₁ the distance from the center of gravity of the leg to the foot end, b₁ the distance from center of gravity of the leg to the knee joint, b₂ the distance from the center of gravity of the thigh to the hip joint, L₁ the length of the leg, L₂ the length of the thigh, g the acceleration of gravity, θ₁ and θ₄ are the angles of equivalent knee joints, θ₂ and θ₃ are the angles of equivalent hip joints, u₁ and u₄ are the input torques of knee joints, u₂ and u₃ are the input torques of hip joints. Moreover, it is assumed that the transition of the supporting leg occurs instantaneously when the swinging leg touches the ground and previous supporting leg leaves the ground, the collision of the swinging leg with the ground is assumed to be inelastic and without sliding, and there is no sliding between the support leg and the ground.

Fig. 2.

Model of biped walking robot

The virtual leg technique is employed here to establish a simplified dynamic model of the quadruped robot with trot gait. Because the shape of the body is ignored, the motion of the robot is mainly described by the action of the legs. Such a system can be seen as a four-bar linkage system. We use the Euler–Lagrange method to build the dynamic model of the quadruped robot.

$$ M(\theta )\ddot{\theta }\, + \,N(\theta ,\dot{\theta })\dot{\theta }\, + \,G(\theta )\, = \,u. $$

(1)

where $\theta : = \left( {\theta_{1} ,\theta_{2} ,\theta_{3} ,\theta_{4} } \right)^{{\text{T}}}$ is the generalized coordinate vector, the vector of the joint torques is denoted as ${\text{u: = }}\left( {{\text{u}}_{{1}} {\text{,u}}_{{2}} {\text{,u}}_{{3}} {\text{,u}}_{{4}} } \right)^{\rm T}$, ${\text{M}} \in {\text{R}}^{4 \times 4}$ is the generalized mass matrix, ${\text{N}} \in {\text{R}}^{4 \times 4}$ the Coriolis forces matrix, and ${\text{G}} \in {\text{R}}^{4}$ the gravity term and stiffness matrix.

Although the biped robot model reduces the complexity and redundancy of the model, it is still a multivariate and highly nonlinear equation. In order to start the following algorithm research, we linearize it firstly. We define the state variable ${\text{x}}: = \left( {{\uptheta }{}_{1},{\uptheta }_{2} ,{\uptheta }_{3} ,{\uptheta }_{4} ,{\uptheta }_{1}^{ \cdot } ,{\uptheta }_{2}^{ \cdot } ,{\uptheta }_{3}^{ \cdot } ,{\uptheta }_{4}^{ \cdot } } \right)^{\rm T}$, where the variables in the right hand side are denoted by x₁, x₂, x₃, x₄, x₅, x₆, x₇, and x₈ respectively. By combining with

$$ \dot{x}_{1} = x_{5} ,\;\dot{x}_{2} = x_{6} ,\;\dot{x}_{3} = x_{7} ,\;\dot{x}_{4} = x_{8} , $$

we obtain the dynamic equation

$$ \dot{x}\, = \,f(x,u) $$

(2)

where the nonlinear function f: = ${\text{R}}^{8} \times {\text{R}}^{4} \to {\text{R}}^{8}$.

In order to get the zero position of the robot, we use Taylor expansion of the nonlinear function f(x,u). When (x,u) = (0,0), the nonlinear function $\dot{x} = f\left( {x,u} \right) = \left( {0,0} \right)$ representing that the state variable x(t) is constant for all t. At this time, the robot belongs to the static state, the angular velocity and the input torque of each joint are all zero, so (x,u) = (0,0) is called as the balance point of the robot. Finally, the linearized version of the dynamic Eq. (2) is

$$ \dot{x} = Ax + Bu $$

(3)

where the parameters

$$ A = \left. {\frac{{\partial f\left( {x,u} \right)}}{\partial x}} \right|_{{\left( {x,u} \right) = \left( {0,0} \right)}} , $$

$$ B = \left. {\frac{{\partial f\left( {x,u} \right)}}{\partial u}} \right|_{{\left( {x,u} \right) = \left( {0,0} \right)}} $$

3 LQ Optimal Control Problem and Double GFS Based Method

3.1 Energy Optimal Control Problem

For the robot locomotion, the problem of energy consumption has always been a research hotspot. In fact, this problem is to generate the input torque and the walking pattern (joint angle) of the robot during walking. It can be expressed by minimizing the cost function of the angle and the torque during the trajectory generation. Here, we set a cost function with the consideration of the energy

$$ J\left( {u;x\left( {t_{0} } \right)} \right) = \frac{1}{2}\mathop \smallint \limits_{{t_{0} }}^{{t_{f} }} \left( {x^{\rm T} Qx + u^{\rm T} Ru} \right)dt, $$

(4)

where the constant $Q \in {\mathbb{R}}^{8 \times 8}$ is positive definite, $R \in {\mathbb{R}}^{4 \times 4}$ is positive definite, and t₀ and t_f are the initial and terminal times respectively.

Based on the above, then the energy-optimal trot gait locomotion problem of the quadruped robot (biped model equivalently) can be formulated as

Problem 1.

$$ \mathop {min }\limits_{u} J\left( {u;x\left( {t_{0} } \right)} \right), $$

$$ s.t.\,\dot{x} = Ax + Bu , $$

$$ x\left( {t_{0} } \right)\, = \,x_{0} , \, x\left( {t_{f} } \right)\, = \,x_{f} \cdot $$

on the fixed time interval $t \in \left[ {t_{0} ,t_{f} } \right]$. The vectors x₀ and $x_{f} \in {\mathbb{R}}^{8}$ are the given values of the fixed initial and terminal configuration states, respectively.

The optimal trajectories of the joint angles and input torques are obtained by minimizing the cost function (4). The state equation in Problem 1 is the linearized version of the robot dynamics derived in the previous section. In the fixed time interval [t₀, t_f], the time values x₀ and x_f representing the initial and terminal values of the body posture of a robot in a gait cycle respectively, are the boundary conditions for solving the energy-optimal trot gait locomotion problem of the quadruped robot (Problem 1).

3.2 GF Method and Optimal Trajectory Generation

Problem 1 is solved via double GFs based method. A pair of GFs is introduced and their expressions are exhibited. Finally, the optimal state and input trajectories are given by such a method. The detailed algorithms are as follows.

Algorithms 1 and 2 represent the online part and offline part of the GF algorithm respectively. In the case of complex model, it takes a lot of efforts to solve ordinary differential matrix equations, while this part is solved offline by double GFs method according to Algorithm 1, which greatly improves the efficiency of the computation. In Algorithm 2, the boundary conditions x₀ and x_f, the initial time t₀, and the terminal time t_f can be easily changed to generate different optimal trajectories according to the task requirements. The reason is that in Algorithm 2, all of them are algebraic operations, when the robot needs to change the boundary condition parameters when switches the gait, the effort of online calculation brought by this change is almost zero.

4 Trot Gait Locomotion via Double Gfs and CPG Based Methods

This section compares the simulation results of the double GFs based algorithm with the CPG based bionic control algorithm. According to the comparison, this section exhibits the particular advantage of the double GFs based method.

The parameters of the quadruped robot in this section are chosen as l₁ = l₂ = 0.16 [m], a₁ = a₂ = 0.08 [m], b₁ = b₂ = 0.08 [m], m₁ = m₂ = 1/6 [kg], m_H = 4/3 [kg], g = 9.8 [m/s²]. Based on some tentative simulations, we select the parameters Q = I_8×8 and R = diag (1, 1, 2, 3).

4.1 Locomotion via Double Gfs Based Method

After the parameters of the robot are selected, the matrices A and B in the linearized dynamic equation can be determined. Now we only need to determine the boundary conditions x₀, x_f, and the gait period T to get the optimal state and the input trajectories.

In our previous equivalent bipedal model of the quadruped robot, we assumed that the time period for the robot to walk one step started at the moment when the swinging leg currently raises, and ends at the next transition moment when the swinging leg falls and the supporting leg alternates. As shown in Fig. 3, the dotted line in the figure is the transition position of the support leg during the robot walking one step.

In fact, due to the limitations of the physical prototype in the design of the mechanism, the rotation angles of the hip and knee joints of the quadruped robot can only be constrained within a specific range. In this paper, the robot hip joint angle range $\theta_{h} \in \left[ {105^\circ ,165^\circ } \right]$ and the knee joint angle range $\theta_{k} \in \left[ { - 60^\circ , - 120^\circ } \right]$. The configuration of the initial joint of a leg of the quadruped robot is exhibited in Fig. 3.

Fig. 3.

Diagram of gait switching and initial configuration.

For convenience, we set the initial configuration of the robot as

$$ x_{0} = \, \left( { - {3}0^{ \circ } ,{ 6}0^{ \circ } ,{ 45}^{ \circ } , \, - {48}.{78}^{ \circ } , \, 0, \, 0, \, 0, \, 0} \right)^{\rm T} $$

According to a gait cycle (T = 1 [s]) of the CPG, the end state can be obtained

$$ x_{f} = \, \left( { - {48}.{78}^{ \circ } ,{ 45}^{ \circ } ,{ 6}0^{ \circ } , \, - {3}0^{ \circ } , \, 0, \, 0, \, 0, \, 0} \right)^{\rm T} $$

Assume that the initial and end configuration of a robot walking step are stationary, that is, the angular velocity of each joint is zero. In order to maintain the principle of control variables, we set the gait cycle of the robot to take a step to be the same as the CPG method to plan a step. That is $T \in \left[ {t_{0} ,t_{f} } \right] = \left[ {0,1} \right]$.

Fig. 4.

PD tracking control system block diagram.

Fig. 5.

Reference angle trajectories via double GFs based method and the tracking ones by the PD tracking control and reference angular velocity trajectories via double GFs based method and the tracking ones by the PD tracking control.

Fig. 6.

The generated joint torque u and the cost function value J (t).

At the same time, we considered the modeling error caused by the linearization of the nonlinear robot model. A PD controller is built to track the trajectory. The system block diagram is shown in Fig. 4.

Figures 5 show the reference optimal angle and angular velocity trajectories obtained by the double GFs based method and also the tracking ones of the nonlinear system by the PD tracking control technique. As can be seen from the two figures, the tracking trajectories of the original nonlinear dynamic system are close to the reference ones generated by the double GFs based algorithm. The errors are small and can be almost ignored. It implies that the introduced double GFs based algorithm does also work for the nonlinear dynamics via PD tracking control, which widens the application of the method.

Figure 6 gives the corresponding input torque trajectories in 1 [s] via double GFs. It can be seen from the figure that the changes of the joint torques are relatively large at both initial and terminal moments, but the absolute value of the remaining joint torque values do not exceed 2 [N m], and the maximum value of the whole process does not exceed 6 [N m], which demonstrates the appropriateness of the introduced method to small gait locomotion in practice.

After the optimal control is obtained, we can calculate the value of the cost function according to (4) in the time range of [t₀, t]. Figure 6 gives the trajectory of the energy related function value in a gait cycle. As can be seen from the figure, the value of the function monotonically increases, and the growth rate after t > 0.6 [s] is faster than the time period of 0 < t < 0.6 [s], which shows that the energy change rate during the robots leg retracting phase is greater than the starting and raising legs the rate at which the energy changes in stages.

4.2 Locomotion via CPG Based Method

We plan a gait cycle using the same initial state of the robot as the previous subsection for the CPG based algorithm. For convenience, we set the key parameters µ₁ = µ₂, ω₁ = ω₂ = 2π. Based on this, we give the trajectories of joint angles in Fig. 7, where we take ten cycles of simulation time. The blue and red curves in the two figures represent the changes in the hip and knee joint angles of the robot left front (LF) and right front (RF) legs. Because the robot is in trot gait, the amplitude and phase of the diagonal legs are exactly the same.

In order to compare with the double GFs based method, we need to calculate the energy consumed by the CPG based method here. We observe from the original dynamic model (1) that the M, N, and G on the left hand side are matrices containing ${\uptheta }$ and its first and second derivatives. You need to substitute the variables ${\uptheta }$, ${\dot{\theta }}$, and ${\ddot{\theta }}$ to get the trajectory of the joint torque u. However, the bionic CPG based method only obtains the joint angle value. We get the value of ${\dot{\theta }}$ and ${\ddot{\theta }}$ in the corresponding time by the difference algorithm, which is listed below.

$$ f_{1} \left( {m\, - \,1} \right)\, = \,f \, \left( {m\, + \,1} \right)\, - \,f \, \left( {m\, - \,1} \right)/2h $$

$$ f_{2} \left( {m\, - \,1} \right)\, = \,f \, \left( {m\, + \,1} \right)\, + \,f \, \left( {m\, - \,1} \right)\, - \,2f \, (m) $$

where f (m) is the ${\uptheta }$ angle curve obtained by CPG planning, m is the number of discrete sampling points, h is the step size, and f₁(m) and f₂(m) are the first and second derivatives of f(m), which is shown in Fig. 7.

Because the CPG method provides the relative angle, we need to add the corresponding initial joint angle x₀ of the robot in the process of calculating the torque. The trajectory of the joint torque can be obtained by substituting into the dynamic equation, which is shown in Fig. 8(a). It shows that the quadruped robot walks exactly one step (one gait cycle). The calculated joint torques of the robot during walking (the diagonal leg torque values remain the same). It also shows that during one step process of the quadruped robot, the hip and knee joint torques of the supporting leg (RF leg) are very small in amplitude, while the torque of the swinging leg (LF leg) is relatively large, and the knee joint amplitude is about 3 [N m], the amplitude of the hip joint is about 4 [N m].

After obtaining the input torque u, we still calculate the value of the cost function in the time range of [t₀, t] according to (4). The current value of the energy cost function J (t) over a gait period T is shown in Fig. 8(b). It can be seen from the figure that when the robot planned by the CPG bionic method walks one step under the same conditions, the cumulative value of the energy related cost function monotonically increases with the increase of the time t, and the total amount is significantly greater than that of the double GFs based method (almost six times).

Fig. 7.

Trajectories of hip and knee joint angles of the LF and RF legs and trajectories of angle, angular velocity, and angular acceleration of each joint.

Fig. 8.

The generated joint torque and cost function trajectories.

5 Conclusions

In this paper, the double GFs method is introduced to the trot gait locomotion of the quadruped robot. This method can put a lot of tedious differential equation calculation process offline, and has the advantages of high efficiency of online planning and the ability to plan for different boundary conditions at the same time. Though the double GFs method belongs to the model based method, such a particular algorithm structure makes the method as efficient as the bionic based method, hence is more efficiency than almost all the other model based locomotion approaches.

In addition, the robot dynamics model needs to be linearized during application, because the method is planned for a linear system, and the modeling errors caused by linearization can be adjusted and controlled by the PD tracking control technique involved. In the simulation, we compare the double GFs based method with the CPG based method in the domain of energy consumption in the planning step by using the equivalent phase synchronization length d = 0.28 [m] and the same gait period T = 1 [s] with the same boundary conditions. The energy consumption obtained from the introduced method is about 17.5% of the CPG based method in this paper.