Introduction

Most of the flows in internal combustion engines are turbulent flows, which is one of the most challenging topics in the whole scientific world. The fundamental challenge is that the turbulent flow involves a wide range of timescale and length scale; i.e. the ratio of maximum scale and minimum scale is huge. To exactly model the turbulent flow (direct numerical simulation, DNS), the smallest timescale and length scale should be resolved in the numerical simulation. According to Kolmogorov’s turbulence law (Kolmogorov 1991), both the smallest length and timescales, which are called the Kolmogorov scales, are proportional to \({\text{Re}}^{ - 3/4}\). For a three-dimensional case, the total grid number is proportional to \({\text{Re}}^{ - 9/4}\). Plus the total time step, the total computational cost is proportional to \({\text{Re}}^{3}\). The Reynolds number in engines is usually very large. Plus, the chemical reactions and multiphase flow make the situation even much complex. All of these factors prevent the DNS from engine simulations. A description of the system at a coarser level is required to make engineering simulations possible. The Reynolds-averaged numerical simulation (RANS) method (Chaps. 16 and 17) is a feasible way for engine simulations with affordable computational costs. The RANS model employs a time-averaging technique to simplify the problem so that the larger time step and grid size can be used. A lot of physics, especially unsteady behaviours, have been ignored.

An alternative is the large eddy simulation (LES), which adopts a volume averaging technique to avoid resolving the smallest scales. As it is named, LES explicitly computes the large eddies of the flows, usually whose sizes are larger than the grid size. The effects of the smaller ones are modelled using a sub-grid-scale (SGS) model. The large eddies depend more on the geometry of the system, while the small eddies are more universal. Therefore, the SGS models developed in the context of LES are more universal. By contrast, the turbulence models for RANS have different favourable flow regimes. With the increase in computational power, the application of LES in internal combustion engines becomes more feasible [52].

Comparing to the conventional Reynolds-averaged Navier–Stokes (RANS) approach, the LES usually reproduces more flow structures, eddies, and vortices. This is due to the lower dissipation nature of the SGS models and sometimes the smaller grid size. Usually, the LES is recognized as a more accurate approach. However, the accuracy of the LES is difficult to be validated, especially for the applications of engine combustion in which the results are influenced by many factors. The LES results are based on the spatially averaged quantities, while the RANS results are based on the ensemble-averaged. Special attention is required when comparing the LES results with RANS results or experimental data [52].

Usually, the computational cost of LES is much higher than the RANS simulations, which is counted as one disadvantage of the LES. This is mainly due to the much smaller mesh size used in the LES. Given the same mesh size, the computational costs of LES are usually higher than but about the same magnitude as the ones of RANS simulations. This is particularly true when a detailed reaction mechanism is employed in the simulation of reactive flows since most of the CPU time is spent on solving the stiff ordinary differential equations of the chemical reactions. Sometimes, the RANS simulations could be slower than the LES. For instance, simulations of breathing processes using \(k - \omega\) turbulence model take more CPU time than using LES with dynamic structure model, since it is more difficult for the \(k - \omega\) model to get convergent in solving the transport equations [13, 14]. Thus, the computational cost of LES using moderate mesh size is acceptable for modern engineering applications.

Formulations of the LES Models

To separate the scales, the filtering technique is applied to an arbitrary flow variable defined in the space–time system:

$$\overline{\phi }\left( x \right) = \mathop \int \limits_{V} G\left( {x;y} \right)\phi \left( y \right){\text{d}}y$$
(18.1)

Classical filters include box (top-hat) filter, Gaussian filter, and spectral (sharp cut-off) filter [53]. The flow variable is then decomposed into a resolved part \(\overline{\phi }\) and an SGS part \(\phi ^{\prime}\):

$$\phi = \overline{\phi } + \phi {^{\prime}}$$
(18.2)

The resolved part represents the large-scale flow motion that is solved exactly, while the SGS part represents the small-scale flow motion that needs to be modelled. For the compressible flow, it will be more convenient to consider the Favre-averaged filtered quantities:

$$\tilde{\phi } = \frac{{\overline{\rho \phi } }}{{\overline{\rho }}}$$
(18.3)

Apply the above definition into the momentum equation, the filtered equation can be derived:

$$\frac{{\partial \left( {\overline{\rho }\tilde{u}_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\tilde{u}_{i} \tilde{u}_{j} } \right)}}{{\partial x_{j} }} = - \frac{{\partial \overline{p}}}{{\partial x_{i} }} + \frac{{\partial \overline{\sigma }_{ij} }}{{\partial x_{j} }} - \frac{{\partial \tau_{ij} }}{{\partial x_{j} }} + \overline{F}_{i}^{s} + \overline{F}_{i}^{b}$$
(18.4)

with \(\sigma_{ij}\) the viscous term; \(F^{s}\) the source term due to spray; \(F^{b}\) the body force; and sub-grid stress tensor:

$$\tau_{ij} = \overline{\rho }\left( {\widetilde{{u_{i} u_{j} }} - \tilde{u}_{i} \tilde{u}_{j} } \right)$$
(18.5)

The sub-grid stress tensor contains the sub-grid term that is needed to be modelled, which is the focus of the LES modelling. A variety of sub-grid models have been developed. In the following sections, some representative models are introduced.

Smagorinsky Model

Using the mean gradient assumption, the Smagorinsky model [60] describes the sub-grid stress tensor as a function of strain rate tensor and cell size:

$$\tau_{ij} = - 2\nu_{t} \overline{S}_{ij}$$
(18.6)

The turbulent viscosity

$$\nu_{t} = C_{s}^{2} {\Delta }^{2} \sqrt {S_{ij} S_{ij} }$$
(18.7)

where \({\Delta }\) is the grid filter that is computed from the local cell volume:

$${\Delta } = V^{1/3}$$
(18.8)

\(C_{s}\) is an adjustable model constant. For different flow regimes, different values of \(C_{s}\) should be used, which reduces the robustness of the model. To avoid such a dilemma, a dynamic model is introduced to determine the model constant locally. The method is based on the self-similarity theory of the turbulent flow. Additional to the grid filter \({\Delta }\), another test filter with a length scale \({\hat{\Delta }}\) is considered. Usually, this test filter is twice the grid filter (\({\hat{\Delta }} = 2{\Delta }\)). The sub-grid stress tensor based on the test filter is:

$$T_{ij} = \left( {\widehat{{u_{i} u_{j} }} - \hat{u}_{i} \hat{u}_{j} } \right)$$
(18.9)

The difference between the test-level and double-filtered grid-level sub-grid stress tensor is the Leonard stress term [18]:

$$L_{ij} = T_{ij} - \hat{\tau }_{ij} = \widehat{{\overline{u}_{i} \overline{u}_{j} }} - \hat{u}_{i} \hat{u}_{j}$$
(18.10)

the deviatory part of \(L_{ij}\) is written as:

$$L_{ij} - \frac{1}{3}L_{kk} \delta_{ij} = C_{{s,{\text{dyn}}}} M_{ij}$$
(18.11)

where

$$M_{ij} = 2{\hat{\Delta }}^{2} \widehat{{\left| {\overline{S}} \right|\overline{S}_{ij} }} - 2{\hat{\Delta }}^{2} \left| {\overline{S}} \right|\overline{S}_{ij}$$
(18.12)

Using the least square method, the model constant \(C_{{s,{\text{dyn}}}}\) can be determined locally:

$$C_{{s,{\text{dyn}}}} = \frac{{M_{ij} L_{ij} }}{{M_{kl} M_{kl} }}$$
(18.13)

This is the dynamic Smagorinsky model.

One Equation Viscosity Model

The turbulent viscosity can be modelled by adopting the sub-grid kinetic energy. The sub-grid stress tensor is written as:

$$\tau_{ij} = - 2\nu_{t} \overline{S}_{ij} + \frac{2}{3}k\delta_{ij}$$
(18.14)

in which the turbulent viscosity is modelled as:

$$\nu_{t} = C_{k} k^{1/2} {\Delta }$$
(18.15)

and \(k\) is the sub-grid kinetic energy that is written as:

$$k = \frac{1}{2}\left( {\overline{{u_{i} u_{i} }} - \overline{u}_{i} \overline{u}_{i} } \right)$$
(18.16)

The sub-grid kinetic energy \(k\) is determined by solving its transport equation. The modelled transport equation is given as:

$$\frac{\partial k}{{\partial t}} + \overline{u}_{i} \frac{\partial k}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left( {\frac{{\nu_{t} }}{{\sigma_{k} }}\frac{\partial k}{{\partial x_{i} }}} \right) - \tau_{ij} \frac{{\partial \overline{u}_{i} }}{{\partial x_{j} }} - \varepsilon$$
(18.17)

\(\varepsilon\) is the dissipation rate of the sub-grid kinetic energy \(k\). Its value is determined from:

$$\varepsilon = C_{\varepsilon } k^{3/2} {\Delta }^{ - 1}$$
(18.18)

\(C_{k}\), \(\sigma_{k}\), and \(C_{\varepsilon }\) are model constants.

Dynamic Structure Model

Similar to the dynamic Smagorinsky model, the dynamic structure model [27, 50] is based on an assumed scaling between resolved and sub-grid scales and a mathematical identity that arises. A second filtering operation that is designated the “test”-level filter is conducted. The “grid”-level (\(K\)) and “test”-level (\(\hat{K}\)) turbulent kinetic energies are defined by

$$K = \frac{1}{2}\left( {\widetilde{{u_{i} u_{j} }} - \widetilde{{u_{i} }}\widetilde{{u_{j} }}} \right)$$
(18.19)
$$\hat{K} = \frac{1}{2}\left( {\widehat{{u_{i} u_{j} }} - \widehat{{u_{i} }}\widehat{{u_{j} }}} \right)$$
(18.20)

respectively. The Leonard term relates the test- and grid-level kinetic energies:

$$\hat{K} = K + \frac{1}{2}L_{ii}$$
(18.21)

The “grid”- and “test”-level modelled stress tensor are

$$\tau_{ij} = c_{ij} K$$
(18.22)
$$\hat{\tau }_{ij} = c_{ij} \hat{K}$$
(18.23)

Substituting these models for the two stress tensors into the Germano identity yields

$$L_{ij} = c_{ij} \hat{k} - \widehat{{c_{ij} k}}$$
(18.24)

The sub-grid tensor is then written as:

$$\tau_{ij} = 2k\frac{{L_{ij} }}{{L_{ii} }}$$
(18.25)

Spray Models and Combustion Models for LES

Most of the current spray models and combustion models were developed in the context of RANS. When the LES is employed, some models need to be modified accordingly to keep consistent [52], especially the ones involving turbulent quantities. Currently, adjusting the spray models in the context of LES is rarely discussed. Most of the LES of engine combustion directly adopted the spray models developed in the context of RANS, with the tuning of certain model constants. Most of the adjustment is to tune certain model constants in the spray models, particularly the secondary breakup model. Figure 18.1 shows the measured (symbol) and predicted (lines) liquid penetration length of a non-reactive spray in a constant volume combustion chamber (CVCC). The injector is the ECN spray A. The pressure and temperature in the CVCC at the beginning of fuel injection are 60.5 bar and 829.5 K, respectively. All the simulations use the Kelvin–Helmholtz Rayleigh–Taylor (KH-RT) breakup model, base mesh size of 2 mm, level three adaptive mesh refinement, and level three mesh embedding near the nozzle exit. With all the default model constants, the KH-RT model coupled with RANS successfully reproduces the liquid penetration length [36]. When the turbulence model is switched to LES with the dynamic structure model, the KH-RT model with all the default model constants over-predicted the liquid penetration, as indicated by the green dotted line (“LES1”). When the velocity model constant in the KH model is adjusted from the default value of 0.188 to 5.04, the results of the KH-RT model match the experimental data very well. The gas-phase velocity is utilized in the calculation of the droplet’s drag force. With different turbulence model, the averaged gas-phase velocities are different. This explains why tuning the velocity model constant in the KH model has an evident impact on the spray prediction when the turbulence model is changed from RANS to LES. The liquid penetration at the end of the injector valve opening is over-predicted by the RANS, which is not shown in the results of LES. Stronger fluctuation is observed in the results of LES that is due to its transient nature. Other approaches reported in the literature used much finer mesh [46], design of experiment, and optimization to tune the model constants [39]. The fundamental ideas are the same: adjust the breakup model constants. A more rigorous physics-based approach is expected to avoid the empirical tuning of model constants.

Fig. 18.1
figure 1

Measured (symbol) and predicted (lines) liquid penetration length of a non-reactive spray

Full size image

The other aspects of the spray models also require attention. Bharadwaj et al. [5] derived the filtered equation for two-phase flow, with a focus on the spray source terms in the gas-phase transport equations. With the point source assumption, the spray source term in the transport equation of sub-grid kinetic energy is derived and modelled using a deconvolution method. Different from the RANS approach, this source term could be either sink or source of kinetic energy.

When the LES is considered, usually the turbulent combustion model that involves turbulent fluctuation should be re-developed. KIVA–CHEMKIN model and SAGE model assume that each computational cell is a perfectly stirred reactor [28, 67]. This approach assumes that the turbulence has no direct impact on the chemical kinetics. Sub-grid fluctuation is largely neglected in the formulation; i.e. the model is not dependent on the SGS model. The turbulence effects on the NOx and soot emissions are reflected through the turbulent viscosity in the LES. The same reaction mechanisms and emission models including NOx and soot can be directly applied in LES. Thus, such types of models can be directly implemented into the LES seamlessly [3, 21, 24]. However, some flamelet-based models should be adjusted. For instance, the G-equation model is a turbulent combustion model for premixed combustion, which is based on the flamelet assumption. The G-equation model tracks the flame front of the propagating flame. When a RANS model is employed, the turbulent flame speed is usually computed from Peters’ model [48]:

$$s_{t} = s_{l} + u^{\prime}\left[ { - \frac{{a_{4} b_{3}^{2} }}{{2b_{1} }}{\text{Da}} + \sqrt {\left( {\frac{{a_{4} b_{3}^{2} }}{{2b_{1} }}{\text{Da}}} \right)^{2} + a_{4} b_{3} {\text{Da}}} } \right]$$
(18.26)

where \(s_{l}\) is the laminar flame speed, \(u^{\prime}\) is the root mean square of the turbulent fluctuating velocity; \(a_{4} ,{ }b_{3} ,{ }\) and \(b_{1}\) are model constants. \({\text{Da}}\) is the Damkohler number:

$${\text{Da}} = \frac{{s_{l} l_{t} }}{{u^{\prime}l_{F} }}$$
(18.27)

where \(l_{t}\) is the turbulent length scale; and

$$l_{F} = \frac{{\lambda /c_{p} }}{{\left( {\rho s_{l} } \right)_{u} }}$$
(18.28)

The subscript “u” indicates an unburnt region.

If an LES model is employed, Peters’ model is no longer valid. The new formulation of turbulent flame speed is derived as [49]:

$$s_{t} = s_{l} \left[ {1 - \frac{{b_{3}^{2} C_{\nu } }}{{2b_{1} {\text{Sc}}_{t} }}\frac{{\Delta }}{{l_{F} }} + \sqrt {\left( {\frac{{b_{3}^{2} C_{\nu } }}{{2b_{1} {\text{Sc}}_{t} }}\frac{{\Delta }}{{l_{F} }}} \right)^{2} + \frac{{b_{3}^{2} D_{t} }}{{s_{l} l_{F} }}} } \right]$$
(18.29)

with \({\text{Sc}}_{t}\) the turbulent Schmidt number. \(C_{\nu }\) is the model constant in the formulation of turbulent viscosity in the SGS model.

In a diesel engine, the liquid fuel is injected into the gaseous charge. The bulk liquid fuel atomizes into small-size droplets. The droplets vaporize and the vapour mixes with the gaseous charge. Autoignition occurs in a premixed mixture. After the premixed burn, a turbulent diffusion flame develops, which is called diffusion burn. The laminar flamelet model can be used to model the turbulent diffusion flames. The flamelet timescale (FTS) model, which is a quasi-steady flamelet model coupled with a timescale model, was developed and applied to diesel combustion [21, 22]. The transport equation for the mean mixture fraction and the mixture fraction variance is written as:

$$\frac{{\partial \left( {\overline{\rho }\tilde{\xi }} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\tilde{\xi }\tilde{u}_{j} } \right)}}{{\partial x_{j} }} = - \frac{{\partial \tau_{{u_{j} \tilde{\xi }}} }}{{\partial x_{j} }} + \frac{\partial }{{\partial x_{j} }}\left( {\widetilde{{\rho D\frac{\partial \xi }{{\partial x_{j} }}}}} \right) + \overline{\rho }\widetilde{{\dot{\xi }^{s} }}$$
(18.30)
$$\begin{aligned} \frac{{\partial \left( {\overline{\rho }\widetilde{{\xi^{{{^{\prime\prime}}2}} }}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\widetilde{{\xi^{{{^{\prime\prime}}2}} }}\tilde{u}_{j} } \right)}}{{\partial x_{j} }} = & - 2\tau_{{u_{j} \widetilde{{\xi^{{{^{\prime\prime}}2}} }}}} \frac{{\partial \tilde{\xi }}}{{\partial x_{j} }} + \frac{\partial }{{\partial x_{j} }}\left( {\overline{\rho }\overline{D}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }}} \right) \\ & - 2\overline{\rho }\chi_{{{\text{sgs}}}} + 2\left[ {\widetilde{{\rho \xi \dot{\xi }^{2} }} - \rho \tilde{\xi }\widetilde{{\dot{\xi }^{s} }}} \right] \\ \end{aligned}$$
(18.31)

The flux of the mean of mixture fraction is defined as

$$\tau_{{u_{j} \tilde{\xi }}} = \overline{\rho }\left( {\widetilde{{u_{j} \xi }} - \tilde{u}_{j} \tilde{\xi }} \right)$$
(18.32)

The flux of the variance of mixture fraction is defined as

$$\tau_{{u_{j} \widetilde{{\xi^{{{^{\prime\prime}}2}} }}}} = \overline{\rho }\left( {\widetilde{{u_{j} \xi^{{{^{\prime\prime}}2}} }} - \tilde{u}_{j} \widetilde{{\xi^{{{^{\prime\prime}}2}} }}} \right)$$
(18.33)

The same approach as the dynamic structure model is applied to modelling these flux terms, which are written as a function of the variance of mixture fraction and the corresponding Leonard terms:

$$\tau_{{u_{j} \tilde{\xi }}} = \widetilde{{\xi^{{{^{\prime\prime}}2}} }}\frac{{L_{{u_{j} \xi }} }}{{L_{{\xi^{{{^{\prime\prime}}2}} }} }}$$
(18.34)

The Leonard terms are given as

$$L_{{u_{j} \xi }} = \widetilde{{\overline{\rho }\tilde{u}_{j} \tilde{\xi }}} - \widehat{{\overline{\rho }}}\widehat{{\tilde{u}}}_{j} \widehat{{\tilde{\xi }}}$$
(18.35)
$$L_{{\xi^{{{^{\prime\prime}}2}} }} = \widetilde{{\overline{\rho }\tilde{\xi }\tilde{\xi }}} - \widehat{{\overline{\rho }}}\widehat{{\tilde{\xi }}}\widehat{{\tilde{\xi }}}$$
(18.36)

The sub-grid-scale scalar dissipation rate is given as

$$\chi_{{{\text{sgs}}}} = D\left( {\widetilde{{\frac{\partial \xi }{{\partial x_{i} }}\frac{\partial \xi }{{\partial x_{i} }}}} - \frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}\frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}} \right),$$
(18.37)

which is modelled using a zero-equation model:

$$\chi_{{{\text{sgs}}}} = C\frac{D}{{{\Delta }^{2} }}\widetilde{{\xi^{{{^{\prime\prime}}2}} }}$$
(18.38)

with \(C\) the model constant.

To account for the unsteady effects in diesel combustion, a characteristic timescale is introduced. The rate of change of species i is written as,

$$\frac{{\partial \tilde{Y}_{i} }}{\partial t} = \frac{{\tilde{Y}_{i} - \tilde{Y}_{i}^{{{\text{lib}}}} }}{{\tau_{{{\text{chem}}}} }}$$
(18.39)

\(\tilde{Y}_{i}^{{{\text{lib}}}}\) is the mass fraction calculated from the flamelet library. \(\tau_{{{\text{chem}}}}\) is the characteristic timescale describing the duration that the current flamelet proceeds towards its steady state. Its value is evaluated from a one-step irreversible reaction for diesel combustion:

$$\tau_{{{\text{chem}}}} = A^{ - 1} Y_{{{\text{fuel}}}}^{{{0}{\text{.75}}}} Y_{{O_{2} }}^{ - 1.5} \exp \left( {\frac{{E_{a} }}{{{\text{RT}}}}} \right)$$
(18.40)

The mixed-mode combustion model was developed for diesel combustion [23]. The model considers a flame that is consists of three modes: a kinetically controlled (KIN) mode, a quasi-steady homogenous (QSH) mode, and a quasi-steady flamelet (QSF) mode. By introducing two combustion indices \(\alpha\) and \(\gamma\) that are used to identify the local combustion regimes, the final reaction rate is written as:

$$\widetilde{{\dot{\omega }}}_{i} = \alpha \widetilde{{\dot{\omega }}}_{i}^{{{\text{KIN}}}} + \left( {1 - \alpha } \right)\left[ {\gamma \widetilde{{\dot{\omega }}}_{i}^{{{\text{QSH}}}} + \left( {1 - \gamma } \right)\frac{{\left( {\tilde{Y}_{i} - \int Y_{i}^{{{\text{FL}}}} p\left( Z \right){\text{d}}Z} \right)}}{{\tau_{{{\text{FL}}}} }}} \right]$$
(18.41)

The first combustion index, \(\alpha\), is used to distinguish the slow-chemistry regime from the fast-chemistry regime, i.e. depending on the chemical timescale. A simple criterion based on the local gas temperature is developed for \(\alpha\):

$$\alpha = {\mathcal{H}}\left( {\frac{T}{{T_{c} }} - 1} \right)$$
(18.42)

with \({\mathcal{H}}\) the Heaviside function and \(T_{c}\) the cut-off temperature. The second combustion index, \(\gamma\), is used to distinguish the quasi-steady homogeneous regime from the quasi-steady diffusion flamelet regime. It is written as a function of scalar dissipation rate, which indicates the local mixture homogeneity:

$$\gamma = \min \left( {1,\frac{\chi }{{\chi_{c} }}} \right)$$
(18.43)

\(\chi\) is the local scalar dissipation rate. \(\chi_{c}\) is the criterion of scalar dissipation rate between the diffusion flamelet regime and the partially premixed regime.

Zhang and Rutland [65, 66] developed a mixing-controlled direct chemistry combustion model for LES of diesel combustion. The SGS scalar dissipation rate is modelled using a similarity term and a scaling factor estimated from the DNS data. The mixing effect is modelled by a mixing timescale based on mixture fraction variance and sub-grid scalar dissipation rate, which ranges \(10^{ - 6} \sim 10^{ - 3} s\) for different engine conditions. A kinetic timescale based on the specific internal energy is introduced, which shows improvements over the conventional single-species-based timescale.

The progress variable approach coupled with the dynamic Smagorinsky model was used to simulate an HCCI engine [25, 64]. Good comparisons with experimental pressure traces were achieved. Thickened flame model is similar to the progress variable approach and G-equation model, which artificially increases the flame thickness to represent the turbulence effect on the premixed flamelet [12]. The model has been implemented into LES and applied to simulate the multiple cycles of a spark-ignited premixed charge compression ignition (PCCI) engine [61]. Coherent flamelet was adopted in LES of diesel combustion [30, 32] and spark-ignited engines [51, 63].

Applications

LES is a powerful tool to predict unsteady phenomena in a turbulent flow, which are associated with some critical phenomena in engine combustion, such as combustion instability, turbulent mixing, and turbulence-chemistry interactions. LES has been applied to engine combustion since three decades ago [3, 15, 22, 24, 25, 27, 28, 29, 37, 51, 61, 68] especially for unsteady phenomena prediction such as cyclic variation [1, 20, 62, 63] and fluctuations in spray [26]. But it is not ready for engine optimization yet due to its high computational cost, and immature physical models. A series of workshops on “LES for Internal Combustion Engine Flows” (LES4ICE) has been organized to advance LES applications for engine simulation.

In the section, the LES with dynamic structure model is applied to simulate the combustion processes of a heavy-duty diesel engine. The results are compared with the ones of the RANS with RNG (Renormalization Group) \(k - \varepsilon\) model [19]. The engine is based on a Cummins N-series production, which is a single-cylinder, direct injection (DI), four-stroke diesel engine. The engine has been extensively investigated experimentally [6,7,8, 11, 16, 17, 33,34,35, 40,41,42, 44, 45, 57, 59] and numerically [9, 16, 55, 56, 58]. Table 18.1 lists the configurations of this engine. One engine case, which features low-temperature combustion and early injection, is simulated. Table 18.2 shows the operating conditions of this case.

Table 18.1 Engine configurations
Full size table
Table 18.2 Operating conditions
Full size table

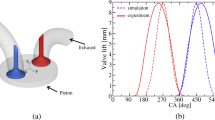
A commercial CFD software CONVERGE is employed in the present study. A real fluid model, the Redlich–Kwong equation of state, was employed. SAGE combustion model with ERC n-heptane mechanism [47] is used. Two different skeletal n-heptane mechanisms, the ERC mechanism [47] and Chalmers mechanism [38], are considered. The ERC reaction mechanism consists of 34 species and 74 reactions, including the mechanism of NO, N2O, and NO2. The Chalmers mechanism consists of 42 species and 168 reactions, including 3 reactions about N and NO. A sector mesh is used. The base mesh size is set to 2 mm. Level three adaptive mesh refinement (AMR) is activated by both temperature gradient and velocity gradient. A level three fixed embedding is applied to refine the meshes near the nozzle exit during the injection process, so that consistent mesh resolution is achieved. Thus, the minimum mesh size is 0.25 mm. Figure 18.2 shows the computational mesh coloured by the velocity magnitude during the spray injection, showing that the spray plume is covered by the fixed embedding. AMR is activated by the high-velocity gradient outside of the fixed embedding regime. The spray is represented by a collection of tetradecane droplet parcels. O’Rourke’s model [43] is used to describe the turbulent dispersion. The evaporation model used is the Frossling model [2] with n-heptane being the sourced species. To capture the droplet collision, the NTC collision with post-collision outcomes [54] is chosen. The Kelvin–Helmholtz and Rayleigh–Taylor breakup model [4] is used to model the droplet secondary breakup. A uniform droplet size that is the same as the nozzle size is set to all the droplet parcels. Except for the different turbulence models and the different velocity constant in the KH model (c.f., Fig. 18.1), all of the other models and settings in the RANS and LES are the same.

Fig. 18.2
figure 2

Computational mesh

Full size image

Figure 18.3 shows the comparison of measured and predicted pressure trace and heat release rate. Good agreements are achieved in all the simulations. Two-stage combustion is observed in the present case, with a cool flame followed by a diffusion flame. This is very typical for diesel combustion with early injection [10]. Both simulations using the ERC mechanism predict the cool flame and the main combustion earlier than the experimental data, while the combustion predicted by the LES using Chalmers mechanism is later than the experimental data. Thus, the chemical kinetics is more critical for the prediction of averaged thermodynamic properties, such as pressure trace and heat release rate. Relatively, the different turbulence models have minor impacts on the predictions of these averaged quantities. The predictions of these properties mainly depend on the prediction of combustion phasing. The turbulence model influences the prediction of mixing and turbulent flame speed. With the same ERC mechanism, the LES and RANS predict almost identical timing of the cool flame, which is dominated by the chemical kinetics. The LES predicted the main combustion is earlier than the one predicted by the RANS. The peak pressure predicted by the LES matches the experimental data better.

Fig. 18.3
figure 3

Measured and predicted pressure trace and heat release rate

Full size image

Figure 18.4 shows the comparison of measured and predicted liquid and vapour distributions. The left column is the Planar LIF image of fuel vapour. The middle column is the results of LES. The right column is the results of RANS. The droplet parcels are indicated as blue dots in the simulation results. The contour plot indicates the concentration of the fuel vapour (C7H16). Reasonable agreements between the simulations and measurements are achieved. Overall, both LES and RANS over-predict the vapour penetration and liquid penetration after −20° degrees ATDC. This may be due to the inaccurate rate of injection profile used in these simulations. As shown in Fig. 18.2, with different velocity model constant in the KH model, the LES and RANS predict similar liquid penetration. Therefore, during the early stage (before −16° ATDC), the difference between LES and RANS is minor, since the spray injection and evaporation are the dominant factors for the development of the mixing and flow structure. Unstable flow phenomena are observed in both LES and RANS results. This is due to the KH instability of the spray breakup process. After −16° ATDC, an evident difference in vapour distribution predicted by LES and RANS is observed. The results of RANS show a smoother distribution in space than the ones of LES, due to its time-averaged nature. The LES results are more chaotic.

Fig. 18.4
figure 4

Comparison of measured and predicted liquid and vapour distributions

Full size image

Figure 18.5 shows the comparison of measured and predicted OH and temperature distributions at −11 and −10° ATDC, at which the ignition occurs. The left column is the Planar LIF image of OH and temperature. The middle and right columns are the results of LES and RANS, respectively. The contour plots in blue from simulations indicate the OH mole fraction. The contour plots in green from simulations indicate the temperature. The formation of OH is well-captured by the simulations, especially the LES. According to the pressure trace shown in Fig. 18.3, the ignition events predicted by the LES and RANS are earlier than the measurement. Thus, the predicted in-cylinder temperature is higher than the experimental data. The primary distribution of OH and temperature is similar between LES and RANS. The ones predicted by LES show more complex topology and structure than the ones predicted by RANS. Comparing to the RANS results, higher OH concentration and temperature are observed in the LES results, which is consistent with the pressure trace shown in Fig. 18.3. The different turbulence models predict different gas flow fields, first the velocity and consequently the other passive scalars. Assuming the same temperature and pressure, the difference in the fuel–air mixture predicted by the different turbulence models will lead to different ignition events.

Fig. 18.5
figure 5

Comparison of measured and predicted OH and temperature distributions

Full size image

Figure 18.6 shows the scatter plot of the equivalence ratio and temperature at −14, −12, −11, and −10° ATDC. Each data point indicates one computational cell. The colour of the point indicates the mole fraction of OH. Note that the equivalence ratio is calculated from all the C, H, and O in all the components, including CO2 and H2O. At −14° ATDC, the two simulations show very similar distributions in the spaces of equivalence ratio and temperature. At −12° ATDC, the LES results show more cells having an equivalence ratio of 0.5–2.0, which is favourable for autoignition. Additionally, some cells with an equivalence ratio of 3.0–4.0 in the LES results have a higher temperature than the RANS results, which implies that pyrolysis reactions occur earlier in the LES results than the RANS results. This explains that the combustion predicted by the LES is earlier than the one predicted by RANS, as shown in Fig. 18.3. At −11° ATDC, both simulations show the ignition events. In the LES results, the high-temperature cells form a separated island from the low-temperature cells. The RANS results show a smoother and more homogeneous distribution between the low temperature and high temperature. This phenomenon can also be seen at −10° ATDC when the major combustion occurs and the flame temperature reaches more than 2000 K.

Fig. 18.6
figure 6

Scatter plot of equivalence ratio and temperature at −14°, −12°, −11°, and −10° ATDC

Full size image

Figure 18.7 shows the iso-surface of the temperature of 1100 K at −12° ATDC, as well as the droplets. The left and right ones are the results of LES and RANS, respectively. The iso-surface is coloured by the vorticity magnitude. It shows that the flame is initialized near the liner. The flame front predicted by the RANS is much smoother than the one predicted by the LES. The vorticity magnitude on the flame front is much more homogeneous than the LES results which show many wrinkles on the iso-surface. This implies that the LES predicts a more detailed flow structure than the RANS. These wrinkles increase the total surface area of the flame front. Although the LES predicts a larger surface area, there is no evidence showing that the turbulent flame speed predicted by the LES with SAGE model is higher than the one predicted by the RANS, as shown in the profiles of pressure trace and heat release rate. This is consistent with the finding in an LES study of turbulent jet ignition [31].

Fig. 18.7
figure 7

Iso-surface of temperature (1100 K) at −12° ATDC. The iso-surface is coloured by vorticity magnitude

Full size image

Future and Challenges

Significant progress has been made in the research of LES, including fundamental research and application. Many aspects of the LES are getting mature, including sub-models, numerical schemes, numerical set-ups, and analysis. Applications of LES in engine combustions are rapidly growing. However, there are still a lot of challenges remaining. Particularly, the spray models, wall function, and combustion models should be redeveloped and evaluated in the framework of LES.

Although the LES is more sensitive to design changes [52], its unsteady nature prevents it from design evaluations. Given the same engine design, the performance parameters of single-cycle engine combustion from LES vary. When a certain design is changed, it is very difficult to determine whether the changes in single-cycle LES results are due to the design change or its unsteady nature. To obtain meaningful LES results for the evaluation of design performance, multiple cycle LES is required. The total number of cycles should be great enough to be statistically significant, e.g. 20 cycles. This will lead to very expensive computational costs. Thus, LES is still not a good option for optimization of the engine design.