Post-buckling Analysis of FG Columns Based on Weak Finite Element Formulation

Abstract

The post-buckling analysis of a FG column subjected to a free-end axial compressive load where the axis is aligned along the Cartesian x has been carried out. The study has been performed for different free-end angles, and the findings are reported in detail. The material is graded in the radial direction which consists of different materials at inner and outer surface of the cross section. Owing to the solution complexity pertaining to the use Cartesian system, the θ, S plane polar coordinate system has been used to obtain the simple governing nonlinear differential equation. The Galerkin’s finite element formulation has been used to obtain the solution of the FG columns subjected to different loading conditions. For the purpose of analysis, the following loading conditions namely concentrated tip load, uniformly distributed load along the axis, and a uniformly varying load along the axis have been considered. The load parameters are presented for various end slopes, and the results are compared with published results.

1 Introduction

Functionally graded (FG) materials due to their tailor-made properties find their application in aerospace, automobile, and marine sectors. Structural member when subjected to axial compressive load deforms in the transverse direction which reaches a large value known as buckling when the load becomes critical. The buckling deformation is nonlinear and takes place in a very short time and is called as post-buckling. Hence, the post-buckling behavior of members subjected to axial compressive loads is an important area of study. The elastic stability of isotropic and homogeneous structures is thoroughly studied by Timoshenko and Gere [1]. Sankar [2] proposed an elasticity solution for analysis of FG beams with assumed exponential variation of modulus of elasticity across the thickness. The analysis is based on a simple Euler–Bernoulli beam theory. Chakraborty et al. [3] developed new beam finite element for the analysis of functionally graded materials and the exact solution for static part has been arrived.

Analysis of post-buckling behavior of beam-column structures by stochastic finite elements has been performed by Graham-Brady and Schafer [4]. Aydogdu [5] analyzed the vibration and buckling of simply supported axial FG beams using the semi-inverse method based on Euler–Bernoulli beam theory by varying the Young’s modulus exponentially in the axial direction. Huang and Li [6] studied the effect of radial gradient on buckling loads of elastic FG circular columns taking into account the shear deformation. Li along with co-authors [7, 8] established the closed form relations between buckling loads of FG Timoshenko beams and homogenous Euler–Bernoulli beams by considering the variation of Young’s modulus and Poisson’s ratio in the thickness direction of the beams. Heydari [9] presented the exact analytical solutions for buckling of functionally graded beams with rectangular and annular cross sections and concluded the first buckling mode shape of prismatic FG beam is similar to that of the prismatic homogenous beam. Saljooghi et al. and Ranganathan et al. [10, 11] studied the free vibration and buckling nature of FG beams using kernel particle method and perturbation method. Li et al. [12] investigated the critical buckling loads of FG Levinson beams (FGLBs) in comparison with those of homogeneous Euler–Bernoulli beams considering the through-the-depth material gradient. Alshabatat [13] estimated the buckling capacity of axially compressed FG slender columns using trigonometric function and genetic algorithm for optimizing the volume fractions. Zhang et al. [14] conducted detailed review of stability, buckling, and free vibration analysis of functionally graded structures. The review of literatures suggests that post-buckling behavior of FG columns with through the radial direction gradation of ‘n’ sided polygon cross section has not yet been reported which provides the scope for further work. The polygon cross-sectional metal columns find their application in high-mast poles and stadium light poles, and hence, the tall chimneys of power plant may soon adopt to polygon cross section and hence FG polygon cross section are an important consideration. The present work is devoted on detailed study of the post-buckling behavior of FG columns with through the radius material gradation.

2 Theoretical Formulation

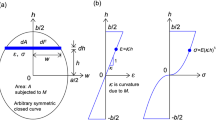
The geometry of functionally graded fixed-free hollow column considered for the study is shown in Fig. 1a. The θ, S plane polar coordinate system has been used to obtain the simple governing nonlinear differential equation. The coordinate frame of axes as shown in Fig. 1a with measuring distance s along the axis of the column from the origin O. The cross section of the FG column is a n-sided polygon displayed as shown in Fig. 1b. The governing exact differential equation of the deflection curve of the fixed-free column given as follows [1]

$${\text{EI}}\frac{{{\text{d}}\theta }}{{{\text{d}}s}} + Py = 0$$

(1)

Fig. 1

Schematic representation of a fixed-free cantilever FG column b cross section of the FG column

Differentiating Eq. (1) with respect to ‘s’ and using the relation $\frac{{{\text{d}}y}}{{{\text{d}}s}} = \sin \theta$, Eq. (1) reduces to

$${\text{EI}}\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}s^{2} }} + P\sin \theta = 0$$

(2)

Non-dimensionalizing Eq. (2) using the relation $\xi = \frac{s}{L}$, where L = length of column [15]

$$\theta^{\prime\prime} + \lambda f \sin \theta = 0$$

(3)

where $\theta^{\prime\prime} = \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\xi^{2} }}$, the axial coordinate ξ = 0 at free end and ξ = 1 at fixed end, ${\lambda }$, f are the buckling load and load parameter, respectively, given by

• $\lambda = \frac{{PL^{2} }}{{{\text{EI}}}}$, a tip load at free end ‘P’ and f = 1

• $\lambda = \frac{{qL^{3} }}{{{\text{EI}}}}$, a uniformly distributed axial load (UDL) ‘q’ and f = ξ

• $\lambda = \frac{{qL^{3} }}{{2{\text{EI}}}}$ a uniformly varying axial load (UVL) ‘q’ and f = ξ².

Now, expanding the sin θ term in the form of

$${\text{Sin}} \theta = \theta {-}\frac{{\theta^{3} }}{3!} + \frac{{\theta^{5} }}{5!}{-}\frac{{\theta^{7} }}{7!} + \cdots = \theta { }\left( {1{-}{ }\frac{{\theta^{2} }}{3!}{ } + \frac{{\theta^{4} }}{5!}{ }{-}{ }\frac{{\theta^{6} }}{7!}{ } + { } \cdots } \right) = f_{1} \theta$$

(4)

where Eq. (3) reduces to $\theta^{\prime\prime} + \lambda ff_{1} \theta = 0$.

The material property ${\varvec{E}}$ for FG column varies continuously in the radial direction of the cross section according to the power law [10]

$$E = E\left( r \right) = { }E_{{r_{1} }} + \left( {\frac{{r - r_{1} }}{{r_{2} - r_{1} }}} \right)^{m} \left( {E_{{r_{2} }} - E_{{r_{1} }} } \right)$$

(5)

where r₁ and r₂ are internal and external radius of the cross section. Since the cross section of the FG column is a ${\varvec{n}}$-sided polygon shape of radius ‘r’ whose moment of inertia I is given by [16] while the flexural rigidity $\left( {{\varvec{EI}}} \right)$ is given below

$$I = n{ }\int\limits_{0}^{{\frac{{\uppi }}{n}}} {\int\limits_{{\frac{{r_{1} \cos \left( {\frac{\pi }{n}} \right)}}{\cos \phi }}}^{{\frac{{r_{2} \cos \left( {\frac{\pi }{n}} \right)}}{\cos \phi }}} {r^{3} } } {\text{d}}r{\text{ d}}\phi {\text{ and EI}} = n\int\limits_{0}^{{\frac{{\uppi }}{n}}} {\int\limits_{{r_{1} {\text{cos}}\left( {\frac{\pi }{n}} \right)/\cos \phi }}^{{r_{2} {\text{cos}}\left( {\frac{\pi }{n}} \right)/\cos \phi }} {E\left( r \right)r^{3} } } {\text{d}}r{\text{ d}}\phi$$

(6)

2.1 Finite Element Problem

Equation 4 is solved for large deflection analysis using weighted residual Galerkin’s finite element (FE) method [17]. For such analysis, the following cubic displacement polynomial is assumed over each element as follows

$$\theta_{e} = \alpha_{1} + \alpha_{2} { }\xi + \alpha_{3} \xi^{2} + \alpha_{4} \xi^{3} = \left[ A \right]\left\{ \alpha \right\}_{e}$$

(7)

$$\left[ A \right] = { }\left[ {\begin{array}{*{20}c} 1 & \xi & {\xi^{2} } & {\xi^{3} } \\ \end{array} } \right],{ }\left[ \alpha \right]_{e}^{T} = { }\left[ {\begin{array}{*{20}c} {\alpha_{1} } & {\alpha_{2} } & {\alpha_{3} } & {\alpha_{4} } \\ \end{array} } \right]$$

Defining the nodal parameters $\theta$ and $\theta^{\prime}$, the nodal values $\left\{ \delta \right\}_{e}$ are related to $\left\{ \alpha \right\}_{e}$ by

$$\left\{ \delta \right\}_{{\text{e}}} = \left[ T \right]\left\{ \alpha \right\}_{{\text{e}}}$$

(8)

where

$$\left\{ \delta \right\}_{e}^{T} = \left[ {{ }\begin{array}{*{20}c} {\theta_{1} } & {\theta_{1}^{\prime } } & {\theta_{2} } \\ \end{array} { }\theta_{2}^{\prime } } \right]{\text{ and }}\left[ T \right] = \left[ {\begin{array}{*{20}c} 1 & {x_{1} } & {x_{1}^{2} } & {x_{1}^{3} } \\ 0 & 1 & {2x_{1} } & {3x_{1}^{2} } \\ 1 & {x_{2} } & {x_{2}^{2} } & {x_{2}^{2} } \\ 0 & 1 & {2x_{2}^{2} } & {3x_{2}^{2} } \\ \end{array} } \right]$$

in which x₁ and x₂ are nodal coordinates of respective element with subscripts 1 and 2 denote the two ends of the element and [T] is a transformation matrix

$$\left\{ \alpha \right\}_{e} = \left[ { T } \right]^{ - 1} \left\{ \delta \right\}_{e} ;\; \left\{ \theta \right\}_{e} = \left[ \phi \right]\left\{ \delta \right\}_{e} ; \;\left[ \phi \right] = \left[ { A } \right]\left[ T \right]^{ - 1}$$

(9)

Making use of the above Galerkin’s formulation, Eq. (4) can be written in the residual form with the residue given by

$$R_{e} = \left[ \phi \right]^{\prime \prime } \left\{ \delta \right\}_{e} + \lambda \,f\,f_{1} \left[ \phi \right]\left\{ \delta \right\}_{e}$$

(10)

Extremizing the residual ${\varvec{R}}_{{\varvec{e}}}$ yields the governing equation of the post-buckling problem

$$\frac{\partial }{{\partial \left\{ \delta \right\}_{e} }}\smallint \theta_{e} R_{e} d\xi = 0$$

(11)

$$\left[ K \right]\left\{ \delta \right\} + \lambda \left[ G \right]\left\{ \delta \right\} = 0$$

(12)

where [K] is the stiffness matrix and [G] is the geometric stiffness matrix given by

$$\left[ K \right] = \smallint \left[ \phi \right]^{T} \left[ \phi \right]^{{^{\prime\prime}}} { }d\xi {\text{ and}}\left[ G \right] = \smallint ff_{1} \left[ \phi \right]^{T} \left[ \phi \right]{ }d\xi$$

The function f₁ in geometric stiffness matrix [G] is evaluated using standard iterative method for initial assumed value θ = 0 and maintained accuracy 10^–6. Equation (12) is solved using eigenvalues and eigenvectors solver of MATLAB after imposing the following boundary conditions.

$$\theta^{\prime}\left( {\xi = 0} \right) = 0{\text{ and }}\theta \left( {\xi = 1} \right) = 0$$

(13)

3 Results and Discussions

The FE model-based MATLAB program developed in the earlier sections have been used to predict the behavior of the FG columns. The material properties of the constituent ceramic–metal properties of the FG column are boron nitride ceramic with Young’s modulus ${\varvec{E}}_{{{\varvec{BN}}}} = 19.5\,{\text{GPa}}$ while aluminum metal with Young’s modulus ${\varvec{E}}_{{{\varvec{AL}}}} = 70\,{\text{GPa}}$, respectively. The property variation along the radial cross-sectional direction of cross section for different material parameter $\left( {\varvec{m}} \right)$ is displayed in Fig. 2.

Fig. 2

Young’s modulus gradation through radial director (ceramic to metal)

The first step in the analysis to validate the FE model for which the following are the three types of axial loads are accounted for:

• $\lambda = \frac{{PL^{2} }}{{{\text{EI}}}}$, a tip load at free end P and f = 1

• $\lambda = \frac{{qL^{3} }}{{{\text{EI}}}}$, a uniformly distributed axial load (UDL) q and f = ξ

• $\lambda = \frac{{qL^{3} }}{{2{\text{EI}}}}$ a uniformly varying axial load (UVL) q and f = ξ².

In order to validate the present FE model for accuracy, a uniform cantilever column with n = 100 resembling circular cross sections of isotropic material rich (m = 0) is considered and a parametric study has been carried out and are compared with the pioneering works of Timoshenko and Gere [1] and Rao and Raju [15]. Tables 1 and 2 show such comparisons with the pioneering works, and the entries to the table show that the results are in good agreement with one another. Table 1 shows the results of ratio of nonlinear buckling to linear (critical) buckling (λ/λ_cr)_, x_a/L and y_a/L at various end rotations (β) for 8 elements. 8 element results have converged with closed form solution for tip load at free end. Similarly, Table 2 shows the results of UDL and UVL and critical buckling load values.

Table 1 λ_cr and tip deflection of FG cantilever column subjected to a concentrated tip load

Table 2 λ_cr and tip deflection of FG cantilever column subjected to a uniformly distributed axial load (UDL) and uniformly varying axial load (UVL)

In the present investigation, the post-buckling behavior of FG columns for various material parameters m ranging from (10^–2 to 10²) with (n_CM) for ceramic (at r₁) to metal (at r₂) and (n_MC) metal (at r₁) to ceramic (at r₂) is presented. For such analysis, different regular polygon shapes have been considered and the results are displayed in Fig. 3. The results show that post-buckling (λ) behavior of FG hollow regular polygon column at different material parameters (m) and various end rotations (β) varies from β = 0° to 176°, angle at the top of the column. The increase in end rotation β also increases post-buckling load. Once buckling begins, the structure can withstand maximum load before failure while the withstanding capacity increases with β. As the material parameter m varies from 0 to ∞, the post-buckling load decreases and it may be clearly attributed to the fact of reduced stiffness of the column. The FG column transforms from ceramic rich to metal rich as the m increases whose stiffness is proportional to flexural rigidity (EI) and with I constant E decreases and depicted in Fig. 2. The reverse trend is observed for FG column transforming from metal rich to ceramic rich with increase in m and the same is displayed in Fig. 4. Figure 5 shows the flexural rigidity effect on post-buckling load for different material parameters (m) for a particular end rotation β. Figure 6 shows the influence of different axial loads on the post-buckling load of the column.

Fig. 3

Post-buckling load versus material parameter m for different polygons (ceramic to metal)

Fig. 4

Post-buckling load versus material parameter m for different polygons (metal to ceramic)

Fig. 5

Post-buckling load for different material parameter m at β = 176°

Fig. 6

Post-buckling load variation with material parameter m for different loading conditions

The results show that the post-buckling load increases in the order as tip concentrated load, uniformly distributed load, and uniformly varying load. The above result may serve as reference for designing the structures composed of columns. Figures 7 and 8 show the horizontal deflections at various end rotations for end tip concentrated load, UDL, and UVL. The curve AB is tangent to the horizontal line λ = λ_cr at point A where the deflection is zero. The λ/λ_cr increases when deflection increases up to certain limit, once the FG column reaches the proportional limit (may be curve AB), the resistance to bending of the FG column diminishes drastically and a curve similar to BC and is indicated by a dotted line. The above results are shown in terms of non-dimensional form, so that the changes are not noticed for different polygon shapes. But the post-buckling load increases with increase of number of sides in regular polygon.

Fig. 7

Post-buckling to critical buckling load ratios for tip concentrated load

Fig. 8

Post-buckling to critical buckling load ratios for UDL and UVL

4 Conclusions

The post-buckling behavior of FG column with different polygon cross sections for various material gradation parameters is demonstrated successfully leading to following conclusions:

• The post-buckling load increases with increase of end rotations

• The post-buckling load depends on flexural rigidity and hence the material gradation.

• The λ/λ_cr increases with deflection increasing up to certain limiting value while beyond proportional limit, the post-buckling increases rapidly before failure.

• The post-buckling load is maximum for UVL compared to other loadings.

• The post-buckling behavior can be controlled with the cross section varying from either ceramic to metal or metal to ceramic.

• The post-buckling behavior is also dependent on shape of the cross section.