Keywords

1 Introduction

The first Reciprocating diaphragm pump by the piston’s reciprocating motion to achieve periodic changes in its working cavity volume, reciprocating diaphragm pump has the advantages of high head, self-absorption ability and high efficiency. The head of reciprocating diaphragm pump is not affected by flow and media viscosity. Therefore, reciprocating diaphragm pumps are widely used in mining, fire protection, ships, military and petrochemical fields [1,2,3].

Diaphragm pump belongs to a type of reciprocating pump, and it can be roughly divided into power end and hydraulic end. The hydraulic end consisting of pistons, diaphragm chambers, diaphragms, suction valves and drain valves is the part in contact with the conveying mineral slurry. In the suction process, the suction valve is open and the drain valve is closed. In the drain process, the drain valve is open and the suction valve is closed. The suction and drain valves cooperate with each other to complete a delivery of mineral slurry. Hydraulic end pump valve is a consumable because of its direct contact with the ore slurry. It is often washed by the ore slurry, resulting in its working environment is extremely harsh as a key component. The reliability will directly affect the efficiency of the diaphragm pump and work costs.

In 1968, Adolf of Germany analyzed the force equilibrium of the mass valve, and established the second-order nonlinear non-aligned motion equation of the mass valve core by combining the basic principles of fluid mechanics and continuity conditions. Since then, considering with the reciprocating diaphragm pump basic theory, the mass valve movement law has been studied for a long time. A lot of theoretical models have also proposed to analyze the movement of pump valve, and the formula of valve core movement law and the law of pressure change in the cylinder during inhalation was established. With the development of reciprocating diaphragm pump technology and the expansion of its application field, more works have been carried out. Ling et al. [4, 5] established the elaborated model of the diaphragm pump operating mechanism on the basis of the separated diaphragm pump parameters, and the design process and its destruction basis of the valve core for mass-less pump valve were discussed in detail.

The researches on reciprocating diaphragm pump valve mainly focuse on the analysis of its motion equation, and the normal study of valve gap flow field. The effect of spring stiffness and pretension force on the movement law of valve core has not considered [6]. At present, through experiments and CFD numerical simulation, foreign scholars have studied the flow field characteristics of pump valves in different states and discussed them optimally [7]. The second-order nonlinear differential equation of the pump valve established by Adolf in 1968 can be used to describe the working process after the reciprocating diaphragm pump valve is open. However, the equations can not be employed to describe the process of open and close the valve and the impact of the valve with the lift limiter during movement.

Based on the idea of Taylor series expansion method, the Runge-Kutta method will avoid the interpretation of the original function and simplifies the process of numerical solution of differential equations. It represents the guiding value of a point by means of a function value near a point, and forms the Taylor fraction by linear combination of function values at some special points. Thus, finds the numerical solution of the differential equation [8]. In order to obtain an approximation of the flow field inside the pump valve, the flow field is discrete into a series of special points instead of the continous flow field to establish the algebraic equations of the flow field [9]. Chen and Jaw [10] has improved the turbulence model and introduced a new turbulent energy delivery equation. Liang and Meng [11] established a mathematical model of pump valve motion on the basis of analyzing the movement law of reciprocating diaphragm pump valves. The problem of the single point of the pump valve was sloved as the valve open, and the resluts were verified by compared with that by using the Runge-Kutta method.

The purpose of this paper is to provide reference for the design of the hydraulic end pump valve of the reciprocating diaphragm pump. Under the condition that the study of mass valve is relatively scarce, the motion equation of Adolf mass valve is solved numerically by Runge-Kutta method. The motion law curve of the mass valve in the course of one inhalation is obtained. At the same time, the influences of the structural parameters of the mass valve on the movement law are analyzed and discussed. The kinetic energy for the closed the mass valve is obtained, which provides the precondition for exploring the life of the quality valve later.

2 Dynamics Model of Hydraulic Mass Valve

2.1 Differential Equation of the Mass Valve

The object of this paper is to establish the dynamic characteristics of a quality core spring automatic valve. Because the valve in the process of operation is very complex, it can not be described in a general simple way. Therefore, he dynamic equations of the valve can be obtained by simplified means to ignore some very small factors [12,13,14].

In order to derive the dynamic equation of a mass valve, some assumptions are made as following:

  1. 1)

    Liquid is not compressible;

  2. 2)

    Diaphragm pump components has not deformation during the work process;

  3. 3)

    The liquid cylinder block is always fully filled during works.

Fig. 1.
figure 1

Force analysis of the hydraulic end valve

Full size image

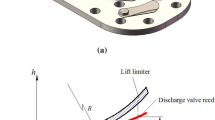
As shown in Fig. 1, the force equilibrium equation on the quality core spring automatic valve can be given by,

$$ P_{2v} A_{v} + F_{j} - G - F_{sv} - P_{1v} A_{v} = \theta \dot{h} + m\ddot{h} $$
(1)

where,

\(P_{1v} ,P_{2v}\) for the valve upper and lower side pressure;

\(F_{j}\) for mechanical friction for valve-guided friction;

\(F_{sv}\) is spring force meanwhile \(F_{sv} = F_{gv} + kh\), \(F_{gv}\) is called the pre-pressure of the spring when the valve is closed;

\(\theta \dot{h}\) represents the resistance of the liquid to the valve. The valve plate velocity is proportional, but the direction and valve plate movement direction is the opposite;

\(m\ddot{h}\) is the inertial force for the valve plate is moving.

Because, \(\theta \dot{h}\) and \(F_{j}\) are much smaller than the other terms, the effects of the two terms can be ignored, we can get,

$$ \phi \Delta P_{v} A_{v} = G + \left( {F_{gv} + kh} \right) + m\ddot{h} $$
(2)

where, in: \(\phi\) in order to take into account the difference in liquid pressure between the valve and the seat of the coefficient introduced, can be approximated to one, \(\Delta P_{v} = P_{2v} - P_{1v}\) is the pressure difference between the upper and lower fluids of the mass valve.

2.2 Nonlinear Dynamics Model of Hydraulic End Mass Valve

In Eq. (2), two unknown quantities were found to be the pressure difference \(\Delta P_{v}\) and valve plate lift \(h\) of the liquid up and down the valve. Therefore, in order to find the lift performance of the mass valve plate, the liquid continuity equation can be introduced to form a closed equation system with Eq. (2). According to the mass valve model shown in Fig. 1 and the classical reciprocating pump mechanism, the continuity equation of the mass valve can be obtained,

$$ Au = q_{v} + A_{v} \dot{h} + \frac{V}{E}\Delta P_{v} $$
(3)

where, \(A\) is the piston area, \(u = R\omega \left( {\sin \varphi + {\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\sin 2\varphi } \right)\) is piston velocity, \(Au\) is the transient flow of diaphragm pump, \(A_{v} \dot{h}\) is valve movement caused by their own flow, \(\frac{V}{E}\Delta P_{v}\) respresnts pressure under the elastic deformation of the cylinder wall and caused by liquid compression for liquid not fully filled, which can be described as changes in liquid volume. \(q_{v}\) is gap flow, and the expression can be given by

$$ q_{v} = \mu \pi d_{v} h\sqrt {2g\frac{{p_{2v} - p_{1v} }}{\rho g}} = hl_{v} \sqrt {\frac{{2\Delta P_{v} }}{\rho \zeta }} $$

where \(\zeta = \frac{1}{{\mu^{2} }}\), and \(\mu\) is called the mass valve flow factor.

Ignoring the deformation the deformation of the pump, the nonlinear differential equations of the hydraulic end mass valve can be expressed as

$$ T^{2} h^{2} \ddot{h} + h^{3} + Ah^{2} - \varepsilon_{1} Bf^{2} + \varepsilon_{1} Cf\dot{h} - \varepsilon_{1} D\dot{h}^{2} = 0 $$
(4)

where,

$$ T^{2} = {m \mathord{\left/ {\vphantom {m k}} \right. \kern-\nulldelimiterspace} k},A = \frac{{G + F_{gv} }}{k},B = \frac{{\rho \zeta \phi A_{v} A^{2} R^{2} \omega^{2} }}{{2kl_{v}^{2} }}, $$
$$ C = \frac{{\rho \zeta \phi A_{v} A^{2} R\omega }}{{2kl_{v}^{2} }},D = \frac{{\rho \zeta \phi A_{v}^{2} }}{{2kl_{v}^{2} }},f = \sin \varphi + \frac{\lambda }{2}\sin 2\varphi . $$

In the case of the number of reciprocating membrane pumps is determined, and the structural parameters of the diaphragm pump and the mass valve can be determined by assuming the flow coefficient is a constant value. Then the coefficients A, B, C, and D in formula (4) can be determined as normal coefficients. The mass valve lift curve can be obtained by solved Eq. (4). The Runge-Kutta method is used to solve Eq. (4), and the nonlinear vibration characterisrics for the diaphragm pump and the mass valve will be discussed.

3 Results and Discussions

3.1 Mass Valve Lift Curve

The basic parameters of the diaphragm pump and valve are given as listed: piston diameter D, piston stroke S, pressure P, punch n, flow Q, crank radius R, connecting rod length L, crank angle velocity, spring stiffness k, valve plate cross-sectional area Av, piston cross-sectional area A, and valve clearance circumference lv. Crank corner \(\varphi = \omega t = 24.63t\) and the linkage ratio \(\lambda = {R \mathord{\left/ {\vphantom {R L}} \right. \kern-\nulldelimiterspace} L} = {{255} \mathord{\left/ {\vphantom {{255} {1700}}} \right. \kern-\nulldelimiterspace} {1700}} = 0.15\). In order to explore the movement law of the valve, the system parameters are taken as follows:

$$ \mu = 0.8,\zeta = {1 \mathord{\left/ {\vphantom {1 {\mu^{2} }}} \right. \kern-\nulldelimiterspace} {\mu^{2} }} = 1.56,\varepsilon_{1} = 1,E = 2.07 \times 10^{11} Pa, $$
$$ T^{2} = \frac{m}{k} = 0.0134,A = \frac{{G + F_{gv} }}{k} = 0.035, $$
$$ B = \frac{{\rho \zeta \phi A_{v} A^{2} R^{2} \omega ^{2} }}{{2kl_{v}^{2} }} = 5.79 \times 10^{{ - 6}} ,C = \frac{{\rho \zeta \phi A_{v} A^{2} R\omega }}{{2kl_{v}^{2} }} = 8.956 \times 10^{{ - 7}} $$
$$ D = \frac{{\rho \zeta \phi A_{v}^{2} }}{{2kl_{v}^{2} }} = 2.129 \times 10^{ - 6} , $$
$$ f = \sin \varphi + \frac{\lambda }{2}\sin 2\varphi = \sin 24.63t + 0.075\sin 49.26t. $$

So, Eq. (5) can be solved by using the Runge-Kutta method. and the relationship between valve lift and time can be obtained. In order to make the curve universal, the lift curve in the second cycle of inhalation is taken as shown in Fig. 2.

Fig. 2.
figure 2

Valve lift and velocity curve during the second cycle of inhalation

Full size image

As can be seen in Fig. 2, the inhalation process begins at 0.255 s, and the valve starts to start at 0.264 s delaying by 9 ms. In time t = 0.314 s to reach the maximum lift in the entire inhalation process, at this time the velocity is 0. When the cylinder begins to inhale the slurry, the spring is compressed and spring force is also increased. So the valve in the opening instant to reach the maximum velocity after the deceleration movement. As the suction process enters the second half, the pressure of the liquid surface under the valve plate is getting smaller and smaller, the inhalation motion is entered the last half of process, and the valve core is closeed at the last moment t = 0.383 s. The valve plate begins to be shocked at t = 0.378 s, in this time the velocity is 0.0485 m/s, which will be used as the initial value of the impact velocity in subsequent studies.

Fig. 3.
figure 3

The movement of the valve core under different stiffness

Full size image

3.2 Performance Parameter Analysis

The result curve calculated by numerical calculation shows that the valve plate is in a state of quivering for some time when the valve is started, and the velocity curve can obviously detect this problem. Therefore, the parameters of the valve are studied in depth for this problem.

When the parameters of the diaphragm pump is operating, the seat is fixed, only the valve core is in a state of motion. The parameter variable that affects the movement of the valve core is spring stiffness.

In the process of diaphragm pump inhalation, due to the instant of the suction valve opening, the inhalation pipe slurry has a certain impact on it. The spring force belongs to the recess force, resulting in the opening of the valve plate instantly produced a jitter phenomenon. Figure 3(a) shows that during the suction of the diaphragm pump, the lift of the valve core has a certain controlled by the spring stiffness. The peak of valve plate jitter is 1.812 mm at k = 4600 N/m, and the peak at k = 5600 N/m is 1.388 mm. The greater the spring stiffness, the more inhibition there is to jitter when the valve core is open. Meanwhile the smaller the displacement jitter peak of the valve core.

In Fig. 3(b), the mass valve core velocity tremor lasts to t = 0.286 s at stiffness k = 4600 N/m. Oppositely, in the curve of k = 5600 N/m, the velocity is smooth at t = 0.275 s, so the phenomenon of valve plate velocity oscillation is effected by spring stiffness positively. However, the spring stiffness and the shock kinetic energy of the valve plate at the end of the closing of the suction process are reflected by figure(c), which means to jitter phenomenon has been reduced when the valve core is opene. But it is not desirable to increase the stiffness of the spring, the service life of the valve will be reduced due to the shock kinetic energy at the close is over large.

3.3 Valve Structure Parameters and Lift Relationship

Under certain conditions of flow, the relationship between valve structure parameters and valve plate lift is explored. The instantaneous flow of the diaphragm pump is:

$$ Q = Au = AR\omega \left( {\sin \varphi + \frac{\lambda }{2}\sin 2\varphi } \right) $$
(5)

Where: \(A\) is the piston cross-section, \(u\) is the piston velocity, \(\omega\) is the crank velocity, and \(\varphi = \omega t\) is the crank corner. During the suction of the diaphragm pump, the flow curve through the hydraulic end suction valve is shown in the figure below.

Fig. 4.
figure 4

Instantaneous traffic

Full size image

The instantaneous flow of the diaphragm pump approximates the sine function as shown as Fig. 4, the relationship between valve structure parameters and ascension is studied. Figure 5 shows that the relationship between the geometric parameters of the valve plate and the lift of the valve plate is different at a certain flow rate. It can be seen that when the valve core cross-sectional area is 0.0079 m2 in Fig. 5(a). The maximum value of the valve plate lift is 2.673 mm, however, the cross-sectional area is increased to 0.0113 m2, the maximum lift is 3.187 mm. The flow through the valve seat pores is certain, in order to ensure that the liquid filled in the cylinder conditions, the larger the cut-off area of the valve plate, the higher the required lift. In conclusion, when the perimeter of the valve seat pores and the flow through the suction valve is certain, the larger the section area of the valve core, the higher the lift.

Fig. 5.
figure 5

Valve structure parameters and valve plate lift relationship curve

Full size image

On the contrary, in Fig. 5(b). The perimeter of the valve seat clearance is increased from 0.4084 m to 0.4712 m, and the maximum lift of the valve plate was 3.438 mm, 3.179 mm, 2.988 mm. I.e. the intercept area of the valve core was unchanged, and the lift required for the valve plate was smaller in order to meet the liquid-filled cylinder conditions at certain times. Under the same conditions, when the two structural coefficients of the valve plate are adjusted,the two different results are produced. So the ratio of the two parameters can be studied to further find some suitable structural parameter ratios of the valve.

Fig. 6.
figure 6

Valve lift curve at the different circumference of seat holes

Full size image

In Fig. 6, cross-sectional coordinates for the valve plate cut-off area and valve seat pore circumverse ratio, that is, \({{A_{v} } \mathord{\left/ {\vphantom {{A_{v} } {l_{v} }}} \right. \kern-\nulldelimiterspace} {l_{v} }}\), from the relationship between the maximum valve plate lift and the ratio is almost positive linear relationship. When the ratio is greater, the larger the valve plate cut-off area meanwhile, the larger the lift is required valve plate in a certain flow situation. This result is consistent with the results shown in Fig. 5.

4 Conclusions

Based on the mechanism of the mass valve of the diaphragm pump, as well as the basic principles of mechanics and fluid mechanics, the nonlinear motion differential equation with mass valve core is derived. In order to explore the movement trajectory of the mass valve plate in the process of inhalation, the numerical solution of the second-order nonlinear non-alignment normal differential equation is calculated by numerical calculation method. The main conclusions obtained are as follows:

  1. 1.

    A nonlinear dynamic model of the mass valve of the diaphragm pump is established. And the lift curve of the mass valve of the typical diaphragm pump is calculated by the Runge-Kutta method.

  2. 2.

    When the diaphragm pump mass valve core is opened, the jitter phenomenon is appeared obviously in a short period of time after opening. And this calculation result is very similar to the actual observed results.

  3. 3.

    Under the condition that the flow rate is maintained, the lift of the mass valve plate is inversely proportional to its cross-sectional area and proportional to the pore circamation of the seat. As the ratio of the cross-sectional area of the mass valve core to the pore of the seat increases, the higher the lift is required for the mass valve core under the same operating conditions.

  4. 4.

    The jitter phenomenon of mass valve is inhibited by increasing the stiffness of the spring will inhibit the jitter of the mass valve to some extent, but the seat to withsand more impact kinetic will be allowed when closed. Which will have a certain negative impact on the life of the mass valve.