Keywords

1 Introduction

In the past few decades, a great deal of efforts have been taken to accurately position the crane and rapidly reduce payload sway. Typical underacted systems are the crane systems projected to achieve, meaning that the number of independent control inputs is not more than the degrees of freedom (DOFs) [1,2,3,4,5]. The tower crane, enjoying outstanding advantages such as simple structure, convenient installation, low cost, high payload capacity and low energy consumption, is a most extensively used equipment for transporting freights at the construction site [6,7,8]. Nevertheless, on account of its unavoidably complicated disturbance, high nonlinearity, and strong underactuation, the design of the tower crane’s control system is so far both complicated and challenging. Taking the tower crane’s system parameters for example, it is hard to measure them owing to their complicated effect factors. Apart from that, such external disturbances as gust wind also need to be noted owing to its major influence on the stability of the tower crane system. For example, the gust wind may impose an additional payload swing angle. Therefore, we shall take robustness into sufficient consideration in view of its presence of disturbances.

To solve the problems mentioned above, several control methods such as adaptive control [6, 9,10,11], fuzzy logic control [12, 13] and neural network control [14, 15] have been put forward for the sake of reducing the bounded parametric uncertainties. Furthermore, the powerful robustness as well as the capacity to address unmodeled uncertainties, parametric uncertainties, and external disturbances with driving the sliding surface into 0 is the best known factors of the sliding mode control (SMC) method. As a result, a variety of SMC methods such as integral SMC [16], nonlinear SMC [17, 18], adaptive SMC [17, 19], neural network SMC [20, 21] have been designed for tower crane systems. Recently, several disturbance observer-based control methods have been presented [22,23,24,25] to fight off the disturbance effect on the tower crane systems in an even better fashion, which indicate that the disturbance observer-based methods can be used to improve the robustness of the tower crane systems.

However, the tower crane systems’ existing control methods are mostly proposed and made an analysis on the basis of the linearized crane model. And this model will differ from the original crane model distinctively if its state variable is not approximate to the equilibrium point. In this sense, it may affect the control performance so much so that the tower crane’s stability may be under the influence. Moreover, the positive response aroused by the disturbance are absolutely ignored by the robust control method mentioned above because these methods regard the disturbance as mere detrimental factor, and therefore eliminate it directly. However, we shall note that disturbances may also have certain positive influences [26, 27] given that the fact of mistaking deletion the helpful disturbance may assist us in reflecting the disturbance influence on the tower crane system and thus find an approach to make the most of the helpful disturbance. As a result, given the uncertain or unknown feature of the disturbances, we shall observe them in a nonlinear way in order to evaluate them correctly. After that, a disturbance effect indicator (DEI) shall be specially designed in order to make a distinction between the helping disturbances and the harmful ones based on the estimated disturbances. At the last step, a DEI and the estimated disturbance information will be incorporated into the controller design.

The rest of this paper is indicated as below. In Sect. 2, the problem formulation, including the analysis of the error dynamic mel of 4-DOF tower crane systems as well as the control objective are carried out. In Sect. 3, the main results, embracing design of the nonlinear disturbance observer, introduction of the disturbance effect indicator, and design of the DESMC method, are provided. Several simulation results are illustrated in Sect. 4. The main work of this paper is concluded in Sect. 5.

2 Problem Formulation

2.1 Error Dynamic Model

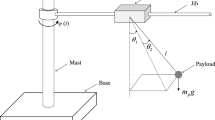
Control problem of positioning, sway reduction together with inevitable disturbances is taken into account for tower crane systems (shown in Fig. 1), whose dynamical equations are presented as follows:

$$ \begin{aligned} & \left[ {m_{p} \left( {S_{1}^{2} C_{2}^{2} + S_{2}^{2} } \right)l^{2} + 2m_{p} xlC_{2} S_{1} + J + \left( {M_{t} + m_{p} } \right)x^{2} } \right]\ddot{\varphi } - m_{p} lS_{2} \ddot{x} - m_{p} l^{2} C_{1} C_{2} S_{2} \ddot{\theta }_{1} \\ & + \,m_{p} l\left( {C_{2} x + lS_{1} } \right)\ddot{\theta }_{2} + 2\left( {M_{t} + m_{p} } \right)x\dot{x}\dot{\varphi } + 2m_{p} lC_{1} C_{2} x\dot{\varphi }\dot{\theta }_{1} - m_{p} lS_{2} \left( {2\dot{\varphi }S_{1} + \dot{\theta }_{2} } \right)x\dot{\theta }_{2} \\ & + \,2m_{p} lS_{1} C_{2} \dot{\varphi }\dot{x} + m_{p} l^{2} S_{21} C_{2}^{2} \dot{\varphi }\dot{\theta }_{1} + m_{p} l^{2} S_{1} S_{2} C_{2} \dot{\theta }_{1}^{2} + m_{p} l^{2} C_{1}^{2} S_{22} \dot{\varphi }\dot{\theta }_{2} + 2m_{p} l^{2} C_{1} S_{2}^{2} \dot{\theta }_{1} \dot{\theta }_{2} \\ & = \,F_{\varphi } - F_{r\varphi } + d_{\varphi } \\ \end{aligned} $$
(1)
$$ \begin{aligned} & - m_{p} lS_{2} \ddot{\varphi } + \left( {M_{t} + m_{p} } \right)\ddot{x} + m_{p} lC_{1} C_{2} \ddot{\theta }_{1} - m_{p} lS_{1} S_{2} \ddot{\theta }_{2} - \left( {M_{t} + m_{p} } \right)x\dot{\varphi }^{2} \\ & - 2m_{p} lC_{1} S_{2} \dot{\theta }_{1} \dot{\theta }_{2} - m_{p} lC_{2} \left[ {S_{1} \left( {\dot{\varphi }^{2} + \dot{\theta }_{1}^{2} + \dot{\theta }_{2}^{2} } \right) + 2\dot{\varphi }\dot{\theta }_{2} } \right] = F_{x} - F_{rx} { + }d_{x} \\ \end{aligned} $$
(2)
$$ \begin{aligned} & - m_{p} l^{2} C_{1} C_{2} S_{2} \ddot{\varphi } + m_{p} lC_{1} C_{2} \ddot{x} + m_{p} l^{2} C_{2}^{2} \ddot{\theta }_{1} - m_{p} lC_{1} C_{2} \left( {x + lS_{1} C_{2} } \right)\dot{\varphi }^{2} \\ & - 2m_{p} l^{2} C_{2} \left( {\dot{\varphi }C_{1} C_{2} + \dot{\theta }_{1} S_{2} } \right)\dot{\theta }_{2} + m_{p} glS_{1} C_{2} = {0} \\ \end{aligned} $$
(3)
$$ \begin{aligned} & m_{p} l\left( {C_{2} x + lS_{1} } \right)\ddot{\varphi } - m_{p} lS_{1} S_{2} \ddot{x} + m_{p} l^{2} \ddot{\theta }_{2} + 2m_{p} lC_{2} \dot{x}\dot{\varphi } + m_{p} l\left( {xS_{1} S_{2} - lC_{1}^{2} S_{2} C_{2} } \right)\dot{\varphi }^{2} \\ & + \,2m_{p} l^{2} C_{1} C_{2}^{2} \dot{\varphi }\dot{\theta }_{1} + m_{p} l^{2} \dot{\theta }_{1}^{2} S_{2} C_{2} + m_{p} glC_{1} S_{2} = {0} \\ \end{aligned} $$
(4)

where the corresponding system variables, parameters and symbols are illustrated in Table 1.

With a series of experimental measurement, the detailed model of the friction torque and the friction force can be calculated as [1, 19, 22]

$$ F_{r\varphi } = F_{r\varphi 1} \tanh \left( {\rho_{\varphi } \dot{\varphi }} \right) + F_{r\varphi 2} \left| {\dot{\varphi }} \right|\dot{\varphi } $$
(5)
$$ F_{rx} = F_{rx1} \tanh \left( {\rho_{x} \dot{x}} \right) + F_{rx2} \left| {\dot{x}} \right|\dot{x} $$
(6)

where \(F_{r\varphi 1}\), \(F_{r\varphi 2}\), \(F_{rx1}\), \(F_{rx2}\), \(\rho_{\varphi }\) and \(\rho_{x}\) standing for friction-related parameters.

For simplicity, Eqs. (1)–(4) are written in the following compact form:

$$ {\varvec{M}}\left( {\varvec{q}} \right)\user2{\ddot{q}} + {\varvec{C}}\left( {{\varvec{q}},\dot{\user2{q}}} \right)\dot{\user2{q}} + {\varvec{G}}\left( {\varvec{q}} \right) = \user2{u + F}^{ * } $$
(7)

wherein \({\varvec{q}}\left[ {\varphi \, x \, \theta_{1} \, \theta_{2} } \right]^{T} \in {\mathbb{R}}^{4}\) stands for the state vector, \({\varvec{M}}\left( {\varvec{q}} \right) \in {\mathbb{R}}^{4 \times 4}\) refers to the inertial matrix, \({\varvec{C}}\left( {{\varvec{q}},\dot{\user2{q}}} \right) \in {\mathbb{R}}^{4 \times 4}\) represents the Coriolis-centripetal matrix, \({\varvec{G}}\left( {\varvec{q}} \right) \in {\mathbb{R}}^{4}\) denotes the gravity vector, \({\varvec{u}} \in {\mathbb{R}}^{4}\) refers to the control input vector, \({\varvec{F}}^{ * } \in {\mathbb{R}}^{4}\) represents the disturbance vector. The detailed expressions for \({\varvec{M}}\left( {\varvec{q}} \right)\), \({\varvec{C}}\left( {{\varvec{q}},\dot{\user2{q}}} \right)\), \({\varvec{G}}\left( {\varvec{q}} \right)\), \({\varvec{u}}\), and \({\varvec{F}}^{ * }\) are omitted due to space limitation.

Equations (3) and (4) reflect the coupling relationship between the actuated jib/trolley motion and the unactuated payload swing motion, and the only way to eliminate the unactuated payload swing angles is to make the best of the coupling relationship. For this purpose, Eq. (7) is divided into the following two parts:

$$ {\varvec{M}}_{11} \user2{\ddot{q}}_{1} + {\varvec{M}}_{12} \user2{\ddot{q}}_{2} + {\varvec{C}}_{11} \dot{\user2{q}}_{1} + {\varvec{C}}_{12} \dot{\user2{q}}_{2} = {\varvec{u}}_{1} + {\varvec{F}}_{1}^{*} $$
(8)
$$ {\varvec{M}}_{12} \user2{\ddot{q}}_{1} + {\varvec{M}}_{22} \user2{\ddot{q}}_{2} + {\varvec{C}}_{21} \dot{\user2{q}}_{1} + {\varvec{C}}_{22} \dot{\user2{q}}_{2} + {\varvec{G}}_{2} = {\varvec{F}}_{2}^{*} $$
(9)

where \({\varvec{q}}_{1} = \left[ {\varphi \, x} \right]^{T}\) represents the actuated state vector, \({\varvec{q}}_{2} = \left[ {\theta_{1} \, \theta_{2} } \right]^{T}\) refers to the unactuated state vector. Due to space limitation, the detailed expressions for \({\varvec{M}}_{11}\), \({\varvec{M}}_{12}\), \({\varvec{C}}_{11}\), \({\varvec{C}}_{12}\), \({\varvec{F}}_{1}^{*}\), \({\varvec{M}}_{22}\), \({\varvec{C}}_{21}\), \({\varvec{C}}_{22}\), \({\varvec{G}}_{2}\), and \({\varvec{F}}_{2}^{*}\) are omitted.

Table 1. Variables, parameters, and symbols of the 4-DOF tower crane system
Full size table
Fig. 1.
figure 1

Schematic diagram of the 4-DOF tower crane system

Full size image

It is easy to obtain that \(\left| {{\varvec{M}}_{22} } \right| > 0\), hence, (9) can be rewritten as follows:

$$ \user2{\ddot{q}}_{2} = - {\varvec{M}}_{22}^{ - 1} {\varvec{M}}_{12} \user2{\ddot{q}}_{1} - {\varvec{M}}_{22}^{ - 1} {\varvec{C}}_{21} \dot{\user2{q}}_{1} - {\varvec{M}}_{22}^{ - 1} {\varvec{C}}_{22} \dot{\user2{q}}_{2} - {\varvec{M}}_{22}^{ - 1} {\varvec{G}}_{2} + {\varvec{M}}_{22}^{ - 1} {\varvec{F}}_{2}^{*} $$
(10)

It follows from (8) and (10) that

$$ \user2{\overline{M}\ddot{q}}_{1} \user2{ + \overline{C}}_{1} \dot{\user2{q}}_{1} + \overline{\user2{C}}_{2} \dot{\user2{q}}_{2} = {\varvec{u}}_{1} + {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{G}}_{2} + {\varvec{F}}_{1}^{*} - {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{F}}_{2}^{*} $$
(11)

where

$$ \begin{gathered} \user2{\overline{M} = M}_{11} - {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{M}}_{12} \hfill \\ \overline{\user2{C}}_{1} = {\varvec{C}}_{11} - {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{C}}_{21} \hfill \\ \end{gathered} $$
$$ \overline{\user2{C}}_{2} = {\varvec{C}}_{12} - {\varvec{M}}_{12} - {\varvec{M}}_{22}^{ - 1} {\varvec{C}}_{22} $$

To further facilitate the following controller design, we define the positioning error vector \({\varvec{e}}\) as

$$ {\varvec{e}} = \left[ {\begin{array}{*{20}c} {\varphi - \varphi_{d} } & {x - x_{d} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {e_{\varphi } } & {e_{x} } \\ \end{array} } \right]^{T} $$
(12)

wherein \(e_{\varphi }\) and \(e_{x}\) refer to the jib and the trolley positioning errors, respectively.

Additionally, we introduce the following sliding surface as

$$ {\varvec{s}} = {\varvec{e}}{ + }\user2{\lambda \dot{e}} = \left[ {\begin{array}{*{20}c} {s_{1} } & {s_{2} } \\ \end{array} } \right]^{T} $$
(13)

wherein \({\varvec{\lambda}} \in {\mathbb{R}}^{2 \times 2} = diag\left( {\begin{array}{*{20}c} {\lambda_{1} } & {\lambda_{2} } \\ \end{array} } \right)\) stands for the positive definite diagonal control matrix.

From Eqs. (11)–(13), it is straightforward to obtain the error dynamic model of the 4-DOF tower crane system as follows:

$$ \user2{\overline{M}\lambda }^{ - 1} \dot{\user2{s}} = {\varvec{u}}_{1} + {\mathbf{X}}_{1} + {\mathbf{X}}_{2} $$
(14)

where \({\mathbf{X}}_{1}\) stands for the bounded measurable vector, and \({\mathbf{X}}_{2}\) refers to the lumped disturbance vector, which are detailed expressed as

$$ \begin{aligned} & {\mathbf{X}}_{1} = - \overline{\user2{C}}_{1} \dot{\user2{q}}_{1} - \overline{\user2{C}}_{2} \dot{\user2{q}}_{2} + \user2{\overline{M}\lambda }^{ - 1} \dot{\user2{e}} + {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{G}}_{2} \\ & {\mathbf{X}}_{2} = {\varvec{F}}_{1}^{*} - {\varvec{M}}_{12} {\varvec{M}}_{22}^{ - 1} {\varvec{F}}_{2}^{*} \\ & \left\| {{\mathbf{X}}_{2} } \right\| \le {\rm N} \\ \end{aligned} $$
(15)

It is easy to conclude that \(\left\| {\overline{\user2{M}}} \right\| \ne 0\), hence, we can simplify (14) as

$$ \dot{\user2{s}} = {\varvec{u}}_{1}^{*} + {\mathbf{X}}_{1}^{*} + {\mathbf{X}}_{2}^{*} $$
(16)

where

$$ \begin{aligned} & {\varvec{u}}_{1}^{*} = \varvec{\lambda} \varvec{\overline{M}}^{ - 1} {\varvec{u}}_{1} \\ & {\mathbf{X}}_{1}^{*} = \varvec{\lambda} {\varvec{\overline{M}}}^{ - 1} {\mathbf{X}}_{1} \\ & {\mathbf{X}}_{2}^{*} = {\varvec{\lambda}} {\varvec{\overline{M}}}^{ - 1} {\mathbf{X}}_{2} \\ \end{aligned} $$

wherein \({\varvec{u}}_{1}^{*}\), \({\mathbf{X}}_{1}^{*}\), and \({\mathbf{X}}_{2}^{*}\) stands for the new control input vector, the new bounded measurable vector, and the new lumped disturbance vector, respectively.

Assumption 1 [1, 6, 8, 11, 19, 22]:

Actually, the payload is always kept beneath the jib/trolley, hence, the payload swings are always remained within the following scopes:

$$ \left| {\theta_{1} } \right| < \frac{\pi }{2}, \, \left| {\theta_{2} } \right| < \frac{\pi }{2} $$
(17)

Assumption 2 [26, 27]:

The lumped disturbance vector \({\mathbf{X}}_{2}^{*}\) and its first time derivative \({\dot{\mathbf{X}}}_{2}^{*}\) are both bounded, and \({\mathbf{X}}_{2}^{*}\), \(d_{\varphi }\), \(d_{x}\) converge to 0 as time approach infinity, which can be mathematically expressed as follows:

$$ \left\| {{\mathbf{X}}_{2}^{*} } \right\| < \beta , \, \left\| {{\dot{\mathbf{X}}}_{2}^{*} } \right\| < \alpha , \, \mathop {\lim }\limits_{t \to \infty } {\mathbf{X}}_{2}^{*} = 0, \, \mathop {\lim }\limits_{t \to \infty } d_{\varphi } = 0, \, \mathop {\lim }\limits_{t \to \infty } d_{x} = 0 $$
(18)

wherein \(\beta\) and \(\alpha\) refer to the upper bounds of \({\mathbf{X}}_{2}^{*}\) and \({\dot{\mathbf{X}}}_{2}^{*}\), respectively.

2.2 Control Objective

The final goal is to transport the payload to the desired location quickly and steadily, in the face of uncertain/unknown dynamics and external disturbances. However, as claimed above, arising from the inherent underactuated nature of crane systems, the payload cannot be controlled directly. Therefore, we divide the control objective into two parts:

  1. 1)

    Positioning: drive the jib/trolley to the desired angle/position, which can be repressed as

    $$ \mathop {\lim }\limits_{t \to \infty } \varphi = \varphi_{d} , \, \mathop {\lim }\limits_{t \to \infty } x = x_{d} $$
    (19)

    with \(\varphi_{d}\) as well as \(x_{d}\) standing for the desired jib slew angle and the desired trolley location, respectively.

  2. 2)

    Payload swing reduction: reduce the payload swing angles, i.e.

    $$ \mathop {\lim }\limits_{t \to \infty } \theta_{1} = 0, \, \mathop {\lim }\limits_{t \to \infty } \theta_{2} = 0 $$
    (20)

3 Main Results

The overall sliding model control framework is illustrated in this section. Firstly, to estimate the lumped disturbance precisely, a nonlinear disturbance observer is deliberately constructed. Then, a new disturbance effect indicator (DET) is defined to distinguish beneficial disturbances from bad ones. Finally, a novel sliding mode control method is provided by employing the estimated disturbance information and the introduced DEI.

3.1 Nonlinear Disturbance Observer Design

First and foremost, the observation error vector the lumped disturbance \({\mathbf{X}}_{2}^{*}\) is introduced as follows:

$$ {\tilde{\mathbf{X}}}_{2}^{*} = {\mathbf{X}}_{2}^{*} - {\hat{\mathbf{X}}}_{2}^{*} $$
(21)

with \({\hat{\mathbf{X}}}_{2}^{*}\) referring to the estimate vector of \({\mathbf{X}}_{2}^{*}\), \({\tilde{\mathbf{X}}}_{2}^{*}\) standing for the observation error vector.

Subsequently, we construct the following auxiliary function based on the form of (15):

$$ {\dot{\varvec{\Gamma }}}_{{1}} = - {\varvec{L}}{{\varvec{\Gamma}}}_{{1}} + {\varvec{L}}\left( { - {\varvec{u}}_{1}^{*} - {\mathbf{X}}_{1}^{*} - {{\varvec{\Gamma}}}_{2} } \right) $$
(22)

where \({\varvec{L}} \in {\mathbb{R}}^{2 \times 2} = diag\left( {\begin{array}{*{20}c} {L_{1} } & {L_{2} } \\ \end{array} } \right)\) stands for the positive definite observation gain matrix, and \({{\varvec{\Gamma}}}_{2}\) is constructed as follows:

$$ {{\varvec{\Gamma}}}_{2} = {\varvec{Ls}} $$
(23)

The estimate vector \({\hat{\mathbf{X}}}_{2}^{*}\) is then defined as

$$ {\hat{\mathbf{X}}}_{2}^{*} ={\varvec{\Gamma }}_{{1}} +{\varvec{\Gamma }}_{2} $$
(24)

Theorem 1:

The estimate vector and observation error are all the time maintained within the permittable scopes by using the nonlinear disturbance observer (22)–(24), which can be mathematically described as

$$ \left\| {{\hat{\mathbf{X}}}_{2}^{*} } \right\| \le {\rm P}_{1} , \, \left\| {{\tilde{\mathbf{X}}}_{2}^{*} } \right\| \le {\rm P}_{2} $$
(25)

with \({\rm P}_{1}\) and \({\rm P}_{2}\) referring to upper bounds of the estimate vector \({\hat{\mathbf{X}}}_{2}^{*}\) and the observation error vector \({\tilde{\mathbf{X}}}_{2}^{*}\), respectively. In addition, the observation error vector \({\tilde{\mathbf{X}}}_{2}^{*}\) converges to zero when time approach infinity, in the sense that

$$ \mathop {\lim }\limits_{t \to \infty } {\tilde{\mathbf{X}}}_{2}^{*} = 0 $$
(26)

Proof: From (16), (22)–(24), one can obtain that

$$ \begin{aligned} {{\dot{\hat{\mathbf{X}}}}}_{2}^{*} & ={\dot{\varvec{\Gamma }}}_{{1}} + {\dot{\varvec{\Gamma }}}_{2} \\ & \;{ = } - {\varvec{L}}{{\varvec{\Gamma}}}_{{1}} + {\varvec{L}}\left( { - {\varvec{u}}_{1}^{*} - {\mathbf{X}}_{2}^{*} - {{\varvec{\Gamma}}}_{2} } \right){\mathbf{ + }}\user2{L\dot{s}} \\ & \;{ = } - {\varvec{L}}{{\varvec{\Gamma}}}_{{1}} + {\varvec{L}}\left( {{\mathbf{X}}_{2}^{*} - \dot{\user2{s}} - {{\varvec{\Gamma}}}_{2} } \right){\mathbf{ + }}\user2{L\dot{s}} \\ & \;{ = } - {\varvec{L}}{\hat{\mathbf{X}}}_{2}^{*} \user2{ + L}{\mathbf{X}}_{2}^{*} \\ \end{aligned} $$
(27)

It follows from (27) that

$$ \begin{aligned} {\hat{\mathbf{X}}}_{2}^{*} & ={\hat{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + {\varvec{e}}^{{ - {\varvec{L}}t}} \int_{0}^{t} {{\varvec{L}}{\mathbf{X}}_{2}^{*} {\varvec{e}}^{{{\varvec{La}}}} da} \\ & \; \le {\hat{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + {\varvec{e}}^{{ - {\varvec{L}}t}} {\varvec{L}}\beta \int_{0}^{t} {{\varvec{e}}^{{{\varvec{La}}}} da} \\ & \; \le {\hat{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + \beta \\ & \; \Rightarrow \left\| {{\hat{\mathbf{X}}}_{2}^{*} } \right\| \le \left\| {{\hat{\mathbf{X}}}_{2}^{*} \left( 0 \right)} \right\| + \beta \\ \end{aligned} $$
(28)

By solving (27), we can also conclude that

$$ \begin{aligned} {\tilde{\mathbf{X}}}_{2}^{*} & ={\tilde{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + {\varvec{e}}^{{ - {\varvec{L}}t}} \int_{0}^{t} {{\dot{\mathbf{X}}}_{2}^{*} {\varvec{e}}^{{{\varvec{La}}}} da} \\ & \; \le {\tilde{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + {\varvec{e}}^{{ - {\varvec{L}}t}} \alpha \int_{0}^{t} {{\varvec{e}}^{{{\varvec{La}}}} da} \\ & \; \le {\tilde{\mathbf{X}}}_{2}^{*} \left( 0 \right){\varvec{e}}^{{ - {\varvec{L}}t}} + {\varvec{L}}^{ - 1} \alpha \\ & \; \Rightarrow \left\| {{\tilde{\mathbf{X}}}_{2}^{*} } \right\| \le \left\| {{\tilde{\mathbf{X}}}_{2}^{*} \left( 0 \right)} \right\| + \left\| {{\varvec{L}}^{ - 1} } \right\|\alpha \\ \end{aligned} $$
(29)

From (29), as time approach infinity, the observation error vector can be calculated as follows:

$$ \mathop {\lim }\limits_{t \to \infty } \left\| {{\tilde{\mathbf{X}}}_{2}^{*} } \right\| \le \left\| {{\varvec{L}}^{ - 1} } \right\|\alpha $$
(30)

\(\left\| {\varvec{L}} \right\| \gg \alpha\) is selected in this paper, on which basis, it can be obtained that

$$ \mathop {\lim }\limits_{t \to \infty } \left\| {{\tilde{\mathbf{X}}}_{2}^{*} } \right\| = 0 \to \mathop {\lim }\limits_{t \to \infty } \left\| {{\hat{\mathbf{X}}}_{2}^{*} } \right\| = 0 $$
(31)

3.2 Disturbance Effect Indicator

As is illustrated in [26], the time-varying disturbances will give rise to the directional property, which has a essentially vital impact on the transient performance of the tower crane system. If the direction of the disturbance is in accordance with the desired motion, the disturbance may have the potential for enhancing the control performance. As a consequence, it is of crucial significance to thoroughly study the relationship between the disturbance influence and the stability/control performance of the controlled system. Here, we give the definition of disturbance effect based on the introduced DEI, which is provided as follows.

Definition 1:

For the tower crane error model (16), the DEI is constructed as follows:

$$ {\varvec{\chi}} = {\text{sgn}} \left( {{\varvec{s}} \circ {\hat{\mathbf{X}}}_{2}^{*} } \right) = \left[ {\begin{array}{*{20}c} {\chi_{1} } & {\chi_{2} } \\ \end{array} } \right]^{T} \in {\mathbb{R}}^{2} $$
(32)

wherein \(\circ\) stands for the element product, based on which, we define the disturbance effect on the error system (16) as

$$ \left\{ \begin{gathered} \chi_{i} > 0:{\text{Disturbance}}\,{\text{effect}}\,{\text{is}}\,{\text{detrimental}} \hfill \\ \chi_{i} < 0:{\text{Disturbance}}\,{\text{effect}}\,{\text{is}}\,{\text{beneficial}} \hfill \\ \chi_{i} = 0:{\text{Disturbance}}\,{\text{effect}}\,{\text{is}}\,{\text{nill,}}\,\,i = 1,2 \hfill \\ \end{gathered} \right. $$
(33)

As we can see from Definition 1, disturbances have negative and positive impacts on the active suspension system. If \(\chi_{i} = 0\), which means disturbances make no difference; if \(\chi_{i} > 0\) and \(\chi_{i} < 0\), disturbances of the system are detrimental and beneficial, respectively. Definition 1 is provided referring to whether the sign of disturbances is in line with the designed motion, and thus it is indispensable to employ the beneficial disturbances to improve the control performance.

3.3 A Novel Sliding Mode Control Method Design and Stability Analysis

First of all, we construct the following non-negative function as follows:

$$ V\left( t \right) = \frac{1}{2}{\varvec{s}}^{T} {\varvec{s}} $$
(34)

Taking the time derivative of (34), and together with the result in (14), one has

$$ \begin{aligned} \dot{V}\left( t \right) & = {\varvec{s}}^{T} \dot{\user2{s}} \\ & \; = {\varvec{s}}^{T} \left( {{\varvec{u}}_{1}^{*} + {\mathbf{X}}_{1}^{*} + {\mathbf{X}}_{2}^{*} } \right) \\ \end{aligned} $$
(35)

Based on the form of (35), we propose the novel sliding mode control method as follows:

$$ {\varvec{u}}_{1}^{*} = - {\varvec{k}}_{p} {\varvec{s}} - {\varvec{k}}_{s} {\text{sgn}} \left( {\varvec{s}} \right) - \left\| {{\varvec{k}}_{u} {\varvec{q}}_{2} } \right\|{\varvec{s}} - {\hat{\mathbf{X}}}_{2}^{*} \circ \Theta \left( {\varvec{\chi}} \right) $$
(36)

with \({\varvec{k}}_{p} = diag\left( {k_{p1} , \, k_{p2} } \right)\) and \({\varvec{k}}_{s}\) standing for positive control gain matrices, \({\text{sgn}} \left( {\varvec{s}} \right) = \left[ {{\text{sgn}} \left( {s_{1} } \right) \, {\text{sgn}} \left( {s_{2} } \right)} \right]^{T}\), \(\Theta \left( {\varvec{\chi}} \right){ = }diag\left[ {\Theta \left( {\chi_{{_{1} }} } \right), \, \Theta \left( {\chi_{2} } \right)} \right]\), with \(\Theta \left( {\chi_{i} } \right), \, i = 1, \, 2\) defined as

$$ \Theta \left( {\chi_{i} } \right) = \left\{ \begin{gathered} 1,{\text{ if }}\chi_{i} \ge 0 \hfill \\ 0,{\text{ if }}\chi_{i} < 0 \hfill \\ \end{gathered} \right., \, i = 1, \, 2 $$
(37)

Additionally, it is easy to conclude from (36) and (37) that

$$ {\varvec{u}}_{1} = {\varvec{\lambda}}^{ - 1} \overline{\user2{M}}\left[ { - {\varvec{k}}_{p} {\varvec{s}} - {\varvec{k}}_{s} {\text{sgn}} \left( {\varvec{s}} \right) - \left\| {{\varvec{k}}_{u} {\varvec{q}}_{2} } \right\|{\varvec{s}} - {\hat{\mathbf{X}}}_{2}^{*} \circ \Theta \left( {\varvec{\chi}} \right)} \right] $$
(38)

Theorem 2:

The designed novel sliding mode control method (38) can drive the jib slew angle and the trolley displacement to their desired locations, moreover, simultaneously eliminate the payload swing angles, in the sense that

$$ \begin{gathered} \mathop {\lim }\limits_{t \to \infty } \left[ {\varphi \, x \, \theta_{1} \, \theta_{2} } \right]^{T} = \left[ {\varphi_{d} \, x_{d} \, 0 \, 0} \right]^{T} \hfill \\ \mathop {\lim }\limits_{t \to \infty } \left[ {\dot{\varphi } \, \dot{x} \, \dot{\theta }_{1} \, \ddot{\theta }_{2} } \right]^{T} = \left[ {0 \, 0 \, 0 \, 0} \right]^{T} \hfill \\ \end{gathered} $$
(39)

Proof: The detailed proof is omitted which is also available upon request.

3.4 Simulation Results and Analysis

In this section, for the purpose of better testing the superior control performance, the designed sliding mode control method, the PD control method [28] and the adaptive control method [6] are chosen as the comparative methods.

After carful tuning, the control gains for all the three control methods are provided in Table 2.

Fig. 2.
figure 2

Simulation results of the designed controller, PD controller, and adaptive controller

Full size image

The system parameters of the 4-DOF tower crane system are provided as follows:

$$ \begin{aligned} & M_{t} = 3.5\,{\text{kg,}}m_{p} = 1\,{\text{kg,}}l = 0.6\,{\text{m, }}F_{r\varphi 1} = 4.4{, }F_{r\varphi 2} = - 0.5{,} \\ & \rho_{\varphi } = 100{,}F_{rx1} = 4.4{,}F_{rx2} = - 0.5{,}\rho_{x} = 100 \\ \end{aligned} $$

In addition, the initial state vector is set as zero, which can be expressed as

$$ \varphi \left( 0 \right) = 0{\text{ deg, }}x\left( 0 \right) = 0{\text{ m, }}\theta_{1} \left( 0 \right) = 0{\text{ deg, }}\theta_{2} \left( 0 \right) = 0{\text{ deg}} $$

Moreover, the desire jib slew angle and trolley position are set as follows:

$$ \varphi_{d} = 45{\text{ deg, }}x_{d} = 1{\text{ m}} $$
Table 2. Control gains
Full size table

The simulation results of the PD control method, the adaptive control method, and the designed sliding mode control method are plotted in Fig. 2. As far as we can observe from Fig. 2, with similar positioning errors (all within 0.02° and 0.001 m) and transportation time (all within 6 s), the payload swing angles of the designed sliding mode control method can be better suppressed compared with those of the PD control method and the adaptive control method. Furthermore, we can also notice that the payload still swings back and forth after the jib and the trolley stop for the PD control method as well as the adaptive control method, while the payload is payload is almost static for the designed sliding mode control method. In addition, the energy consumption of the designed DESMC method is further less that of the comparative control methods. Therefore, we can arrive at a conclusion that the designed sliding mode control method can achieve superior control performance, which is also directly obtained from these simulation results.

4 Conclusion

In this paper, in the presence of model uncertainties and external disturbances, a novel sliding mode control method is designed for the 4-DOF tower crane system. First of all, a nonlinear disturbance observer is constructed to precisely observe the lumped disturbance, and subsequently the sliding mode control method is proposed derived from the defined DEI and the estimated disturbance information. It should be pointed out that, in contrast to completely considering the disturbance as bad element of existing control methods for tower crane systems, the designed sliding mode control method takes best advantages of the beneficial disturbance effect, triggering superior control performance. As a consequence, the proposed sliding mode control method can address the inevitable disturbance in a more wise way. The benefit of the proposed sliding mode control method is tested by simulation results.