Investigation of Maneuvering Characteristics of High-Speed Catamaran Using CFD Simulation

Abstract

Many studies have been done to estimate the maneuvering characteristics of commercial ships. Studies on a high-speed catamaran, there was a great number of theoretical, numerical studies, and experimental investigation, most of them have focused on the resistance performance. In addition, a CFD (Computational Fluid Dynamics) method has become a possible tool to predict hydrodynamics. This study focuses on predicting hydrodynamic maneuvering characteristics of high-speed catamaran by utilizing RANS (Reynold-Averaged Navier-Stokes) solver. The Delft 372 catamaran model was selected as the target hull to analyze hydrodynamic characteristics. Due to the high-speed condition and changeable attitude, the motion of the catamaran was complex. The comparisons of the obtained CFD results including the free surface effects in resistance performance with experimental data were shown a relatively good agreement and it could demonstrate that the presented method could be used for predicting hydrodynamic coefficients of high-speed catamaran. Then virtual captive model tests were performed to obtain hydrodynamic coefficients. The lower-order Fourier coefficients were applied to get the hydrodynamic coefficients in dynamic motion. The linear fitting to Fourier coefficients was observed very well using least square method in the harmonic motion.

1 Introduction

The demand for high-speed catamaran has been increasing significantly in recent years for variety of purposes such as passenger, military, and commercial applications. Studies on high-speed catamaran, there was a great number of theoretical, numerical studies, and experimental investigation, however, most of them have focused on the resistance performance and seakeeping performance. Broglia et al. (2011) simulated to analyze the interference phenomena between monohull with focus on its dependence on the Reynold number using CFD numerical method. The flow around a high-speed vessel in both catamaran and monohull configuration was observed, in addition, the wave patters, wave profiles, streamlines, surface pressure, and velocity fields were analyzed. In addition, they performed an experimental investigation of hull interference effects on the total resistance by changing the distance between monohull of a catamaran in calm water in 2014. On the other hand, the seakeeping investigation for high-speed catamaran has been done by this author in order to emphasize the influence of Froude on the maximum response of the vertical ship motions and the role of the nonlinear effects both on the ship motions and on the added resistance. Wave resistance for high-speed catamaran was investigated by Moraes et al. (2004), they applied two methods were the slender-body theory and the 3D panel method using Shipflow software to estimate the effects of catamaran hull spacing included the effects of shallow water on the wave resistance component.

Regarding CFD simulation for estimating hydrodynamic characteristics, Su et al. (2012) utilized RANS numerical method to predict the motion and analyze the hydrodynamic performance of planning vessels at high speed. Liu et al. (2018) simulated a virtual captive model tests for KCS (KRISO Container Ship) using CFD to estimate linear and nonlinear hydrodynamic coefficients in the 3rd-order Abkowiz model. After that maneuvering simulation was predicted. Applying CFD in marine vehicles using STAR-CCM+ (Hajivand and Mousavizadegan 2015), OpenFOAM (Islam and Soares 2018), and Ansys FLUENT (Nguyen et al. 2018) have been done for predicting maneuvering characteristics.

This paper focuses on estimating the maneuvering characteristics of Delft 372 catamaran at high-speed. Ansys FLUENT 20.1 is used for solving RANS equation. Resistance performance is conducted in order to validate the numerical method. The comparisons of obtained results in resistance performance with experimental data were demonstrated that the presented numerical method was appropriate. Therefore, virtual captive model tests as static drift, pure sway, pure yaw, and combined pure yaw with drift test is conducted in order to obtain hydrodynamic coefficients. The Fourier series is applied to analyze hydrodynamic coefficients in harmonic motion. Especially, the coupling coefficients are found at combined pure yaw with drift angle.

2 Governing Equations and Turbulence Modeling

The homogenous multiphase Eulerian fluid approach is adopted in this study to describe the interface between the water and air, mathematically. Assumption, the flow around the ship is incompressible. The governing equations that need to be solved are the mass continuity equation and momentum equations, which are given in Eqs. (1) and (2) respectively.

$$ \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{i} }} = 0 $$

(1)

$$ \frac{{\partial \overline{{u_{i} }} }}{\partial t} + u_{j} \frac{{\partial \overline{{u{}_{i}}} }}{{\partial x_{j} }} = - \frac{1}{\rho }\frac{\partial p}{{\partial x_{i} }} + \nu \frac{{\partial^{2} \overline{{u_{i} }} }}{{\partial x_{i} \partial x_{j} }} - \frac{{\partial \tau_{ij} }}{{\partial x_{j} }} + \overline{{f_{i} }} $$

(2)

where $u_{i}$ and $u_{j}$ are the average velocity components; $p$ is the average pressure; $\nu$ is the kinematic viscosity; $x_{i}$ and $x_{j}$ are the $i^{th}$ and $j^{th}$ coordinates in the fluid domain respectively; and $\rho$ is the water density; $\tau_{ij} = \overline{{u^{\prime}_{i} u^{\prime}_{j} }}$ is so-called the Reynolds stress tensor; $u^{\prime}_{i}$ and $u^{\prime}_{j}$ are the fluctuating components; $f_{i}$ is the external forces.

In order to capture the wave pattern of the free surface, the volume of fluid (VOF) method is implemented. A transport equation in Eq. (3) is then solved for the advection of this scalar quantity, using the velocity files obtained from the solution of the Navier-Stokes equations at the last time step.

$$ \frac{\partial q}{{\partial t}} + \vec{\nabla }\left( {q\vec{u}} \right) = 0 $$

(3)

Equation (3) gives the volume fraction $q$ for each phase in all computation cell where $\sum\limits_{k = 1}^{2} {q_{k} = 1}$; $u$ is the velocity; $\nabla$ is the gradient.

Furthermore, a $k - \omega$ SST (Shear Stress Transport) model turbulence model is applied to consider the viscous effects. In this turbulence model, $k$ is the turbulence kinetic energy and $\omega$ is the dissipation rate of the turbulent energy. The two equation model of a $k - \omega$ SST is given by the following:

$$ \frac{\partial k}{{\partial t}} + \overline{u}_{i} \frac{\partial k}{{\partial x_{i} }} = P_{k} - \beta^{*} \omega k + \frac{\partial }{{\partial x_{i} }}\left( {\left( {\nu + \sigma_{k} \nu_{t} } \right)\frac{\partial k}{{\partial x_{i} }}} \right) \, $$

(4)

$$ \frac{\partial \omega }{{\partial t}} + \overline{u}_{i} \frac{\partial \omega }{{\partial x_{j} }} = \frac{\gamma }{{\mu_{t} }}P_{k} - \beta^{*} \omega^{2} + \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\nu + \sigma_{\omega } \nu_{t} } \right)\frac{\partial \omega }{{\partial x_{i} }}} \right] + 2\left( {1 - F_{1} } \right)\frac{{\sigma_{\omega 2} }}{\omega }\frac{\partial k}{{\partial x_{i} }}\frac{\partial \omega }{{\partial x_{i} }} $$

(5)

3 Case Study and Coordinate System

The candidate ship presented in this study is Delft 372 catamaran model with symmetrical demi-hulls shape that originally used in TU-Delft by Van’t Veer (1988). The model hull of Delft 372 catamaran is depicted in Fig. 1 and the main particulars are given in Table 1.

Fig. 1.

Delft 372 catamaran geometry

Table 1. Main particular of Delft 372 catamaran

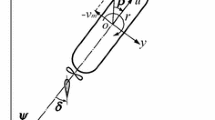
Two right-hand coordinate system are adopted to define the kinematic and hydrodynamic forces acting on the Delft 372 catamaran as shown in Fig. 2. The earth-fixed coordinate system o₀–x₀y₀ is set up to define the ship motion. The body-fixed coordinate system o–xy is used for computing the hydrodynamic forces. The origin is located at the intersection of the waterline plane and the center-line plane at the mid-ship section. The equation of motion for maneuvering ship in 3DOF become:

$$ \begin{aligned} & m(\dot{u} - vr - x_{G} r^{2} ) = X \\ & m(\dot{v} + ur + x_{G} \dot{r}) = Y \\ & \dot{I}_{z} \dot{r} - mx_{G} (\dot{v} + ur) = N \\ \end{aligned} $$

(6)

where m is ship mass; u, v, and r are the surge velocity, sway velocity, and yaw rate, respectively; $\dot{u}$, $\dot{v}$, and $\dot{r}$ are the corresponding surge acceleration, sway acceleration, and angular acceleration; $I_{z}$ is the moment of inertia about the z-axis; $X$, $Y$ and $N$ are the resultant forces acting on ship in surge force, sway force, and yaw moment, respectively; $U$ is the ship speed defined as $U = \sqrt {u^{2} + v^{2} }$; $\beta$ is the drift angle defined by $\beta = \tan^{ - 1} \left( {{{ - v} \mathord{\left/ {\vphantom {{ - v} u}} \right. \kern-\nulldelimiterspace} u}} \right)$.

Fig. 2.

Coordinate system

In addition, the hydrodynamic forces acting on the ship hull are expressed as the below equation:

$$ \begin{aligned} & X_{H} = X_{0} + X_{u} u + X_{uu} u^{2} + X_{uuu} u^{3} + X_{vv} v^{2} + X_{rr} r^{2} + X_{vr} vr \\ & Y_{H} = Y_{{\dot{v}}} \dot{v} + Y_{{\dot{r}}} \dot{r} + Y_{v} v + Y_{vvv} v^{3} + Y_{r} r + Y_{rrr} r^{3} + Y_{vvr} v^{2} r + Y_{vrr} vr^{2} \\ & N_{H} = N_{{\dot{v}}} \dot{v} + N_{{\dot{r}}} \dot{r} + N_{v} v + N_{vvv} v^{3} + N_{r} r + N_{rrr} r^{3} + N_{vvr} v^{2} r + N_{vrr} vr^{2} \\ \end{aligned} $$

(7)

4 Virtual Captive Model Test

The maneuvering characteristics of the high-speed catamaran are estimated by performing a virtual captive model test in order to get the hydrodynamic force. The computational conditions are depicted in Table 2.

Table 2. The computational conditions.

4.1 Static Drift Test

The ship travels through the tank in oblique flow due to a given drift angle $\beta$ in static drift test. The configuration in Fig. 3 and mathematical model Eq. (8) described static drift test:

$$ \begin{aligned} & X = X_{0} + X_{vv} v^{2} \\ & Y = Y_{0} + Y_{v} v + Y_{vvv} v^{3} \\ & N = N_{0} + N_{v} v + N_{vvv} v^{3} \\ \end{aligned} $$

(8)

Fig. 3.

Configuration of static drift test

4.2 Harmonic Test

The harmonic test includes pure sway, pure yaw, and combined yaw with drift test.

Pure sway test, the ship moves through the tank on straight-ahead course while it is oscillated from side to side. The pure sway motion expresses in terms of the velocities $u = {\text{constant}}$ while $r = 0$ and $v$ oscillates harmonically. The linear acceleration coefficients such as $Y_{{\dot{v}}}$ and $N_{{\dot{v}}}$ will be estimated in this test. The configuration in Fig. 4 and hydrodynamic forces in Eq. (9) determined for pure sway motion:

$$ \begin{aligned} & X = X_{0} + X_{vv} v^{2} \\ & Y = Y_{0} + Y_{{\dot{v}}} \dot{v} + Y_{v} v + Y_{vvv} v^{3} \\ & N = N_{0} + N_{{\dot{v}}} \dot{v} + N_{v} v + N_{vvv} v^{3} \\ \end{aligned} $$

(9)

Fig. 4.

Configuration of pure sway test

In harmonic motion, the Frourier series method (Sakamoto et al. 2012) is ultilized to simplify the mathematical models Eq. (9). Since hamonic motion are prescribed by sine and cosine function, hence hydrodynamic forces can be rewritten as Fourier series with angular frequency $\omega$:

$$ f = f_{0} + \sum\limits_{n = 1}^{3} {f_{cn} \cos (n\omega t) + \sum\limits_{n = 1}^{3} {f_{sn} \sin (n\omega t)} } $$

(10)

On the other hand, the harmonic forms are determined by replacing the motion equation ($v = - v_{\max } \cos \omega t$, $\dot{v} = \dot{v}_{\max } \sin \omega t$) into Eq. (9).

$$ \begin{aligned} & X = X_{0} + X_{c2} \cos 2\omega t \\ & Y = Y_{c1} \cos \omega t + Y_{s1} \sin \omega t + Y_{c3} \cos 3\omega \\ & N = N_{c1} \cos \omega t + N_{s1} \sin \omega t + N_{c3} \cos 3\omega \\ \end{aligned} $$

(11)

Pure yaw test, the ship moves through the tank while it conducts a pure yaw motion, where it is forced to follow the tangent of the oscillating path. The term of velocities is expressed that $v = 0$, while $r$ and $u$ oscillate harmonically. The hydrodynamic coefficients as $X_{rr}$, $Y_{{\dot{r}}}$, $Y_{r}$, $Y_{rrr}$, $N_{{\dot{r}}}$, $N_{r}$, and $N_{rrr}$ are estimated in the test. The configuration Fig. 5 and hydrodynamic forces in Eq. (12) defined for pure yaw motion:

$$ \begin{aligned} & X = X_{0} + X_{rr} r^{2} \\ & Y = Y_{0} + Y_{{\dot{r}}} \dot{r} + Y_{r} r + Y_{rrr} r^{3} \\ & N = N_{0} + N_{{\dot{r}}} \dot{r} + N_{r} r + N_{rrr} r^{3} \\ \end{aligned} $$

(12)

Fig. 5.

Configuration of pure yaw test

Combined yaw and drift is described the same as with pure yaw test, however, a drift angle is set on the motion in order to obtain a drift angle relative to the tangent of the oscillating path. The terms of velocity represents $v \ne 0$ and constant, while $r$ and $u$ oscillate harmonically. The coupling hydrodynamic coefficients as $X_{vr}$, $Y_{vvr}$, $Y_{vrr}$, $N_{vvr}$, and $N_{vrr}$ are estimated in this test. The combined pure yaw with drift test is described in Fig. 6 and hydrodynamic forces are shown in the below equation:

$$ \begin{aligned} & X = X_{0} + X_{vv} v^{2} + X_{rr} r^{2} + X_{vr} vr \\ & Y = Y_{0} + Y_{v} v + Y_{vvv} v^{3} + Y_{r} r + Y_{rrr} r^{3} + Y_{vvr} v^{2} r + Y_{vrr} vr^{2} \\ & N = N_{0} + N_{v} v + N_{vvv} v^{3} + N_{r} r + N_{rrr} r^{3} + N_{vvr} v^{2} r + N_{vrr} vr^{2} \\ \end{aligned} $$

(13)

Fig. 6.

Configuration of combined yaw and drift

Corresponding to pure sway test, the harmonic forms of pure yaw and combined yaw and drift are obtained by substituting motion equation ($r = r_{\max } \sin \omega t$, $\dot{r} = \dot{r}_{\max } \cos \omega t$) into Eqs. (12) and (13). Finally, coefficient of hamonic test can obtain from Fourier seriers as shown in Table 3.

Table 3. Fourier coefficients for harmonic test

The obtained hydrodynamic forces are non-dimensionalized by ship speed, ship length and water density as follows,

$$ \begin{aligned} & u^{\prime} = \frac{u}{U}; \, v^{\prime} = \frac{v}{U}; \, r^{\prime} = \frac{rL}{U} \\ & X^{\prime} = \frac{X}{{0.5\rho U^{2} L^{2} }}; \, Y^{\prime} = \frac{Y}{{0.5\rho U^{2} L^{2} }}; \, N^{\prime} = \frac{N}{{0.5\rho U^{2} L^{3} }} \\ \end{aligned} $$

(14)

5 Numerical Modeling

In order to simulate the virtual captive model tests, the CFD software ANSYS Fluent 2020R1 is applied. Incompressible unsteady RANS with $k - \omega$ SST turbulence model is used for simulating two-phase volume of the fluid technique. The volume of fluid (VOF) method is applied to capture the position of the free surface. In addition, a SIMPLE algorithm solves for pressure-velocity coupling. The y + value of 30 is estimated for Reynolds number of 7.3E+6.

The catamaran is covered by a rectangular domain to simulate the captive model test. According to Practical Guidelines for ship CFD Application (ITTC 2011) the dimensions of the domain are chosen to be able to avoid backflow and side flow. Additionally, boundary conditions are needed to assign for ensuring the physical characteristics of a fluid problem. The wall boundary condition represents the object’s surface, it is so-called no-slip wall. Pressure-inlet with open channel flow is required to start the calculation. Pressure-outlet with open channel flow is usually treated as a far-field condition, where flow properties are almost unchanged and hydrostatic pressure is specified. The symmetry condition indicates that the normal velocity and gradients of all variables at the symmetry plane is zero. The mesh generation for calculation is shown in Fig. 7.

Fig. 7.

Mesh generation

6 Results and Discustions

6.1 Validation

First at all, in order to estimate well the calculation of catamaran, a validation of the numerical method is conducted by comparing the results of CFD simulation with experimental results performed by Broglia et al. (2014). Resistance performance is simulated with a range of Froude numbers from 0.1–0.8. The comparison of the results in Figs. 8, 9, 10 and 11 shown the consistency between CFD and the experiment. Consequently, the CFD numerical method is appropriate to simulate the captive model tests.

Fig. 8.

The total resistance

Fig. 9.

The resistance coefficient

Fig. 10.

The sinkage

Fig. 11.

The trim

6.2 Hydrodynamic Forces

After validation the virtual captive model test is performed. The Froude number of 0.45 is selected for simulating high-speed catamaran. The reason for this selection due to fast increasing resistance and trim angle at this point as illustrated in Figs. 8, 9, 10 and 11. Moreover, sinkage is largest at Froude number 0.45 in Fig. 10.

The below figures show the results of hydrodynamic forces acting on catamaran for all the computed cases, which cover static drift, pure sway, pure yaw, and combined pure yaw with drift tests.

Fig. 12.

Hydrodynamic forces of static drift test

Fig. 13.

Fitting in-phase values of hydrodynamic forces versus lateral acceleration in pure sway test

Fig. 14.

Fitting in-phase values of hydrodynamic forces versus yaw rate in pure yaw test

Fig. 15.

Fitting out-phase values of hydrodynamic forces versus yaw rate in pure yaw test

Fig. 16.

Fitting out-phase values of hydrodynamic forces versus yaw rate in combined yaw with drift test

Fig. 17.

Wave pattern at various drift angle

The catamaran is symmetrical about the vertical center plane, the hydrodynamic forces acting on the hull in case of static drift are symmetrical in both positive and negative drift angles as shown in Fig. 12. The hydrodynamic forces in the case of harmonic motion are analyzed using the Fourier series. The added mass coefficients are obtained from in-phase values and damping coefficients are obtained from outphase values. On the other hand, the coupling coefficients are determined from the combined yaw with drift by subtracting forces acting on the hull in the single motions from the force acting on the hull in the combined motions. The obtained hydrodynamic forces are approximated using least square regression for each mathematical model in order to get hydrodynamic coefficients. Figures 13, 14, 15, 16 describe the hydrodynamic forces acting on the catamaran and fitting curves in the harmonic motion. It can be seen that the linear reactions are fitting very well to the hydrodynamic forces. The wave pattern of static drift test in Fig. 17 illustrates cause asymmetry wave pattern around the ship which leads to sway force and yaw moment and as drift angle increases the asymmetry of the wave pattern is clearly observed. Finally, the hydrodynamic coefficients obtained from CFD simulation in this study are listed in Table 4.

Table 4. Hydrodynamic coefficients.

7 Conclusions

In this paper, the CFD numerical method has been utilized for simulating the virtual captive model test of Delft 372 catamaran at the high-speed conditions. The straight and oblique motion was simulated in the stationary reference frame. The harmonic motions were implemented in the dynamic mesh motion using a user-defined function written by c programming.

The resistance performance was conducted to validate the CFD numerical method, an agreement was observed between the CFD method and experiment results. Additionally, the fitting resistance result using the least square method was found in first-order, second-order, and third-order terms.

Harmonic motions were performed for obtaining the added mass coefficient in pure sway and pure yaw test. Especially, the coupling coefficients were estimated in combined yaw with drift test. The Fourier series was applied for predicting the hydrodynamic coefficients in the harmonic test. The linear fitting using the least square method was observed very well to the hydrodynamic forces in the harmonic test.

The estimated coefficients will be used for predicting maneuvering characteristics in further study.