Keywords

1 Introduction

A multi-agent system is a collection of multiple autonomous, interacting agent, which is an important branch of distributed artificial intelligence. Such problems are significantly more difficult than those of single agent [1].

Reinforcement learning (RL) search for the optimal policy in a Markov process by obtaining as many rewards as possible. Articles [2] extends the Tit-for-tat policy with deep Q learning to maintain two agent cooperation even in the face of a prisoner's dilemma in order to achieve an optimal policy. Articles [3] investigates the performance of deep reinforcement learning. It is ultimately shown that deep reinforcement learning can achieve high performance. Articles [4] investigates the problem of cooperation in simple scenarios in a discrete structure for each agent that learns independently using the Q learning algorithm. The problem sizes studied above are typically a few agents, however, in real life, a large number of agents are indeed required to interact strategically with each other, such as fleet dispatch management problems [5], online role-playing games [6] or online advertising bidding auctions [7]. Existing multi-agent reinforcement learning solutions are effective, but they can only solve the problems of small-sized agent. In an environment where “an infinite number of agents are approached and imprecise probabilistic models are assumed to operate”, existing methods for deep reinforcement learning are not realistic [8]. Articles [9] designed an actor-critic algorithm to train a very large-scale taxi dispatching problem regionally. Articles [10] uses a centralized approach to learn distributed execution, learning to consider the Q-value function simultaneously. The team’s Q-value functions are decomposed into sums of their respective Q-value functions through a value decomposition network. Articles [11] uses a mixing network to combine local values, but this network is very difficult to train.

Learning between agents promotes each other: the learning of a single agent is based on the state of cluster agents [12].This paper proposes a multi-agent reinforcement learning algorithm based on a weighted mean field, using the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [13] as the framework in order to highlight the importance of different agents, the algorithm Based on related attribute sets, different weights are assigned to each agent action, and the weighted mean field is used to simplify the interactive information, which improves the performance of multi-agent reinforcement learning algorithms under large-scale multi-agents.

2 Weighted Mean Field Reinforcement Learning

2.1 Mean Field Theory

The mean field theory is a method of collectively processing the effects of the environment on individuals, and replacing the accumulation of multiple effects with mean effects. The strategic decision-making relationship between individuals and the whole and the relationship between joint strategy \(\pi \left( {s,a} \right)\) and single agent strategy \(\pi \left( {s,a_{i} } \right)\) in a multi-agent system.

Fig. 1.
figure 1

Evacuation diagram

Full size image

For example, many people do not know all the information about the surrounding environment, such as exit locations and routes, when people need to be evacuated urgently in Fig. 1. Each person does not need to observe the evacuation status of all people, but only needs to observe the status of the people around him. Based on the evacuation of the surrounding people, he can follow the people to different exits.

Wang [15] proposed the concept of mean field reinforcement learning (MFRL), but the use of mean field is simply to mean the action states of the surrounding agents of each agent and then import the critic network. But according to the multi-agent system consistency idea, the state information of different agents has different reference value to the central agent. Since exit 4 has the most people and may have the greatest impact on the evacuees, evacuees are directed to exit 4, in fact exit 2 is the best select. At this time, the surrounding people have different weights due to distance and other attributes. Those who are closer to the evacuees have a higher weight, and the evacuees are guided to choose the exit 2 which may be smaller but closer. At this time, the different distance or intimacy between each person forms a weight, and the relationship with the evacuees and the closest person. The weight distribution of the mean field is carried out through the influence of related factors, when applied to multi-agent reinforcement learning, it can better reflect the cluster effect of the mean field idea.

2.2 Weighted Mean Field

The size of the joint action increases exponentially with the size of the agent. All agents take their own strategy actions dynamically, which makes the reward function \(Q\left( {s,a} \right)\) unable to converge effectively. In order to solve this problem, the reward function is reconstructed, and the local joint action using weighted mean field is used as the parameter added value function.

$$ Q_{\mu }^{i} \left( {s,a} \right) = \frac{1}{{\omega \left( {x_{i} } \right)}}\sum\nolimits_{j \in N\left( i \right)} {\omega \left( {x_{i}^{j} } \right)Q^{i} \left( {s,a_{i} ,a_{j} } \right)} $$
(1)

Where \(N\left( i \right)\) is the collection of agents around the agent i, \(N^{i} = \left| {N\left( i \right)} \right|\) represents the number of agents around the agent i, \(\omega \left( {x_{i} } \right) = \mathop \sum \limits_{j \in N\left( i \right)} \omega \left( {x_{i}^{j} } \right)\), and \(\omega \left( {x_{i}^{j} } \right)\) is the weight coefficient function of the corresponding central agent i to the agent j. The weight parameters \(x_{i}^{j} = f\left( {Parameter 1, Parameter 2, \cdots } \right)\) are determined by the relevant agent attribute set, such as position, importance, intimacy, etc., which can be flexibly defined according to the scene and reward.

$$ \begin{aligned} Q_{\mu }^{i} \left( {s,a} \right) & = \frac{1}{{\omega \left( {x_{i} } \right)}}\mathop \sum \limits_{j} \omega \left( {x_{i}^{j} } \right)Q_{\mu }^{i} \left( {s,a_{i} ,a_{j} } \right) \\ & = \,\frac{1}{{\omega \left( {x_{i} } \right)}}\sum\nolimits_{j} {\omega \left( {x_{i}^{j} } \right)\left[ {Q_{\mu }^{i} \left( {s,a_{i} ,\overline{a}_{i} } \right)} \right.} + \nabla_{{\overline{a}_{i} }} Q_{\mu }^{i} \left( {s,a_{i} ,\overline{a}_{i} } \right){*}\updelta \alpha_{i,j} \\ & \, + \frac{1}{2}\delta \alpha_{i,j} *\nabla_{{\tilde{a}_{i,j} }}^{2} Q_{\mu }^{i} s,a_{i} ,\overline{a}_{i} {*}\updelta \alpha_{i,j} ] \\ & = \,Q_{\mu }^{i} \left( {s,a_{i} ,\overline{a}_{i} } \right) + \nabla_{{\overline{a} \overline{a}_{i} }} Q_{\mu }^{i} \left( {s,a_{i} ,\overline{a}_{i} } \right)*\left[ {\frac{1}{{\omega \left( {x_{i} } \right)}}\sum\nolimits_{j} {\delta \omega \left( {x_{i}^{j} } \right)\alpha_{i,j} } } \right] \\ & + \,\frac{1}{{2\omega \left( {x_{i} } \right)}}\sum\nolimits_{j} {\left[ {\delta \omega \left( {x_{i}^{j} } \right)\alpha_{i,j} *\nabla_{{\tilde{a}_{i,j} }}^{2} Q_{\mu }^{i} s,a_{i} ,\overline{a}_{i} {*}\updelta \alpha_{i,j} } \right]} \\ & \approx \,Q_{\mu }^{i} \left( {s,a_{i} ,a_{j} } \right) \\ \end{aligned} $$
(2)

For the \(Q_{\mu }^{i} \left( {s,a_{i} ,a_{j} } \right)\) according to Eq. (1), we approximate it by mean field theory, and the agent i action adopts \(a_{i}\). For example, Eq. (2) is used to calculate the mean weighted actions \(\overline{a}_{i}\) of the agents around the agent i, and the actions \(a_{j}\) of the neighboring agent j are converted into \(\overline{a}_{i}\) and a margin \(\delta \alpha_{i,j}\).

$$ \left\{ {\begin{array}{*{20}l} {\overline{a}_{i} = \frac{1}{{\omega \left( {x_{i} } \right)}}\sum\nolimits_{j} {\omega \left( {x_{i}^{j} } \right)a_{j} } } \hfill \\ {a_{j} = \overline{a}_{i} + \delta \alpha_{i,j} } \hfill \\ \end{array} } \right.,\,\,j \in N\left( i \right) $$
(3)

2.3 Weighted Mean Field Multi-agent Deep Deterministic Policy Gradient (WMPG)

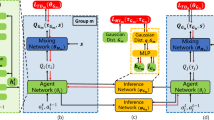
The decision-making behavior between multiple agents is transformed into the weighted behavior of central agent and adjacent agent by mean field theory, so as to modify the reward function and state value function of Multi-Agent Reinforcement Learning (MARL). By means of mean field theory, for example, the original critic network of multi-agent depth deterministic strategy gradient algorithm is simplified to the weighted mean of adjacent agent actions, which simplifies the calculation of other agent information, so that it can be applied to large-scale agent scenarios, and introduces weight information. The algorithm framework is shown in Fig. 2.

When calculating the loss function L and the strategy gradient, where \(Q_{\varphi }^{i} \left( {s,a_{1} , \cdots ,a_{n} } \right)\) is approximately transformed into \(Q_{\varphi }^{i} \left( {s,a_{i} ,\overline{a}_{i} } \right)\). The calculation of \(\overline{a}_{i}\) is as shown in Eq. (3), which simplifies the iteration of value function and state value function in critic network.

Fig. 2.
figure 2

Weighted Mean Field Multi-Agent Deep Deterministic Policy Gradient, WMPG

Full size image

The update mode of the critic network is changed to, \(\varphi\) is the weight parameter of the critic network

$$ L\left( {\varphi_{i} } \right) = \frac{1}{S}\sum\nolimits_{j} {\left( {y_{j} - Q_{{\varphi_{j} }}^{j} \left( {s,a_{j} ,\overline{a}_{j} } \right)} \right)^{2} } $$
(4)

Where \(S\) is the number of training samples \(\theta\) is actor network parameter, the gradient equation of actor network strategy can be written.

$$ \nabla_{{\theta_{j} }} J\left( {\theta_{i} } \right) \approx \left. {\frac{1}{S}\sum\nolimits_{j} {\nabla \theta_{j} \log \pi_{{\theta_{j} }}^{j} \left( s \right)} Q_{{\varphi_{j} }}^{j} \left( {s,a_{j} ,\overline{a}_{j} } \right)} \right|_{{a_{j} = \pi_{{\theta_{j} }} \left( s \right)}} $$
(5)

3 Experiment Results and Analysis

In order to verify the effectiveness of the algorithm, the performance of weighted mean field in large-scale Multi-Agent Reinforcement Learning is explored by using the Battle environment. Battle is a mixed combat multi-agent combat scenario of the open-source MAgent [16] framework. In Fig. 3, the blue side is the algorithm of this paper, and the red side is MFAC. It can be seen from the course of the battle that when an agent chooses to encircle, the nearby agents will be affected by the decision of the agent, thus forming a trend of encircling the red side by the blue side.

Fig. 3.
figure 3

Confrontation graph between WMPG and MFAC under Battle (Color figure online)

Full size image

3.1 Convergence Experiment

In order to show the training performance of the algorithm under different scale agents, this paper conducts experiments on the algorithm convergence of MADDPG which only uses mean field and weighted mean field. It can be seen that in a large scale, the convergence speed of this algorithm is obviously better than the other two. The multi-agent depth deterministic strategy gradient algorithm has been difficult to converge at the scale of 400. The weighted mean field algorithm proposed in this paper can reduce the difficulty of convergence to a certain extent (Fig. 4).

Fig. 4.
figure 4

Analysis of algorithm convergence under different agent scale

Full size image

3.2 Cross-Contrast

In order to prevent contingency, in the Battle environment, set the size of both agents to 200vs200.WMPG performed 200 rounds of cross-comparison with traditional reinforcement learning algorithm actor-critic AC, multi-agent deep reinforcement learning algorithm MADDPG, and mean field algorithm MFQ and MFAC [15] algorithm to verify the performance of this algorithm. Table 1 and Table 2 show the experimental results of the win rate and total return in the comparative experiment. It can be seen from the results in Table 1 that the WMPG algorithm is significantly better than other algorithms when experimenting with different types of algorithms, and from Table 2, it can be seen that the total return can also be higher, which also reflects the effectiveness of our algorithm. The poor performance of the multi-agent deep deterministic strategy gradient algorithm and the actor-critic algorithm also reflects the current traditional deep reinforcement learning algorithms mentioned in this article facing the problems of large-scale multi-agent systems. The research value of this article.

Table 1. The win rate of different algorithms
Full size table
Table 2. The total reward of different algorithms
Full size table

4 Conclusion

Based on the idea of mean field, this paper proposes a deep reinforcement learning algorithm of mean field multi-agent with weight information. Aiming at the problem that when the number of larger multi-agent systems exceeds a certain scale, the complex interactive information between agents will make the original reinforcement learning algorithm difficult to converge, and the weighted mean field is used to simplify the interactive information and transform the multi-agent information It is two-body information, used to simulate the interaction in the multi-agent system. The algorithm in this paper reduces the instability and difficulty of convergence of the combat environment in the open-source MAgent framework. In addition to giving certain proofs in theory, the experimental results also verify the rationality and effectiveness of this algorithm. In the follow-up, we need to consider the combination of large-scale multi-agent and mean field in heterogeneous scenarios.