Two-Dimensional Analytical Expression of Threshold Voltage for Un-doped Double Gate MOSFET

Abstract

In this work, new two-dimensional (2-D) analytical solution of threshold voltage (V_th) for un-doped Double Gate MOSFETs is proposed. In this research work, Green’s function based techniques are applied to solve the Poisson equations in 2-dimensional and we derived the threshold voltage (V_th) expression by using the concept of surface potential. This design is supposed uniform doping profile in Si area. The design is compared with existing experimental results and we got better solutions compared to existing works.

1 Introduction

In last two decades, VLSI (very large-scale integration) Technology CMOS has been used as a fundamental building block for low power system designs. Double-Gate (DG) MOSFET is emerging as a latest research domain in VLSI because the scaling of these devices is possible to the minimum channel length L possible for provided process technology parameters [1]. The scaling of MOSFET at deep submicron level has shown new and serious challenges for the designing and fabrication of future integrated circuits. When the MOSFET dimensions are scaled down, both the supply voltage and the gate t_ox be scaled down. The short channel effects [2] are controlled by scaling down both the gate-oxide thickness and channel length. The scaling of gate-oxide thickness is limited to about 1 nm because of high gate tunneling current [3, 4]. Scaling down the device dimension in nanometer regime, leakage currents plays an important role which needs more attention from the designer. Scalability of DG-MOSFETs is limited by sub-threshold swing which is an important design parameter. Formation of two channels in the symmetric DG MOSFET [5] provides steep sub-threshold swing, high drive current, and trans-conductance. The sub-threshold swing and other short channel effects can be optimized by using appropriate gate dielectric [6]. Therefore new MOSFET structures such as Dual Gate and Tri-Gate MOS transistors [7] are proposed to replace conventional planer MOSFET. It is also important that these new structure of MOSFETs are compatible with latest designing and fabrication techniques [8] of silicon integrated circuits. Dual gate MOSFETs also referred to as inversion charge transistors have many advantages over conventional MOSFETs. First, there is a considerable reduction in the device area. Second, DG MOSFET’s miller capacitance and output conductance can be further considerably reduced which makes it useful device for the designing of analog integrated circuits. Third, the breakdown voltage of the device can be made very high by using proper design methodology. Fourth, short channel effects in scaled devices are drastically minimized. Comparable to conventional MOSFET, in case of Dual Gate MOSFET, both gates control the properties of channel. Thus more scaling of gate length can be performed in DG MOSFETs. DG MOSFETs is better alternative of conventional MOSFETs because DG MOSFETs have improved on short channel effects. Also DG MOSFET has higher current density. Therefore performance of the devices can be maintained low leakage and higher current density by employing DG MOSFETs. In DG MOSFETs better manage short channel effects and V_th is achieved ideally without altering the concentration of channel dopants. This technique diminished the statistical dopant fluctuations [9] an also reduces the phenomena of impurity scattering. Many structures and techniques were used SOI devices with less short channel effects [10, 11]. Using DG MOSFETs can minimize short channel effects. The conventional MOSFET cannot be scaled down below 10 nm process technology. Therefore DG MOSFETs are widely employed in the analog electronic circuits where reduced short-channel effects, electronic gain control capability, high breakdown voltages are required. DG MOSFETs are fabricated in below 20 nm fabrication process technology by using metal gate technology for both the gates that diminished the poly depletion effects. The effects are degradation [12] and mobility of dopant atoms are eliminated of DG MOSFETs. Due to these advantages, an analytic and simple threshold-voltage model is highly desirable for un-doped DG MOSFETs as one of the key point parameters for the design of such nano-scale devices. More advantages of Dual Gate MOSFETs are improved trans-conductance, early voltage, and carrier transport efficiency. Accurate and physics-based formulations are required for implementation of high-speed VLSI circuits comprising of compact MOSFET model. Due to these requirements for the device, the un-doped symmetric DG MOSFETs are best-suited device structure because of the thin and un-doped nature of the channel. In the situation of surface inversion near oxide-silicon interface, the energy band bends up to 2Ф_B at the silicon-oxide interface. The same phenomena can be utilized for the analysis of the uniformly doped carrier concentration in the substrate. For the analytical modeling of the 2-D characteristics of DG MOSFETs, the two-dimensional Poisson’s equations are analyzed by using suitable initial and final boundary conditions. Concept of Green’s function techniques are used to get the solution for the two-dimensional Poisson’s equation considering the uniform doping profile. The modeling of DG MOSFET’s reported by authors [13,14,15,16,17,18,19]. For the optimization of the performance of the devices in nanometer regime for low power applications, V_th of the DG MOSFETs should be properly modeled. The analytical expression for 2-Dimensional V_th in the substrate is derived explicitly and verified by previous existing 2-Dimensional analytical models.

2 Structure of DG MOSFET

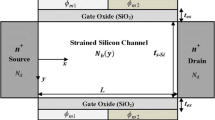
Figure 1 discusses the general structure of DG MOSFETs. In this structure of DG MOSFET 2 gates are used. Coupling is enhanced between gate to channel and hence short channel effects are considerably suppressed. DG MOSFETs are categorized as either symmetric DG MOSFET or asymmetric depends upon the voltages are applied to both gates. These two metal gates may or may not have same work functions. In this research work, analysis is done for symmetric DG MOSFETs. The symmetric DG MOSFETs means work function is similar for both gates. The thickness of the gate oxide is equal with same bias voltage is applied. After application of V_ds, V_gs, and with constant Quasi-Fermi level is shown in Fig. 1.

Fig. 1

Structure of general DG-MOSFET

3 Modeling of DG-MOSFET

3.1 he Basic Analysis

The cross-sectional view of a thin-film Dual Gate MOS device for two-Dimensional analytical model is shown in Fig. 2. The simplified domains for the analytical solution for the 2D Poisson’s equations [20,21,22,23] along with the suitable boundary conditions are shown in Eq. (1). The below equation shows the 2D Poisson’s equation with respect to rectangular coordinate system.

Fig. 2

Cross section view of DG-MOSFET

$${\Delta }^{2}{\varnothing }\left({x, y}\right)=-\frac{\uprho \left({x, y}\right)}{{\upvarepsilon }_{si}}=\frac{{q}{N}_{A}f\left(y\right)}{{\upvarepsilon }_{si}} , 0 \le y\le {t}_{si} ,0 \le x\le L$$

where ${N}_{A}$ is substrate acceptor and $f(y)$ is doping profile in Si area. The 2-D Poisson’s equations are converted into 2-D Laplace equations in the back and front oxide regions.

$$\left. {\begin{array}{*{20}c} {\emptyset \left( {0, y} \right) = V_{bi} \left( y \right)} & {0 < y < t_{si} } \\ {\emptyset \left( {L,y} \right) = V_{bi} \left( y \right) + V_{ds} } & {0 < y < t_{si} } \\ {D_{sf} \left( {x,0} \right) =\, \in_{si} E_{y} \left( {x,0} \right) } & {0 < x < L} \\ {D_{sb} \left( {x,t_{si} } \right) =\, \in_{si} E_{y} \left( {x,t_{si} } \right) } & {0 < x < L} \\ \end{array} } \right\}$$

(1)

$$\begin{gathered} E_{y} \left( {x,0} \right) = \frac{{\partial \phi \left( {x , y} \right)}}{\partial y} = \frac{{C_{ox} }}{{\varepsilon_{si} }}\left[ {V_{gs} - V_{fb} - \phi_{s} - \frac{{Q_{0} }}{{C_{ox} }}} \right], \hfill \\ E_{y} \left( {x,t_{si} } \right) = \frac{{\partial \phi \left( {x , y} \right)}}{\partial y} = - \frac{{C_{ox} }}{{\varepsilon_{si} }}\left[ {V_{gs} - V_{fb} - \phi_{s} - \frac{{Q_{0} }}{{C_{ox} }}} \right] \hfill \\ \end{gathered}$$

(2)

The concept of Green’s function technique is utilized for solution of the 2-Dimensional Poisson’s potential distribution. Simplifying the Green’s function solution into Green’s theorem [16], this is shown below

$$\begin{aligned} \emptyset \left( {x,y} \right) & = {\iint }\frac{{\rho \left( {x^{\prime}, y^{\prime}} \right)}}{\varepsilon }G\left( {x,y; x^{\prime},y^{\prime}} \right){\text{d}}x^{\prime}{\text{d}}y^{\prime} \\ & + \smallint G\left( {x,y; x^{\prime},y^{\prime}} \right)\frac{\partial \phi }{{\partial n^{\prime}}}{\text{d}}s^{\prime} - \smallint \Phi \left( {x^{\prime}, y^{\prime}} \right)\frac{\partial G}{{\partial n^{\prime}}}{\text{d}}s^{\prime} \\ \end{aligned}$$

(3)

where $G({x, y}; {x}^{{{\prime}} },{y}^{^{\prime}})$ is the Green’s function satisfying ${ \Delta }^{2}G=-\delta (x-{x}^{^{\prime}}) \delta (y-{y}^{^{\prime}})$, ${n}^{^{\prime}}$ is the outward direction.

$$G_{x} \left( {x,y;x^{\prime},y^{\prime}} \right) = \frac{2}{L}\mathop \sum \limits_{n = 1}^{\infty } \frac{{\sin \left( {K_{n} x^{\prime}} \right)\sin \left( {K_{n} x} \right)\sinh \left( {K_{n} y} \right)\sinh K_{n} \left( {t_{si} - y^{\prime}} \right)}}{{K_{n} \sinh K_{n} t_{si} }}, y < y^{\prime}$$

(4)

$$G_{x} \left( {x,y;x^{\prime},y^{\prime}} \right) = \frac{2}{L}\mathop \sum \limits_{n = 1}^{\infty } \frac{{\sin \left( {K_{n} x^{\prime}} \right)\sin \left( {K_{n} x} \right)\sinh \left( {K_{n} y^{\prime}} \right)\sinh K_{n} \left( {t_{si} - y} \right)}}{{K_{n} \sinh K_{n} t_{si} }}, y > y^{\prime}$$

(5)

$$G_{y} \left( {x,y;x^{\prime},y^{\prime}} \right) = \frac{2}{{t_{si} }}\mathop \sum \limits_{m = 1}^{\infty } \frac{{\sin \left( {K_{m} y^{\prime}} \right)\sin \left( {K_{m} y} \right)\sinh \left( {K_{m} x} \right)\sinh K_{m} \left( {L - x^{\prime}} \right)}}{{K_{m} \sinh K_{m} L}},x < x^{\prime}$$

(6)

$$G_{y} \left( {x,y;x^{\prime},y^{\prime}} \right) = \frac{2}{{t_{si} }}\mathop \sum \limits_{m = 1}^{\infty } \frac{{\sin \left( {K_{m} y^{\prime}} \right)\sin \left( {K_{m} y} \right)\sinh \left( {K_{m} x^{\prime}} \right)\sinh K_{m} \left( {L - x} \right)}}{{K_{m} \sinh K_{m} L}},x > x^{\prime}$$

(7)

Equation (3) is expression for electrostatic potential distribution and $\rho \left({x}^{{{\prime}} }, {y}^{^{\prime}}\right)=-q{N}_{A}f({y}^{^{\prime}})$ defined as the charge density of Si region. Assuming uniform doped ($f\left({y}^{^{\prime}}\right)=1$). 2D potential equation is shown below.

$$\begin{aligned} \emptyset (x,y) & = \frac{{( - qN_{A} )}}{{(2\varepsilon_{si} )}}x(L - x) + V_{bi} + V_{ds} \frac{x}{L} \\ & \quad + \sum\limits_{n = 1}^{\infty } {\frac{{(\sin K_{n} x)}}{{\varepsilon_{si} k_{n} \sinh k_{n} t_{s} i}}} \left[ {D_{sf}^{m} \cosh k_{n} (t_{si} - y) - D_{sb}^{m} \cosh k_{n} y} \right] \\ \end{aligned}$$

(8)

where ${D}_{sf}^{m}$ and ${D}_{sb}^{m}$ is electric displacement of front & back gate. The ${\varnothing }\left({x, y}\right)$ have to satisfy the boundary conditions,

$$\left. {\frac{{\partial \phi \left( {x , y} \right)}}{\partial x}} \right|_{{y = 0^{ + } }} - \left. {\frac{{\partial \phi \left( {x , y} \right)}}{\partial x}} \right|_{{y = 0^{ - } }} = 0$$

(9)

$$\left. { - \varepsilon_{si} \frac{{\partial \phi \left( {x , y} \right)}}{\partial y}} \right|_{{y = 0^{ + } }} + \left. {\varepsilon_{ox} \frac{{\partial \phi \left( {x , y} \right)}}{\partial y}} \right|_{{y = 0^{ - } }} = 0$$

(10)

After solving Eqs. (9) and (10) and we can obtain

$$D_{sf}^{m} = \frac{{\varepsilon_{{ox\left[ {B.D\varepsilon_{si} k_{n} \sinh k_{n} t_{si} - C.\sin K_{n} x} \right]}} }}{{\left[ {B.\varepsilon_{si} \sinh k_{n} t_{si} + B.\varepsilon_{ox} \cosh k_{n} t_{si} - A.\varepsilon_{ox} } \right].\sin K_{n} x}}$$

(11)

where coefficients

$$\begin{aligned} A & = \frac{{\sin K_{n} x}}{{K_{n} }}\left\{ {\frac{1}{{\varepsilon_{ox} }} + \frac{1}{{\varepsilon_{si} \tanh k_{n} t_{si} }} - \frac{1}{{\varepsilon_{si} \sinh k_{n} t_{si} }}} \right\}, \\ B & = \frac{{\sin K_{n} x}}{{K_{n} }}\left\{ {\frac{1}{{\varepsilon_{si} \sinh k_{n} t_{si} }} - \frac{1}{{\varepsilon_{si} \tanh k_{n} t_{si} }} - \frac{{\tanh k_{n} t_{ox} }}{{\varepsilon_{ox} }}} \right\} \\ \end{aligned}$$

(12)

$$\begin{aligned} C & = \frac{{2\sin K_{m} t_{ox} }}{{t_{ox} K_{m} \sinh k_{m} L}}\left\{ {V_{bi} \sinh K_{m} \left( {L - x} \right) + \left( {V_{bi} + V_{ds} } \right)\sinh K_{m} x} \right\} \\ D & = \frac{{4\left( {V_{gs} - V_{fb} } \right)\sinh K_{n} x}}{{n\pi \cosh k_{n} t_{ox} }} + \frac{{qN_{A} }}{{2\varepsilon_{si} }}x\left( {L - x} \right) - V_{bi} - V_{ds} \frac{x}{L} \\ \end{aligned}$$

(13)

3.2 Threshold Voltage Model

The location of ${X}_{min}$ lies on Si surface

$$\left. {\frac{{\partial \Phi \left( {x, y} \right) }}{\partial x}} \right|_{{x = x_{\min } , y = 0, t_{si} }} = 0$$

(14)

From Eq. (9), the position of the minimum surface potential ${x}_{min}$ is

$$\begin{aligned} & \frac{{ \varepsilon_{ox} \cosh k_{n} t_{si} }}{E}\left\{ {\frac{{qN_{A} }}{{\varepsilon_{si} }}\frac{{x_{\min } \left( {L - x_{\min } } \right)K_{n} }}{{\tan K_{n} x_{\min } }} - \frac{{qN_{A} }}{{2\varepsilon_{si} }}x_{\min } \left( {L - 2x_{\min } } \right)} \right. \\ & \left. {\quad - \frac{{V_{ds} }}{L} - \frac{{2V_{ds} }}{L}\frac{{x_{\min } K_{n} }}{{\tan K_{n} x_{\min } }} - \frac{{2V_{bi} K_{n} }}{{\tan K_{n} x_{\min } }} + \frac{{4\left( {V_{gs} - V_{fb} } \right)}}{{L.\cosh k_{n} t_{ox} \tan K_{n} x_{\min } }}} \right\} \\ & \quad - \frac{{qN_{A} }}{{2\varepsilon_{si} }}x_{\min } \left( {L - 2x_{\min } } \right) + \frac{{V_{ds} }}{L} = 0 \\ \end{aligned}$$

(15)

the expression for minimum surface potential ${\phi }_{sf,{\min}}$ is simplified as from above Eq. (15)

$$\begin{aligned} & \Phi_{\min } \left( {x_{\min } ,0} \right) = \frac{{ - qN_{A} }}{{2\varepsilon_{si} }}x_{\min } \left( {L - x_{\min } } \right) + V_{bi} + V_{ds} \frac{{x_{\min } }}{L} \\ & \quad + \mathop \sum \limits_{n = 1}^{\infty } \frac{{\sin K_{n} x_{\min } }}{{\varepsilon_{si} k_{n} \sinh k_{n} t_{si} }}\left[ {D_{sf}^{m} \cosh k_{n} t_{si} - D_{sb}^{m} } \right] =\Phi_{s,\min } \\ \end{aligned}$$

(16)

The ${V}_{\mathrm{th}}$ for the DG-MOSFET is derived from [24]. The V_th in terms of surface potential is expressed by

$$\begin{aligned} V_{{{\text{th}}}} & = V_{fb} + \left\{ {2\Phi_{f} + \frac{{ - qN_{A} }}{{2\varepsilon_{si} }}x_{\min } \left( {L - x_{\min } } \right) - V_{bi} - V_{ds} \frac{{x_{\min } }}{L}} \right\} \\ & \quad \frac{{\left\{ {\sin K_{n} x_{\min } } \right\}^{ - 1} }}{{2G_{f} }} - \frac{P}{{2G_{f} }} \\ \end{aligned}$$

(17)

where

$$\begin{aligned} G_{f} & = \left[ {1 - \left( { - 1} \right)^{n} } \right]\frac{R}{{d_{0} }}\left[ {\frac{2}{{m\pi \cosh k_{n} t_{ox} }} + \mathop \sum \limits_{m = 1}^{\infty } \frac{t}{{\left( {m - .5} \right)\pi }}\left[ {\left( { - 1} \right)^{m} - \frac{1}{{\left( {m - .5} \right)\pi }}} \right] } \right], \\ R & = - \frac{{\varepsilon_{si} }}{{\varepsilon_{ox} }}\frac{{\tanh k_{n} t_{ox} }}{{\sinh k_{n} t_{si} }},t = \frac{4}{n\pi }\left[ {1 + \frac{{L^{2} \left( {m - .5} \right)^{2} }}{{t_{ox}^{2} n^{2} }}} \right] \\ \end{aligned}$$

(18)

$$\begin{aligned} d_{0} & = \frac{1}{{\left( {\sinh k_{n} t_{si} } \right)^{2} }} - \left\{ {\frac{{\varepsilon_{si} \tanh k_{n} t_{ox} }}{{\varepsilon_{ox} }} + \frac{1}{{\tanh k_{n} t_{si} }}} \right\}^{2} , \\ P & = \frac{1}{{d_{0} }}\left\{ {\left[ {1 - \left( { - 1} \right)^{n} } \right]\frac{{qN_{A} L^{2} }}{{2\varepsilon_{si} }} \frac{8R}{{\left( {n.\pi } \right)^{3} }} + T\left[V_{bi} \left( {1 - \left( { - 1} \right)^{n} } \right) + V_{ds} \left( { - 1} \right)^{n + 1} \right]} \right\} \\ \end{aligned}$$

(19)

$$T = \mathop \sum \limits_{m = 1}^{\infty } 2Rt\left( {\left( {m - .5} \right)\pi } \right)^{ - 2} - \frac{4R}{{n\pi }}$$

(20)

$$V_{{th,{\text{long }}}} = V_{fb} - \frac{P}{{2G_{f} }}$$

(21)

The threshold voltage roll-off $\Delta {V}_{\mathrm{th}}$ expression is the difference between the values of threshold voltage for short channel and long-channel devices given as

$$\Delta V_{{{\text{th}}}} = \left\{ {2\Phi_{f} + \frac{{ - qN_{A} }}{{2\varepsilon_{si} }}x_{\min } \left( {L - x_{\min } } \right) - V_{bi} - V_{ds} \frac{{x_{\min } }}{L}} \right\}\frac{{\left\{ {\sin K_{n} x_{\min } } \right\}^{ - 1} }}{{2G_{f} }}$$

(22)

4 Results and Discussion

Figures 3 and 4 shows the various levels of threshold voltage roll-off ${\Delta V}_{\mathrm{th}}$ in the substrate the length of the channel length for various values of Si film ${t}_{si}$= (1.5, 5, 10, and 25 nm) at Gate ${t}_{ox}=1\; \mathrm{nm}$ and ${t}_{ox}=1.5\; \mathrm{nm}$ at same V_ds = 0.05 V and ${N}_{a}={10}^{17} \;{\mathrm{cm}}^{-3}$ for proposed analytical model and Chen [24]. The V_th roll-off increases with increase in ${t}_{si}$. With the increase in silicon film thickness, the curves are shifted towards right side for constant V_ds = 0.05 V and constant gate ${t}_{ox}=1\; \mathrm{nm}$ and ${t}_{ox}=1.5 \; \mathrm{nm}$. The proposed model shows Threshold Voltage roll-off ${\Delta V}_{\mathrm{th}}$ is 5–7% greater than Chen design.

Fig. 3

Proposed design compared with Chen [24], ${t}_{ox}=1\; \mathrm{nm}$

Fig. 4

Proposed design compared with Chen [24], ${ t}_{ox}=1.5\; \mathrm{nm}$

Figure 5 shows the parametric analysis for threshold voltage roll-off for various drain bias voltages ${V}_{ds}$= (0.005, 1.0 V) and the parameters are ${t}_{ox}=1.5\; \mathrm{nm}$ and silicon film thickness ${t}_{si}=10\; \mathrm{nm}$. Figures 3, 4, and 5 shows the threshold voltage roll-off ${\Delta V}_{\mathrm{th}}$. The proposed model accurately predicts the device behavior compared with the existing works Liang [1] and Chen [24], with 3–5% more accurate.

Fig. 5

Proposed design compared with Liang [1], ${t}_{si}=10\; \mathrm{nm}$ and ${t}_{ox}=1.5\; \mathrm{nm}$

5 Conclusion

The two-dimensional Poisson’s equations have been analytically derived using the concept of Green’s function incorporating suitable initial and final boundary conditions in Silicon area. The accuracy of the proposed model in the substrate (Si-film) is analyzed and verified by existing models. This design is valid for uniform doping profile in Si area. Due to the symmetry of DG-MOSFETS, the distributions of analytic potential for both sides of the surfaces in the substrate are same. It is obvious from simulation results so as to iterative method can only be used to find the minimum surface potential. It can be easily analyzed that better results are produced between the proposed and Chen [24] design analysis for parametric analysis of device structure for various biasing. The proposed analytic voltage model can be applied as a basic concept for high-speed physical analysis of the short-channel effects. It will define the deep-sub micrometer optimized scaling rule for thin-film Silicon on Insulator based MOS transistor in ULSI Technology.