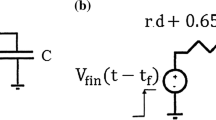Delay and Crosstalk Aware Analysis for High Speed On-Chip Global RLC VLSI Interconnects

Abstract

At the advanced stage of technologies, when feature size is being reduced, it is compulsory to introduce other parameters for more accurate modelling of transmission line interconnects. So mutual inductance and coupling capacitance how have become more important role for analysis of high-speed on-line VLSI interconnects. This paper introduces a mathematical aware analysis result for crosstalk noise of ‘L’ type RLC interconnections using mutual inductance. Two RLC interconnect lines of ‘L’ type, are equidistant to each other and used as ‘Aggressor line’ and ‘Victim line’ respectively, whereas, a step signal voltage is employed as input to aggressor line. Other calculative results for Delay and peak noise voltage between these two RLC electrical lines with using mutual inductance, are also introduced in this paper. This paper also shows a comparative result between our derived expression values and BKM values for simulation purpose.

1 Introduction

Presently, VLSI is the present level of designing and fabrication of ICs and microchips which consist of lacs of transistors on a single chip [1, 2]. In DSM region [3], now it is considered to study of inductive effect as well as capacitive-coupling effects to develop and explain the more accurate and real behaviour of on-chip VLSI interconnects. Delay and Crosstalk noise between VLSI high speed interconnected networks can have occurred due to self and mutual inductance. There are so many approaches presented [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] for the modelling of interconnect structures. This paper introduces use of closed loop of ‘L’ type RLC interconnect network. Two RLC parallel interconnects and a mutual inductance and coupling capacitance are occurred automatically. These two RLC networks are named as ‘aggressor line’ and ‘victim line’ respectively. The proposed work is much improved work of the BKM [19] model. This paper establishes a mathematical equation of crosstalk voltage of mutually inductively coupled interconnections of RLC type. This paper also introduces expressions for delay and peak noise voltage between adjacent RLC network. This paper is organized remaining follows: Sect. 2 describes Proposed models and of crosstalk voltage and delay analysis. Detailed results of simulation are discussed in portion 3 and portion 4 conclude the paper.

2 Proposed Model

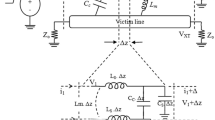
Mathematical and analytical expressions for the crosstalk voltage, delay and peak crosstalk voltage are derived in the case only when victim lines are grounded and excitation is connected to aggressor line. Figure 1 shows lumped RLC model of ‘L’ shaped interconnection system considering Mutual Inductance coupling between the parallel lines. Step input voltage is used for the analysis of the interconnection system.

Fig. 1

Equivalent Circuit of RLC interconnects using ‘L’ shaped interconnect model with effect of Mutual Inductance m

A step input voltage supply is given to the input of aggressor line which is equidistant to the victim lines. Coupling capacitance is generated because those two RLC networks are proximate to each other and mutual inductance is induced due to using inductor coil.in this paper we use 90 nm technology.

As per Moore’s law, in the process of designing the ICs, the number of transistors will continue to double in every 18 months [1]. That means the same silicon area would accommodate a greater number of transistors. Transistors size is gradually getting reduced for achieving this or we can say that transistor size is shifting from one technology node to smaller technology node by using scaling process. A specific technology gets used by the industries for the period of time till the time when the next feasible smaller technology node would be ready for implantation. For example, 180 nm technology was used mostly in 1999–2000-time period whereas 90 nm technology was used in 2004–2005. The technology’s numbers represent the minimum feature size of transistor or CMOS. Minimum channel length that can be used in fabrication of CMOS or transistor is known as Feature size of transistor. These numbers are decided by dividing the previous number (technology) by square root of two ($\sqrt{2}$).

In the circuit shown in Fig. 1, at node C, we develop the mathematical expression for the voltage for RLC victim line.

On employing KVL in 1^st loop:

$${V}_{S1}={I}_{1}{R}_{d1}+{I}_{1}{R}_{1}+{L}_{1}\frac{d{I}_{1}}{dt}-m\frac{d{I}_{3}}{dt}+\frac{1}{{C}_{2}}\int \left({I}_{1}-{I}_{2}\right)dt$$

(1)

On taking Laplace,

$${V}_{S1}\left(s\right)={I}_{1}\left(s\right){R}_{d1}+{I}_{1}\left(s\right){R}_{1}+{L}_{1}S{I}_{1}\left(s\right)-mS{I}_{3}\left(s\right)+\frac{1}{s{C}_{1}}\left[{I}_{1}\left(s\right)-{I}_{2}\left(s\right)\right]$$

(2)

$${V}_{S1}\left(s\right)=\frac{\left({M}_{1}S{C}_{1}\right){I}_{1}\left(s\right)-{I}_{2}\left(s\right)}{S{C}_{1}}-mS{I}_{3}\left(s\right)$$

(3)

Where,

$${M}_{1}={R}_{d1}+{R}_{1}+{L}_{1}S$$

(4)

Similarly, on applying KVL in 2^nd mesh,

$$\frac{1}{s{C}_{1}}\left[{I}_{1}\left(s\right)-{I}_{2}\left(s\right)\right]=\frac{1}{S{C}_{C1}}{I}_{2}\left(s\right)+\frac{1}{S{C}_{1}^{^{\prime}}}\left[{I}_{2}\left(s\right)+{I}_{3}\left(s\right)\right]$$

$$\frac{1}{s{C}_{1}}{I}_{1}\left(s\right)-\left[\frac{1}{s{C}_{1}}+\frac{1}{S{C}_{1}^{^{\prime}}}+\frac{1}{S{C}_{C1}}\right]{I}_{2}\left(s\right)-\frac{1}{S{C}_{1}^{^{\prime}}}{I}_{3}\left(s\right)=0$$

(5)

Similarly, on applying KVL in 3^rd mesh,

$$0={I}_{3}\left(s\right){R}_{d2}+{I}_{3}\left(s\right){R}_{1}^{^{\prime}}+S{L}_{1}^{^{\prime}}{I}_{3}\left(s\right)-Sm{I}_{1}\left(s\right)+\frac{1}{S{C}_{1}^{^{\prime}}}\left[{I}_{2}\left(s\right)+{I}_{3}\left(s\right)\right]$$

$${I}_{1}\left(s\right)\left[-{s}^{2}m{C}_{1}^{^{\prime}}\right]+{I}_{2}\left(s\right)+\left(S{M}_{2}{C}_{1}^{^{\prime}}+1\right)=0$$

(6)

Where

$${M}_{2}={R}_{d1}+{R}_{1}^{^{\prime}}+s{L}_{1}^{^{\prime}}$$

From Eqs. (3), (5) and (6), we get a matrix:

$$\left[\begin{array}{ccc}\frac{{M}_{1}S{C}_{1}+1}{S{C}_{1}}& -\frac{1}{s{C}_{1}}& -ms\\ \frac{1}{s{C}_{1}}& -\left[\frac{1}{s{C}_{1}}+\frac{1}{S{C}_{1}^{^{\prime}}}+\frac{1}{S{C}_{C1}}\right]& -\frac{1}{s{C}_{1}}\\ -{s}^{2}m{C}_{1}^{^{\prime}}& 1& (S{M}_{2}{C}_{1}^{^{\prime}}+1)\end{array}\right]\left[\begin{array}{c}{I}_{1}\left(s\right)\\ {I}_{2}\left(s\right)\\ {I}_{3}\left(s\right)\end{array}\right]=\left[\begin{array}{c}{V}_{s1}\left(s\right)\\ 0\\ 0\end{array}\right]$$

Let,

$${M}_{1}S{C}_{1}+1=A, B=-\left[\frac{1}{s{C}_{1}}+\frac{1}{S{C}_{1}^{^{\prime}}}+\frac{1}{S{C}_{C1}}\right],$$

$$\left(S{M}_{2}{C}_{1}^{^{\prime}}+1\right)=C$$

Then required matrix is,

$$\left[\begin{array}{ccc}\frac{A}{s{C}_{1}}& \frac{-1}{s{C}_{1}}& -mS\\ \frac{1}{s{C}_{1}}& -B& \frac{-1}{s{C}_{1}}\\ -{s}^{2}m{C}_{1}^{^{\prime}}& 1& C\end{array}\right]\left[\begin{array}{c}{I}_{1}\left(s\right)\\ {I}_{2}\left(s\right)\\ {I}_{3}\left(s\right)\end{array}\right]=\left[\begin{array}{c}{V}_{s1}\left(s\right)\\ 0\\ 0\end{array}\right]$$

After solving by Cramer’s rule [20],

$$I_{1} \left( s \right) = \frac{{sC_{1}^{2} \left[ {1 - CC_{1}^{^{\prime}} s} \right]V_{s1} }}{{ - sABCC_{1} C_{1}^{^{\prime}} - 2s^{2} mC_{1} C_{1}^{^{\prime}} + Bs^{5} m^{2} C_{1}^{2} C_{1}^{^{\prime}2} + AC_{1} + CC_{1} }}$$

(7)

$$I_{2} \left( s \right) = \frac{{sC_{1} C_{1}^{^{\prime}} \left[ {ms^{2} C_{1} - C} \right]V_{s1} }}{{ - sABCC_{1} C_{1}^{^{\prime}} - 2s^{2} mC_{1} C_{1}^{^{\prime}} + Bs^{5} m^{2} C_{1}^{2} C_{1}^{^{\prime}2} + AC_{1} + CC_{1} }}$$

(8)

$$I_{3} \left( s \right) = \frac{{sC_{1} C_{1}^{^{\prime}} \left[ {1 - 3s^{3} mC_{1} C_{1}^{^{\prime}} } \right]V_{s1} }}{{ - sABCC_{1} C_{1}^{^{\prime}} - 2s^{2} mC_{1} C_{1}^{^{\prime}} + Bs^{5} m^{2} C_{1}^{2} C_{1}^{^{\prime}2} + AC_{1} + CC_{1} }}$$

(9)

Now, at node ‘C’:

$${V}_{c}=\frac{1}{s{C}_{1}^{^{\prime}}}\left[{I}_{2}\left(s\right)+{I}_{3}\left(s\right)\right]$$

(10)

So,

$${{V}}_{{c}}=\frac{{{sC}}_{1}{{C}}_{1}^{{^{\prime}}}{{V}}_{{s}1}}{{{sC}}_{1}^{{^{\prime}}}}\left[\frac{{{ms}}^{2}{{C}}_{1}-{C}+1-{{Bs}}^{3}{{mC}}_{1}{{C}}_{1}^{{^{\prime}}}}{-{{sABCC}}_{1}{{C}}_{1}^{{^{\prime}}}-2{{s}}^{2}{{mC}}_{1}{{C}}_{1}^{{^{\prime}}}+{{Bs}}^{5}{{m}}^{2}{{C}}_{1}^{2}{{C}}_{1}^{{^{\prime}}2}+{{AC}}_{1}+{{CC}}_{1}}\right]$$

$${V}_{c}=\frac{{C}_{1}{V}_{s1}\left[m{s}^{2}{C}_{1}-C+1-B{s}^{3}m{C}_{1}{C}_{1}^{^{\prime}}\right]}{P}$$

(11)

Where,

$P = - sABCC_{1} C_{1}^{^{\prime}} - 2s^{2} mC_{1} C_{1}^{^{\prime}} + Bs^{5} m^{2} C_{1}^{2} C_{1}^{^{\prime}2} + AC_{1} + CC_{1}$ After substituting the values of A, B and C:

$$\begin{aligned} {\text{P}} = & - {\text{sC}}_{1} {\text{C}}_{1}^{^{\prime}} \left( {{\text{M}}_{1} {\text{sC}}_{1} + 1} \right)\left( {\frac{ \propto }{{{\text{sC}}_{1} {\text{C}}_{1}^{^{\prime}} {\text{C}}_{{{\text{C}}1}} }}} \right)\left( {{\text{sM}}_{2} {\text{C}}_{1}^{^{\prime}} + 1} \right) - 2{\text{s}}^{2} {\text{mC}}_{1} {\text{C}}_{1}^{^{\prime}} + \\ & \left( {\frac{ \propto }{{{\text{sC}}_{1} {\text{C}}_{1}^{^{\prime}} {\text{C}}_{{{\text{C}}1}} }}} \right){\text{s}}^{5} {\text{m}}^{2} {\text{C}}_{1}^{2} {\text{C}}_{1}^{{{^{\prime}}2}} + \left( {{\text{M}}_{1} {\text{sC}}_{1} + 1} \right){\text{C}}_{1} + \left( {{\text{sM}}_{2} {\text{C}}_{1}^{^{\prime}} + 1} \right){\text{C}}_{1}^{^{\prime}} \\ \end{aligned}$$

Where,

$$B=\frac{\propto }{s{{C}_{C1}C}_{1}{C}_{1}^{^{\prime}}}$$

Where,

$$\propto ={C}_{1}^{^{\prime}}{C}_{C1}+{{C}_{C1}C}_{1}+{C}_{1}{C}_{1}^{^{\prime}}$$

Now,

$$\begin{aligned} & {\text{P}} = - \propto \left( {M_{1} sC_{1} + 1} \right)\left( {sM_{2} C^{\prime}_{1} + 1} \right) - 2s^{2} mC_{1} C^{\prime}_{1} + \frac{ \propto }{{C^{\prime}_{1} }}s^{4} m^{2} C_{1} C^{\prime}_{1} \\ & \quad \;\;\, + \left( {M_{1} sC_{1} + 1} \right)C_{1} + \left( {sM_{2} C^{\prime}_{1} + 1} \right)C^{\prime}_{1} \\ \end{aligned}$$

After neglecting all high-power terms:

$$P={s}^{2}{C}_{1}{C}_{1}^{^{\prime}}\left[\propto {M}_{1}{M}_{2}+2m\right]+s\left[-\propto {M}_{1}{C}_{1}-\propto {M}_{1}{C}_{1}^{^{\prime}}+{M}_{1}{C}_{1}+{M}_{2}{C}_{1}^{^{\prime}}\right]+{C}_{1}+{C}_{1}^{^{\prime}}-\propto$$

(12)

Now after substituting the value of ${V}_{s1}=\frac{1}{s}$ (for step input voltage) & P in Eq. (11),

$${V}_{c}=\frac{{C}_{1}\left(sm{C}_{1}-{M}_{2}{C}_{1}^{^{\prime}}\right)}{{s}^{2}{C}_{1}{C}_{1}^{^{\prime}}\left[\propto {M}_{1}{M}_{2}+2m\right]+s\left[-\propto {M}_{1}{C}_{1}-\propto {M}_{1}{C}_{1}^{^{\prime}}+{M}_{1}{C}_{1}+{M}_{2}{C}_{1}^{^{\prime}}\right]+{C}_{1}^{^{\prime}}+{C}_{1}^{^{\prime}}-\propto }$$

Now, let us assume:

$$X={C}_{1}{C}_{1}^{^{\prime}}\left[\propto {M}_{1}{M}_{2}+2m\right]$$

$$Y=-\propto {M}_{1}{C}_{1}-\propto {M}_{1}{C}_{1}^{^{\prime}}+{M}_{1}{C}_{1}+{M}_{2}{C}_{1}^{^{\prime}}$$

$$Z={C}_{1}^{^{\prime}}+{C}_{1}^{^{\prime}}-\propto$$

$$P =-{X}^{2}s+Ys+Z$$

(13)

$${V}_{c}=\frac{{C}_{1}\left(sm{C}_{1}-{M}_{2}{C}_{1}^{^{\prime}}\right)}{{-Xs}^{2}+Ys+Z}$$

$${V}_{c}=\frac{-m{C}_{1}^{2}s}{{Xs}^{2}-Ys-Z}+\frac{{M}_{2}{C}_{1}^{^{\prime}}}{{Xs}^{2}-Ys-Z}$$

$$V_{c} = \frac{{{\raise0.7ex\hbox{${ - mC_{1}^{2} s}$} \!\mathord{\left/ {\vphantom {{ - mC_{1}^{2} s} X}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$X$}}}}{{s^{2} - \frac{Y}{X}s - \frac{Z}{X}}} + \frac{{{\raise0.7ex\hbox{${M_{2} C_{1}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{M_{2} C_{1}^{^{\prime}} } X}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$X$}}}}{{s^{2} - \frac{Y}{X}s - \frac{Z}{X}}}$$

$$V_{c} = \frac{{{\raise0.7ex\hbox{${ - mC_{1}^{2} s}$} \!\mathord{\left/ {\vphantom {{ - mC_{1}^{2} s} X}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$X$}}}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + \left[ {\sqrt {\frac{ - Z}{X} - \frac{{Y^{2} }}{{4X^{2} }}} } \right]^{2} }} + \frac{{{\raise0.7ex\hbox{${M_{2} C_{1}^{^{\prime}} }$} \!\mathord{\left/ {\vphantom {{M_{2} C_{1}^{^{\prime}} } X}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$X$}}}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + \left[ {\sqrt {\frac{ - Z}{X} - \frac{{Y^{2} }}{{4X^{2} }}} } \right]^{2} }}$$

If, $R={\left[\sqrt{\frac{-Z}{X}-\frac{{Y}^{2}}{4{X}^{2}}}\right]}^{2}$

After taking Inverse Laplace transform:

$${V}_{c}\left(t\right)=-\left[{e}^{\frac{Y}{2X}t}\mathrm{cos}\,Rt\right] \frac{m{C}_{1}^{2}}{X}+\left[{e}^{\frac{Y}{2X}t}\mathrm{sin}\,Rt\right]\frac{{M}_{2}{C}_{1}^{^{\prime}}}{X}$$

$${V}_{c}\left(t\right)=\frac{{e}^{\frac{Y}{2X}t}}{X}\left[{M}_{2}{C}_{1}^{^{\prime}}\mathrm{sin}\,Rt-m{C}_{1}^{2}\mathrm{cos}\,Rt\right]$$

(14)

Peak time value ${t}_{{p}_{c}}$ is calculated by equating first derivative of ${V}_{c}\left(t\right)$ to zero,

$$\frac{d{V}_{c}\left(t\right)}{dt}=0$$

$${M}_{2}{C}_{1}^{^{\prime}}\frac{d}{dt}\left[{e}^{\frac{Y}{2X}t}\mathrm{sin}\,Rt\right]- m{C}_{1}^{2}\frac{d}{dt}\left[{e}^{\frac{Y}{2X}t}\mathrm{cos}\,Rt\right]=0$$

After simplification we get

$${t}_{{p}_{c}}=t=\frac{1}{R}{\mathrm{tan}}^{-1}\left[\frac{-R{M}_{2}{C}_{1}^{^{\prime}}+\left(\frac{m{C}_{1}^{2}}{2}\right)\left(\frac{Y}{X}\right)}{Rm{C}_{1}^{2}+\left(\frac{{M}_{2}{C}_{1}^{^{\prime}}}{2}\right)\left(\frac{Y}{X}\right)}\right]$$

(15)

Let’s put the value t = ${t}_{{p}_{c}}$ in Eq. (14) so that,

$${V}_{c}\left(t\right)=\frac{{t}_{{c}_{(t)max}}}{{t}_{={t}_{{p}_{c}}}}$$

$${V}_{c}{\left(t\right)}_{max}={e}^{\frac{Y}{2X}{t}_{{p}_{c}}}\left[{M}_{2}{C}_{1}^{^{\prime}}\mathrm{sin}R{t}_{{p}_{c}}-m{C}_{1}^{2}\mathrm{cos}R{t}_{{p}_{c}}\right]$$

(16)

Now calculate the value of ${V}_{B}$:

$${V}_{B}=\frac{1}{s{C}_{1}}\left[{I}_{1}\left(s\right)-{I}_{2}\left(s\right)\right]$$

$$V_{B} = \frac{{V_{s1} }}{{sC_{1} }}\left[ {\frac{{sC_{1}^{2} \left[ {1 - BCC_{1}^{^{\prime}} s} \right] - sC_{1} C_{1}^{^{\prime}} \left[ {ms^{2} C_{1} - C} \right]}}{{ - sABCC_{1} C_{1}^{^{\prime}} - 2s^{2} mC_{1} C_{1}^{^{\prime}} + Bs^{5} m^{2} C_{1}^{2} C_{1}^{^{\prime}2} + AC_{1} + CC_{1} }}} \right]$$

For unit step input, ${V}_{s1}=\frac{1}{s}:$

$${V}_{B}=\frac{\frac{1}{s}\left[{C}_{1}-\frac{s\propto {C}_{1}{C}_{1}^{^{\prime}}}{s{C}_{1}{C}_{1}^{^{\prime}}{C}_{C1}}\left(1+s{M}_{2}{C}_{1}^{^{\prime}}\right)-m{C}_{1}{C}_{1}^{^{\prime}}{s}^{2}-{C}_{1}^{^{\prime}}\left(1+s{M}_{2}{C}_{1}^{^{\prime}}\right)\right]}{P}$$

$$V_{B} = \frac{{\frac{1}{s}\left[ {C_{1} - \frac{ \propto }{{C_{C1} }} - \frac{{sM_{2} C_{1}^{^{\prime}} }}{{C_{C1} }} - mC_{1} C_{1}^{^{\prime}} s^{2} - M_{2} s} \right]}}{P}$$

Now let’s put the value of P from expression (12) and have,

$$V_{B} = \frac{{C_{1} C_{C1} - \propto - s\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right) - mC_{1} C_{1}^{^{\prime}} C_{C1} s^{2} - C_{1}^{^{\prime}} C_{C1} }}{{C_{C1} s\left[ { - s^{2} C_{1} C_{1}^{^{\prime}} \left( { \propto M_{1} M_{2} + 2m} \right) + s\left( { - \propto M_{1} C_{1} - \propto M_{2} C_{1}^{^{\prime}} + M_{1} C_{1} + M_{2} C_{1}^{^{\prime}} } \right) + \left( {C_{1} + C_{1}^{^{\prime}} - \propto } \right)} \right]}}$$

$$V_{B} = \frac{{C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} }}{{sPC_{C1} }} - \frac{{msC_{1} C_{1}^{^{\prime}} C_{C1} }}{{PC_{C1} }} - \frac{{\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}}{{PC_{C1} }}$$

$${V}_{B}=\frac{{C}_{1}{C}_{C1}-\propto -{C}_{1}^{^{\prime}}{C}_{C1}/{C}_{C1}}{sP}-\frac{m{C}_{1}{C}_{1}^{^{\prime}}s}{P}-\frac{\left({M}_{2}{C}_{1}^{^{\prime}}+{M}_{2}{C}_{1}^{^{\prime}}{C}_{C1}\right)/{C}_{C1}}{P}$$

$${V}_{B}={V}_{B1}-{V}_{B2}-{V}_{B3}$$

(17)

Where,

$${V}_{B1}=\frac{{C}_{1}{C}_{C1}-\propto -{C}_{1}^{^{\prime}}{C}_{C1}/{C}_{C1}}{sP}$$

$${V}_{B2}=\frac{ms{C}_{1}{C}_{1}^{^{\prime}}}{P}$$

$${V}_{B3}=\frac{\left({M}_{2}{C}_{1}^{^{\prime}}+{M}_{2}{C}_{1}^{^{\prime}}{C}_{C1}\right)/{C}_{C1}}{P}$$

Putting the result of P in the equation of V_B1 from Eq. (13)

$$V_{B1} = \frac{{{\raise0.7ex\hbox{${C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} }$} \!\mathord{\left/ {\vphantom {{C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} } {C_{C1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${C_{C1} }$}}}}{{s\left( { - Xs^{2} + Ys + Z} \right)}}$$

after simplification, we get,

$${V}_{B1}=\frac{{C}_{1}{C}_{C1}-\propto -{C}_{1}^{^{\prime}}{C}_{C1}}{{C}_{C1}}\left[\frac{1}{Zs}-\frac{1}{Z\left(s+\frac{Z}{Y}\right)}\right]$$

In similar way, the expressions of V_B2 and V_B3 after substituting the expression of P from Eq. (13),

$$V_{B2} = \frac{{\frac{{ - mC_{1} C_{1}^{^{\prime}} }}{X}s}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + R^{2} }},\;\;\;V_{B3} = \frac{{{\raise0.7ex\hbox{${\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)} {XC_{C1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${XC_{C1} }$}}}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + R^{2} }}$$

Where,

$$R={\left[\sqrt{\frac{-Z}{X}-\frac{{Y}^{2}}{4{X}^{2}}}\right]}^{2}$$

substituting the values of ${V}_{B1},{V}_{B2},{V}_{B3}$ in Eq. (17)

$$\begin{array}{*{20}c} {V_{B} \left( s \right) = \frac{{C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} }}{{C_{C1} }}\left[ {\frac{1}{Z}\left( {\frac{1}{s} - \frac{1}{{\left( {s + \frac{Z}{Y}} \right)}}} \right)} \right]} \\ { + \frac{{\frac{{mC_{1} C_{1}^{^{\prime}} }}{X}s}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + R^{2} }} + \frac{{{\raise0.7ex\hbox{${\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)} {XC_{C1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${XC_{C1} }$}}}}{{\left[ {s - \frac{Y}{2X}} \right]^{2} + R^{2} }}} \\ \end{array}$$

After using inverse Laplace Transform in the above expression

$$\begin{array}{*{20}l} {V_{B} \left( t \right) = \frac{{\left( {C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} } \right)\left( {1 - e^{{ - \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z Y}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$Y$}}} \right)t}} } \right)}}{{C_{C1} Z}} + \left[ {e^{{\frac{Y}{2X}t}} \cos Rt} \right]\frac{{mC_{1} C_{1}^{^{\prime}} }}{X}} \hfill \\ { + \left[ {e^{{\frac{Y}{2X}t}} \sin Rt} \right]\frac{{\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right) }}{{C_{C1} X}}} \hfill \\ \end{array}$$

(18)

On differentiating with respect to t

$$\begin{array}{*{20}l} {\frac{{dV_{B} \left( t \right)}}{dt} = \frac{{\left( {C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} } \right)}}{{C_{C1} Y}}e^{{ - \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z Y}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$Y$}}} \right)t}} + \frac{{mC_{1} C_{1}^{^{\prime}} }}{X}\left[ {\frac{Y}{2X}e^{{\frac{Y}{2X}t}} \cos Rt + } \right.} \hfill \\ {\left. { \left( { - R\sin Rt} \right)e^{{\frac{Y}{2X}t}} } \right] + \frac{{\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}}{{C_{C1} X}}\left[ {\frac{Y}{2X}e^{{\frac{Y}{2X}t}} \sin Rt + R\cos Rte^{{\frac{Y}{2X}t}} } \right]} \hfill \\ \end{array}$$

Peak time value is calculated by equating first derivative to zero,

$$\begin{array}{*{20}l} {\frac{{\left( {C_{1} C_{C1} - \propto - C_{1}^{^{\prime}} C_{C1} } \right)}}{{C_{C1} Y}}e^{{ - \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z Y}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$Y$}}} \right)t_{p} }} + \cos Rt_{p} e^{{\frac{Y}{2X}t_{p} }} \left[ {\frac{Y}{{2X^{2} }}mC_{1} C_{1}^{^{\prime}} + \frac{{R\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}}{{C_{C1} X}}} \right] + } \hfill \\ {\sin Rt_{p} e^{{\frac{Y}{2X}t_{p} }} \left[ {\frac{Y}{{2X^{2} C_{C1} }}\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right) - \frac{R}{X}mC_{1} C_{1}^{^{\prime}} } \right] = 0} \hfill \\ \end{array}$$

Let us assume for simplicity,

$$q=\frac{\left({C}_{1}{C}_{C1}-\propto -{C}_{1}^{^{\prime}}{C}_{C1}\right)}{{C}_{C1}Y}$$

$$u = \frac{Y}{{2X^{2} }}mC_{1} C_{1}^{^{\prime}} + \frac{{R\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right)}}{{C_{C1} X}}$$

$$v = \frac{Y}{{2X^{2} C_{C1} }}\left( {M_{2} C_{1}^{^{\prime}} + M_{2} C_{1}^{^{\prime}2} C_{C1} } \right) - \frac{R}{X}mC_{1} C_{1}^{^{\prime}}$$

After simplification above equation becomes,

$$q.e^{{ - \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z Y}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$Y$}}} \right)t_{p} }} + \cos Rt_{p} e^{{\frac{Y}{2X}t_{p} }} .u + \sin Rt_{p} e^{{\frac{Y}{2X}t_{p} }} .v = 0$$

$$q.e^{{ - \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z Y}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$Y$}}} \right)t_{p} }} + e^{{\frac{Y}{2X}t_{p} }} \left( {u.\cos Rt_{p} + v.\sin Rt_{p} } \right) = 0$$

(19)

After simplification and approximation to lower degree terms of above Eq. (19), we get

$${t}_{p}=\frac{2XY\left(u+q\right)}{qZ-2XYvR-u{Y}^{2}}$$

(20)

$${t}_{p}=\frac{H}{I}$$

where,

$$H=2XY\left(u+q\right), I= qZ-2XYvR-u{Y}^{2}$$

After substituting the values of ${t}_{p}$ in equation, so now

$$\begin{array}{*{20}l} {{{V}}_{{{{Bmax}}}} \left( {{t}} \right) = \left( {\frac{{{{C}}_{1} {{C}}_{{{{C}}1}} - \propto - {{C^{\prime}}}_{{{1}}} {{C}}_{{{{C}}1}} }}{{{{C}}_{{{{C}}1}} {{Z}}}}} \right)\left( {1 - {{e}}^{{\left( {{\raise0.7ex\hbox{${{Z}}$} \!\mathord{\left/ {\vphantom {{{Z}} {{Y}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{Y}}$}}} \right)\left( {{\raise0.7ex\hbox{${{H}}$} \!\mathord{\left/ {\vphantom {{{H}} {{I}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{I}}$}}} \right)}} } \right)} \hfill \\ { + \frac{{{{mC^{\prime}}}_{{{1}}} {{C}}_{{{{C}}1}} }}{{{X}}}\left[ {{{e}}^{{\left( {\frac{{{Y}}}{{2{{X}}}}} \right)\left( {\frac{{{H}}}{{{I}}}} \right)}} \cdot \cos \left( {\frac{{{{RH}}}}{{{I}}}} \right)} \right] + \frac{{{{M}}_{2} {{C^{\prime}}}_{{{1}}} + {{M}}_{2} {{C^{\prime}}}_{{{1}}} ^{2} {{C}}_{{{{C}}1}} }}{{{{C}}_{{{{C}}1}} {{X}}}}\left[ {{{e}}^{{\left( {\frac{{{Y}}}{{2{{X}}}}} \right)\left( {\frac{{{H}}}{{{I}}}} \right)}} \cdot \sin \left( {\frac{{{{RH}}}}{{{I}}}} \right)} \right]} \hfill \\ \end{array}$$

(21)

The expressions for peak delay time and peak voltages at node C and B are discussed by Eqs. (15), (16), (20) and (21) respectively. The essential proposed crosstalk voltage and peak crosstalk noise voltage respectively at node C are discussed by Eqs. (14) and (16).

3 Simulation Result and Discussion

Figure-1 shows simulation set-up of two L type High speed RLC mutually coupled interconnection system having 1000 μm of length. High performance CPU system designs typically consist of such type of bus structures. Symmetrical Step signal having finite and equal rise/fall time of 10 ps is used to excite the aggressor line. It is assumed that the interconnection system is identical and symmetrically distributed by considering that the system is connected with identical size of inverters for drivers and loads. Variations in the input slew times values up to 200 ps are used for the simulation of Mutually coupled interconnection system connected with identical driver size.

For the testing and verification purpose, we have compared our proposed model values with BKM [19] model values to show the novelty of our proposed work. This comparison was done on the same set of circuit parameters. Our work is much-improved version of BKM model [19] for the same L-interconnect model with the consideration of mutual inductance for high operating frequencies. Comparison of simulated results at node C for the expression given by Eq. (16) for proposed model and BKM model are demonstrated in Table 1 for various input slew times. Table 2 discusses the comparison of aggressor line voltage described by Eq. (21) with BKM model values and our proposed model for the various input slew values. Comparative results for the peak times t_pc and t_pb at node C and node B of the victim line and aggressor line described by Eqs. (15) and (20) respectively is discussed in Table 3 and Table 4. Comparative results for proposed model Aggressor voltage, BKM and SPICE for different values of T_s are shown in Figs. 2, 3 and 4 respectively. Similarly, comparative results for aggressor line voltage, victim line peak time and aggressor line peak time values from proposed model and the values from SPICE simulations are shown in Figs. 5, 6, 7, 8, 9, 10, 11, 12 and 13 respectively.

Table 1 Comparative analysis for peak crosstalk noise received from proposed model and BKM [19]

Table 2 Comparative analysis for aggressor line voltage received from proposed model and BKM [19]

Table 3 Comparative analysis for victim line peak time got from proposed model and BKM [19]

Table 4 Comparative analysis for aggressor line peak time vn ‘received from proposed model and BKM [19]

Fig. 2

Comparative graph of peak crosstalk noise obtained from proposed model, SPICE and BKM with T_s = 0

Fig. 3

Comparative graph of peak crosstalk noise obtained from proposed model, SPICE and BKM with T_s = 100

Fig. 4

Comparative graph of peak crosstalk noise obtained from proposed model, SPICE and BKM with T_s = 200

Fig. 5

Comparison of aggressor line voltage obtained from proposed model, SPICE and BKM with T_s = 0

Fig. 6

Comparison of aggressor line voltage obtained from proposed model, SPICE and BKM with T_s = 100

Fig. 7

Comparison of aggressor line voltage obtained from proposed model, SPICE and BKM with T_s = 200

Fig. 8

Comparison victim line peak time obtained from proposed model, SPICE and BKM with T_s = 0

Fig. 9

Comparison victim line peak time obtained from proposed model, SPICE and BKM with T_s = 100

Fig. 10

Comparison victim line peak time obtained from proposed model, SPICE and BKM with T_s = 200

Fig. 11

Comparison of aggressor line peak time obtained from proposed model, SPICE and BKM with T_s = 0

Fig. 12

Comparison of aggressor line peak time obtained from proposed model, SPICE and BKM with T_s = 100

Fig. 13

Comparative graph of aggressor line peak time obtained from proposed model, SPICE and BKM with T_s = 200

.

After analysing the simulated result related Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10 and Tables 1, 2, 3 and 4, we can easily find out the novelty and importance of our proposed model in comparison to BKM [19] model. By considering mutual inductance in between two coupled interconnection models, our proposed model becomes more realistic and generic as it follows SPICE results better than BKM model. Deviation in between BKM model values with SPICE values is very large therefore; BKM model becomes appropriate in current scenario.

4 Conclusion

Proposed research work discussed about the mathematical analysis of delay and crosstalk voltage in mutually coupled RLC VLSI interconnection structures. The derived models for crosstalk voltage and delay are found precise as simulation results are very close to SPICE. The L-type RLC mutually coupled interconnection system is proposed in this research work. The correctness and validity of the research work is demonstrated by the simulation results. Simulation results shows that the proposed models are having less than 10% error comparable to the results obtained from the SPICE.