Vibration Analysis of Functionally Graded Material Plate

Abstract

Functionally graded materials (FGMs) are the advanced materials in the family of engineering composites made of two or more constituent phases with continuous and smoothly varying composition. Nine noded heterosis plate element is used to formulate the elastic stiffness matrix and mass matrix. The results are also extracted from Abaqus CAE by using S8R5 shell elements. Free vibration analysis is done to obtain the different modes as well as the frequencies. Harmonic sine load is applied at the centre of the FGM plate to obtain a forced vibration response. Impulse forces of rectangular, half-cycle sine, triangular shapes are applied on the top of the plate at the centre and the shock spectra of C-Si C FGM plate is plotted.

1 Introduction

The diverse and potential applications of FGMs in aerospace, medicine, defence, energy, and other industries have attracted a lot of attention recently. The application of these advanced materials was first visualized during a spaceplane project in 1984 in National Aerospace Laboratory of Japan to avoid the stress peaks at interfaces in coated panels for the space shuttle. Combination of materials used here served the purpose of a thermal barrier system capable of withstanding a surface temperature of 2000 K with a temperature gradient of 1000 K across a 10 mm thick section [1]. Later on, its applications have been expanded to also the components of chemical plants, solar energy generators, heat exchangers, nuclear reactors and high-efficiency combustion systems. The concept of FGMs has been successfully applied in thermal barrier coatings where requirements are aimed to improve thermal, oxidation and corrosion resistance. FGMs can also find application in communication and information techniques. Abrasive tools for metal and stone cutting are other important examples where the gradation of the surface layer has improved performance.

The variations of the volume fractions through the thickness are assumed to follow a power-law function. The Reissener-Mindlin first-order shear deformation theory is very much appropriate for thick plates [2]. It was taken to analyze the behaviour of the plate subjected to free and forced vibration. It has been found from the literature that not many studies are done to the vibration analysis of functionally graded plates. Reddy et al. [3] carried out the free vibration analysis of functionally graded plates. They have developed analytical formulations and solutions for the free vibration analysis of functionally graded plates using higher-order shear deformation theory (HSDT). The principle of virtual work was used to derive the equations of equilibrium and boundary conditions. Navier’s technique was used to obtain the solutions for FGM plates. Vimal et al. [4] have studied the free vibration analysis of functionally graded skew plates using the finite element method. The first-order shear deformation plate theory is used to consider the transverse shear effect and rotary inertia. The properties of functionally graded skew plates are assumed to vary through the thickness according to a power law. It is found that when the length to thickness ratio of functionally graded skew plates increases beyond 25, the variation in the frequency parameter is very negligible and also found that a volume fraction exponent that ranges between 0 and 5 has a significant influence on the frequency. Gulshan et al. [5] carried out a free vibration analysis of functionally graded material (FGM) skew plates subjected to the thermal environment. It was concluded that the volume fraction index and skew angle plays an important role in predicting the vibration of FGM skew plate subjected to thermal load.

Reddy [6] have studied theoretical formulation and FEM model based on TSDT for FGM plate. The formulation accounted for thermo-mechanical effects combining change with time and geometric nonlinearity. In this higher-order theory, transverse shear stress was expressed as a quadratic function along with the depth. Hence this theory requires no shear correction factor. The plate was considered as the homogenous and material composition was varied along with the thickness. The Young’s modulus was assumed to vary as per rule of the mixture in terms of the volume fractions of the material constituents. Hughes and Cohen [7] developed the heterosis element and elemental equation. They derived lumped positive definite mass matrix, element matrix and load vector and method for finding critical time step. High-accuracy finite element for thick and thin plate bending is developed, based upon Mindlin plate theory.

It has been found from the literature survey that not many researchers attempted to the vibration analysis of functionally graded plates. Further, we observed that many authors could model such problems with a stepped variation in material properties instead of continuous variation. This would have happened because of the limitations of the commercial software available. In this context, we felt that MATLAB code could be used for tailoring the continuous variation in material properties in FE Modelling. Hence MATLAB code was developed for vibration analysis of FG plate. The analysis was carried out for C-Si C FGM plate with different volume fraction indices. The results are compared with Abaqus CAE by using S8R5 shell elements.

2 Problem Formulation

First-order shear deformation theory is used for plate formulation. Displacement variation is linear, across the plate thickness. But there is no change in plate thickness during deformation. A further assumption is that the normal stress across the thickness is neglected. Properties are graded through the thickness direction which follows a volume fraction power-law distribution. The different elements of the plate are expected to undergo translational and rotational displacement. In the present work 9- noded heterosis element is used to discretize the plate.

2.1 Strain-Displacement Relations

The displacement field at any arbitrary distance z from the midplane based on the first-order shear deformation plate theory is given by

$$ \begin{aligned} \left[ {\bar{u}_{p} (x,y,z), \, \bar{v}_{p} (x,y,z),\bar{w}_{p} ( {\text{x,y,z)}}} \right] & = \, \left[ {u_{0} (x,y), \, v_{0} (x,y),w_{0} (x,y) \, } \right] \\ \quad + {\text{ z}}\left[ {\theta_{x} (x,y), \, \theta_{y} (x,y),0 \, } \right] \, \\ \end{aligned} $$

(1)

where, u̅_p, v̅_p, w̅_p are displacements in x, y and z directions respectively, u₀, v₀ and w₀ are the associated midplane displacements along x, y and z axes respectively and θ_x and θ_y are the rotations about y and x-axes respectively.

The linear strain displacement relations are given by

$$ \begin{aligned} & \varepsilon_{xl} = u_{0,x} + z\chi_{x} \, \\ & \varepsilon_{yl} = v_{0,y} + z\chi_{y} \\ & \gamma_{xyl} = u_{0,y} + v_{0,x} + z\chi_{xy} \, \\ & \gamma_{xzl} = w_{0,x} + \theta_{x} \, \\ & \gamma_{yzl} = w_{0,y} + \theta_{y} \\ \end{aligned} $$

(2)

where, ε_xl, ε_yl and γ_xyl are the linear in-plane normal and shear strains, γ_xzl and γ_xzl are transverse shear strains, z is the distance of any layer from the middle plane of the plate and χ are the curvatures.

$$ \left\{ \chi \right\} = \left\{ {\begin{array}{*{20}c} {\chi_{x} } \\ {\chi_{y} } \\ {\chi_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial \theta x}{\partial x}} \\ {\frac{\partial \theta y}{\partial y}} \\ {\frac{\partial \theta x}{\partial y} + \frac{\partial \theta y}{\partial x}} \\ \end{array} } \right\} $$

(3)

The strain-displacement field at any distance z as shown in Fig. 1.

Fig. 1

Deformed and un-deformed beam

2.2 Finite Element Formulation

In the current work, the FGM plate has been discretized using 9-noded heterosis element with 5-degree of freedom (dofs) at all the edge nodes and 4 dofs at the internal node as shown in the Fig. 2. The serendipity shape functions have been used for the transverse dofs, w, and Lagrange shape function are used in the remaining dofs, u, v, θ _x, and θ _y

Fig. 2

Nodal configuration of the plate element

Resultant Forces and moments. The analysis of FGM plate is carried out to establish the relation between the forces and strains by considering transverse shear terms.

Constitutive matrix of the isotropic plate is

$$ Q = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{11} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right] $$

(4)

where,

$$ Q_{11} = \frac{E}{{1 - \nu^{2} }},\begin{array}{*{20}c} {} & {} \\ \end{array} Q_{12} = \frac{\nu E}{{1 - \nu^{2} }},\begin{array}{*{20}c} {} & {} \\ \end{array} Q_{66} = \frac{E}{{2\left( {1 + \nu } \right)}} $$

The material properties P_Z (Elastic constants E,$\nu$, density) at distance, z from the middle surface of the plate is

$$ P_{z} = P_{b} + \, \left( {P_{t} - P_{b} } \right)\left[ {\frac{{\left( {2z + h} \right)}}{2h}} \right]^{k} = \, P_{b} + \, \left( {P_{t} - P_{b} } \right)Vf $$

(5)

where, h is the plate thickness, t and b denotes the top and the bottom surface $\left( { \pm \, z/2} \right)$, k is material volume fraction index, V_f is volume fraction.

Stress-strain relationship is

$$ \left\{ \sigma \right\} = \, \left[ Q \right]\left\{ \varepsilon \right\} $$

(6)

where, $\left\{ \sigma \right\}{ = }\,\mathop {\left\{ {\begin{array}{*{20}c} {\sigma_{x} ,} & {\sigma_{y} ,} & {\tau_{xy} } \\ \end{array} } \right\}}\nolimits^{T} { , }\varepsilon \,{ = }\varepsilon_{0} + {\text{z}}\chi$.

The in-plane resultant forces and moments in the kth layer are evaluated as

$$ \left\{ {\begin{array}{*{20}c} {N,} & {M \, } \\ \end{array} } \right\}{ = }\sum\limits_{k = 1}^{N} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ {\sigma \, } \right\}} } \left( {\begin{array}{*{20}c} {1,} & {z \, } \\ \end{array} } \right)dz $$

(7)

Resultant Transverse Shear Force on the kth layer is given by

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} {Q_{xz} } \\ {Q_{yz} } \\ \end{array} } \right] = \sum\limits_{k = 1}^{N} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ {\begin{array}{*{20}c} {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\} \, dz} } = \sum\limits_{k = 1}^{N} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left[ {\begin{array}{*{20}c} {Q_{44} } & {Q_{45} } \\ {Q_{45} } & {Q_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} \, dz} } \hfill \\ \hfill \\ \end{aligned} $$

(8)

$$ \begin{aligned} & Q_{44} = \left( {G_{13t} - G_{13b} } \right)\left[ {\frac{{\left( {2z + h} \right)}}{2h}} \right]^{k} + G_{13b} \\ & Q_{55} = \left( {G_{23t} - G_{23b} } \right)\left[ {\frac{{\left( {2z + h} \right)}}{2h}} \right]^{k} + G_{23b} \\ & Q_{45} = 0 \\ \end{aligned} $$

(9)

The constitutive relation for FGM plate is given by

$$ \left\{ N \right\} = \, \left[ C \right]\left\{ \varepsilon \right\} \, $$

(10)

where, $\left\{ N \right\} = \left[ {\begin{array}{*{20}c} {Nx,} & {Ny,} & {Nxy,} & {Mx,} & {My,} & {Mxy,} & {Qxz,} & {Qyz} \\ \end{array} } \right]^{T}$ represents the in-plane stress resultants (N), out of plane bending moments (M) and shear resultants (Q). Here, [C] is the constitutive matrix [8] of the FGM plate. To compensate for the parabolic shear stress variation across the thickness of the plate, a correction factor of 5/6 is used in the shear-shear coupling components of the constitutive matrix [9]. Using Green-Lagrange’s strain-displacement expression [10], the linear strain-displacement matrix[B] have been worked out.

The different participating element-level matrices such as elastic stiffness matrix $\left[ {ke} \right]$, and consistent mass matrix $\left[ {me} \right]$ have been derived using corresponding energy expression.

The element elastic stiffness matrix and element mass matrix are derived using the following relations

$$ \left[ {ke} \right] = \int\limits_{ - 1}^{1} {} \int\limits_{ - 1}^{1} {} \left[ B \right]^{T} \left[ C \right]\left[ B \right]\left| J \right|d\varepsilon d\eta \, $$

(11)

$$ \left[ {me} \right] = \int\limits_{ - 1}^{1} {} \int\limits_{ - 1}^{1} {} \left[ {\bar{N}} \right]^{T} \left[ I \right]\left[ {\bar{N}} \right]\left| J \right|d\varepsilon d\eta \, $$

(12)

In which, [I] is the inertia matrix

Computer coding and Implementation. To perform all the computations, a computer program is developed using MATLAB to implement the finite element formulation and include all the necessary parameters to investigate the vibration behaviour of the FGM plate.

In the present code, selective integration scheme is incorporated for the generation of the element stiffness matrix. The 3 × 3 Gauss quadrature rule is adopted to get the bending terms and 2 × 2 Gauss rule is used to solve shear terms in order to avoid possible shear locking. The mass matrix is evaluated by using 3 × 3 Gauss rule [11].

2.3 Formulation of Dynamic Problems

Validation of assembled stiffness matrix is done through bending problems and that of mass matrix is done through vibration problems. In order to validate the formulation of mass matrix, one has to solve a free vibration problem by incorporating the validated elastic stiffness matrix. The standard governing equation in matrix form for the deflection problem is

$$ \left[ {K_{e} } \right]\left\{ q \right\} = \left\{ P \right\} $$

(13)

$\left\{ P \right\}$ is the nodal load vector, $\left[ {K_{e} } \right]$ is the system elastic stiffness matrix. For a given set of loads, the displacement $\left\{ q \right\}$ can be determined using the above equation. If the displacement vector is validated, it ensures the correctness of formulation and coding of the stiffness matrix.

The standard governing equation in matrix form for the free vibration problem is

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + + \left[ {K_{e} } \right]\left\{ q \right\} = \left\{ P \right\} $$

(14)

The standard governing equation in matrix form for the force vibration problem is

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + \left[ C \right]\left\{ {\dot{q}} \right\} + \left[ {K_{e} } \right]\left\{ q \right\} = \left\{ P \right\} $$

(15)

$\left[ M \right] ,\,\left[ {K_{e} } \right]$ and $\left[ C \right]$ represents global mass matrix, global stiffness matrix and damping matrix respectively.

$$ \left[ C \right] = \alpha \left[ M \right] + \beta \left[ {K_{e} } \right] $$

(16)

where, $\alpha$ $\beta$ and are the Rayleigh damping coefficients. From this, we can solve the forced vibration problem. From this, we can solve the force vibration problem using Newmark-beta method.

Newmark-beta technique. The problem is solved here by using constant acceleration method as it is unconditionally stable. The stability criteria for constant acceleration method is given by

$$ \frac{\Delta t}{{\mathop T\nolimits_{n} }} \le \frac{1}{\pi \sqrt 2 }\frac{1}{{\pi \sqrt {\gamma - 2\beta } }} $$

$$ {\text{For }}\gamma = \frac{1}{2}{\text{and }}\beta = \frac{1}{4}{\text{this condition becomes}}\,\,\frac{\Delta t}{{\mathop T\nolimits_{n} }}{ < }\infty $$

3 Results and Discussion

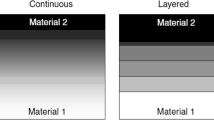
The properties of FGM plates are graded through the thickness direction according to a volume fraction power law distribution (Fig. 3).

Fig. 3

Variation of volume fraction with the non-dimensional thickness

3.1 Free Vibration Analysis

The heterosis element is used in the code for free vibration analysis. For validation of the present code, the data available for the functionally graded plate aluminium oxide –titanium alloy of size 0.4 m × 0.4 m × 0.005 m available in the literature of He et al. [12] is used. In numerical simulation by Abaqus, S8R5 element has been used. Table 1 shows the material properties. Table 2 validated the code with literature and simulation.

Table 1 Material properties of Aluminium Oxide–Titanium alloy FGM plate

Table 2 Variation of fundamental frequency with k values –simply supported plate-comparison

The present code is validated with results of He et al. (2001). The simulation results are also in good agreement with results obtained from FEM coding. This ensures the correctness of the formulation of the stiffness and mass matrix.

3.2 Free Vibration Analysis of C-Si C Plate

The analysis is done for C-Si C plate (0.5 × 0.5 × 0.001 m). Material properties are given in Table 3. Convergence results are shown in Fig. 4. First four mode of vibration shown in Fig. 5. Frequency of Vibration is minimum for carbon plate as shown in Table 4.

Table 3 Material properties C-Si C FGM plate

Fig. 4

Convergence of fundamental frequency of simply supported C-Si C FGM plate (k = 2)

Fig. 5

First 4 mode shapes of simply supported C-Si C FGM plate (k = 2)-Simulation

Table 4 Variation of the natural frequencies (Hz) of FGM simply supported Square Plate for different k values. 22 × 22 mesh-Heterosis element(FEM)

3.3 Forced Vibration Analysis

Forced vibration analysis was carried out at the centre of the plate using harmonic sine loading and different impulse loadings.

Harmonic Sine Wave Loading. A harmonic force P(t) = P₀ sin($\omega t$) load is applied at the centre of the plate, where P₀ is the amplitude or peak value of the force and $\omega$ is the forcing frequency. $T = 2\pi /\omega$ is the forcing period of the FGM plate P₀ = 1 N and $\omega$ = $2\pi f$ where $\omega$ is circular frequency and ${\text{f}}$ is natural frequency of the Plate. Figure 6 shows that maximum displacement at the centre of the plate increases with the material index (k value). Table 5 compares the un-damped and damped cases.

Fig. 6

Response of simply supported C-Si C FGM plate subjected to harmonic loading

Table 5 Displacement of simply supported C-Si C plate for different k values

Impulse loading. A very large force that acts for a very short time but with a time integral that is finite is called an impulse force. Impulse forces of rectangular, half-cycle sine, triangular shapes each with the same value of maximum force 1 N is applied at the centre of the plate The response behavior of FGM plate is studied for material index(k) value = 2. t_d is pulse duration. T_n is the natural time period of vibration of the plate and u _st0 is the static deflection of the plate. Static deflection is 1.438e-4 m and Natural time period is 0.0365 s. The shock spectra of the FGM plate with material index k = 2 is shown in Fig. 7. Variation of response factor with td/T n, for k = 2 is given in Table 6. The present results are in good agreement with the available literature [13].

Fig. 7

Shock spectra of simply supported C-Si C FGM Plate (material index k = 2)

Table 6 Variation of deformation response factor (R_d) with td/T n values (k = 2)

4 Conclusions

In the present investigation, a finite element formulation is developed for vibration analysis of FGM plates. The analysis is carried out by developing a computer program in MATLAB. A 9- noded heterosis element is used to model the FGM plate. The heterosis element exhibits improved characteristics as compared to the 8- noded serendipity and 9-noded Lagrange elements. It offers a high level of accuracy for extremely thin plate configurations. Convergence study has been carried out for ensuring the convergence of the numerical results. The results are also extracted from Abaqus CAE by using S8R5 shell elements and are in very good agreement with the developed elements. Free vibration analysis is done to study the different modes as well as frequencies. It is observed that free vibration response is minimum for carbon and maximum for Silicon carbide plate. The central deflection of the plate increases with increase in volume fraction index for all types of boundary conditions. From the shock spectra, it is clearly understood that if the pulse duration (t_d) is longer than T_n/2, the overall maximum deformation occurs during the pulse. Then the pulse shape is of great significance. For the larger value of t_d/T_n, the overall maximum deformation is influenced by the rapidity of the loading. The rectangular pulse in which the force increases suddenly from zero to maximum show the large deformation. The triangular pulse in which the increase in the force is initially slowest among the three pulses produces the smallest deformation. The half-cycle sine pulse in which the force initially increases at an intermediate rate causes deformation that for many values of t_d/T_n is larger than the response of the triangular pulse.