Keywords

1 Introduction

As one of the most challenging classification tasks in computer vision and pattern recognition, face recognition have attracted much researchers’ attentions [1,2,3,4]. Many face recognition techniques have been proposed in the past few decades. A face image of size pixels is usually represented by a dimensional vector. However, excessive high dimensionality has an impact on the efficiency and accuracy of face recognition. In the face of this situation, the method of feature extraction or data dimensionality reduction is generally adopted. The classic dimensionality reduction methods mainly include PCA, LDA, etc. Although these methods can reduce the dimension of the original data well, there is no non-negative requirement for the decomposition factor, so there are negative values in the decomposed components. These negative values have no physical significance in practical problems. Therefore, NMF is generated by operation.

In 1999, Non-negative matrix decomposition (NMF) algorithm was first proposed by Lee in Nature [5]. Its purpose is to approximate decompose the original nonnegative data matrix into the product of two matrices with nonnegative elements, namely basis matrix and coefficient feature matrix. This part-based, purely additive nature of the NMF method can enhance the partial to overall interpretation of the data. Because of its non-negative constraints, sparse local expression and good interpretability, the NMF has been widely used in many real world problems such as face recognition, text clustering, feature recognition and information retrieval [6,7,8].

Many scholars have improved NMF and applied it in the field of face feature extraction and classification recognition. In 2002, Hoyer [9] integrated the idea of sparse coding into NMF, using L1 norm as sparse penalty term, and using Euclidean distance to calculate the error between the original data and the reconstructed data. To use the data geometric structure, Cai et al. [10] proposed a graph regularization non-negative matrix factorization (GNMF). In the GNMF algorithm, the geometrical structure of data is encoded by a k-nearest neighbor graph. In order to maintain the internal structure of the original data, Qing et al. proposed another variant of NMF, which is called a graph regularization non-negative matrix factorization (GNMF) method to describe the internal manifold structure of data points in the data matrix by constructing the neighborhood graph [11]. In order to improve the sparsity of the decomposition results and transmit the effective information, Jiang Wei et al. Proposed the sparse constraint graph NMF method (SGNMF) [12]. Zhou et al. Proposed the NMF algorithm based on Gabor wavelet by combining wavelet change and manifold [13].

With single figure to constraints of the internal structure of the original data, although to a certain extent to meet the demand of feature vector, but the results were not intellectual and meet the requirements of the single, while there are double or more constraints of the NMF algorithm, but while in measuring loss function based on L2 norm, existing algorithms are sensitive to noise and outliers caused by sparse decomposition results, and poor robustness problems. Therefore, this paper proposes a multi-graph regularized non-negative matrix factorization method based on L2,1 norm (L2,1-MGNMF). The method uses the line sparse property of L2,1 norm as the loss function. On the basis of the single graph regularization structure, the manifold structure of the original data is represented by fusing multiple graphs, and the constraints and decomposition results of the original structure of the original data are considered. Increased sparsity and robustness. The proposed L2,1-MGNMF method is finally tested on ORL and other face databases. A lot of experimental results show that our L2,1-MGNMF approach is effective and feasible, which surpasses some existing methods.

The remainder of the paper is organized as follows: Sect. 2 introduces the basic ideas of the existing NMF and GDNMF methods. Section 3 proposes our L2,1-MGNMF and gives theoretic analysis. Experimental comparisons are reported in Sect. 4. Finally, conclusions are given in Sect. 5.

2 A Brief Review of NMF

This section describes NMF and GNMF algorithms briefly. Let X be a training data matrix of \( m \times n \)-dimensional samples \( x_{1} ,x_{2} , \cdots ,x_{n} ,\,i.e.,\,x \in {\mathcal{R}}^{m \times n} \) with nonnegative entries. Each column of X represents a face image with m dimensions.

2.1 Non-negative Matrix Factorization(NMF)

NMF aims to approximately decomposes the training sample matrix X into a product of two non-negative matrices \( A \in {\mathcal{R}}^{m \times r} \) and \( S \in {\mathcal{R}}^{r \times n} \) (r ≪ min (m, n)), i.e., X ≈ AS. Matrices A and S are called basis matrix and coefficient matrix, respectively. In general, NMF is based on minimizing the Euclidean distance between X and AS. The corresponding optimization problem is as follows:

$$ \mathop {min}\limits_{A,S} \left\| {X - AS} \right\|_{F}^{2} ,\,s.t.\,A \ge 0,S \ge 0 $$
(1)

where ‖•‖F is the matrix Frobenius norm of a matrix. The optimization problem can be solved using gradient descent method. The well-known multiplicative update rules are as follows:

$$ S^{{\left( {t + 1} \right)}} \leftarrow S^{\left( t \right)} \frac{{\left( {A^{{\left( t \right)^{T} }} X} \right)}}{{\left( {A^{{\left( t \right)^{T} }} A^{\left( t \right)} S^{\left( t \right)} } \right)}}\quad \quad \quad A^{{\left( {t + 1} \right)}} \leftarrow A^{\left( t \right)} \frac{{\left( {XS^{{\left( t \right)^{T} }} } \right)}}{{\left( {AS^{\left( t \right)} S^{{\left( t \right)^{T} }} } \right)}} $$
(2)

The convergence of these multiplicative update rules have been proved in [14].

2.2 Graph Regularized Non-negative Matrix Factorization (GNMF)

To find a compact representation which uncovers the hidden semantics and simultaneously respects the intrinsic geometric structure, the graph regularized non-negative matrix factorization (GNMF) was proposed in [10]. GNMF solved the following optimization problem:

$$ \mathop {min}\limits_{A,S} \left\| {X - AS} \right\|_{F}^{2} + {\uplambda} Tr\left( {SLS^{T} } \right),\,s.t.\,A \ge 0,S \ge 0 $$
(3)

where \( Tr\left( \bullet \right) \) is the trace of a matrix and \( L = D - W \) is called the graph Laplacian matrix, regularization parameter \( \lambda \ge 0 \) controls the smoothness of the new representation. The W denotes the weight matrix, and D is a diagonal matrix. The corresponding multiplicative update rules for solving Eq. (3) are as follows:

$$ S^{{\left( {t + 1} \right)}} \leftarrow S^{\left( t \right)} \frac{{\left( {X^{{\left( t \right)^{T} }} A + {\uplambda} WS} \right)}}{{\left( {A^{{\left( t \right)^{T} }} A^{\left( t \right)} S^{\left( t \right)} } \right)}}\quad \quad A^{{\left( {t + 1} \right)}} \leftarrow A^{\left( t \right)} \frac{{\left( {XS^{{\left( t \right)^{T} }} } \right)}}{{\left( {AS^{\left( t \right)} S^{{\left( t \right)^{T} }} } \right)}} $$
(4)

3 Multiple Graph Regularized Non-negative Matrix Factorization Based on L2,1 Norm (L2,1-MGNMF)

Although the existing NMF-based improved methods have achieved good results, they still have some limitations. In this section, we will describe our Multiple Graph Regularized Non-negative Matrix Factorization based on L2,1 Norm (L2,1-MGNMF). Further we formulate our optimization problem by adding supervised label information to the objective function of L2,1-MGNMF. The definition and update rules of L2,1-MGNMF are given below.

3.1 L2,1-MGNMF Model

In order to maintain the original structure of the data as much as possible, this paper uses the neighborhood weighting, weight weighting, and sparse weighting to constrain the structure of the original data. The three weight matrices are defined as follows:

  1. 1.

    Neighborhood weighting. \( W_{ij}^{N} = 1 \) if and only if sample j is the nearest neighbor of sample i. This is the simplest weighting method and is very easy to compute.

  2. 2.

    Weight weighting. If sample j is the neighbor of sample i, then

    $$ W_{ji}^{W} = exp(\frac{{ - \left\| {x_{i} - x_{j} } \right\|^{2} }}{{2\sigma^{2} }}) $$
    (5)
  3. 3.

    Sparse weighting. Sparse weight graphs can represent the sparse structure of the original data, and the sparse constraint is added to make the base image obtained by the decomposition represent the original image with as few features as possible, the weight matrix defined by:

    $$ W^{S} = s.t.\,\left\| {x - D\varphi } \right\|_{p} \le \varepsilon , $$
    (6)

    where \( \varphi \) is the sparse coefficient.

The L2,1-MGNMF solves the following optimization problem:

$$ \begin{aligned} & \mathop {min}\limits_{A,S} \left\| {X - AS} \right\|_{2,1} + \alpha \mathop \sum \limits_{x = 1}^{X} \mu_{x} \left( {\mathop \sum \limits_{i,j = 1}^{m} \left\| {s_{i} - s_{j} } \right\|_{2}^{2} w_{ij}^{x} } \right) + \beta \left\| \mu \right\|_{2}^{2} , \\ & s.t.\,A \ge 0,S \ge 0,\mathop \sum \limits_{x = 1}^{X} \mu_{x} = 1,\mu \ge 0 \\ \end{aligned} $$
(7)

where, \( W^{X} \) represents the x-th weight graph, and \( \alpha \) and \( \beta \) are balance parameters. The discrimination ability of different graphs is very different. The weight \( \mu \) should be set according to the graph, and the balance parameter \( \alpha \) determines the influence of the integrated manifold structure on the objective function.

3.2 The Update Rules of L2,1-MGNMF

Though the objective function in Eq. (7) is not jointly convex in the pair (A, S, \( \mu \)), it is convex with respect to one variable in the (A, S, \( \mu \)) while fixing the others. Therefore it is unrealistic to expect an algorithm to find the global minima. In the following, we can use the iterative solution of fixing two variables to update another variable which can achieve local minima. The solution process is as follows:

  1. 1.

    Fix \( \mu \) and S, update A. To remove the irrelevant items, the optimization problem of A can be transformed into the following:

    $$ \begin{aligned} min\left\| {X - AS} \right\|_{2,1} = & \,tr((X - AS)D(X - AS)^{T} ) \\ = & \,tr\left( {XDX^{T} - 2ASDX^{T} + ASDS^{T} A^{T} } \right) \\ & s.t.\,A \ge 0 \\ \end{aligned} $$
    (8)

    where D is a diagonal matrix \( d_{ii} = 1/\left\| {x_{i} - As_{i} } \right\| \).

  2. 2.

    Let \( \Lambda \) be the Lagrange multiplier, the Lagrange \( \ell \) is:

    (9)
  3. 3.

    The partial derivatives of \( \ell \) with Eq. (9) is:

    $$ \frac{{\partial \ell \left( {A,\Lambda } \right)}}{\partial A} = - 2XDS^{T} + 2ASDS^{T} + {\uplambda}{\Lambda} = 0 $$
    (10)
  4. 4.

    Using the KKT conditions \( \Lambda _{ij} A_{ij} = 0 \), we get the following equations:

    $$ \left( { - 2XDS^{T} + 2ASDS^{T} } \right)A_{ij} = 0 $$
    (11)
  5. 5.

    Fix \( \mu \) and A, update S. To remove the irrelevant items, the optimization problem of S can be transformed into the following:

    $$ min\left\| {X - AS} \right\|_{2,1} + \alpha \sum\nolimits_{x = 1}^{X} {\mu_{x} \left( {\sum\nolimits_{i,j = 1}^{m} {\left\| {s_{i} - s_{j} } \right\|_{2}^{2} w_{ij}^{x} } } \right).\quad s.t.\,S \ge 0} $$
    (12)
  6. 6.

    Similarly, we get the following equations:

    $$ \left( { - 2A^{T} XD + 2A^{T} ASD + \alpha SL} \right)S_{ij} = 0 $$
    (13)

    Where \( L = \sum\nolimits_{x = 1}^{X} {\mu_{x} L^{x} } \).

  7. 7.

    Therefore, according to Eq. (11) and Eq. (13), we have the following updating rules:

    $$ A^{{\left( {t + 1} \right)}} \leftarrow A^{\left( t \right)} \frac{{(XDS^{T} )^{\left( t \right)} }}{{(ASDS^{T} )^{\left( t \right)} }} $$
    (14)
    $$ S^{{\left( {t + 1} \right)}} \leftarrow S^{\left( t \right)} \frac{{(A^{T} XD)^{\left( t \right)} }}{{(A^{T} ASDS + \alpha SL)^{\left( t \right)} }} $$
    (15)

Theorem 1:

The objective function \( {\rm O}_{1} \) in Eq. (7) is non-increasing under the updating rules in Eq. (14), and (15).

We can iteratively update A and S until the objective value of \( {\rm O}_{1} \) does not change or the number of iteration exceed the maximum value. Theorem 1 also guarantees that the multiplicative updating rules in Eq. (14) and (15) converge to a local optimum.

We summarize our Multiple Graph Regularized Non-negative Matrix Factorization based on L2,1 Norm (L2,1-MGNMF) algorithm in Table 1.

Table 1. The algorithm of L2,1-MGNMF
Full size table

4 Experimental Results

In this section, we compare the proposed L2,1-MGNMF with four representative algorithms, which are NMF, SGNMF, LGNMF [15], and SPGNMF [16], on three face datasets, i.e., ORL [17], Yale [18], and PIE [19].

4.1 Dataset

Three datasets are used in the experiment. The important statistics of these data sets are summarized in Table 2. Figure 1 shows example images of ORL, Yale, and PIE datasets. Before the experiment, face image should be preprocessed. We think that the texture region contains more information, and the rest of the region is redundant. Therefore, the texture rich region is reserved for future experiments (see Fig. 2). Then, each face image is represented as a column vector and the features (pixel values) are then scaled to [0, 1] (divided by 255).

For each sample, we randomly select half of the images as the training set and the rest as the test set. Repeat random selection l times to ensure that 95% of the images have participated in the training and testing. The performance of L2,1-MGNMF is measured by Accuracy (ACC) and False Acceptance Rate (FAR).

Table 2. Statistics of the four datasets
Full size table
Fig. 1.
figure 1

Face image examples of the (a) ORL, (b) Yale, and (c) PIE datasets

Full size image
Fig. 2.
figure 2

Pre-processed image examples

Full size image

4.2 Parameter Selection

The main parameters in the algorithm model are the dimension rafter dimension reduction, the iteration number Lit which affects the convergence speed of the algorithm, and balance parameters \( \alpha \) which affects the decomposition error.

Figure 3 shows the accuracy curve when Lit values 100, 300, 500, 800 and 1500 respectively. It can be seen from the figure that the performance of the algorithm increases with the number of iterations. Considering the relationship between accuracy and computational efficiency, Lit is set to 1500.

Fig. 3.
figure 3

The ACC with different Lit

Full size image

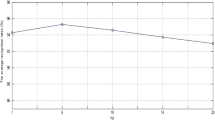
It can be seen from the figure that the performance of the algorithm increases with the decrease of the balance factor \( \alpha \). when \( \alpha < 0.01 \), the performance of the algorithm fails to further improve, so the balance parameters in this paper is 0.01 (Fig. 4).

Fig. 4.
figure 4

The ACC with different \( \alpha \)

Full size image

4.3 Compared Algorithms

To demonstrate how our approach improves performance, we compared the following four popular algorithms: NMF, SGNMF, LGNMF, and SPGNMF.

Figure 5 gives that the average accuracy versus the dimension of the subspace. Figure 6 gives that the average FAR versus the dimension of the subspace. According to Fig. 5 and 6, it can be seen that the performance of the proposed method on three face databases is significantly higher than that of other methods.

Fig. 5.
figure 5

Face predictive accuracy on the (a) ORL, (b) Yale, and (c) PIE datasets

Full size image
Fig. 6.
figure 6

The FAR on the (a) ORL, (b) Yale, and (c) PIE datasets

Full size image

Finally, we compared the sparsity of the matrix decomposition results of these five algorithms, and selected the base image obtained by the decomposition of the original data X. The feature dimension of the base image was set at 30, and the sparsity is defined by:

$$ SP\left( x \right) = \frac{{\sqrt m - \left( {\sum \left| {x_{i} } \right|} \right)/\sqrt {\sum x_{i}^{2} } }}{\sqrt n - 1} $$
(16)

where m is the dimension of the vector. When there is only one non-zero element, \( SP = 1 \), the smaller the value of SP, the denser the vector x, otherwise, the sparser. The experimental results are as follows (Table 3):

Table 3. The SP of different algorithm
Full size table

It can be seen from the table that compared with the sparsity results of these algorithms, the NMF algorithm has the worst sparsity. In this paper, L2,1-mgnmf algorithm has the highest result than other algorithms, and the decomposed base image is the most sparse with better local expression ability.

5 Conclusions

We have presented an efficient method for matrix factorization, called Multi-graph regularized Non-negative Matrix Factorization method based on L2,1 norm (L2,1-MGNMF). As a result, L2,1-MGNMF can have more discriminative power than the conventional NMF and its several variants. Further, we show the corresponding multiplicative update rules and convergence studies. Evaluations on three face datasets have revealed both higher recognition accuracy, sparsity and lower false acceptance rate of the proposed algorithm in comparison to those of the state-of-the-art algorithms. But how to build a multi-graph fusion model is still the focus of future research.