Keywords

1 Introduction

The author comes from a lower middle-income farming family in rural South India. As the youngest of five children, he was the first in his family to go beyond high school. During summer holidays, he used to help his father on the farm, which prepared him to be a hard worker, diligent, and thorough. He went through a five-year integrated Bachelor of Engineering degree in India that prepared him with a broader engineering background and helped him in the later years to work not only in solid and structural mechanics but also in heat transfer, fluid mechanics, and applied mathematics.

The author went to USA in the spring of 1969 to do a M.S. at Oklahoma State University. The he joined Professor J.T. Oden’s research group at the University of Alabama in Huntsville for Ph.D. in engineering mechanics. Professor Oden was one of the top researchers in the world and the only engineer who was beginning to work on mathematical foundations of the finite element method. The author’s dissertation topic was on the existence and uniqueness of mixed finite element approximations of boundary value problems as well as the unification of variational principles of theoretical mechanics. Both of the topics led, in addition to several journal papers, to two books with Dr. Oden.

Following his Ph.D. (1974), he worked for a brief period with Lockheed Missiles and Space Company, where he worked on a NASA (Glenn) research project to develop a 3D finite element code to study hypervelocity impact, he joined the University of Oklahoma, Norman, in January 1975. It was there where he was introduced to the subject of composite materials and structures by Professor Charles Bert that would change the course of his professional career and follow the legacy of Timoshenko and Mindlin and likes to develop shear deformation theories. Knowing the limitations of classical thin plate and shell theories in capturing inter-laminar stresses, he started working on shear deformation theories for composite laminates. His background in mathematics, mechanics, and the finite element method enabled him not only to conceive novel and improved mathematical models of beam, plate, and shell theories, but also to develop locking-free and robust finite element models – an activity that continues to the present day.

During the last four decades (he was at Virginia Tech for 12 years and 27 years and going at Texas A&M University), the author has been working on two major fronts as far as the structural mechanics is concerned (he also has also worked in computational fluid dynamics) with two topics: (1) development of 7-, 8-, and 12-parameter shell theories and their finite elements and (2) nonlocal and non-classical continuum mechanics. The first topic is a continuation of many years of his work on shear deformation theories of plates and shells to develop locking-free shell elements for large deformation analysis of laminated composite and functionally graded structures. He has collaborated with Professor C.M. Wang of the National University of Singapore (now at the University of Queensland, Australia) to develop algebraic relations between the bending, frequency, and buckling solutions of shear deformation theories in terms of the corresponding solutions of the classical theories. The second topic is a rejuvenation of ideas originated and advanced by Cosserat bothers, Green, Naghdi, Mindlin, Eringen, Hutchinson, and likes, and their implementation into structural theories. These include: couple stress theories, strain and stress gradient theories, and micromorphic theories. The nonlocal and non-classical continuum ideas can be used to study architected materials and efficient modelling of large or mega structures, by bringing material as well as structural length scales into structural theories.

In this written paper, (1) the robust shell finite elements and (2) nonlocal (micropolar) plate models are discussed. However, the oral presentation will briefly discuss all 6 milestones.

2 Robust Shell Element with Thickness Stretch

2.1 Introduction

Shear deformation theories based on the assumption of inextensibility of lines normal to the shell surface and subsequent neglect of transverse normal stress are not accurate, when a considerable thickness deformation occurs (e.g., shells made of soft materials like rubber or biological materials, where large deformations can be found), even in the linear material regime (see [1]). A simple theory that allows for thickness stretch is the seven-parameter formulation presented by Büchter et al. [5], Sansour [15], and Bischoff and Ramm [4], where the transverse displacement is expanded up to quadratic terms, and the Poisson locking is mitigated when three-dimensional constitutive equations are used. Later, Arciniega and Reddy [2] developed a tensor-based finite element shell with first-order shear deformation kinematics and seven parameters. A similar theory was presented by Payette and Reddy [14], where continuous shell elements in conjunction with high-order spectral/hp functions were used. In recent works, Gutierrez Rivera and Reddy [8] extended the formulation to transient analysis. A linear shell theory which takes thickness stretch into account has been developed by Carrera et al. [6]. In recent works, Amabili [1] introduced a geometrically nonlinear shell theory allowing third-order thickness stretch, higher-order shear deformation, and rotary inertia by using eight independent parameters. Based on the formulation presented in Amabili [1], Gutierrez Rivera et al. [9] presented a 12-parameter shell element for large deformation analysis of shell structures.

2.2 Displacement Field of the 8-Parameter Theory

Here we present few results using a third-order thickness stretching theory with eight independent parameters as an alternative to the twelve-parameter formulation. The displacement vector is assumed to be of the form

$${\mathbf{u}}(\xi^{i} ) = \underline{{\mathbf{u}}} (\xi^{\alpha } ) + \xi^{3} \frac{{\text{h}}}{2}{{\mathbf{\upvarphi}}}(\xi^{\alpha } ) + (\xi^{3} )^{2} \frac{{\text{h}}}{2}\Psi (\xi^{\alpha } ){\hat{\textbf{n}}} + (\xi^{3} )^{3} \frac{{\text{h}}}{2}\gamma (\xi^{\alpha } ){\hat{\textbf{n}}}$$
(1)

Here \(\underline{{\mathbf{u}}}\) denotes the mid-plane displacement vector \({\mathbf{\upvarphi}}\) is the difference vector and it gives the change in the mid-surface director, and \(\Psi\) and \(\gamma\) are components that are used to circumvent the spurious stresses that occur in the thickness direction of a six parameter formulation. The remaining theoretical development (e.g., derivation of the Green-Lagrange strain tensor, use of the principle of virtual displacement, and finite element model development) are not included here and the user is referred to Gutierrez Rivera et al. [10] for additional information.

2.3 A Numerical Example

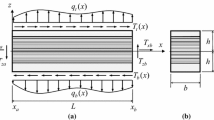
As a numerical example, we consider a simply supported isotropic cylindrical shell subjected to a non-displacement dependent internal pressure p (see Fig. 1). The results are compared with those presented by Amabili [1], where full non-linear terms associated with Green–Lagrange strain-displacement relations, third-order thickness stretch, and third-order shear deformation were used to describe the shell kinematics. The geometric parameters are L = 0.52 m, R = 0.15 m, and h = 0.03 m, and the load used is q = 12 GPa. It is assumed that the shell is made of stainless steel with material properties E = 198 GPa and \(\upsilon\) = 0.3. Symmetry is exploited and one octant of the shell is used as a computational domain. A uniform mesh of 4 × 4 with polynomial degree of 8 is used. The boundary conditions for the presented formulation are

Fig. 1
figure 1

Simply supported isotropic cylindrical shell with internal pressure

Full size image
$$x = 0,L:\quad u_{y} = u_{z} = \varphi_{y} = \varphi_{z} =\Psi = \gamma = 0$$
(2)

Figures 2 and 3 show, respectively, the normalized transverse displacement and thickness stretch versus the axial coordinate of the shell at point A. A very good agreement between the results obtained using the present formulation and the ones reported by Amabili [1] is observed. Figure 4 shows the deformed configuration for this isotropic shell at the maximum load q. As can be seen from Fig. 3, the thickness stretch is significant and it is the most near the constrained ends and uniform in the interior of the cylindrical shell.

Fig. 2
figure 2

Normalized transverse displacement versus normalized axial coordinate

Full size image
Fig. 3
figure 3

Normalized thickness stretch versus normalized axial coordinate

Full size image
Fig. 4
figure 4

Deformed configuration of the internally pressurized cylindrical shell

Full size image

3 Micropolar Plate Model for the Analysis of Web-Core Sandwich Plates

3.1 Background

Advances in manufacturing technologies have enabled the design and development of materials whose microstructure can be architected to achieve desired functionalities (see [7]). The scale of the architected microstructure can range from a few nanometers to several meters (see [3, 16]). Lattice materials used in sandwich panels are a class of architected materials whose microstructure is typically in the order of centimeters. Modelling of such plates accounting for the architectural details is computationally intensive. On the other hand, homogenization to reduce the sandwich plate to an equivalent single-layer plate will result in an inaccurate representation of the response. Therefore, model that is computationally inexpensive while accounting for the material behavior to the extent that the sandwich plate response is nearly the same as that would be obtained by 3D analysis. One such approach based on micropolar theory is presented here.

3.2 Formulation

The micropolar theory allows us to pass information on both displacements and rotations from the 3D unit cell into an equivalent single-layer plate model. The conventional shell finite elements used to model the 3D unit cell have both translational and rotational degrees of freedom that are related to the generalized displacement degrees of freedom of the micropolar FSDT plate theory. This way we are able to account, in addition to the antisymmetric shear deformations, for the local twisting and bending of the sandwich face sheets and webs with respect to their own mid-surfaces through couple-stress moments, which is not possible in a conventional FSDT sandwich plate theory. The two-scale approach based on energy equivalence between the 3D unit cell and the 2D micropolar plate provides the plate constitutive relations (see [11,12,13] for details).

3.2.1 Displacement Field of the Micropolar Plate Theory

The displacements and microrotations of a 2D shear deformable micropolar plate are

$$\begin{aligned} & U_{x} (x,y,z )= u_{x} (x,y )+ z\phi_{x} (x,y )\\ & U_{y} (x,y,z )= u_{y} (x,y,t )+ z\phi_{y} (x,y )\\ & U_{z} (x,y,z )= u_{z} (x,y )\\ & \varPsi_{x} (x,y,z )= \psi_{x} (x,y )\\ & \varPsi_{y} (x,y,z )= \psi_{y} (x,y )\\ & \varPsi_{z} (x,y,z )= 0\\ \end{aligned}$$
(3)

where \((u_{x} ,u_{y} ,u_{z} )\) denote the displacements of a point on the plane z = 0, and \((\phi_{x} ,\phi_{y} )\) are the rotations of a transverse normal about the y- and x-axes, respectively, whereas \((\psi_{x} ,\psi_{y} )\) are microrotations about the x- and y-axes, respectively. Note that \(\varPsi_{z} (x,y,z) = 0\) means that the micropolar plate theory for web-core sandwich panels will not have a drilling degree of freedom.

Following the theory of micropolar elasticity, the nonzero strains of the micropolar plate are obtained as follows:

$$\begin{aligned} & {\epsilon}_{\text{xx}} = u_{\text{x,x}} + {\text{z}}\phi_{\text{x,x}} = {\epsilon}_{\text{xx}}^{0} + {\text{z}}\kappa_{\text{xx}} \\ & {\epsilon}_{yy} = u_{\text{y,y}} + {\text{z}}\phi_{\text{y,y}} = {\epsilon}_{yy}^{0} + {\text{z}}\kappa_{\text{yy}} \\ & {\epsilon}_{xy} = u_{\text{y,x}} + {\text{z}}\phi_{\text{y,x}} = {\epsilon}_{\text{xy}}^{0} + {\text{z}}\kappa_{\text{xy}} \\ & {\epsilon}_{yx} = u_{\text{x,y}} + {\text{z}}\phi_{\text{x,y}} = {\epsilon}_{yx}^{0} + {\text{z}}\kappa_{yx} \\ & {\epsilon}_{xz} = u_{\text{z,x}} + \psi_{\text{y}} ,\,{\epsilon}_{\text{zx}} = \phi_{\text{x}} - \psi_{\text{y}} \\ & {\epsilon}_{yz} = u_{\text{z,y}} - \psi_{\text{x}} ,\,{\epsilon}_{\text{zy}} = \phi_{\text{y}} + \psi_{\text{x}} \\ & \chi_{\text{xx}} = \psi_{\text{x,x}} ,\,\chi_{\text{yy}} = \psi_{\text{y,y}} ,\,\chi_{\text{xy}} = \psi_{\text{y,x}} ,\,\chi_{\text{yx}} = \psi_{\text{x,y}} \\ \end{aligned}$$
(4)

3.2.2 Equations of the 2D Micropolar Plate Theory

Use of the principle of virtual displacements with appropriate expressions for the virtual strain energy potential associated with the micropolar plate theory and introduction of suitable stress resultants, we can derive the Euler equations associated with micropolar first-order shear deformation plate theory. For details, see Karttunen et al. [12]. The equations of motion of the 2D micropolar plate are:

$$\begin{array}{*{20}c} {N_{xx,x} + N_{xy,y} = 0,\,N_{yy,y} + N_{yx,x} = 0} \\ {M_{xx,x} + M_{xy,y} - Q_{x}^{s} + Q_{x}^{a} = 0} \\ {M_{yy,y} + M_{yx,x} - Q_{y}^{s} + Q_{y}^{a} = 0} \\ {Q_{x,x}^{s} + Q_{x,x}^{a} + Q_{y,y}^{s} + Q_{y,y}^{a} = - q} \\ {P_{yy,y} + P_{xy,x} - 2Q_{x}^{a} = 0,\,P_{xx,x} + P_{yx,y} + 2Q_{y}^{a} = 0} \\ \end{array}$$
(5)

where \((N_{xx} ,N_{yy} ,N_{xy} ,N_{yx} )\) are the in-plane membrane forces, \((M_{xx} ,M_{yy} ,M_{xy} ,M_{yx} )\) are the bending and twisting moments, \((Q_{x}^{a} ,Q_{y}^{a} )\) are antisymmetric shear forces, \((Q_{x}^{s} ,Q_{y}^{s} )\) symmetric shear forces, and \((P_{xx} ,P_{yy} ,P_{xy} )\) are the local (couple-stress related) bending and twisting resultants. The next step is to relate the plate degrees of freedom to the 3D unit cell displacement degrees of freedom.

3.2.3 Transformation Relations Between 3D Unit Cell and 2D Plate Theory

Figure 5 shows a web-core 3D unit cell attached to an arbitrary point of a micropolar plate; see the dashed line along z-axis. The 2D micropolar continuum plate as a whole is a macrostructure, and the 3D unit cell represents its periodic microstructure. In order to obtain the constitutive equations for the plate, the strain energy of the microscale FE unit cell is expressed in terms of the continuous macroscale displacement degrees of freedom so as to bridge the two scales.

Fig. 5
figure 5

Web-core 3D unit cell modeled by shell finite elements in Abaqus. The mesh is coarse for illustrative purposes. In generating a statically condensed FE model for the two-scale constitutive modeling approach, certain DOFs are retained on face edges A and B while all interior DOFs are condensed out. No boundary conditions are applied

Full size image

Static condensation is applied at all nodes of the FE unit cell in Fig. 5 to the rotation with respect to the z-axis. Certain nodal DOFs in the 3D unit cell are retained only at the highlighted face edge nodes of the unit cell. Ultimately, the nodal displacement degrees of freedom of the 3D unit cell are related to the nodal generalized displacement degrees of freedom of the plate theory, and the bridging of the two scales (i.e., 3D unit cell and the 2D plate) is founded on an assumption of strain energy equivalence between the macrostructure (plate) and the microstructure (3D unit cell); see Karttunen et al. [12] for details.

The explicit matrix form of the plate constitutive equations is given by

$$\left\{ {\begin{array}{*{20}c} {\text{N}} \\ {\text{M}} \\ {\text{Q}} \\ {\text{P}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\text{A}} & 0 & 0 & 0 \\ 0 & {\text{D}} & 0 & 0 \\ 0 & 0 & {\text{G}} & 0 \\ 0 & 0 & 0 & {\text{H}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\upvarepsilon^{0} } \\ \kappa \\ \gamma \\ \chi \\ \end{array} } \right\}$$
(6)

where N are the in-plane membrane forces, M are the bending and twisting moments, Q contains symmetric and antisymmetric shear forces, and P is the local (couple-stress related) bending and twisting resultants.

3.3 Numerical Example

A web-core unit cell made of steel with Young’s modulus E = 206 GPa, Poisson’s ratio ʋ = 0.3 and density ρ = 7850 kg/m3 is considered. The height of the unit cell is taken to be 0.044 m. The length and width of the unit cell are both taken to be l = 0.12 m so that the unit cell planform area is A = l2 = 0.0144 m2. The Navier solution for bending of the simply supported 2D micropolar plate under line load is obtained (see Fig. 5 for the plate geometry). A conventional plate under line load yields maximum displacement that is 34% for face sheet thicknesses of 2 mm compared to a 3D FE solution, whereas the 2D micropolar plate model gives only small error of 2.7% as it can emulate the 3D deformations better through non-classical antisymmetric shear behavior and local bending and twisting (see Fig. 6). The 3D FEM model consists of 60800 shell elements of S8R5 type from Abaqus, whereas the micropolar plate solution is obtained with a small fraction of the FEM solution.

Fig. 6
figure 6

a Transverse displacement of a 2-D micropolar web-core plate under a line load for tf = 4 mm. b Transverse displacement of the plate mid-section calculated by different models

Full size image

4 Conclusions

Beginning with a brief discussion of the author’s professional journey in mechanics, two of his recent research topics, namely, the development of a robust shell element and the modelling of web core sandwich plates are reviewed. The lecture will highlight various milestones of the author’s professional life.