Nonlinear Stability of Turbine and Generator Rotors Applying Hopf Bifurcation Theory

Abstract

The paper applies the Hopf bifurcation theory to assess the stability of turbine and generator rotor-bearing systems considering nonlinear bearing support models. Rotor systems may develop stable or unstable motions even when running at speeds lower than the threshold speed of instability. This case is examined in this paper when excitations may perturb the rotating system outside its stability envelope and when the potential for subcritical bifurcation exists. Two separate M-DOF rotor-bearing-foundation systems are used to represent a turbine rotor-bearing-foundation system and a generator rotor-bearing-foundation system. The rotor modelling considers the Transient Transfer Matrix Method, and the nonlinear lemon-bore bearings are modelled with direct solution of the Reynolds equation at the discrete time domain. Bearing pedestals are considered as lumped masses mounted in linear springs and dampers. The results highlight the need of considering nonlinear bearing models in the stability analysis of large rotor systems so as to avoid unstable operation at speeds lower than the threshold speed of instability, and to retain operation under certain excitations, e.g., seismic excitations.

1 Introduction

Turbine and generator rotors may suffer from instability while operating on site. This is a fact due to insufficient models, methods, and tools for predicting instability of such systems, and also due to unexpected extend of specific defects on the shaft train, e.g., misalignment. The stability assessment is a standard calculation on rotordynamic design evaluation of power generation shaft trains and linear models are used by most designers.

The prediction for stable operation in slender rotor systems (e.g., turbine-generator shaft trains) is based on the calculated logarithmic decrement of shaft modes and is still nowadays evaluated in standard design procedures with the computation of complex eigenvalues. The reader may advise the monumental work of Lund on the prediction of stability of rotor systems [1]. There are past and recent examples where marginal (and still acceptable according to standards) stability designs have rendered bearing oil-whirl instability on site operation of slender turbines. Marginal design regarding stability cannot be always avoided as the stability characteristics are strongly influenced by rotor slenderness which in some turbine modules (and generators) is relatively high (long and thin rotor). The case where stability is lost under subcritical Hopf bifurcation is the most dangerous. The shaft motion following a subcritical Hopf bifurcation may be bounded only by physical constraints, e.g., stator. Furthermore, the unstable motions are initiated at rotating speeds less than the linearly predicted threshold speed of instability. The special circumstances for a potential of subcritical Hopf bifurcation of turbine-generator rotor systems are discussed in this paper.

The Hopf bifurcation theory has been applied in the literature considering simple rotor systems. The reader should consider older [2,3,4] and recent works [5,6,7,8,9,10,11,12,13] on the relative objective, while a generic study of the theory and applications of Hopf bifurcations in mechanical systems can be found in [14, 15]. The recent papers of Wang and Khonsari [5,6,7,8,9,10] and of Miraskari et al. [12, 13] present a fundamental study on the prediction of supercritical and subcritical Hopf bifurcations in rotor systems with plain short bearings without foundation properties or bearing profile to be considered. The analytical formulas for the short bearing performance are proven very valuable for the application of Hopf theory in rotor-bearing systems as they offer analytical expressions for the first three derivatives of the forces with respect to displacement. However, in this paper the treatment of Hopf theory in rotor-bearing-foundation systems is entirely numerical because the journal bearings are considered of finite length and partial arc or lemon-bore profile. Furthermore, the algorithm for the prediction of instability threshold and bifurcation type (supercritical or subcritical) may consider M-DOF systems of complex rotors (e.g., turbine rotors). However, the results in this paper consider only 6 DOFs as the simple model of Jeffcott rotor is implemented and complex rotor systems of M-DOF are considered for future works.

The nonlinear bearing models consider partial arc or lemon-bore bearing profile of finite length, and they are evaluated at discrete time domain during the transient motion of the system. The lubrication performance considers laminar, isoviscous, and isothermal lubricant flow and the solution of the Reynolds equation is evaluated using the Finite Difference Method. The bearing models have been developed in past works of the author and are implemented on this paper so as to study realistic and widely applicable bearing profiles. The foundation properties are considered as linear springs and dampers mounting the lumped mass of the bearing pedestal. The results of the paper concern the prediction of stability threshold and the potential of supercritical or subcritical bifurcation on six different rotor classes in total, three for turbine configurations and three for generator rotors.

2 The Model of a Rotor-Bearing-Foundation System for Turbines and Generators

2.1 Rotor and Foundation Model

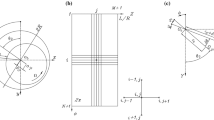
The model of the rotor-bearing-foundation system implements the Transient Transfer Matrix Method (TTMM) which enables the evaluation of nonlinear transient response. The unique source of nonlinearity in the system is the nonlinear fluid film forces in the bearings $F_{X}^{B}$ and $F_{Y}^{B}$. The method is explained in this section and in Appendix 1. The geometric and physical properties of the multiple rotor segments $N$ are discretized in $N + 1$ nodes carrying lumped masses, see Fig. 1a. The status vectors on the sides of each node ${\mathbf{Z}}_{i}^{L}$ and ${\mathbf{Z}}_{i}^{R}$, $i = 1,2, \ldots ,N + 1$, are time variant and the status are defined in Eq. (1), see also Fig. 1b. The displacements and the slopes on the sides of each lumped mass are equal, meaning that $y_{i}^{L} \left( t \right) = y_{i}^{R} \left( t \right) = y_{i} \left( t \right)$, $\theta_{Y,i}^{L} \left( t \right) = \theta_{Y,i}^{R} \left( t \right) = \theta_{Y,i} \left( t \right)$ and $x_{i}^{L} \left( t \right) = x_{i}^{R} \left( t \right) = x_{i} \left( t \right)$, $\theta_{X,i}^{L} \left( t \right) = \theta_{X,i}^{R} \left( t \right) = \theta_{X,i} \left( t \right)$. The entire analysis considers the coordinate system defined in Fig. 1b.

Fig. 1

a Multi-segment rotor as a lumped mass system. b The description of the fields and points that represent the segments and the nodes of the discretized system

$$\begin{aligned} {\mathbf{Z}}_{i}^{L} \left( t \right) = \left\{ {\begin{array}{*{20}c} {y_{i} \left( t \right)} & {\theta_{Y,i} \left( t \right)} & {M_{Y,i}^{L} \left( t \right)} & {V_{Y,i}^{L} \left( t \right)} & {x_{i} \left( t \right)} & {\theta_{X,i} \left( t \right)} & {M_{X,i}^{L} \left( t \right)} & {V_{X,i}^{L} \left( t \right)} & 1 \\ \end{array} } \right\}^{T} \hfill \\ {\mathbf{Z}}_{i}^{R} \left( t \right) = \left\{ {\begin{array}{*{20}c} {y_{i} \left( t \right)} & {\theta_{Y,i} \left( t \right)} & {M_{Y,i}^{R} \left( t \right)} & {V_{Y,i}^{R} \left( t \right)} & {x_{i} \left( t \right)} & {\theta_{X,i} \left( t \right)} & {M_{X,i}^{R} \left( t \right)} & {V_{X,i}^{R} \left( t \right)} & 1 \\ \end{array} } \right\}^{T} \hfill \\ \end{aligned}$$

(1)

The functions of the point matrix ${\mathbf{P}}_{i}$, field matrix ${\mathbf{F}}_{i}$, and transfer matrix ${\mathbf{T}}_{i}$, in Fig. 1b are described by the formulas ${\mathbf{Z}}_{i}^{L} \left( t \right) = {\mathbf{F}}_{i} \times {\mathbf{Z}}_{i - 1}^{R} \left( t \right)$, ${\mathbf{Z}}_{i}^{R} \left( t \right) = {\mathbf{P}}_{i} \times {\mathbf{Z}}_{i}^{L} \left( t \right)$ and ${\mathbf{T}}_{i} = {\mathbf{P}}_{i + 1} \times {\mathbf{F}}_{i}$. However, applying the Transient Transfer Matrix Method, there is no need to define the point matrix ${\mathbf{P}}_{i}$. The principle of the TTMM is based on that each nodal mass $M_{N,i}$ executes lateral and tilting transient motions (4 DoFs for each mass) under the effect of shearing and bending moment applied from the relative motions of the side nodal masses $M_{N,i - 1}$ and $M_{N,i + 1}$, see Fig. 2. Furthermore, the external forces acting to the mass $M_{N,i}$, such as unbalance, gravitational forces, and bearing impedance force, are incorporated. The 4-DoF equations of motion for the mass $M_{N,i}$ are given in Eq. (2).

Fig. 2

Definition of displacement and tilting angle of the nodal masses in two main planes, here a vertical, and b horizontal

$$\begin{array}{*{20}l} {M_{N,i} \cdot \ddot{x}_{i} = V_{X,i}^{R} - V_{X,i}^{L} + F_{X}^{B} + F_{X}^{U} } \hfill & {J_{ND,i} \cdot \ddot{\theta }_{X,i} = M_{X,i}^{R} - M_{X,i}^{L} - J_{NP,i} \cdot \Omega \cdot \dot{\theta }_{Y,i} } \hfill \\ {M_{N,i} \cdot \ddot{y}_{i} = V_{Y,i}^{R} - V_{Y,i}^{L} + F_{Y}^{B} + F_{Y}^{U} - F_{i}^{G} ,} \hfill & {J_{ND,i} \cdot \ddot{\theta }_{Y,i} = M_{Y,i}^{R} - M_{Y,i}^{L} + J_{NP,i} \cdot \Omega \cdot \dot{\theta }_{X,i} } \hfill \\ \end{array}$$

(2)

To evaluate the transient response of the system, the motion equations in Eq. (2) are integrated with a numerical technique, e.g., Runge-Kutta with variable time step for stiff systems if necessary, after the system is converted to an $8 \times 8$ system composed by 8 ODEs of first order. The correspondence of the state variables $q_{i}$ to the displacement and tilting angle of each mass is given in Eq. (3). Then, the motion equations for the lumped masses of the rotor are defined in Eq. (4).

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {x_{i} } & {\dot{x}_{i} } & {y_{i} } & {\dot{y}_{i} } & {\varphi_{X,i} } & {\dot{\varphi }_{X,i} } & {\varphi_{Y,i} } & {\dot{\varphi }_{Y,i} } \\ \end{array} } \right\}^{T} = \\ & \quad = \left\{ {\begin{array}{*{20}c} {q_{i} [1]} & {q_{i} [2]} & {q_{i} [3]} & {q_{i} [4]} & {q_{i} [5]} & {q_{i} [6]} & {q_{i} [7]} & {q_{i} [8]} \\ \end{array} } \right\}_{t}^{T} \\ \end{aligned}$$

(3)

$$\begin{array}{*{20}l} {\dot{q}_{i} [1] = q_{i} [2],} \hfill & {\dot{q}_{i} [5] = q_{i} [6]} \hfill \\ {\dot{q}_{i} [2] = \frac{1}{{M_{N,i} }}\left( {V_{X,i}^{R} - V_{X,i}^{L} + F_{X}^{B} + F_{X}^{U} } \right),} \hfill & {\dot{q}_{i} [6] = \frac{1}{{J_{ND,i} }}\left( {M_{X,i}^{R} - M_{X,i}^{L} - J_{NP,i} \cdot \Omega \cdot q_{i} [8]} \right)} \hfill \\ {\dot{q}_{i} [3] = q_{i} [4],} \hfill & {\dot{q}_{i} [7] = q_{i} [8]} \hfill \\ {\dot{q}_{i} [4] = \frac{1}{{M_{N,i} }}\left( {V_{Y,i}^{R} - V_{Y,i}^{L} + F_{Y}^{B} + F_{Y}^{U} - F_{i}^{G} } \right),} \hfill & {\dot{q}_{i} [8] = \frac{1}{{J_{ND,i} }}\left( {M_{Y,i}^{R} - M_{Y,i}^{L} + J_{NP,i} \cdot \Omega \cdot q_{i} [6]} \right)} \hfill \\ \end{array}$$

(4)

The system in Eq. (4) should be defined for every nodal mass, meaning for $i = 1,2, \ldots ,N + 1$ for a rotor with $N$ segments. Bearing forces $F_{X}^{B}$ and $F_{Y}^{B}$, and unbalance forces $F_{X}^{U}$ and $F_{Y}^{U}$ are introduced when in the respective node a bearing or unbalance exists, see Appendix 1. In Fig. 3, the translational motion of the pedestal mass may be described by a $2 \times 2$ system of 2 ODEs of second order in Eq. (5), where $x_{P}$ and $y_{P}$ is the absolute horizontal and vertical displacement of the pedestal. For a generic case that the foundation (ground) is exciated, e.g., by an earthquake, then $x_{S}$ and $y_{S}$ is the horizontal and vertical displacement of the foundation (ground) due to this excitation.

Fig. 3

Representation of the nonlinear bearing and the linear support structure (pedestal) as considered in the current model

$$\begin{aligned} M_{P,Y} \cdot \ddot{y}_{P} & = - K_{P,Y} \left( {y_{P} - y_{S} } \right) - C_{P,Y} \left( {\dot{y}_{P} - \dot{y}_{S} } \right) - F_{Y}^{B} - M_{P,Y} \cdot g \\ M_{P,X} \cdot \ddot{x}_{P} & = - K_{P,X} \left( {x_{P} - x_{S} } \right) - C_{P,X} \left( {\dot{x}_{P} - \dot{x}_{S} } \right) - F_{X}^{B} \\ \end{aligned}$$

(5)

In Eq. (5) the oil film forces $F_{X}^{B}$ and $F_{Y}^{B}$, and the foundation displacement excite the pedestal sub-system. However, in this paper there is no foundation excitation considered. With the definition of state variables in Eq. (6), the pedestal motion equations are converted to a $4 \times 4$ system of 4 ODEs of first order in Eq. (7). The oil film bearing forces couple the two systems of Eqs. (4) and (7) with the nonlinear oil film force model to account for the motion of the pedestal (bearing shell), see Fig. 3, and Sect. 2.2.

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {y_{P,j} } & {\dot{y}_{P,j} } & {x_{P,j} } & {\dot{x}_{P,j} } \\ \end{array} } \right\}^{T} = \\ & \quad = \left\{ {\begin{array}{*{20}c} {q_{j} [8\left( {N + 1} \right) + 1]} & {q_{j} [8\left( {N + 1} \right) + 2]} & {q_{j} [8\left( {N + 1} \right) + 3]} & {q_{j} [8\left( {N + 1} \right) + 4]} \\ \end{array} } \right\}_{t}^{T} \\ \end{aligned}$$

(6)

$$\begin{aligned} \dot{q}_{j} [8\left( {N + 1} \right) + 1] & = w_{j} [2] \\ \dot{q}_{j} [8\left( {N + 1} \right) + 2] & = - \frac{1}{{M_{P,Y} }}K_{P,Y} \left( {q_{j} [8\left( {N + 1} \right) + 1] - y_{P,0} - y_{S} } \right) \\ & \quad - \frac{1}{{M_{P,Y} }}\left( {C_{P,Y} \cdot \left( {q_{j} [8\left( {N + 1} \right) + 2] - \dot{y}_{S} } \right) + F_{Y}^{B} } \right) - g \\ \dot{q}_{j} [8\left( {N + 1} \right) + 3] & = w_{j} [4] \\ \dot{q}_{j} [8\left( {N + 1} \right) + 4] & = - \frac{1}{{M_{P,X} }}K_{P,Z} \cdot q_{j} [8\left( {N + 1} \right) + 3] \\ & \quad - \frac{1}{{M_{P,X} }}\left( {C_{P,X} \cdot \left( {q_{j} [8\left( {N + 1} \right) + 4] - \dot{x}_{S} } \right) + F_{X}^{B} } \right) \\ \end{aligned}$$

(7)

Each pedestal adds the respective equations of motion, meaning the Eqs. (6) and (7), $j = 1,2, \ldots ,{\text{NOB}}$, where NOB is the number of bearings. Therefore, a rotor with $N$ segments, and $N + 1$ nodal masses, mounted on NOB bearings will render $n = \left( {N + 1} \right) \cdot 8 + \left( {\text{NOB}} \right) \cdot 4$ equations of motion and respective unknowns, consisting a nonlinear autonomous system ${\dot{\mathbf{q}}} = {\mathbf{f}}\left( {{\mathbf{q}},\Omega } \right)$ when unbalance is absent, or a nonlinear non-autonomous system ${\dot{\mathbf{q}}} = {\mathbf{f}}\left( {{\mathbf{q}},\Omega ,t} \right)$ when unbalance is considered, see Appendix 1. The stability of the autonomous system ${\dot{\mathbf{q}}} = {\mathbf{f}}\left( {{\mathbf{q}},\Omega } \right)$ is assessed in Sect. 3 applying the Hopf bifurcation theory.

2.2 Model of Nonlinear Bearings

Most turbine and generator rotors of medium and high power (100–1000 MW) are mounted on lemon bore, partial arc, or other lobe bearing configuration. Non-synchronous turbine rotors of higher speeds (e.g., 4000 RPM, 5000 RPM, or higher) can be mounted on tilting-pad bearings, but there are many designs with large non-synchronous turbine rotors mounted on lobe bearings. These rotors can be coupled to the generator rotor through a gearbox. This is the example used in this paper, presented in Sect. 3.1.

A 2-lobe journal bearing (called also lemon-bore bearing, or elliptical bearing) is represented in Fig. 4. The bearing consists of two circular sectors of radius $R_{P}$; the upper sector is centred at $\left( {x_{P} , - y_{P} - y_{L} } \right)$, and the lower sector is centred at $\left( {x_{P} ,y_{P} + y_{L} } \right)$. The bearing centre $\left( {x_{P} ,y_{P} } \right)$ is represented by the coordinates for the bearing pedestal movement, $x_{P} ,y_{P}$, as described in previous section, see Fig. 3.

Fig. 4

Representation of the profile and of the key design parameters of a 2-lobe bearing (lemon-bore bearing)

The centre of each lobe does not coincide to the bearing centre, thus the bearing is said to be geometrically preloaded. Such a geometric configuration increases the journal bearing effective eccentricity and this is the principle behind the enhanced bearing stability of preloaded bearings [16,17,18,19,20]. The radius of the preloaded sectors is shown in Fig. 4 as $R_{P}$. The fluid film thickness h between the sliding surfaces of the journal and the bearing is well approximated from the formulas in Eq. (8) for the entire circumference $0 \le \theta \le 2\pi$, which can be expressed in dimensionless form as $H = h/c_{b}$. In Eq. (8), $x_{L} = 0$ because each lobe is not located at an offset relative to the bearing centre ($x_{L} \ne 0$ for offset lemon-bore bearings, known also as offset halves bearings).

$$h = H \cdot c_{b} = \left\{ \begin{aligned} & c_{p} - \left( {x_{j} - \left( {x_{L} + x_{P} } \right)} \right)\cos \left( \theta \right) - \left( {y_{j} - \left( {y_{L} + y_{P} } \right)} \right)\sin \left( \theta \right),\,{\text{lower}}\,{\text{pad}} \\ & c_{p} - \left( {x_{j} - \left( {x_{L} + x_{P} } \right)} \right)\cos \left( \theta \right) - \left( {y_{j} - \left( { - y_{L} - y_{P} } \right)} \right)\sin \left( \theta \right),{\text{upper}}\,{\text{pad}} \\ \end{aligned} \right.$$

(8)

The key design parameters in a lemon-bore bearing are the starting angle $\theta_{S}$ and the ending angle $\theta_{E}$ of the effective lubricating surface (bearing shell), the radial clearance (assembly clearance) defined as $c_{b} = R_{b} - R$, clearance $c_{p}$ (machined pad clearance) defined from the curvature $R_{p} = R + c_{p}$ at any of the two lobes, and the preload $m = 1 - c_{b} /c_{p}$ which influences intensively the threshold speed of instability and the respective bifurcation type. As a generic approach, the higher the preload is, the more stable the bearing is. Preload $m$ usually receives values at the range of $0.3 \le m \le 0.7$ in common applications. The bearing has a width $L_{b}$, and the lubricant is characterized by a dynamic viscosity μ which for simplicity is assumed constant in this paper (isoviscous flow of the lubricant). The journal rotates around its centre with a rotating speed Ω (spinning speed). Under dynamic conditions, the journal will perform whirling motion inside the bearing clearance, with velocities $\dot{x}_{j}$ and $\dot{y}_{j}$. The influence of the bearing profile in the stability of limit cycle motions of a rotor-bearing-foundation system has been widely studied in the literature. The lemon-bore bearing profile has been selected in this paper as it is widely applied in industrial turbomachinery of medium speed where slender rotors are included in the design (steam/gas turbines and generators).

The lubrication problem in this paper (evaluation of lubricant pressure distribution $p$ inside the bearing clearance for laminar isothermal flow) is defined by the Reynolds equation which includes all the previously defined geometric and physical parameters, see Eq. (9) [16]. Using Eq. (8), the right-hand side (RHS) of Eq. (9) is written after some math in Eq. (10) for the lower and upper pad, respectively. Setting dimensionless variables in Eq. (11), Eq. (9) is written in Eq. (12).

$$\frac{1}{{\mu R^{2} }}\frac{\partial }{\partial \theta }\left( {h^{3} \frac{\partial p}{\partial \theta }} \right) + \frac{{h^{3} }}{\mu }\frac{{\partial^{2} p}}{{\partial x^{2} }} = 6\Omega \frac{\partial h}{\partial \theta } + 12\frac{dh}{dt}$$

(9)

$${\text{RHS}} = \left\{ \begin{aligned} & \left( {6\,\Omega \,\left( {x_{j} - x_{P} } \right) - 12\left( {\dot{y}_{j} - \dot{y}_{P} } \right)} \right)\sin \left( \theta \right) \\ & \quad \quad \quad - \left( {6\,\Omega \,\left( {y_{j} - y_{P} - y_{L} } \right) + 12\left( {\dot{x}_{j} - \dot{x}_{P} } \right)} \right)\cos \left( \theta \right),\,\,\,{\text{lower pad}} \\ & \left( {6\,\Omega \,\left( {x_{j} - x_{P} } \right) - 12\left( {\dot{y}_{j} - \dot{y}_{P} } \right)} \right)\sin \left( \theta \right) \\ & \quad \quad \quad - \left( {6\,\Omega \,\left( {y_{j} - y_{P} + y_{L} } \right) + 12\left( {\dot{x}_{j} - \dot{x}_{P} } \right)} \right)\cos \left( \theta \right),\,\,\,{\text{upper pad}} \\ \end{aligned} \right.$$

(10)

$$\begin{aligned} & \bar{p} = \frac{{c_{b}^{2} p}}{{\mu \,\Omega R^{2} }},\,\varepsilon_{x} = \frac{{x_{j} - x_{P} }}{{c_{b} }},\varepsilon_{y} = \frac{{y_{j} - y_{P} }}{{c_{b} }},\varepsilon = \sqrt {\varepsilon_{x}^{2} + \varepsilon_{y}^{2} } \\ & \dot{\varepsilon }_{x} = \frac{{\dot{x}_{j} - \dot{x}_{P} }}{{c_{b} }},\dot{\varepsilon }_{y} = \frac{{\dot{y}_{j} - \dot{y}_{P} }}{{c_{b} }},\dot{\bar{\varepsilon }}_{x} = \frac{{\dot{\varepsilon }_{x} }}{\Omega },\,\dot{\bar{\varepsilon }}_{y} = \frac{{\dot{\varepsilon }_{y} }}{\Omega },\,k = \frac{2R}{{L_{b} }},\,\bar{x} = \frac{2x}{{L_{b} }},\dot{\varphi } = \,\frac{{\varepsilon_{x} \dot{\varepsilon }_{y} - \varepsilon_{y} \dot{\varepsilon }_{x} }}{{\varepsilon_{x}^{2} + \varepsilon_{y}^{2} }} \\ \end{aligned}$$

(11)

$$\frac{\partial }{\partial \theta }\left( {H^{3} \frac{{\partial \bar{p}}}{\partial \theta }} \right) + k^{2} H^{3} \frac{{\partial^{2} \bar{p}}}{{\partial \bar{x}^{2} }} = \left( {6\varepsilon_{x} - 12\dot{\bar{\varepsilon }}_{y} } \right)\sin \left( \theta \right) - \left( {6\varepsilon_{y} + 12\dot{\bar{\varepsilon }}_{x} } \right)\cos \left( \theta \right)$$

(12)

Reynolds equation (12) can be solved with the four variables $\varepsilon_{x}$, $\varepsilon_{y}$, $\dot{\bar{\varepsilon }}_{x}$, and $\dot{\bar{\varepsilon }}_{y}$ to receive specific values. The solution can be a numerical solution scheme, e.g., Finite Difference Method. Supposing that the FDM is implemented, with a definition of finite difference grid as $N_{x} \times N_{\theta }$, the respective intervals are defined as $\Delta x = L_{b} /N_{x}$ and $\Delta \theta = \left( {\theta_{E} - \theta_{S} } \right)/N_{\theta }$. The angles $\theta_{S}$ and $\theta_{E}$ can be any angles on the circumference if the corresponding fluid film functions have been defined, see Eq. (8). When pressure is evaluated, the resulting fluid film forces are given in dimensional form in Eq. (13).

$$\left\{ {\begin{array}{*{20}c} {F_{x}^{B} } \\ {F_{y}^{B} } \\ \end{array} } \right\} = \frac{{\mu \,\Omega R^{3} }}{{c_{b}^{2} }}\left\{ {\begin{array}{*{20}c} {\bar{F}_{x}^{B} } \\ {\bar{F}_{x}^{B} } \\ \end{array} } \right\} = \frac{{\mu \,\Omega R^{3} }}{{c_{b}^{2} }}\left\{ {\begin{array}{*{20}c} { - \mathop \sum \limits_{i = 1}^{{N_{x} }} \mathop \sum \limits_{j = 1}^{{N_{\theta } }} \left( {\Delta x \cdot \Delta \theta \cdot \bar{p}_{i,j} \cdot \cos \left( {\theta_{j} } \right)} \right)} \\ { - \mathop \sum \limits_{i = 1}^{{N_{x} }} \mathop \sum \limits_{j = 1}^{{N_{\theta } }} \left( {\Delta x \cdot \Delta \theta \cdot \bar{p}_{i,j} \cdot \sin \left( {\theta_{j} } \right)} \right)} \\ \end{array} } \right\}$$

(13)

For Gümbel boundary conditions, only $\bar{p}_{i,j} > 0$ values are implemented in the double sum in Eq. (13). Bearing forces $F_{x}^{B}$ and $F_{x}^{B}$ are requested at every discrete time interval during the numerical integration of the system ${\dot{\mathbf{q}}} = {\mathbf{f}}\left( {{\mathbf{q}},\Omega } \right)$.

3 Application of Hopf Bifurcation Theory in the Stability Assessment of Simple and Complex Rotor Systems

3.1 Supercritical and Subcritical Hopf Bifurcations in Simple Rotor-Bearing-Foundation Systems

A Jeffcott rotor mounted on nonlinear sliding bearings on resilient foundation is represented in Fig. 5 and is used in this section to depict the two different types of motion bifurcation that occurs when the rotating speed $\Omega$ is in the region of the threshold speed of instability $\Omega_{th}$.

Fig. 5

Representative layout of a Jeffcott rotor mounted on sliding bearings with resilient foundation

Assuming perfectly balanced rotors, the rotor-bearing-foundation system will develop stable or unstable oscillations depending on its design, the value of the rotating speed $\Omega$, and the initial conditions (or perturbations from equilibrium, e.g., seismic excitation). The nonlinear feature of the bearing forces introduces to the system the possibility to experience different types of instability. Unstable motions will definitely appear when $\Omega > \Omega_{th}$, but they can also appear when $\Omega < \Omega_{th}$ if certain conditions of the geometrical and physical properties of the system are satisfied; the study of these conditions is actually of major interest in this paper.

In Fig. 6 the threshold speed of instability of the Jeffcott rotor system is plotted as a function of bearing parameter $\varGamma$ and Sommerfeld number $S_{O}$, for various cases of rotor stiffness. In all cases presented there are two domains of subcritical bifurcation, and one domain of supercritical bifurcation. In Fig. 6a there are four operational points indicated in the chart by two squares and two rhombuses. The squares correspond to operating speeds lower than the threshold speed of instability, while the rhombuses correspond to speeds higher than the threshold speed. These four cases of operation are selected to indicate how the system motion progresses. The respective transient motions are evaluated and plotted in Figs. 7 and 8.

Fig. 6

Instability threshold speed $\bar{\Omega }_{th}$ and type of bifurcation as function of a parameter $\varGamma$ and b Sommerfeld number $S_{O}$, for various cases of dimensionless rotor stiffness $\bar{K}$ and rigid foundation

Fig. 7

Journal orbits in supercritical bifurcation; no unbalance is considered. a Asymptotically stable motion when $\bar{\Omega } < \bar{\Omega }_{th}$, not depended on the initial conditions; b orbital asymptotically stable motion when $\bar{\Omega } > \bar{\Omega }_{th}$, and initial conditions out of the stability envelope (limit cycle); c orbital asymptotically stable motion when $\bar{\Omega } > \bar{\Omega }_{th}$, and initial conditions inside the stability envelope (limit cycle)

Fig. 8

Journal orbits in subcritical bifurcation; no unbalance is considered. a Asymptotically stable motion when $\bar{\Omega } < \bar{\Omega }_{th}$, and initial conditions within the stability envelope (limit cycle), b unstable motion when $\bar{\Omega } < \bar{\Omega }_{th}$, and initial conditions out of the stability envelope (limit cycle), c unstable motion when $\bar{\Omega } > \bar{\Omega }_{th}$, not depended on the initial conditions

In Fig. 7, transient motions of the rotor system are depicted during a supercritical Hopf bifurcation. In Fig. 7a it is shown that a perfectly balanced rotor will be asymptotically stable when the operating speed is lower than the threshold speed of instability. This occurs for any initial condition if the operating parameter $\varGamma$ corresponds to supercritical bifurcation (black square in Fig. 6a). Increasing the operating speed higher than the threshold speed of instability (black rhombus in Fig. 6a), the system motion is orbitally asymptotically stable. This means that when the initial condition is outside the limit cycle (stability envelope), see Fig. 7b, the rotor transient motion is asymptotical to the limit cycle, approaching from the outer side. When the initial condition is inside the limit cycle (stability envelope), then the rotor transient motion is asymptotical to the limit cycle from the inner side.

At the case that the parameter $\varGamma$ corresponds to subcritical bifurcation (white square in Fig. 6a), stable motion occurs at operating speeds lower than threshold speed of instability (white square in Fig. 6a), if the initial condition is inside the limit cycle (stability envelope). The motion is said to be asymptotically stable, see Fig. 8a. If the initial condition is outside the limit cycle (stability envelope), then the motion is unstable and with the progress of time it will be bounded only by physical constraints. At this case the journal motion approaches the bearing clearance, see Fig. 8b. Unstable motions will be occurring regardless the initial condition, when operating speed is higher than threshold speed, and parameter $\varGamma$ corresponds to subcritical bifurcation (white rhombus in Fig. 6a). This case is depicted in Fig. 8c.

Similar motions to those evaluated for the simple rotor system in this section are evaluated in the next section for full rotor-bearing-foundation systems of realistic applications.

It has to be clarified that in this paper only Hopf bifurcations are supposed to occur in the slender rotor-bearing-foundation systems studied. The systems studied in this paper will present at most cases a complex conjugate pair of eigenvalues crossing the imaginary axis as the rotor speed increases as they represent slender medium speed systems (1000–10,000 RPM) in terms of rotor flexibility, bearing properties, and foundation properties (steam/gas turbine rotors and generator rotors). Such systems will hardly demonstrate overdamped modes which would render real eigenvalues. The damping factor ($\zeta$) in most applications of such systems does not exceed $\zeta = 0.8$ corresponding to a logarithmic decrement lower than $\delta = 5$. However, in a generic theoretical basis other more complex motions are possible in other rotor systems, e.g., quasi-periodic or chaotic motions are possible especially in high speed systems. Such motions cannot be captured with the methodology employed in this paper. For the qualitative analysis of nonlinear systems able to produce any kind of motion, the reader may consider [21, 22] among others, where eigenvalues are not always considered complex quantities. More specifically, for the study of complex motions in nonlinear rotor-bearing systems, the reader may consider [23,24,25] where geared systems in nonlinear oil film bearings are investigated, together with [26, 27].

The stability assessment presented in this section considers the stability of one of the solutions checked, and it is assumed that a stable solution renders a stable system. Therefore, the statement that the system is stable implies that one of the solutions checked is stable. This solution is the one corresponding to the equilibrium of the perfectly balanced rotor inside the bearing clearance. However, more solutions may exist, like the limit cycle when supercritical bifurcation occurs, whose stability is assessed in this paper so as to identify whether the system is orbitally asymptotically stable; again, it is matter of whether the solution is stable or not.

3.2 Supercritical and Subcritical Hopf Bifurcations in Turbine and Generator Rotor Systems

This stability threshold and the respective type of Hopf bifurcation is evaluated in this section for indicative designs of turbine and generator rotors which cover the some applications of turbine-generator shaft trains for power generation, in regard to key design parameters like rotor slenderness ratio $\lambda$, bearing length to diameter ratio $L_{b} /D_{b}$, and foundation (pedestal) properties. In order to assess the stability of real rotors, a representative shaft train depicted in Fig. 9a is used. The Generator rotor is coupled to the Turbine rotor through a Gearbox and flexible couplings.

Fig. 9

a Representative configuration of a Turbine Rotor coupled through flexible coupling to Gearbox and Generator; 4 bearings are considered. Representative outline of b a generator shaft and c a turbine shaft. In (b) and (c), hatched area $A_{S}$ indicates stiffness diameters considered in the definition of slenderness ratio $\lambda = L/D_{eq} = L^{2} /A_{s}$

The flexural vibrations of the turbine and generator rotor do not influence each other as the couplings bending stiffness is low enough compared the rotor stiffness. This is not the case for torsional vibrations though. Three Generator rotors and three turbine rotors are assessed in this section regarding their stability characteristics. The six different rotor classes are defined through the slenderness ratio $\lambda$, here defined as $\lambda = L^{2} /A_{S}$ both for Generator rotors, see Fig. 9b, and Turbine Rotors, see Fig. 9c. Figure 9b and c represent indicative designs of generator and Turbine rotors, respectively; the hatched area $A_{S}$ depicts the diameter of each rotor cross section in which bending stresses are supposed to be developed; this is simply called ‘‘stiffness diameter’’. The bearing span is defined by $L$. An equivalent diameter $D_{eq}$ is also depicted in both rotors, representing the diameter of a uniform rotor of length $L$ and slenderness ratio $\lambda$. The higher the slenderness ratio is, the lower the effective bending stiffness $K_{S}$ of the rotor is.

The values of $\lambda$ checked in this section are shown in Table 1 together with the respective dimensionless stiffness $\bar{K}$ of the rotor and the dimensionless bearing parameter $\varGamma$, with both bearings of each rotor to be included. Driven end bearing “DE” is the bearing located in the coupled side of the rotor. Non-driven end bearing “NDE” is the bearing at the free (uncoupled) side of the rotor. In real applications, it is not uncommon that the slenderness ratio of turbine rotors may exceed the values included in Table 1, e.g., receiving values of 10 or 11, or higher, depending on how they are coupled to other rotors. This section considers Turbine rotors which are not part of turbine shaft trains. There are many configurations and layouts of turbine rotors in shaft trains and the nonlinear stability assessment can be cumbersome as the degrees of freedom increase.

Table 1 Properties of the turbine and generator rotors. DE: Driven End bearing, NDE: Non-Driven End bearing

The bearing length to diameter ratio is presented in Table 2 for the respective rotor classes. Each bearing pedestal is simulated as a rigid body of lumped mass $M_{P,Y}$ and $M_{P,X}$ in vertical and horizontal direction which is connected to the ground through springs of stiffness $K_{P,Y}$ and $K_{P,X}$, and dampers $C_{P,Y}$ and $C_{P,X}$ as in Fig. 3. Stiffness and damping for the pedestal structure do not depend on frequency of excitation (rotating speed) in the applications of this paper. However, the oil film impedance forces $F_{X}^{B}$ and $F_{Y}^{B}$ (see Fig. 3), applied from the oil film to the pedestal and the rotor, are nonlinear functions of the displacement and velocity of the respective journal and pedestal. The indicative values for the pedestal properties for the various rotors tested in this paper are included in Table 3.

Table 2 Bearing geometric properties. DE: Driven End bearing, NDE: Non-Driven End bearing

Table 3 Bearing pedestal physical properties. DE: Driven End bearing, NDE: Non-Driven End bearing

The dynamic response of each rotor is evaluated as presented in Sects. 2.1 and 2.2 using the Transient Transfer Matrix Method—TTMM, see also Appendix 1. The Hopf bifurcation theory is applied in the system ${\dot{\mathbf{q}}} = {\mathbf{f}}\left( {{\mathbf{q}},\Omega } \right)$ composed in Sect. 2.1, defined here for the six turbine/generator rotor-bearing-pedestal systems as described above. The dynamic viscosity $\mu$ of the lubricant is equal at both bearings mounting the rotor and is theoretically varying to change parameter $\varGamma$ of the bearings; this is how the charts of Figs. 10 and 11 are constructed.

Fig. 10

Instability threshold speed $\bar{\Omega }_{th}$ and type of bifurcation as function of parameter $\varGamma$

Fig. 11

Instability threshold speed $\bar{\Omega }_{th}$ and type of bifurcation as function of Sommerfeld number $S_{o}$

There are two lines in each chart of Figs. 10 and 11, line ‘‘1’’, and line ‘‘2’’. These correspond to the two different bearings. The geometrical properties of each bearing are used to define the non-dimensional parameter $\varGamma$, therefore, the parameters $\varGamma_{1}$ and $\varGamma_{2}$ are defined. The same goes for Sommerfeld number $S_{o}$ whose values are calculated for each bearing as $S_{o,1}$ and $S_{o,2}$ in the charts of Fig. 11. The charts of Fig. 10 are constructed for selected values of $\varGamma_{1}$. The dynamic viscosity, which is equal at both bearings, is calculated next. The values of $\varGamma_{2}$, $S_{o,1}$, and $S_{o,2}$ are then calculated. It is important to highlight that the bearing parameter $\varGamma$ is not speed depended.

In Fig. 10 the threshold speed of instability $\bar{\Omega }_{th,1} = \Omega_{th} \sqrt {c_{b,1} /g}$ is plotted as a function of bearing parameter $\varGamma_{1} = \mu \cdot R_{b,1} \cdot L_{b,1} \cdot M^{ - 1} \cdot c_{b,1}^{ - 2.5} \cdot g^{ - 0.5}$ in line ‘‘1’’. At the same charts, the threshold speed of instability $\bar{\Omega }_{th,2} = \Omega_{th} \sqrt {c_{b,2} /g}$ is plotted as a function of bearing parameter $\varGamma_{2} = \mu \cdot R_{b,2} \cdot L_{b,2} \cdot M^{ - 1} \cdot c_{b,2}^{ - 2.5} \cdot g^{ - 0.5}$ in line ‘‘2’’. The corresponding charts in Fig. 11 consider the Sommerfeld number at the first bearing $S_{o,1} = \mu R_{b,1} L_{b,1} \Omega_{th} \cdot \left( {2\pi } \right)^{ - 1} \cdot \left( {R_{b,1} /c_{b,1} } \right)^{2} \cdot \left( {Mg/2} \right)^{ - 1}$ and at the second bearing $S_{o,2} = \mu R_{b,2} L_{b,2} \Omega_{th} \cdot \left( {2\pi } \right)^{ - 1} \cdot \left( {R_{b,2} /c_{b,2} } \right)^{2} \cdot \left( {Mg/2} \right)^{ - 1}$, see also Fig. 9b, c for the definitions of first and second bearing.

Figure 10a, b, and c depict the bearing design parameter $\varGamma$ which render subcritical or supercritical bifurcation in the turbine rotor systems of Rotor Class 1, Rotor Class 2, and Rotor Class 3, respectively, see also Tables 1, 2, and 3 for the corresponding geometric and physical properties of the systems. Supercritical and subcritical bifurcation is denoted for the bearing design parameter $\varGamma$ of generator rotor systems in Fig. 10d, e, and f, which correspond to Rotor Class 4, 5, and 6. İt is worth noting that Rotor Class 5 generator, see Fig. 10e, has a very narrow range of $\varGamma$ parameter for which subcritical bifurcation can be developed.

As a generic comment, the subcritical bifurcation may occur in a wider range of parameter $\varGamma$. However, for real systems, the parameter $\varGamma$ would lie approximately in the range from 0.1 to 1. Regarding Fig. 11, the Sommerfeld number in real systems would lie approximately on the range from 0.2 to 0.7. According to Figs. 10 and 11, it is very likely that turbine and generator rotors have the potential for subcritical bifurcation, which as discussed in Sect. 3.1 may have catastrophic consequences.

The design engineer may predict the potential for supercritical or subcritical bifurcation of turbine-generator rotor systems with the calculation of the respective charts in Figs. 10 and 11. A design of a slender rotor should avoid the subcritical bifurcation as this may initiate instability at speeds lower than the threshold, see Sect. 3.1.

The frequency $\omega_{0}$ of the limit cycle motion when bifurcation occurs is predicted from the Hopf bifurcation theory in Appendix 2, see definition $\omega_{0} = {\mathbf{J}}_{\text{Y}} \left( 0 \right)[2,1]$ in Eq. (24).

This is calculated for the various cases of parameter $\varGamma$ and for the six Rotor Classes, and depicted in Fig. 12 divided by the rotor’s speed $\Omega_{th}$ when bifurcation occurs. Figure 12 depicts that there is a considerable change on the whirl frequency of the rotor when bifurcation occurs, depending on the rotor and bearing design, and this frequency is not always close to 50% of the rotating speed, but it may take values of 20% or even 15% of the rotating speed when the rotor is slender and the bearings heavy loaded (low Sommerfeld number). As mentioned above the Sommerfeld number in real applications of turbines and generators takes values at the range of 0.2–0.7, therefore, limit cycle motions of frequency higher than 20% of rotating speed should be expected in the case of supercritical bifurcation. Different bearing profiles, e.g., partial arc bearings of lower arc length may render even lower $\omega_{0} /\Omega_{th}$ ratio. This is the reason that when long generators enter oilf whirl instability, there are frequency components around 15–25% of synchronous frequency.

Fig. 12

Ratio of frequency of limit cycle motion to rotor speed $\omega_{0} /\Omega_{th}$, as a function of a parameter $\varGamma$, and b Sommerfeld number $S_{o}$ at one of the bearings

4 Conclusions

Realistic configurations of turbine and generator rotors were tested through full models of rotor-bearing-foundation systems, on the potential to develop supercritical and subcritical Hopf bifurcations. A short application of Hopf bifurcation theory in a simple rotor system was also included, depicting the transient motions of the rotor system when a Hopf bifurcation occurs. The following conclusions may be considered from rotordynamic engineers on turbine-generator designs.

The bearing design parameters such as profile configuration, clearance, length, diameter, dynamic viscosity, load, and speed have major influence on the potential of the rotor system to generate subcritical or supercritical bifurcations. A design which can render supercritical bifurcation is safer compared to the design that can render subcritical bifurcation. At the first case the limit cycle motions may have certain extend and the operation may be retained, while at the second case the rotor motions are bounded only from physical constraints (e.g., rotor-stator contact). A rotor system with the potential of subcritical bifurcation may lose stability in rotating speeds lower than the threshold speed of instability predicted by the linear stability assessment when certain perturbations take place, e.g., seismic excitation, high unbalance, or rub.

For the lemon-bore bearing profile tested, and for the rotor configuration tested, it was found that subcritical bifurcations are very likely to occur in realistic rotor systems of turbines and generators.

The frequency of limit cycle motion when supercritical bifurcation occurs varies according to the rotor and bearing design parameters. Slender rotors mounted on high loaded bearings tend to whirl with lower frequencies when bifurcation occurs. At this case, the whirl speed ratio is expected at the range from 15 to 25%. However, the whirl speed ratio of short rotors mounted on lightly loaded bearings should be expected close to 50%.

Appendix

1.1 Appendix 1. Modelling of the Rotor Using the Transient Transfer Matrix Method

The status vectors ${\mathbf{Z}}_{i}^{L}$ and ${\mathbf{Z}}_{i}^{R}$ are split in two vectors each, corresponding to the displacement/tilting and to the moments/forces as in Eq. (14).

$$\begin{aligned} {\mathbf{Z}}_{D,i} \left( t \right) = \left\{ {\begin{array}{*{20}c} {y_{i} \left( t \right)} & {\theta_{Y,i} \left( t \right)} & { - x_{i} \left( t \right)} & {\theta_{X,i} \left( t \right)} \\ \end{array} } \right\}^{T} \hfill \\ {\mathbf{Z}}_{F,i}^{R} \left( t \right) = \left\{ {\begin{array}{*{20}c} {M_{Y,i}^{R} \left( t \right)} & {V_{X,i}^{R} \left( t \right)} & {M_{X,i}^{R} \left( t \right)} & { - V_{Y,i}^{R} \left( t \right)} \\ \end{array} } \right\}^{T} \hfill \\ {\mathbf{Z}}_{F,i}^{L} \left( t \right) = \left\{ {\begin{array}{*{20}c} {M_{Y,i}^{L} \left( t \right)} & {V_{X,i}^{L} \left( t \right)} & {M_{X,i}^{L} \left( t \right)} & { - V_{Y,i}^{L} \left( t \right)} \\ \end{array} } \right\}^{T} \hfill \\ \end{aligned}$$

(14)

The moments/forces acting at the left and right of the mass $M_{N,i}$ are defined as ${\mathbf{Z}}_{F,i}^{L} \left( t \right)$ and ${\mathbf{Z}}_{F,i}^{R} \left( t \right)$, respectively. In this way, the expression ${\mathbf{Z}}_{i}^{L} \left( t \right) = {\mathbf{F}}_{i} \times {\mathbf{Z}}_{i - 1}^{R} \left( t \right)$ may be converted to the expression in Eq. (15) including the definitions of Eq. (14). The submatrices ${\mathbf{F}}_{DD,i}$, ${\mathbf{F}}_{DF,i}$, ${\mathbf{F}}_{FD,i}$, and ${\mathbf{F}}_{FF,i}$ are defined in Eq. (16).

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{Z}}_{D,i} \left( t \right)} \\ {{\mathbf{Z}}_{F,i}^{L} \left( t \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{DD,i} } & {{\mathbf{F}}_{DF,i} } \\ {{\mathbf{F}}_{FD,i} } & {{\mathbf{F}}_{FF,i} } \\ \end{array} } \right] \times \left\{ {\begin{array}{*{20}c} {{\mathbf{Z}}_{D,i - 1} \left( t \right)} \\ {{\mathbf{Z}}_{F,i - 1}^{R} \left( t \right)} \\ \end{array} } \right\}$$

(15)

$${\mathbf{F}}_{DD,i} = \left[ {\begin{array}{*{20}c} 1 & {L_{S,i} } & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {L_{S,i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],{\text{F}}_{FD,i} = \left[ 0 \right]_{{\left( {4 \times 4} \right)}} ,{\text{F}}_{FF,i} = \left[ {\begin{array}{*{20}c} 1 & { - L_{S,i} } & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & { - L_{S,i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

$${\mathbf{F}}_{DF,i} = \left[ {\begin{array}{*{20}c} {\frac{{L_{S,i}^{2} }}{{2E_{i} I_{S,i} }}} & { - \frac{{L_{S,i}^{3} }}{{6E_{i} I_{S,i} }} + \frac{{sf_{i} L_{S,i} }}{{G_{i} A_{S,i} }}} & 0 & 0 \\ {\frac{{L_{S,i} }}{{E_{i} I_{S,i} }}} & { - \frac{{L_{S,i}^{2} }}{{2E_{i} I_{S,i} }}} & 0 & 0 \\ 0 & 0 & {\frac{{L_{S,i}^{2} }}{{2E_{i} I_{S,i} }}} & { - \frac{{L_{S,i}^{3} }}{{6E_{i} I_{S,i} }} + \frac{{sf_{i} L_{S,i} }}{{G_{i} A_{S,i} }}} \\ 0 & 0 & {\frac{{L_{S,i} }}{{E_{i} I_{S,i} }}} & { - \frac{{L_{S,i}^{2} }}{{2E_{i} I_{S,i} }}} \\ \end{array} } \right]$$

(16)

Equation (15) is expressed as a system of two equations with unknowns the force/moment vectors ${\mathbf{Z}}_{F,i}^{L} \left( t \right)$ and ${\mathbf{Z}}_{F,i - 1}^{R} \left( t \right)$ and its solution is defined in Eqs. (17) and (18).

$${\mathbf{Z}}_{F,i - 1}^{R} \left( t \right) = {\mathbf{F}}_{DF,i}^{ - 1} \times \left( {{\mathbf{Z}}_{D,i} \left( t \right) - {\mathbf{F}}_{DD,i} \times {\mathbf{Z}}_{D,i - 1} \left( t \right)} \right)$$

(17)

$${\mathbf{Z}}_{F,i}^{L} \left( t \right) = {\mathbf{F}}_{FD,i} \times {\mathbf{Z}}_{D,i - 1} \left( t \right) + {\mathbf{F}}_{FF,i} \times \left( {{\mathbf{F}}_{DF,i}^{ - 1} \times \left( {{\mathbf{Z}}_{D,i} \left( t \right) - {\mathbf{F}}_{DD,i} \times {\mathbf{Z}}_{D,i - 1} \left( t \right)} \right)} \right)$$

(18)

Equations (17) and (18) express that if the displacement vectors are known in all nodes, then the force vectors can be evaluated in all nodes. The force vectors will be the input for the definition of motion equations of each mass in Eq. (4). Note that Eqs. (17) and (18) can be written for $i = 2,3, \ldots ,N + 1$. Then, for an initial condition for every ${\mathbf{Z}}_{D,i}$, and for $i = 1,2, \ldots ,N + 1$, the resulting bending moment and shearing force on the left and on the right side of each node $i$ will be given from Eqs. (17) and (18), excluding the values for the left of the first node ${\mathbf{Z}}_{F,1}^{L}$ and for the right of the last node ${\mathbf{Z}}_{F,N + 1}^{R}$. These should be set equal to zero since they correspond to free-end boundary conditions, meaning that ${\mathbf{Z}}_{F,1}^{L} = {\mathbf{Z}}_{F,N + 1}^{R} = \left\{ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} } \right\}^{T}$. Should a different boundary condition be applied, the corresponding vectors are defined for ${\mathbf{Z}}_{F,1}^{L}$ and ${\mathbf{Z}}_{F,N + 1}^{R}$.

$$\begin{aligned} \begin{array}{*{20}l} \begin{aligned} M_{X,i}^{L} \left( t \right) = {\mathbf{Z}}_{F,i}^{L} [3] \hfill \\ M_{Y,i}^{L} \left( t \right) = {\mathbf{Z}}_{F,i}^{L} [1], \hfill \\ \end{aligned} \hfill & \begin{aligned} V_{X,i}^{L} \left( t \right) = {\mathbf{Z}}_{F,i}^{L} [2] \hfill \\ V_{Y,i}^{L} \left( t \right) = - {\mathbf{Z}}_{F,i}^{L} [4], \hfill \\ \end{aligned} \hfill & \begin{aligned} M_{X,i}^{R} \left( t \right) = {\mathbf{Z}}_{F,i}^{R} [3] \hfill \\ M_{Y,i}^{R} \left( t \right) = {\mathbf{Z}}_{F,i}^{R} [1], \hfill \\ \end{aligned} \hfill & \begin{aligned} V_{X,i}^{R} \left( t \right) = {\mathbf{Z}}_{F,i}^{R} [2] \hfill \\ V_{Y,i}^{R} \left( t \right) = - {\mathbf{Z}}_{F,i}^{R} [4] \hfill \\ \end{aligned} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ \end{array} \hfill \\ \hfill \\ \end{aligned}$$

(19)

When unbalance force acts at a node this is defined in vertical and horizontal direction in Eq. (20) for constant rotating speed $\Omega$, and in Eq. (21) for linearly varying rotating speed (run-up/down) $\Omega = a \cdot t$ (where $a = \dot{\Omega }$), where $U$ is the unbalance magnitude.

$$F_{Y}^{U} = U \cdot \Omega^{2} \cdot \cos \left( {\Omega \cdot t} \right),F_{X}^{U} = - U \cdot \Omega^{2} \cdot \sin \left( {\Omega \cdot t} \right)$$

(20)

$$F_{Y}^{U} = U \cdot \Omega^{2} \cdot \cos \left( {0.5\,a \cdot t^{2} } \right),F_{X}^{U} = - U \cdot \Omega^{2} \cdot \sin \left( {0.5\,a \cdot t^{2} } \right)$$

(21)

Motion equations should also consider the gravitational force acting at each mass $M_{N,i}$ of the rotor, given as $F_{i}^{G} = M_{N,i} \cdot g$.

1.2 Appendix 2. Formulas for the Application of Hopf Bifurcation Theory

The evaluation of response at a limit cycle of a nonlinear autonomous system of the form ${\dot{\mathbf{q}}} = {\mathbf{f}}({\mathbf{q}},\Omega )$ is given in this section according to [15]. The size of the system is $n \times n$, and the bifurcation parameter is $\Omega$.

At first, the equilibrium points of the system ${\mathbf{q}}_{{\mathbf{*}}} \left( \Omega \right)$ (critical points) have to be evaluated for the different values of $\Omega$, using a numerical method, e.g., Newton-Raphson. For each critical point, the Jacobian matrix ${\mathbf{J}}$ (see Eq. 22) and its eigenvalues and eigenvectors have to be evaluated simultaneously; the eigenvalues should be ordered as ${\text{real}}\left( {\lambda_{1,2} } \right) > {\text{real}}\left( {\lambda_{3,4} } \right) >$${\text{real}}\left( {\lambda_{5,6} } \right) > \ldots$$> {\text{real}}\left( {\lambda_{n - 1,n} } \right)$; the eigenvectors ${\varvec{\upnu}}_{{j,\left( {n \times 1} \right)}}$ are placed correspondingly to this sequence of eigenvalues too. The interest is to find the $\Omega_{th}$ for which the eigenvalues of ${\mathbf{J}}\left( {\Omega_{th} } \right)$ contain a pair $\lambda_{1,2} = {\text{a}}\left( {\Omega_{th} } \right) \pm {\text{i}}\,{\text{b}}\left( {\Omega_{th} } \right)$ where ${\text{real}}\left( {\lambda_{1,2} } \right) = {\text{a}}\left( {{\Omega }_{th} } \right) = 0$.

$${\mathbf{J}}\left( {\Omega_{th} } \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1} }}{{\partial x_{1} }}} & {\frac{{\partial f_{1} }}{{\partial x_{2} }}} & \ldots & {\frac{{\partial f_{1} }}{{\partial x_{n} }}} \\ {\frac{{\partial f_{2} }}{{\partial x_{1} }}} & {\frac{{\partial f_{2} }}{{\partial x_{2} }}} & \ldots & {\frac{{\partial f_{2} }}{{\partial x_{n} }}} \\ \vdots & \vdots & \ldots & \vdots \\ {\frac{{\partial f_{n} }}{{\partial x_{1} }}} & {\frac{{\partial f_{n} }}{{\partial x_{2} }}} & \ldots & {\frac{{\partial f_{n} }}{{\partial x_{n} }}} \\ \end{array} } \right]_{{\Omega = \Omega_{th} }}$$

(22)

The reader has to check whether ${\text{real}}\left( {\lambda^{\prime}_{1} \left( {\Omega_{th} } \right)} \right) = {\text{real}}\left( {\left. {\frac{{\partial \lambda_{1} }}{\partial \Omega }} \right|_{{{\Omega } = {\Omega }_{th} }} } \right) = {\text{a}}^{\prime}\left( {\Omega_{th} } \right)$ and ${\text{b}}\left( {\Omega_{th} } \right)$ are non-zero quantities, and ${\text{real}}\left( {\lambda_{k} } \right) < 0$ for $k = 3,4, \ldots n$. If the above are satisfied, then the system undergoes a Hopf bifurcation as $\Omega$ crosses $\Omega_{th}$.

The matrix ${\mathbf{P}}_{n \times n}$ is formed in Eq. (24) using the eigenvectors of ${\mathbf{J}}\left( {\Omega_{th} } \right)$. The eigenvectors in ${\mathbf{P}}_{n \times n}$ have to be normalized so that the first element of the first vector to be 1. For MATLAB users, this can be achieved just by dividing all eigenvectors yielded by the command ‘‘$\left[ {V, \, D} \right] \, = {\text{ eig}}\left( {\mathbf{J}} \right)$” by the first element of ${\varvec{\upnu}}_{1}$, ${\varvec{\upnu}}_{1} [1]$.

$${\mathbf{P}}_{n \times n} = \frac{1}{{{\mathbf{v}}_{{\mathbf{1}}} \left[ 1 \right]}}\left[ {\begin{array}{*{20}c} {{\text{real}}\left( {{\varvec{\upnu}}_{{1,\left( {n \times 1} \right)}} } \right)} & { - {\text{imag}}\left( {{\varvec{\upnu}}_{{2,\left( {n \times 1} \right)}} } \right)} & {\begin{array}{*{20}c} {{\varvec{\upnu}}_{{3,\left( {n \times 1} \right)}} } & \cdots & {{\varvec{\upnu}}_{{n,\left( {n \times 1} \right)}} } \\ \end{array} } \\ \end{array} } \right]$$

(23)

The change of variables ${\mathbf{q}} = {\mathbf{q}}_{{\mathbf{*}}} + {\mathbf{P}} \cdot {\mathbf{y}}$ is then performed and a new system ${\dot{\mathbf{y}}} = {\mathbf{F}}\left( {\mathbf{y}} \right)$ is composed, where ${\mathbf{F}}_{{\left( {n \times 1} \right)}} = {\mathbf{P}}^{ - 1} \cdot {\mathbf{f}}$. A new Jacobian matrix ${\mathbf{J}}_{\text{Y}}$ is composed in Eq. (24). Matrix ${\mathbf{J}}_{\text{Y}} \left( 0 \right)$ will have the so-called real canonical form, see Eq. (24); set $\omega_{0} = {\mathbf{J}}_{\text{Y}} \left( 0 \right)[2,1]$ and ${\mathbf{D}}$ as shown in Eq. (24).

$${\mathbf{J}}_{\text{Y}} \left( 0 \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{1} }}{{\partial y_{1} }}} & {\frac{{\partial F_{1} }}{{\partial y_{2} }}} & \ldots & {\frac{{\partial F_{1} }}{{\partial y_{n} }}} \\ {\frac{{\partial F_{2} }}{{\partial y_{1} }}} & {\frac{{\partial F_{2} }}{{\partial y_{2} }}} & \ldots & {\frac{{\partial F_{2} }}{{\partial y_{n} }}} \\ \vdots & \vdots & \ldots & \vdots \\ {\frac{{\partial F_{n} }}{{\partial y_{1} }}} & {\frac{{\partial F_{n} }}{{\partial y_{2} }}} & \ldots & {\frac{{\partial F_{n} }}{{\partial y_{n} }}} \\ \end{array} } \right]_{{{\mathbf{y}} = {\mathbf{0}}}} = \left[ {\begin{array}{*{20}c} 0 & { - \omega_{0} } & \vdots \\ {\omega_{0} } & 0 & \vdots \\ \vdots & \vdots & {{\mathbf{D}}_{{\left( {n - 2} \right) \times \left( {n - 2} \right)}} } \\ \end{array} } \right]_{n \times n}$$

(24)

In continue, a sequence of partial derivatives has to be calculated, see Eqs. (25)–(30). The reader should bear in mind that applying the methodology in M-DOF rotors with numerical bearing models, the following partial derivatives can be evaluated only numerically (e.g., Finite Difference Methods) and if not a correct interval is selected in the difference equations, the partial derivative formulas may render wrong values. The reader is advised to proceed from a system of few DOFs in a M-DOF system and keep an eye on the range of values for the following derivatives. In the current work, an interval of 1e-6 was used in the finite difference formulas of the derivatives following.

$$g_{11} = \frac{1}{4}\left[ {\frac{{\partial^{2} F_{1} }}{{\partial y_{1}^{2} }} + \frac{{\partial^{2} F_{1} }}{{\partial y_{2}^{2} }} + {\text{i}}\left( {\frac{{\partial^{2} F_{2} }}{{\partial y_{1}^{2} }} + \frac{{\partial^{2} F_{2} }}{{\partial y_{2}^{2} }}} \right)} \right]$$

(25)

$$g_{02} = \frac{1}{4}\left[ {\frac{{\partial^{2} F_{1} }}{{\partial y_{1}^{2} }} - \frac{{\partial^{2} F_{1} }}{{\partial y_{2}^{2} }} - 2\frac{{\partial^{2} F_{2} }}{{\partial y_{1} \partial y_{2} }} + {\text{i}}\left( {\frac{{\partial^{2} F_{2} }}{{\partial y_{1}^{2} }} - \frac{{\partial^{2} F_{2} }}{{\partial y_{2}^{2} }} + 2\frac{{\partial^{2} F_{1} }}{{\partial y_{1} \partial y_{2} }}} \right)} \right]$$

(26)

$$g_{20} = \frac{1}{4}\left[ {\frac{{\partial^{2} F_{1} }}{{\partial y_{1}^{2} }} - \frac{{\partial^{2} F_{1} }}{{\partial y_{2}^{2} }} + 2\frac{{\partial^{2} F_{2} }}{{\partial y_{1} \partial y_{2} }} + {\text{i}}\left( {\frac{{\partial^{2} F_{2} }}{{\partial y_{1}^{2} }} - \frac{{\partial^{2} F_{2} }}{{\partial y_{2}^{2} }} - 2\frac{{\partial^{2} F_{1} }}{{\partial y_{1} \partial y_{2} }}} \right)} \right]$$

(27)

$$G_{21} = \frac{1}{8}\left[ {\frac{{\partial^{3} F_{1} }}{{\partial y_{1}^{3} }} + \frac{{\partial^{3} F_{1} }}{{\partial y_{1} \partial y_{2}^{2} }} + \frac{{\partial^{3} F_{2} }}{{\partial y_{1}^{2} \partial y_{2} }} + \frac{{\partial^{3} F_{2} }}{{\partial y_{2}^{3} }} + {\text{i}}\left( {\frac{{\partial^{3} F_{2} }}{{\partial y_{1}^{3} }} + \frac{{\partial^{3} F_{2} }}{{\partial y_{1} \partial y_{2}^{2} }} - \frac{{\partial^{3} F_{1} }}{{\partial y_{1}^{2} \partial y_{2} }} - \frac{{\partial^{3} F_{1} }}{{\partial y_{2}^{3} }}} \right)} \right]$$

(28)

At the case that the system is a 2-DOF system (this would be the case of simple model of a journal in a bearing), let $g_{21} = G_{21}$ and evaluate directly the value $c_{1} \left( 0 \right)$ in Eq. (36). Rotor-bearing systems are M-DOF systems, therefore, the following formulas have to be evaluated so as to render $g_{21}$. After defining the elements of vectors ${\mathbf{h}}_{11}$ and ${\mathbf{h}}_{20}$ in Eqs. (29) and (30), the vectors ${\mathbf{w}}_{11}$ and ${\mathbf{w}}_{20}$ are evaluated in Eqs. (31) and (32). All four vectors mentioned here are of size $n - 2$.

$$\mathop h\limits^{k - 2}{}_{11} = \frac{1}{4}\left( {\frac{{\partial^{2} F_{k} }}{{\partial y_{1}^{2} }} + \frac{{\partial^{2} F_{k} }}{{\partial y_{2}^{2} }}} \right),\quad k = 3, \ldots ,n$$

(29)

$$\mathop h\limits^{k - 2}{}_{20} = \frac{1}{4}\left( {\frac{{\partial^{2} F_{k} }}{{\partial y_{1}^{2} }} - \frac{{\partial^{2} F_{k} }}{{\partial y_{2}^{2} }} - 2i\frac{{\partial^{2} F_{k} }}{{\partial y_{1} \partial y_{2} }}} \right),\quad k = 3, \ldots ,n$$

(30)

$${\mathbf{w}}_{11} = - {\mathbf{D}}^{ - 1} \cdot {\mathbf{h}}_{11}$$

(31)

$${\mathbf{w}}_{20} = - \left( {{\mathbf{D}} - 2{\text{i}}\omega_{0} {\mathbf{I}}} \right)^{ - 1} \cdot {\mathbf{h}}_{20}$$

(32)

Then $g_{21}$ is evaluated in Eq. (33), where $\mathop G\limits^{k - 2}{}_{110}$ and $\mathop G\limits^{k - 2}{}_{101}$ are defined in Eqs. (34) and (35) which are written for $k = 3,4, \ldots ,n$.

$$g_{21} = G_{21} + \sum\limits_{k = 1}^{n - 2} {\left( {2\mathop G\limits^{k}{}_{110} \cdot \mathop w\limits^{k}{}_{11} + \mathop G\limits^{k}{}_{101} \cdot \mathop w\limits^{k}{}_{20} } \right)}$$

(33)

$$\mathop G\limits^{k - 2}{}_{110} = \frac{1}{2}\left[ {\frac{{\partial^{2} F_{1} }}{{\partial y_{1} \partial y_{k} }} + \frac{{\partial^{2} F_{2} }}{{\partial y_{2} \partial y_{k} }} + {\text{i}}\left( {\frac{{\partial^{2} F_{2} }}{{\partial y_{1} \partial y_{k} }} - \frac{{\partial^{2} F_{1} }}{{\partial y_{2} \partial y_{k} }}} \right)} \right]$$

(34)

$$\mathop G\limits^{k - 2}{}_{101} = \frac{1}{2}\left[ {\frac{{\partial^{2} F_{1} }}{{\partial y_{1} \partial y_{k} }} - \frac{{\partial^{2} F_{2} }}{{\partial y_{2} \partial y_{k} }} + {\text{i}}\left( {\frac{{\partial^{2} F_{2} }}{{\partial y_{1} \partial y_{k} }} + \frac{{\partial^{2} F_{1} }}{{\partial y_{2} \partial y_{k} }}} \right)} \right]$$

(35)

The quantities evaluated in Eqs. (36)–(39) are included in the period $T$ and the characteristic exponent ${\upbeta }$ of the limit cycle motion is defined in Eq. (39).

The sign of the characteristic exponent $T$ is the indicator for the stability of the limit cycle (periodic motion) and consequently for the type of the bifurcation. When ${\upbeta } < 0$ the limit cycle is stable and the bifurcation is supercritical, see Fig. 2a. When ${\upbeta } > 0$ the limit cycle is unstable and the bifurcation is subcritical, see Fig. 2b.

The response of the system at a stable limit cycle is given from Eq. (40) for $\Omega$ close to $\Omega_{th}$. The proximity of $\Omega$ to $\Omega_{th}$ so as Eq. (B.19) to render confident results of response is a matter beyond the scope of this paper. The reader may check the results of Eq. (B.19) comparing to numerical results. It is advised that $\Omega - \Omega_{th}$ should not exceed few hundredths RPM (200–500 RPM) in a medium speed rotor system of, e.g., $\Omega_{th} = 3800\,{\text{RPM}}$ with its 1st critical speed at, e.g., 1200 RPM (e.g., a slender generator rotor). The envelope $\varepsilon$ of the limit cycles for the various $\Omega$ is given in Eq. (38) and is included also in Eq. (40) through the vector ${\mathbf{y}}$, see Eq. (41), which contains parameter $z$, see Eq. (42).

$$c_{1} = \frac{i}{{2\omega_{0} }}\left( {g_{20} \cdot g_{11} - 2\left| {g_{11} } \right|^{2} - \frac{1}{3}\left| {g_{02} } \right|^{2} } \right) + \frac{{g_{21} }}{2}$$

(36)

$${\text{a}}^{\prime} = {\text{real}}\left( {\lambda^{\prime}_{1} } \right), \quad \omega^{\prime} = {\text{imag}}\left( {\lambda^{\prime}_{1} } \right)$$

(37)

$$\mu_{2} = - \frac{{{\text{real}}\left( {c_{1} } \right)}}{{{\text{a}}^{\prime}}}, \tau_{2} = - \frac{{{\text{imag}}\left( {c_{1} } \right) + \mu_{2} \cdot \omega^{\prime}}}{{\omega_{0} }}, \beta_{2} = 2 \cdot {\text{real}}\left( {c_{1} } \right), \varepsilon = \sqrt {\frac{{\Omega - \Omega_{th} }}{{\mu_{2} }}}$$

(38)

$$T = 2\pi \cdot real\left( {\frac{{1 + \tau_{2} \varepsilon^{2} }}{{\omega_{0} }}} \right), {\upbeta } = \beta_{2} \varepsilon^{2}$$

(39)

$${\mathbf{q}}\left( {\Omega ,t} \right) = {\mathbf{q}}_{*} \left( {\Omega_{th} } \right) + {\mathbf{P}} \cdot {\mathbf{y}}$$

(40)

$$y_{1} = real\left( z \right),\,y_{2} = imag\left( z \right),\,y_{i} = w11_{i - 2} \left| z \right|^{2} + real\left( {w20_{i - 2} z^{2} } \right),\,\quad i = 3,4, \ldots n$$

(41)

$$z = \varepsilon \cdot {\text{e}}^{{\frac{{2\pi \cdot {\text{i}} \cdot t}}{T}}} + \frac{{{\text{i}} \cdot \varepsilon^{2} }}{{6\omega_{0} }}\left( {g_{02} \cdot {\text{e}}^{{\frac{{ - 4\pi \cdot {\text{i}} \cdot t}}{T}}} - 3g_{20} \cdot {\text{e}}^{{\frac{{4\pi \cdot {\text{i}} \cdot t}}{T}}} + 6g_{11} } \right)$$

(42)

Perturbations at the outer of the unstable limit cycle will render a journal motion continuously increasing in extent, and bounded only from physical constraints, e.g., rotor-stator contact. The system will preserve motion close to the bearing shell (high eccentricity) for a while depending on the tolerance of the system in such a hazardous operation.