Keywords

1 Introduction

Droplet impact in liquid pool is a common phenomenon in our day to day life like rain drops, drops from shower but it has also good applicability in spray coating, agriculture (the impact of a raindrop onto the surface of a puddle enhances soil erosion and produces secondary droplets that can act as carriers of spores and bacteria) [1] and many more things. Thus it is a problem of engineering significance.

When a droplet falls in a liquid pool interface dynamics depends on several parameters like velocity of impact on the liquid pool, geometry, the medium through which it travels before it impacts the liquid pool, angle of impact and also on the viscosity and density of the liquid and drop as well [1,2,3,4,5,6,7]. Many literatures have studied these parameters but only few of them address the effect of droplet behaviour by changing the impact velocity.

Hasan et al. [2] at impact velocity of 2.4 m/s, show the phenomena of underwater sound during rain as an outcome of air bubble entrainment in the liquid. Morton et al. [3] in their study have shown the mechanism of formation of bubble due to crater collapse from droplet impact at various velocities of impact. Murat and Donald [4] performed computational analysis of the droplet impact velocity and at solar and lunar surface values of gravity using VOF method in FLUENT. Ray et al. [5] utilized level set formulation to carry forward the work by Morton et al. [3] in order to establish the conditions under which bubble entrapment and jet formation occurs. Orozco and Eduardo in their experimental study followed by computation at an impact velocity of 1.8 m/s suggested that for a jet and its breakup require a balance between surface tension, capillary and viscous forces [1]. Inertia of the pool liquid and drop viscosity are key factors to determine the maximum crater depth is quoted by Jain et al. [6].

Among several available literatures Morton et al. [3] and Ray et al. [5] considered liquid as pure water and studied the impact of water droplet in liquid pool by varying the impact velocity. Morton et al. [3] used high frame rate camera to investigate the falling droplet. The study was conducted at droplet diameter of 3 mm and impact velocity ranging from 0.8 to 2.64 m/s. Ray et al. [5] revised the work on the same droplet diameter using combined level set and volume of fluid method (CLSVOF) in the impact velocity range of 1–4 m/s. Their work reveals a state of transition from coalescence to bouncing with increasing velocity of impact. But still there is void in the study of low impact velocity range as the lowest velocity of impact that has been studied is 0.8 m/s [3].

One such attempt has been made in the current study using commercially available software ANSYS FLUENT. Volume of fluid method (VOF) has been used to study the impact phenomena in the low impact velocity range from 0.2 to 0.6 m/s for a droplet of 3 mm diameter.

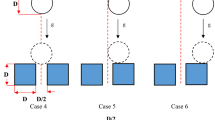
Figure 1 schematically shows a situation when a water droplet begins to impact on a deep water pool. The figure shows H as the initial height of the pool, D as droplet diameter and \({U}_{i}\) as the initial impact velocity. For the present study, air is considered as the surrounding fluid and water as the fluid for the droplet as well as pool.

Fig. 1
figure 1

Schematic representation of a water droplet as it begins to impact on a deep water pool

Full size image

2 Governing Equation and Numerical Methodology

The flow is considered to be two-dimensional (2D) and incompressible. The volume of fluids (VOF) method in FLUENT platform has been used to simulate the present flow problem. In VOF formulation, coupled Navier–Stokes equations (continuity and momentum equations) and VOF equations are solved simultaneously. Properties of each control volume is determined by the presence of component phases in the cell. VOF method solves single momentum equation in the whole domain and depends on the volume fraction of all phases. The dimensional form of the governing equations are as follows.

Defining the volume fraction

$$\alpha = \left\{ \begin{array}{*{20}l} 0& {\text{Gas}} \hfill \\ 0 < \alpha < 1& {\text{Gas-Liquid Interface}} \hfill \\ 1& {\text{Liquid}} \hfill \\ \end{array} \right.$$
(1)

where α is the volume fraction of liquid.

Density (ρ) and viscosity (μ) are calculated as:

Density:

$$\rho = \alpha \rho_{l} + \left( {1 - \alpha } \right)\rho_{g}$$
(2)

Viscosity:

$$\mu = \alpha \mu_{l} + \left( {1 - \alpha } \right)\mu_{g}$$
(3)

Continuity equation:

$$\nabla \cdot \left( {\vec{u}} \right) = 0$$
(4)

Momentum equation:

$$\frac{{\partial \left( {\rho \vec{u}} \right)}}{\partial t} + \nabla \cdot \left( {\rho \vec{u}\vec{u}} \right) = - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \vec{u} + \nabla^{T} \vec{u}} \right)} \right] + \sigma \kappa_{f} n_{f} \delta \left( {x - x_{f} } \right) + \rho \vec{g}$$
(5)

Interface is traced with the following VOF equation:

$$\frac{\partial \alpha }{{\partial t}} + \nabla \cdot \left( {\alpha \vec{u}} \right) = \alpha \left( {\nabla \cdot \vec{u}} \right)$$
(6)

where l is the subscript to denote liquid phase and g is to denote gas phase respectively,\({\kappa }_{f}\) is interface curvature, x is position vector, \({x}_{f}\) is interface position, \({n}_{f}\) and is interface normal and δ is the delta function. Values of density and viscosity are taken from Eqs. (2) and (3) and put in transport equation.

Piecewise linear interface calculation scheme (PLIC) which is available in FLUENT [8] as Geometric Reconstruction Scheme has been used to model the interface. Volume fraction of a phase is calculated with the help of explicit scheme applied to interface tracking equation i.e. Eq. (6) and integrated over control volume. For Pressure–Velocity coupling PISO (Pressure implicit with splitting of operator) algorithm has been used. As the length scale and time scales are small they have been non dimensionalized with respect to the droplet diameter D and the ratio of droplet diameter D to that with impact velocity Ui as \({t}_{\mathrm{ref}}\) = D/Ui. Second order upwinding is used to discretize advection terms.

3 Boundary Conditions

The computational domain is shown schematically in Fig. 2. It is an axisymmetric domain. On the right side is a free slip boundary condition and an axisymmetric boundary condition is set on the left hand side of the computational domain. Lower boundary is a solid wall and no slip condition is considered. Drop of diameter 3 mm has been made using the patch option in fluent solver by assigning its center coordinates and radius. The drop has been patched with an initial velocity of impact Ui. Outflow Boundary condition has been assigned to the top of domain. Pictorial representation of the above mentioned boundary conditions are visible in Fig. 2

Fig. 2
figure 2

Boundary conditions

Full size image

4 Results and Discussion

4.1 Validation

To ensure the accuracy of the present computational work validation of the numerical method has been done. Non dimensionalized crater depth (H/D) has been plotted against the non dimensionalized time and the results have been compared with the work by Morton et al. [3].The drop diameter D has been chosen to be 3 mm and the impact velocity Ui has been chosen to be 1.55 m/s in consistence with parameters of Morton et al. [3] (Fig. 3). Also qualitative validation has been shown at different time steps in Fig. 4. The non dimensionalized time steps at which the results of interface dynamics are compared qualitatively are 6.2 and 8.6.

Fig. 3
figure 3

Validation of variation of crater depth with time (non-dimensional) from the work of Morton et al. [3]

Full size image
Fig. 4
figure 4

Air-water interface comparison with the work by Morton et al. [3] at two time instants

Full size image

Initial deviation is due to the drop being completely spherical (in computational work) as it strikes the pool surface because the drop falling from a certain height in the work by Morton et al. [3] is not completely spherical as it deforms as it travels through a certain height before striking the pool.

4.2 Results of Droplet Impact at Different Impact Velocities

The dynamics of air–water interface at various time instants for a given impact velocities are shown in Fig. 5. As seen, a clear pinch off of secondary droplet is visible at a time instant τ = 0.8 for the impact velocity of 0.2 m/s. In the range of τ = 1.006 to 1.173 for impact velocity of 0.4 m/s secondary droplet can be observed to reach the limiting case of pinch off but still attached to the water in the pool, i.e. disintegration of secondary droplet is not observed while in case of impact velocity of 0.6 m/s full coalescence is observed and for sure there is no pinch off at any time instant. This is in agreement with the work of Morton et al. [3] which reports no pinch off up to impact velocity of 0.8 m/s. A deep crater as compared to other cases (impact velocity of 0.2 and 0.4 m/s) is observed and a column of water is seen rising after drop coalesces for the time range of τ = 0.32 to 8.64 for impact velocity of 0.6 m/s. Figure 6a shows the variation of the crater depth with the impact velocities from which it is evident that there is a sharp decrease of height of free surface as soon as the pinch off takes place (for Ui = 0.2 and 0.4 m/s) and again the free surface height begins to rise when pinched off droplet coalesces. It also indicates the formation of shallow crater for the pinch off case. However, in case of a complete coalescence there is gradual drop in free surface height and also the crater thus formed is deep. From Fig. 5 it is also observed that crater is wider in case of a complete coalescence. Figure 6b shows the variation of pinch off time with the different values of impact velocities. As indicated, time for the secondary droplet to pinch off (or about to pinch off for complete coalescence case) increases with increase in impact velocity.

Fig. 5
figure 5

Instantaneous air–water interface variation with time for different impact velocity

Full size image
Fig. 6
figure 6

a Variation of interface height of free surface with time. b Time of pinch off at different impact velocities

Full size image

Other important observation is a jet circumscribing the droplet (initiated at τ = 0.32 at Ui = 0.6 m/s) moving away as the time progresses can be seen for impact velocity of 0.6 m/s but no such phenomena is occurring for smaller impact velocities i.e. at impact velocity of 0.4 and 0.2 m/s. In the initial stages of impact droplet is seen to be spreading which leads to formation of circumscribing plateau around the region of impact of droplet in case of impact at 0.4 and 0.2 m/s.

In extension to the work by Ray et al. [5], which addresses bubble entrapment and formation of jet to a minimum impact velocity of 1 m/s whereas in the present work droplet bouncing before coalescence is observed. This is unique as a much lower impact velocity range i.e. 0.2 m/s to 0.6 m/s has been studied numerically (using a commercial software FLUENT) considering both droplet and liquid pool to be water.

5 Conclusion

The present numerical study on droplet impact in deep liquid pool at low impact velocities has been carried out in 2D domain in commercially available software ANSYS FLUENT. Satisfactory validation of work by Morton et al. [3] has been carried out initially for authenticity of the present work. To save computational effort only half domain has been used as the problem is symmetric about the axis. Present study reveals that as the impact velocity is lowered there is transition from complete coalescence of droplet to formation of secondary droplet followed by its pinch off. Also the pinch off time and crater depth are found to increase with increase in velocity of impact. A clear pinch off of secondary droplet is observed at τ = 0.2, for the case of impact velocity 0.2 m/s. Complete disintegration of secondary droplet is not visible at impact velocity of 0.4 m/s but it can be concluded to be a threshold velocity below which clear pinch off can be obtained.

Plateau formation around the droplet impact region is reported for impact velocity of 0.2 and 0.4 m/s velocity of impact whereas a circumscribing jet region has formed for impact velocity of 0.6 m/s.