Keywords

1 Introduction

The goal of clustering is to divide a given dataset into different groups such that similar instances are allocated into one group  [22, 33, 34]. Clustering is one of the most classical techniques that has been found to perform surprisingly well  [15, 19, 21]. Clustering has been successfully utilized in various application areas, text mining  [16, 36], voice recognition  [1], image segmentation  [38], to name a few. Up to now, myriads of clustering methods have been designed under the framework of different methodologies and statistical theories  [30, 31], like k-means clustering  [26], spectral clustering  [29], information theoretic clustering  [9], energy clustering  [37], discriminative embedded clustering  [11], multi-view clustering  [12, 20, 23, 32], etc. Among them, k-means, as one of the most popular clustering algorithms, has received considerable attention due to its efficiency and effectiveness since it was introduced in 1967  [26]. Furthermore, it has been categorized as one of the top ten data mining algorithms in term of usage and clustering performance  [39]. There is no doubt that k-means is the most popularly used clustering method in various practical problems  [13].

Recently, the Nonnegative Matrix Factorization (NMF) draws much attention in data clustering and achieves promising performance  [2, 14, 18]. Previous work indicated that NMF is identical to k-means clustering with a relaxed condition  [8]. Until now several variants of k-means have been presented to improve the clustering accuracy. Inspired by the principal component analysis (PCA),  [6] shown that principal components actually provide continuous solutions, which can be treated as the discrete class indicators for k-means clustering. Moreover, the subspace separated by the cluster centroids can be obtained by spectral expansion.  [5] designed a spherical k-means for text clustering with good performance in terms of both solution quality and computational efficiency by employing cosine dissimilarities to perform prototype-based partitioning of weight representations.  [10] extended a kernel k-means clustering to handle multi-view datasets with the help of multiple kernel learning. To explore the sample-specific attributes of data, the authors focused on combining kernels in a localized way.  [27] proposed a fast accelerated exact k-means, which can be considered as a general improvement of existing k-means algorithms with better estimates of the distance bounds.  [28] assumed that incorporates distance bounds into the mini-batch algorithm, data should be preferentially reused. That is, data in a mini-batch at current iteration is reused at next iteration automatically by utilizing the nested mini-batches.

Although the aforementioned k-means methods have shown their effectiveness in many applications, they are typically designed in a single layer formulation. As a result, the mapping between the low-dimensional representation obtained by these methods and the original data may still contain complex hierarchical information. Motivated by the development of deep learning that employs multiple processing layers to explore the hierarchical information hidden in data  [3], in this paper, we propose a novel deep k-means model to learn the hidden information with respect to multiple level characteristics. By utilizing the deep structure to conduct k-means hierarchically, the data hierarchical semantics is learned in a layerwise way. Through the deep k-means structure, instances from same class are pushed closer layer by layer, which is beneficial for the subsequent learning task. Furthermore, we introduce an alternative updating algorithm to address the corresponding optimization problem. Experiments are conducted on benchmark data sets and show promising results of our model compared to several state-of-the-art algorithms.

2 Preliminaries

As mentioned before, NMF is essentially identical to relaxed k-means algorithm  [8]. Before introducing our deep k-means, first we briefly review NMF  [25]. Denote a nonnegative data matrix as \(\mathbf {X}=[x_{1}, x_{2}, \cdots , x_{n}] \in \mathbb {R}^{m\times n}\), where n is the number of instances and m is the feature dimension. NMF tries to search two nonnegative matrices \(\mathbf {U} \in \mathbb {R}^{m\times c}\) and \(\mathbf {V} \in \mathbb {R}^{n\times c}\) such that

$$\begin{aligned} \begin{aligned}&J_{NMF} =\sum _{i=1}^{n}\sum _{j=1}^{m}\Big (\mathbf {X}_{ij}-(\mathbf {UV}^{T})_{ij}\Big )^{2} =\Vert \mathbf {X}-\mathbf {UV}^{T}\Vert _{F}^{2} \\&\qquad \qquad \qquad \qquad \mathrm{{s.t.}}\, \mathbf {U} \ge 0, \mathbf {V} \ge 0, \end{aligned} \end{aligned}$$
(1)

where \(\Vert \cdot \Vert _{F}\) indicates a Frobenius norm and \(\mathbf {X}_{ij}\) is the (i, j)-th element of \(\mathbf {X}\).  [25] proved that Eq. (1) is not jointly convex in \(\mathbf {U}\) and \(\mathbf {V}\) (i.e., convex in \(\mathbf {U}\) or \(\mathbf {V}\) only), and proposed the following alternative updating rules to search the local minimum:

$$\begin{aligned} \mathbf {U}_{ij}\quad \leftarrow \quad \mathbf {U}_{ij}\frac{(\mathbf {X}\mathbf {V})_{ij}}{(\mathbf {U}\mathbf {V}^{T}\mathbf {V})_{ij}}, \\ \mathbf {V}_{ij}\quad \leftarrow \quad \mathbf {V}_{ij}\frac{(\mathbf {X}^{T}\mathbf {U})_{ij}}{(\mathbf {V}\mathbf {U}^{T}\mathbf {U})_{ij}}, \end{aligned}$$

where \(\mathbf {V}\) denotes the class indicator matrix in unsupervised setting  [17], \(\mathbf {U}\) denotes the centroid matrix, and c is cluster number. Since \(c\ll n\) and \(c\ll m\), NMF actually tries to obtain a low-dimensional representation \(\mathbf {V}\) of the original input \(\mathbf {X}\).

Real-world data sets are rather complex that contain multiple hierarchical modalities (i.e., factors). For instance, face data set typically consists several common modalities like pose, scene, expression, etc. Traditional NMF with single layer formulation is obviously unable to fully uncover the hidden structures of the corresponding factors. Therefore,  [35] proposed a multi-layer deep model based on semi-NMF to exploit hierarchical information with respect to different modalities. And models a multi-layer decomposition of an input data \(\mathbf {X}\) as

$$\begin{aligned} \begin{aligned} \mathbf {X}&\approx \mathbf {U}_1\mathbf {V}_1^{T}, \\ \mathbf {X}&\approx \mathbf {U}_1\mathbf {U}_2\mathbf {V}_2^{T}, \\&\vdots \\ \mathbf {X}&\approx \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}, \end{aligned} \end{aligned}$$
(2)

where r means the number of layers, \(\mathbf {U}_i\) and \(\mathbf {V}_i\) respectively denote the i-th layer basis matrix and representation matrix. It can be seen that deep semi-NMF model also focuses on searching a low-dimensional embedding representation that targets to a similar interpretation at the last layer, i.e., \(\mathbf {V}_r\). The deep model in Eq. (2) is able to automatically search the latent hierarchy by further factorizing \(\mathbf {V}_i (i<r)\). Furthermore, this model is able to discover representations suitable for clustering with respect to different modalities (e.g., for face data set, \(\mathbf {U}_3\) corresponds to the attributes of expressions, \(\mathbf {U}_2\mathbf {U}_3\) corresponds to the attributes of poses, and \(\mathbf {U}=\mathbf {U}_1\mathbf {U}_2\mathbf {U}_3\) finally corresponds to identities mapping of face images). Compared to traditional single layer NMF, deep semi-NMF provides a better ability to exploit the hidden hierarchical information, as different modalities can be fully identified by the obtained representations of each layer.

3 The Proposed Method

In this section, we introduce a novel deep k-means model for data clustering, followed with its optimization algorithm.

3.1 Deep K-Means

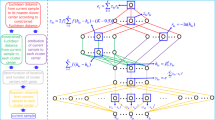
Traditional k-means methods are typically designed in a single layer formulation. Thus the mapping between the obtained low-dimensional representation and the original data may contain complex hierarchical information corresponding to the implicit modalities. To exploit such hidden representations with respect to different modalities, we propose a novel deep k-means model by utilizing the deep structure to conduct k-means hierarchically. The hierarchical semantics of the original data in our model is comprehensively learned in a layerwise way. To improve the robustness of our model, the sparsity-inducing norm, \(l_{2,1}\)-norm, is used in the objective. Since \(l_{2,1}\)-norm based residue calculation adopts the \(l_{2}\)-norm within a data point and the \(l_{1}\)-norm among data points, the influence of outliers is reduced by the \(l_{1}\)-norm  [24]. Moreover, the non-negative constraint on \(\mathbf {U}_i\) is removed such that the input data can consist of mixed signs, thus the applicable range of the proposed model is obviously enlarged. Since the non-negativity constraints on \(V_i\) make them more difficult to be optimized, we introduce new variables \(V_i^+\) to which the non-negativity constraints are applied, with the constraints \(V_i=V_i^+\). In this paper, we utilize the alternating direction method of multipliers (ADMM)  [4] to handle the constraint with an elegant way, while maintain the separability of the objective. As a result, the non-negativity constraints are effectively incorporated to our deep k-means model. Our deep k-means model (DKM) is stated as

$$\begin{aligned} \begin{aligned}&\qquad \qquad \qquad \quad \,\,\, J_{DKM} = \Vert \mathbf {X}-\mathbf {Y}\Vert _{2,1} \\&\mathrm{s.t.} \mathbf {Y} = \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}, \left( \mathbf {V}_r\right) _{.c} =\{0,1\}, \sum _{c=1}^{C}\left( \mathbf {V}_r\right) _{.c}=1,\\&\qquad \qquad \,\,\, \mathbf {V}_i = \mathbf {V}_i^+, \mathbf {V}_i^+ \ge 0, i\in [1, \ldots , r-1]. \end{aligned} \end{aligned}$$
(3)

While \(\Vert \mathbf {X}-\mathbf {Y}\Vert _{2,1}\) is simple to minimize with respect to \(\mathbf {Y}\), \(\Vert \mathbf {X}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\Vert _{2,1}\) is not simple to minimize with respect to \(\mathbf {U}_i\) or \(\mathbf {V}_i\). Multiplicative updates implicitly address the problem such that \(\mathbf {U}_i\) and \(\mathbf {V}_i\) decouple. In ADMM context, a natural formulation would be to minimize \(\Vert \mathbf {X}-\mathbf {Y}\Vert _{2,1}\) with the constraint \(\mathbf {Y} = \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\). This is the core reason why we choose to solve such a problem like Eq. (3). In addition, each row of \(\mathbf {V}_r\) in Eq. (3) is enforced to satisfy the 1-of-C coding scheme. Its primary goal is to ensure the uniqueness of the final solution \(\mathbf {V}_r\).

The augmented Lagrangian of Eq. (3) is

$$\begin{aligned} \begin{aligned}&\mathcal {L}(\mathbf {Y},\mathbf {U}_i,\mathbf {V}_i,\mathbf {V}_i^+,\varvec{\mu },\varvec{\lambda }_i) = \Vert \mathbf {X}-\mathbf {Y}\Vert _{2,1} +{<}\varvec{\mu },\mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}{>} \\ +&\frac{\rho }{2}\Vert \mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\Vert _{F}^{2} +\sum _{i=1}^{r-1}{<}\varvec{\lambda }_i,\mathbf {V}_i - \mathbf {V}_i^+{>} +\frac{\rho }{2}\sum _{i=1}^{r-1}\Vert \mathbf {V}_i - \mathbf {V}_i^+\Vert _{F}^{2}, \end{aligned} \end{aligned}$$
(4)

where \(\varvec{\mu }\) and \(\varvec{\lambda }_i\) are Lagrangian multipliers, \(\rho \) is the penalty parameter, and \({<}\cdot ,\cdot {>}\) represents the inner product operation.

The alternating direction method for Eq. (4) is derived by minimizing \(\mathcal {L}\) with respect to \(\mathbf {Y},\mathbf {U}_i,\mathbf {V}_i,\mathbf {V}_i^+\), one at a time while fixing others, which will be discussed below.

3.2 Optimization

In the following, we propose an alternative updating algorithm to solve the optimization problem of the proposed objective. We update the objective with respect to one variable while fixing the other variables. This procedure repeats until convergence.

Before the minimization, first we perform a pre-training by decomposing the data matrix \(\mathbf {X}\approx \mathbf {U}_1\mathbf {V}_1^{T}\), where \(\mathbf {V}_1\in \mathbb {R}^{n\times k_1}\) and \(\mathbf {U}_1\in \mathbb {R}^{m\times k_1}\). The obtained representation matrix \(\mathbf {V}_1\) is then further decomposed as \(\mathbf {V}_1\approx \mathbf {U}_2\mathbf {V}_2^{T}\), where \(\mathbf {V}_2\in \mathbb {R}^{n\times k_2}\) and \(\mathbf {U}_2\in \mathbb {R}^{k_1\times k_2}\). We respectively denote \(k_1\) and \(k_2\) as the dimensionalities of the first layer and the second layerFootnote 1. Continue to do this, finally all layers are pre-trained, which would greatly improve the training time as well as the effectiveness of our model. This trick has been applied favourably in deep autoencoder networks  [4].

Optimizing Eq. (4) is identical to minimizing the formulation as follows

$$\begin{aligned} \begin{aligned}&\mathcal {L}(\mathbf {Y},\mathbf {U}_i,\mathbf {V}_i,\mathbf {V}_i^+,\varvec{\mu },\varvec{\lambda }_i) = \mathrm{Tr}\left( \left( \mathbf {X}-\mathbf {Y}\right) \mathbf {D}\left( \mathbf {X}-\mathbf {Y}\right) ^{T}\right) \\ +&\frac{\rho }{2}\mathrm{Tr}\left( \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) ^{T}\right) \\&+\,{<}\varvec{\mu },\mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}{>} +\sum _{i=1}^{r}{<}\varvec{\lambda }_i,\mathbf {V}_i - \mathbf {V}_i^+{>} \\&\qquad \quad \,\, +\frac{\rho }{2}\sum _{i=1}^{r}\mathrm{Tr}\left( \left( \mathbf {V}_i - \mathbf {V}_i^+\right) \left( \mathbf {V}_i - \mathbf {V}_i^+\right) ^{T}\right) , \end{aligned} \end{aligned}$$
(5)

where \(\mathbf {D}\) is a diagonal matrix and its j-th diagonal element is

$$\begin{aligned} {d}_{j}=\frac{1}{2\Vert \mathbf {e}_j\Vert _{2}}. \end{aligned}$$
(6)

and \(\mathbf {e}_j\) is the j-th column of the following matrix

$$\begin{aligned} \mathbf {E}=\mathbf {X}-\mathbf {Y}. \end{aligned}$$
(7)

Updating \(\mathbf {U}_{\textit{\textbf{i}}}\) Minimizing Eq. (4) w.r.t. \(\mathbf {U}_i\) is identical to solving

$$\begin{aligned} \begin{aligned}&\qquad \qquad \,\,\, \mathcal {L}_{U}={<}\varvec{\mu },\mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}{>} \\ +\,&\frac{\rho }{2}\mathrm{Tr}\left( \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) ^{T}\right) . \end{aligned} \end{aligned}$$
(8)

Calculating the derivative of \(\mathcal {L}_{U}\) w.r.t. \(\mathbf {U}_i\) and setting it to zero, then we have

$$\begin{aligned} \mathbf {U}_i = \left( \varvec{\varPhi }^{T}\varvec{\varPhi }\right) ^{-1}\left( \varvec{\varPhi }^{T}\mathbf {Y}\widetilde{\mathbf {V}_i}+\frac{\varvec{\varPhi }^{T}\varvec{\mu }\widetilde{\mathbf {V}_i}}{\rho }\right) \left( \widetilde{\mathbf {V}_i}^{T}\widetilde{\mathbf {V}_i}\right) ^{-1}, \end{aligned}$$
(9)

where \(\varvec{\varPhi } = \mathbf {U}_1\mathbf {U}_2\cdots \mathbf {U}_{i-1}\) and \(\widetilde{\mathbf {V}_i}\) denotes the reconstruction of the i-th layer’s centroid matrix.

Updating \(\mathbf {V}_{\textit{\textbf{i}}}\) \(\varvec{(i<r)}\) Minimizing Eq. (4) w.r.t. \(\mathbf {V}\) is identical to solving

$$\begin{aligned} \begin{aligned}&\qquad \qquad \quad \mathcal {L}_{V}=\,<\varvec{\mu },\mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}> \\ +&\frac{\rho }{2}\mathrm{Tr}\left( \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) ^{T}\right) \\ +&\sum _{i=1}^{r}{<}\varvec{\lambda }_i,\mathbf {V}_i - \mathbf {V}_i^+{>} +\frac{\rho }{2}\sum _{i=1}^{r}\mathrm{Tr}\left( \left( \mathbf {V}_i - \mathbf {V}_i^+\right) \left( \mathbf {V}_i - \mathbf {V}_i^+\right) ^{T}\right) . \end{aligned} \end{aligned}$$
(10)

Similarly, calculating the derivative of \(\mathcal {L}_{V}\) w.r.t. \(\mathbf {V}_i\), and setting it to zero, we obtain

$$\begin{aligned} \mathbf {V}_i = \left( \mathbf {Y}^{T}\varvec{\varPhi }\mathbf {U}_{i}+\mathbf {V}_{i}^{+}+\frac{\varvec{\mu }^{T}\varvec{\varPhi }\mathbf {U}_{i}}{\rho }-\frac{\varvec{\lambda }_i}{\rho }\right) \left( \mathbf {I}+\mathbf {U}_{i}^{T}\varvec{\varPhi }^{T}\varvec{\varPhi }\mathbf {U}_{i}\right) ^{-1}, \end{aligned}$$
(11)

where \(\mathbf {I}\) represents an identity matrix.

Updating \(\mathbf {V}_{\textit{\textbf{r}}}\) \(\big ({\mathbf {i.e.,}}\, \mathbf {V}_{\textit{\textbf{i}}}, \varvec{ (i=r)}\big )\) We update \(\mathbf {V}_r\) by solving

$$\begin{aligned} \begin{aligned}&J_{V_r} = \min _{\mathbf {V}_r}\Vert \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\Vert _{2,1} = \min _{\mathrm{v}}\sum _{j=1}^{n}{d}_j\Vert \mathrm{x}_j-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathrm{v}_j\Vert _{2}^{2} \\&\qquad \qquad \qquad \qquad \,\, \mathrm{s.t.}\,\left( \mathbf {V}_r\right) _{.c} =\{0,1\}, \sum _{c=1}^{C}\left( \mathbf {V}_r\right) _{.c}=1, \end{aligned} \end{aligned}$$
(12)

where \(\mathrm{x}_j\) denotes the j-th data sample of \(\mathbf {X}\), and \(\mathrm{v}_j\) denotes the j-th column of \(\mathbf {V}_r^T\). Taking a closer look at Eq. (12), we can see that it is independent between different j. Thus we can independently solve it one by one:

$$\begin{aligned} \begin{aligned}&\min _{\mathrm{v}}\left( {d}\Vert \mathrm{x}-\mathbf {U}_1\mathbf {U}_2\cdots \mathbf {U}_r\mathrm{v}\Vert _{2}^{2}\right) \\&\mathrm{s.t.} v_{c}=\{0,1\}, \sum _{c=1}^{C}v_{c}=1. \end{aligned} \end{aligned}$$
(13)

Since v is coded by 1-of-C scheme, there exists C candidates that could be the solution of Eq. (13). And each individual solution is exactly the c-th column of identity matrix \(\mathbf {I}_C=[\mathbf {f}_1,\mathbf {f}_2,\cdots ,\mathbf {f}_C]\). Thus the optimal solution can be obtained by performing an exhaustive search, i.e.,

$$\begin{aligned} \mathrm{v}^{*}=\mathbf {f}_c, \end{aligned}$$
(14)

where c is given by

$$\begin{aligned} c=\mathop {\mathrm {arg\,min}}\limits _{\overline{c}}\left( {d}\Vert \mathrm{x}-\mathbf {U}_1\mathbf {U}_2\cdots \mathbf {U}_r\mathbf {f}_{\overline{c}}\Vert _{2}^{2}\right) . \end{aligned}$$
(15)

Updating \(\mathbf {Y}\) Minimizing Eq. (4) w.r.t. \(\mathbf {Y}\) is identical to solving

$$\begin{aligned} \begin{aligned}&\qquad \qquad \,\, \mathcal {L}_{Y} = \mathrm{Tr}\left( \left( \mathbf {X}-\mathbf {Y}\right) \mathbf {D}\left( \mathbf {X}-\mathbf {Y}\right) ^{T}\right) \\ +&\,\frac{\rho }{2}\mathrm{Tr}\left( \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) \left( \mathbf {Y}-\mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}\right) ^{T}\right) \\&\qquad \qquad \quad +\,{<}\varvec{\mu },\mathbf {Y} - \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}{>}. \end{aligned} \end{aligned}$$
(16)

Calculating the derivative of \(\mathcal {L}_{Y}\) w.r.t. \(\mathbf {Y}\) and setting it to 0, we have

$$\begin{aligned} \mathbf {Y}=\left( 2\mathbf {XD}+\rho \mathbf {U}_1\mathbf {U}_2 \cdots \mathbf {U}_r\mathbf {V}_r^{T}-\varvec{\mu }\right) \left( 2\mathbf {D}+\rho \mathbf {I}\right) ^{-1}. \end{aligned}$$
(17)

Updating \(\mathbf {V}_{\textit{\textbf{i}}}^+\) Minimizing Eq. (4) w.r.t. \(\mathbf {V}_i^+\) is identical to solving

$$\begin{aligned} \mathcal {L}_{{V}^+}=\sum _{i=1}^{r}{<}\varvec{\lambda }_i,\mathbf {V}_i - \mathbf {V}_i^+{>} +\frac{\rho }{2}\sum _{i=1}^{r}\mathrm{Tr}\left( \left( \mathbf {V}_i - \mathbf {V}_i^+\right) \left( \mathbf {V}_i - \mathbf {V}_i^+\right) ^{T}\right) . \end{aligned}$$
(18)

Calculating the derivative of \(\mathcal {L}_{{V}^+}\) w.r.t. \(\mathbf {V}_i^+\) and setting it to 0, we get

$$\begin{aligned} \mathbf {V}_i^+=\mathbf {V}_i+\frac{\varvec{\lambda }_i}{\rho }. \end{aligned}$$
(19)

In summary, we optimize the proposed model by orderly performing the above steps. This procedure repeats until convergence.

Fig. 1.
figure 1

COIL dataset.

Full size image

4 Experiments

To validate the effectiveness of our method. We compare it with the classical k-means  [26], NMF  [25], Orthogonal NMF (ONMF)  [8], Semi-NMF (SNMF)  [7], \(l_{2,1}\)-NMF  [24] and the deep Semi-NMF (DeepSNMF)  [35].

Table 1. Characteristics of experimental data sets.
Full size table

4.1 Data Sets

We empirically evaluate the proposed method on six benchmark data setsFootnote 2. As a demonstration, Fig. 1 shows the dataset COIL. Table 1 shows the specific characteristics of all datasets. The number of instances is ranged from 400 to 4663, and feature number is ranged from 256 to 7511.

4.2 Parameter Setting

For k-means algorithm, we perform k-means on each data set until it convergence. And the corresponding results are treated as the final result of k-means. We also use this result as the initialization of all other compared methods for fairness. For each compared method, the optimal value is solved based on the parameter setting range recommended by the relevant literature, and then the result under this condition is regarded as the final result output. For the proposed deep method, the layer sizes (as described in Sect. 3.2) are set as [100 c], [50 c] and [100 50 c] for simplicity. As for parameter \(\rho \), we search it from {1e−5, 1e−4, 1e−3, 0.01, 0.1, 1, 10, 100}.

Under each parameter setting, we repeat the experiments 10 times for all methods, and the average results are reported for fair comparison.

4.3 Results and Analysis

The clustering performance measured by clustering accuracy (ACC) and normalized mutual information (NMI) of all methods are given in Tables 2-3. It is obvious that our method has better results than other algorithms. The superiority of DKM verifies that it could better explore cluster structure by uncovering the hierarchical semantics of data. That is, by utilizing the deep framework to conduct k-means hierarchically, the hidden structure of data is learned in a layerwise way, and finally, a better high-level, final-layer representation can be obtained for clustering task. By leveraging the deep framework and k-means model, the proposed DKM can enhance the performance of data clustering in general cases.

Table 2. Clustering results of ACC on all data sets.
Full size table
Table 3. Clustering results of NMI of on all data sets.
Full size table

Based on the theoretical analysis and empirical results presented in this paper, it would be interesting to combine deep structure learning and classical machine learning models into a unified framework. By taking advantages of the both learning paradigms, more promising results in various learning tasks can be expected.

5 Conclusion

In this paper, we propose a novel deep k-means model to learn the hidden information with respect to multiple level characteristics. By utilizing the deep structure to conduct k-means hierarchically, the data hierarchical semantics is learned in a layerwise way. Through the deep k-means structure, instances from same class are pushed closer layer by layer, which benefits the subsequent clustering task. We also introduce an alternative updating algorithm to address the corresponding optimization problem. Experiments are conducted on six benchmark data sets and show promising results of our model against several state-of-the-art algorithms.