Performance Evaluation of Composite Fading Channels Using q-Weibull Distribution

Abstract

In wireless communication systems, the received signal is superimposed by the contemporaneous effects of both shadowing and multipath fading. The conventional composite models fail to capture the outliers in the fading channels. In this context, we portray the significance of the Tsallis’ non-extensive parameter ‘q’ in modeling various fading environments. This paper exploits the well-known q-Weibull probability density function (pdf) in characterizing the composite fading channels. The q-Weibull pdf yields a tight agreement over the generated fading signals. Furthermore, the different performance metrics, viz. amount of fading, average channel capacity, and outage probability, are obtained in closed form. The derived results are validated using rigorous Monte Carlo simulation procedure.

1 Introduction

In real-life propagation scenarios, the wireless communication channels get simultaneously impaired by shadowing and multipath fading. This phenomena in wireless communication systems leads to a composite fading environment [1,2,3]. Several models have been propounded to characterize the multipath fading phenomena, viz. Rician, Rayleigh, Weibull, and Nakagami, whereas shadowing is modeled using distributions such as the Inverse Gamma, Gamma, and Lognormal [1, 3]. These distributions can be superimposed to characterize the contemporaneous effects of both shadowing and fading. For this purpose, different composite models, viz. the Weibull-lognormal (WL), Nakagami-lognormal, and Rayleigh-lognormal [4,5,6,7], have been suggested. However, the lognormal-based mixture models are mathematically intractable which requires several approximations techniques to obtain the desired results. In contrast, the entropy-based approach characterizes the various fading channels in continuous range of Tsallis’ non-extensive parameter ‘q’.

It is worth noting that the Weibull distribution [1, 4, 8, 9] is best suited to model multipath fading channels and its proficiency can be extended by introducing the Tsallis’ non-extensive parameter ‘q’ [10, 11]. The q-Weibull distribution [12] can characterize both multipath and shadowing effects simultaneously by varying the continuous interval of non-extensive parameter ‘q’. In contrast to the conventional composite models, for $q>1$ this model has a long-tailed behavior which provides a better fit to the tail fluctuations in the fading signals [13].

In this paper, the importance of q-Weibull distribution [12] is portrayed to characterize the composite fading scenarios. The different performance metrics, viz. the outage probability $(P_{out})$, average channel capacity, and amount of fading (AOF), are expressed in closed form. It is observed that the results obtained are analytically tractable and the obtained measures are found to be in close agreement with the Monte Carlo simulation results.

The remaining paper proceeds as follows: Section 2 illustrates the q-Weibull distribution. Section 3 portrays the importance of q-Weibull model in contrast to the well-known Weibull-lognormal distribution in capturing composite fading environments. The numerical and simulation results for the performance measures have been discussed in Sect. 4. Finally, Sect. 5 provides the conclusion and future works.

2 The q-Weibull Distribution

The pdf of q-Weibull distribution can be defined as [12]:

$$\begin{aligned} f(\gamma ) = {\gamma ^{\alpha - 1}}\alpha {\lambda ^\alpha }\left( {2 - q} \right) {\left[ {1 - (1 - q){{({\lambda ^2}{\gamma ^2})}^{\frac{\alpha }{2}}}} \right] ^{ \frac{1}{{1 - q}}}}, \gamma >0, 1<q<2, \end{aligned}$$

(1)

where $\alpha >0$ is the fading parameter, $\lambda >0$ represents the scale parameter, and $\gamma$ is the received signal-to-noise ratio (SNR). When $q\rightarrow 1$, Eq. 1 converges to the well-known Weibull distribution. Furthermore, for q>1 the q-Weibull distribution follows a long-tailed behavior which enables it to smoothly characterize the tail fluctuations in the fading signals.

Fig. 1.

Plot of (q-Weibull pdf) against SNR ($\gamma$) for different values of q)

Fig. 2.

Illustration of (Weibull-lognormal) distribution corresponding to synthetic signal

From Fig. 1, it is observed that as q approaches 2, the phenomena of long-tailed distributions are obtained and similarly as $q\rightarrow 1$, the curve becomes peaked and mimics the Weibull distribution.

3 Significance of q-Weibull Model

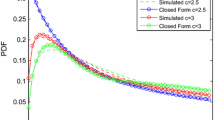
It is well known that shadowing effects are characterized by lognormal distribution [1, 3]. However, the conventionally used lognormal-based composite models, viz. Rayleigh-lognormal, WL models are inefficacious in characterizing the tail fluctuations in the fading signals [13]. In Fig.2, it is observed that the well-known WL model [4, 5] fails to provide a better fit to the synthetic fading signals. The fading signals are generated using MATLAB to mimic the real-time fading scenarios. However, it is possible that the entropy-based q-Weibull distribution can characterize the entire outliers in the fading channels. In this context, the q-Weibull model provides a better fit to the outliers in the fading signals for $1<q<2$. The generated fading signals are well characterized by the q-Weibull distribution corresponding to $q=1.3$ as shown in Fig. 3.

Fig. 3.

Illustration of (q-Weibull distribution) corresponding to synthetic signal for (q = 1.3)

4 Numerical Results and Discussions

In this section, various performance metrics in wireless communications systems, viz. average channel capacity, amount of fading, outage probability in correspondence to the q-Weibull model, have been illustrated. Furthermore, the obtained measures are found to be in closed agreement with the simulation results (Fig. 4).

4.1 Amount of Fading

In wireless fading scenarios, the amount of fading (AOF) is an important performance metric as it specifies the severity of fading and is given as [4, 5]:

$$\begin{aligned} \textit{AOF} = \frac{{E[{\gamma ^2}]}}{{{{\left( {E[\gamma ]} \right) }^2}}} - 1 \end{aligned}$$

(2)

The rth moment of $\gamma$ is obtained as:

$$\begin{aligned} E[{\gamma ^r}] = \int \limits _0^\infty {{\gamma ^r} \times }{\gamma ^{\alpha - 1}} \alpha {\lambda ^\alpha }\left( {2 - q} \right) {\left[ {1 - (1 - q){{({\lambda ^2}{\gamma ^2})}^{\frac{\alpha }{2}}}} \right] ^{ \frac{1}{{1 - q}}}}d\gamma \end{aligned}$$

(3)

or,

$$\begin{aligned} \begin{array}{l} E[{\gamma ^r}] = \frac{{{\lambda ^\alpha }\left( {2 - q} \right) }}{{\Gamma \left( {\frac{1}{{q - 1}}} \right) }}\left[ {{{\left( {\left( {q - 1} \right) {\lambda ^\alpha }} \right) }^{ - \left( {1 + \frac{r}{\alpha }} \right) }}\Gamma \left( {1 + \frac{r}{\alpha }} \right) \Gamma \left( { - 1 - \frac{r}{\alpha } + \frac{1}{{q - 1}}} \right) } \right] \end{array} \end{aligned}$$

(4)

From Eqs. (2) and (4), analytical expression for AOF is given as:

$$\begin{aligned} \begin{array}{l} \textit{AOF} = \left\{ {\frac{{{{\left( {\left( {q - 1} \right) {\lambda ^\alpha }} \right) }^{ - \left( {1 + \frac{2}{\alpha }} \right) }}\Gamma \left[ {1 + \frac{2}{\alpha }} \right] \Gamma \left[ { - 1 - \frac{2}{\alpha } + \frac{1}{{q - 1}}} \right] }}{{{{\left( {\left( {q - 1} \right) {\lambda ^\alpha }} \right) }^{ - 2\left( {1 + \frac{2}{\alpha }} \right) }}{\Gamma ^2}\left[ {1 + \frac{1}{\alpha }} \right] {\Gamma ^2}\left[ { - 1 - \frac{1}{\alpha } + \frac{1}{{q - 1}}} \right] }} \times \frac{{\Gamma \left[ {\frac{1}{{q - 1}}} \right] }}{{{\lambda ^\alpha }\left( {2 - q} \right) }}} \right\} - 1 \end{array} \end{aligned}$$

(5)

Fig. 4.

Analytical solution with simulation results for amount of fading against fading parameter ($\alpha$) corresponding to different q

4.2 Average Channel Capacity

It is an important performance metric that defines the maximum transmission rate a channel achieves with a small probability of error. In ergodic sense, the average channel capacity is expressed as [5, 14]:

$$\begin{aligned} \frac{C}{B} = \frac{1}{{\ln (2)}}\int \limits _0^\infty {\ln (1 + \gamma ){f}(\gamma )d\gamma }, \end{aligned}$$

(6)

where B denotes the bandwidth of the fading channel. Equation(1) and Eq.(6) yield:

$$\begin{aligned} \frac{C}{B} = \frac{1}{{\ln (2)}}\int \limits _0^\infty {\alpha {\lambda ^\alpha }\left( {2 - q} \right) } {\ln (1 + \gamma ){\gamma ^{\alpha - 1}} \times } {\left[ {1 - (1 - q){{({\lambda ^2}{\gamma ^2})}^{\frac{\alpha }{2}}}} \right] ^{ \frac{1}{{1 - q}}}}d\gamma \end{aligned}$$

(7)

As Eq. (7) is not analytically tractable, using Meijer’s G approximations of the polynomials [15]; $\ln (1 + \gamma ) = \mathop G\nolimits _{22}^{12} \left[ {\gamma \left| {_{1,0}^{1,1}} \right. } \right]$ and $\exp ( - \gamma ) = \mathop G\nolimits _{01}^{10} \left[ {\gamma \left| {_0^.} \right. } \right]$, Eq. (7) becomes:

$$\begin{aligned} \frac{C}{B} = \frac{{\alpha {\lambda ^\alpha }}}{{\ln (2)}}\int \limits _0^\infty {\mathop {{\gamma ^{\alpha - 1}}G}\nolimits _{22}^{12} \left[ {\gamma \left| {_{1,0}^{1,1}} \right. } \right] \mathop G\nolimits _{01}^{10} \left[ {{{({\lambda ^2}{\gamma ^2})}^{\frac{\alpha }{2}}}\left| {_0^.} \right. } \right] d\gamma } \end{aligned}$$

(8)

Using Eq. (8) and the substitutions in [16], the average channel capacity is obtained as:

$$\begin{aligned} \frac{C}{B} = \frac{{\alpha {\lambda ^\alpha }}}{{\ln (2)}}H_{23}^{31}\left[ {{\lambda ^\alpha }\left| {_{(0,1),( - \alpha , - \alpha ),( - \alpha ,\alpha )}^{( - \alpha ,\alpha ),(1 - \alpha ,\alpha )}} \right. } \right] \end{aligned}$$

(9)

Fig. 5.

Plot of average channel capacity against fading parameter ($\alpha$) corresponding to different values of parameter q

In Fig. 5, it is evident that the analytical and simulation results of average channel capacity are in close agreement with each other when $q\rightarrow 1$.

4.3 Outage Probability

It is one of the significant performance measures for communications systems over several fading channels. It is denoted as $P_{out}$ and defining the probability of output SNR $\gamma$ under a specified threshold value $\gamma _{th}$ [4, 5] (Fig. 6). It is expressed as [1]

$$\begin{aligned} {P_{out}} = \int \limits _0^{{\gamma _{th}}} {f(\gamma )d\gamma } \end{aligned}$$

(10)

Equations (1) and (10) yield:

$$\begin{aligned} {P_{out}} = \alpha {\lambda ^\alpha }\left( {2 - q} \right) \int \limits _0^{{\gamma _{th}}} {{\gamma ^{\alpha - 1}}{{\left[ {1 - (1 - q){{({\lambda }{\gamma })}^{{\alpha }}}} \right] }^{ \frac{1}{{1 - q}}}}d\gamma } \end{aligned}$$

(11)

Hence, outage probability can be obtained as:

$$\begin{aligned} {P_{out}} = 1 - {\left( {1 + {\gamma _{th}}^\alpha \left( {q - 1} \right) {\lambda ^\alpha }} \right) ^{1 + \frac{1}{{1 - q}}}} \end{aligned}$$

(12)

Fig. 6.

Analytical solution with simulation results for $P_{out}$ against threshold SNR for different $\alpha$

5 Conclusion and Future Work

The theoretical results of the important performance metrics, viz. outage probability, average channel capacity, and amount of fading with respect to the q-Weibull model, were derived. It is profound that Weibull distribution incorporated with the Tsallis’ non-extensive parameter ‘q’ can characterize the composite fading channels. The q-Weibull model captured both fast fading and shadowing effects corresponding to different wireless communication channels for continuous interval of the non-extensive parameter ‘q’, i.e., $1<q<2$. It is worth noting that the q-Weibull model provided a better fit with the synthetic fading signal corresponding to q=1.3 and also characterized the tail fluctuations in the fading signal in contrast to the composite WL model. It would be interesting and challenging in characterizing fading channels and computation of the symbol error probability using the aforementioned ‘q’-Weibull model over the other existing complex models on the basis of non-extensive parameter ‘q’.