Flexural Response of a Plate on Viscoelastic Foundation

Abstract

A mechanical model has been proposed to study the flexural response of a square plate resting on the viscoelastic foundation. A Burgers model is the series combination of Maxwell and Kelvin model, representing viscoelastic behaviour of soil very efficiently, and therefore, the same has been employed to idealize the foundation soil. The foundation has been modelled as a plate, and its time-dependent behaviour has been studied. Classical Kirchhoff’s theory of thin plates has been employed to undertake the flexural analysis of the plate. Governing differential equations have been derived and solved using the finite difference method with the help of appropriate boundary conditions. The results of a particular case of present work have been compared with those available in the literature in order to validate the proposed model. After validation, first the retardation time of the viscoelastic model, representing degree of rigidity of viscoelastic material, has been determined. Detailed parametric study has then been carried out to study the influence of various input parameters like magnitude of applied load, relative magnitude of elastic and viscous coefficients of Burgers model, tension in elastic membrane and the degree of consolidation, on response of plate in terms of its deflection and the bending moment. This work finds direct application in the analysis of raft foundations and rigid pavements.

1 Introduction

Plates resting on viscoelastic foundation bed can represent the time-dependent behaviour of foundation. Over the years, plate elements are used for the idealization of raft foundations, lock-type structures, gravity platforms, etc. For the soil-plate system, change in deflection due to consolidation process in clayey soil leads to time-dependent behaviour, which is of considerable interest in the foundation analysis. Initially, Terzaghi investigated the one-dimensional consolidation process of soft soil. Later, Biot (1941) extended the concept to consider the three-dimensional consolidation process of clayey soils. Further, Biot and Clingan (1942) studied the consolidation settlement of an elastic slab. Booker and Small studied the time-dependent behaviour of finite flexible circular raft on a deep homogenous porous elastic medium (Booker and Small 1984). Senjuntichai and Sapsathiarn (2006) dealt with circular plates on multi-layered poroelastic half space. Selvadurai (2007) provided an extensive review on contact problems between rigid plate and poroelasticity medium. Recent study includes Fang et al. (2014) which investigated the pavement response under moving traffic loads resting on multi-layered poroelastic medium, based on the theory proposed by Biot on homogenous poroelastic medium. Ai et al. (2014) analysed the time-dependent behaviour of plate of arbitrary shape and rigidity on layered saturated soil.

The research workers using analytical and semi-analytical methods have extensively studied the time-dependent behaviour of soil-foundation contact problems, which involves mathematical complexity. In case of plates, two-way bending occurs and therefore three-dimensional soil-foundation system is considered. As in soil-foundation interaction analysis, contact pressure determination is a crucial one. In order to obtain closest physically possible behaviour, simple mathematical relationship at the area of contact, one and two parameter models (also called as lumped parameter models) have already been developed. In the present paper, such a methodology has been used to model and understand the flexural response of square plates resting on viscoelastic medium exhibiting time-dependent behaviour.

2 Analysis

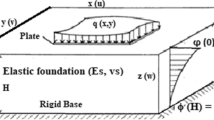
The viscoelastic behaviour of soil has been represented using Burgers model that consists of springs (k₁, k₂) and dashpots (η₁, η₂) interconnected by a tension membrane ‘T’, and the cross-sectional profile of a plate resting over it has been depicted in Fig. 1.

Fig. 1

Plate of viscoelastic foundation

The flexural response of a square plate of dimension B with thickness, h and flexural rigidity D subjected to uniform load intensity p, on viscoelastic foundation bed at any time, t is given by the equation below

$$D\nabla^{4} w\left( {x,y} \right) - T\nabla^{2} w\left( {x,y} \right) + k_{s} w\left( {x,y,t} \right) = p\left( {x,y} \right)$$

(1)

where B and h are width and thickness of the plate, respectively. D is flexural rigidity of plate; w, the transverse deflection of plate; (x, y, z), space coordinates; p, the applied load intensity; $\nabla$², the Laplace operator, and $\nabla$⁴ is the biharmonic operator. k_s can be derived from basic principles as

$$k_{s} = \frac{{k_{1} }}{{1 + \frac{{k_{1} }}{{\eta_{1} }}t + \frac{{k_{1} }}{{k_{2} }}\left[ {1 - \exp \left( { - \frac{{k_{2} }}{{\eta_{2} }}t} \right)} \right]}}$$

Equation (1) has been solved adopting proper boundary conditions in its non-dimensional form using the following non-dimensional parameters.

$$\begin{aligned} X & = \frac{x}{B},Y = \frac{y}{B},W = \frac{w}{B},D^{*} = \frac{D}{{k_{1} B^{4} }}, \\ k_{1}^{*} & = \frac{{k_{1} B^{4} }}{D},k_{2}^{*} = \frac{{k_{2} B^{4} }}{D},\eta_{1}^{*} = \frac{{\eta_{1} B^{4} }}{Dt}, \\ \eta_{2}^{*} & = \frac{{\eta_{2} B^{4} }}{Dt},T^{*} = \frac{T}{{k_{1} B^{2} }},p^{*} = \frac{p}{{k_{1} L}} \\ \end{aligned}$$

Using the above parameters, Eq. (1) in its non-dimensional form can be obtained as follows:

$$\nabla ^{4} W - \frac{{T^{*} }}{{D^{*} }}\nabla ^{2} W + W = p^{*} \left( {X,Y} \right)$$

(2)

Equation (2) governing the time-dependent response of plate has been solved using finite difference scheme. For any interior node (i, j), the above equation can be expressed in finite difference form as

$$\begin{aligned} & \frac{1}{{\Delta X^{4} }}\left( {20\,W_{i,j} - 8\left( {W_{i,j + 1} + W_{i,j - 1} + W_{i + 1,j} + W_{i - 1,j} } \right)} \right. \\ & \quad + 2\left( {W_{i + 1,j + 1} + W_{i + 1,j - 1} + W_{i - 1,j + 1} + W_{i - 1,j - 1} } \right) \\ & \quad + \left. {W_{i,j + 2} + W_{i,j - 2} + W_{i + 2,j} + W_{i - 2,j} } \right) + \frac{1}{{D^{*} }}W_{(i,j)} \\ & \quad - \frac{{T^{*} }}{{D^{*} }}\left[ {\frac{{W_{i - 1,j} - 2W_{i,j} + W_{i + 1,j} }}{{\Delta X^{2} }} + \frac{{W_{i,j - 1} - 2W_{i,j} + W_{i,j + 1} }}{{\Delta X^{2} }}} \right] = \frac{{p^{*} }}{{D^{*} }} \\ \end{aligned}$$

(3)

ΔX is the elemental size of plate chosen appropriately. For nodes lying other than interior, similar kind of equation can be derived using the following boundary conditions:

$${\text{At}}\;X = 0,\frac{\partial W}{\partial X} = 0,V_{x}^{*} = 0$$

(4)

$${\text{At}}\;Y = 0,\frac{\partial W}{\partial Y} = 0,\,V_{y}^{*} = 0$$

(5)

$${\text{At}}\;X = 1,M_{x}^{*} = 0;V_{x}^{*} + T_{p}^{*} \frac{\partial W}{\partial X} = 0$$

(6)

$${\text{At}}\;Y = 1,M_{y}^{*} = 0;V_{y}^{*} + T_{p}^{*} \frac{\partial W}{\partial Y} = 0$$

(7)

$${\text{At}}\;Y = 1, \, X = \, 1,\left( {2M_{xy}^{*} } \right) - \frac{3}{4}T_{p}^{*} W = 0$$

(8)

here

$$T_{p}^{*} = \frac{{T^{*} L^{2} }}{D}$$

where

$$M_{x}^{*} = - D^{*} \left( {\frac{{\partial^{2} W}}{{\partial X^{2} }} + \nu \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right)$$

$$M_{y}^{*} = - D^{*} \left( {\frac{{\partial^{2} W}}{{\partial Y^{2} }} + \nu \frac{{\partial^{2} W}}{{\partial X^{2} }}} \right)$$

$$V_{x}^{*} = \left( {Q_{x}^{*} - \frac{{\partial M_{xy}^{*} }}{\partial Y}} \right) = - D^{*} \left( {\frac{{\partial^{3} W}}{{\partial X^{3} }} + \left( {2 - \nu } \right)\frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }}} \right)$$

$$V_{y}^{*} = \left( {Q_{y}^{*} - \frac{{\partial M_{xy}^{*} }}{\partial X}} \right) = - D^{*} \left( {\frac{{\partial^{3} W}}{{\partial Y^{3} }} + \left( {2 - \nu } \right)\frac{{\partial^{3} W}}{{\partial Y\partial X^{2} }}} \right)$$

$$M_{xy}^{*} = - D^{*} \left( {1 - \nu } \right)\frac{{\partial^{2} W}}{\partial X\partial Y}$$

where V ^*_x and V ^*_y represent shear forces and M ^*_x , M ^*_y , the bending moments.

Thus, a system of simultaneous equations has been obtained. By solving these, the flexural response of plate at any time ‘t’ has been obtained in terms of its deflection using LU decomposition method, which has further been used to calculate bending moment in the plate.

3 Convergence Criterion and Range of Parametric Values

Due to symmetry, only quarter of the plate has been considered, and based on the above formulation a computer program has been written to obtain the response of plate. Using convergence criterion as in Eq. (9), the total number of elements along the lateral dimensions of the plate has been obtained as 21 × 21, considering beyond which less than 1% variation in the results has been observed.

$$\left| {\frac{{W_{(i,j)}^{\text{new}} - W_{(i,j)}^{\text{old}} }}{{W_{(i,j)}^{\text{new}} }}} \right| \times 100\% < \varepsilon_{s}$$

(9)

For every node, (i, j) new and old represent the present and previous iterations, respectively. ε_s is the tolerance error that has been considered 10⁻⁵ in the present analysis.

Relevant parameters have been adopted for analysis from available literature and have been presented below in Table 1. The parameters of Burgers model can be determined by the procedure laid by Dey and Basudhar (2012).

Table 1 Range of input parameter values

4 Results and Discussion

4.1 Validation

Before proceeding with the parametric study, the solution obtained with the present methodology has been validated with the closed-form solution obtained by Vallabhan et al. (1991). Response of plate was obtained with similar differential equation (as in Eq. 1), where the parameters k_s and T are defined as modulus of subgrade reaction and shear modulus of subsoil, respectively, and the corresponding values are given as 8141 lbs/ft³ (1279.77 kN/m³), as 177,285 lbs/ft² (8509.7 kPa). Other input parameters are as follows: L × B × h of the plate, respectively, as 48 ft (14.63 m), 24 ft (7.32 m), 0.5 ft (0.152 m), modulus of elasticity of plate (E) as 432,000,000 psf (2.1 × 107 kPa) with uniform load (p) of 500 psf (23.94 kPa) acting on the plate. Adopting boundary conditions as per Vallabhan et al. (1991), the comparison of results has been shown in Fig. 2 which shows close agreement, thus validating the present methodology.

Fig. 2

Validation of the proposed model

4.2 Retardation Time (t_d) and Non-dimensional Elapsed Time (t^′)

Retardation time, t_d, can be defined as the degree of rigidity of the viscoelastic bed. Figure 3 shows the elapsed time of viscoelastic foundation with the corresponding maximum deflection. Retardation time can be obtained by joining the initial portion of the curve with the asymptotic part, which has been obtained as 250 days in the present case.

Fig. 3

Variation of maximum normalized deflection of plate with time: determination of t_d

Retardation time, obtained as above, has been used to normalize the elapsed time, and the same has been represented in its standard form to obtain time for completion of 100% primary consolidation. Figure 4 shows the conventional curve and the procedure to obtain the non-dimensional elapsed time. For the present analysis, the time required for 100% consolidation has been obtained as 1.3, i.e. 325 days.

Fig. 4

Variation of maximum normalized deflection of plate with non-dimensional elapsed time: determination of time required for 100% degree of consolidation

4.3 Degree of Consolidation (U)

Burgers model is an idealization of primary and secondary consolidation phenomenon. Following the standard procedure, one can find out the time required for 100% primary consolidation. In order to obtain the consolidation characteristics of soil, Fig. 5 has been replotted depicting the variation of degree of consolidation (U) on y-axis with respect to non-dimensional elapsed time. The degree of consolidation can be obtained using Eq. (10), and the procedure to obtain the U (primary consolidation) has been shown in Fig. 5. Using this procedure, the corresponding time required to obtain 50% primary consolidation has been depicted.

Fig. 5

Variation of degree of consolidation with non-dimensional elapsed time

$$U = \left[ {\frac{{W|_{{t^{{\prime }} }} - W|_{{t^{{\prime }} = 0}} }}{{W|_{{t^{{\prime }} = t_{100}^{{\prime }} }} - W|_{{t^{{\prime }} = 0}} }}} \right] \times 100$$

(10)

where $t_{100}^{{\prime }}$ corresponds to non-dimensional elapsed time for completion of 100% primary consolidation.

4.4 Influence of Magnitude of Applied Load (P)

Influence of magnitude of applied load on the normalized maximum deflection with non-dimensional elapsed time (t^′) has been shown in Fig. 6 for the input parameters as mentioned in the figure. As the load increases from 100 to 250 kN/m², the magnitude of deflection increases and the same has been observed to be of 60% at t^′ = 5. Figure 7 shows a linear increase in normalized maximum bending moment of plate with the corresponding increase in load at t^′ = 1. It has been observed that for the same increase in load, the bending moment has been observed to increase by 60%.

Fig. 6

Influence of applied load with time: maximum normalized deflection

Fig. 7

Influence of applied load: maximum normalized bending moment

4.5 Influence of Flexural Rigidity of Plate (D)

Effect of flexural rigidity of plate on normalized maximum deflection has been shown in Fig. 8, and the variation with respect to non-dimensional elapsed time (t^′) has been depicted for input parameters as follows: p = 150 kN/m², k₁/k₂ = 10, η₁/η₂ = 10⁴ and T = 10MN. With the change in flexural rigidity of plate (D) from 2 × 10³ to 7 × 10⁴ kN-m, the percentage increase of maximum deflection of plate at t^′ = 5 has been observed to be 37.4%, and the corresponding reduction in maximum normalized bending moment has been obtained as 92.8% as shown in Fig. 9.

Fig. 8

Influence of flexural rigidity of plate with time: maximum normalized deflection

Fig. 9

Influence of flexural rigidity of plate: maximum normalized bending moment

4.6 Influence of Relative Magnitude of Elastic Coefficients of Burgers Model (k₁/k₂)

The influence of relative magnitude of elastic constants of Burgers model (k₁/k₂) has been depicted in Fig. 10, and the input parameters taken have also been mentioned in the figure. With the increase in ratio of k₁/k₂ from 0.5 to 100, the maximum deflection has been found to increase by about 73% at lower values of t^′. However, at larger values of normalized time, t^′, the effect of parameter k₁/k₂ has been found to be negligible. It has been observed that at lower k₁/k₂ values, the model almost behaves as a Maxwell model and at higher ratios, it behaves almost as an linear elastic spring with constant load over it.

Fig. 10

Influence of relative magnitudes of elastic constants of Burgers model (k₁/k₂) on normalized maximum deflection of plate

4.7 Influence of Relative Magnitude of Viscous Coefficients of Burgers Model (η₁/η₂)

The influence of relative magnitude of viscous coefficients of Burgers model (η₁/η₂), varying η₁/η₂ from 100 to 10⁵, with other input parameters taken as: p = 150 kN/m², T = 10 MN, k₁/k₂ = 10, D = 7 × 10⁴ kN-m, has been shown in Fig. 11. At lower ratio (η₁/η₂= 100) as the resistance offered by the soil reduces, higher deflections have been obtained. A difference of about 35% has been observed when η₁/η₂ increased by 1000 at t^′= 2.5, thereafter the change in normalized maximum deflection has been observed to be minimal with any increase in the parameter, η₁/η₂.

Fig. 11

Influence of relative magnitudes of viscous coefficient of Burgers model (η₁/η₂) on normalized maximum deflection of plate

4.8 Influence of Tension in Elastic Membrane (T)

The influence of tension membrane interconnected to provide continuity in Burgers model has been presented in Fig. 12 for typical input parameters. It has been observed that the percentage decrease of 45% in normalized maximum deflection has been found with increase in T from 5 to 15 MN. This signifies the influence of presence of tension membrane in reducing the deflection which can represent the pre-tensioned geosynthetic layer placed over the subgrade.

Fig. 12

Influence of tension in elastic membrane on normalized maximum deflection of plate

5 Conclusions

A simple mathematical model to analyse the time-dependent behaviour of a square plate making use of Burgers model has been presented. The equations governing the flexural response of plate along with the boundary conditions have been discussed. Detailed parametric study influencing the soil-foundation behaviour has been carried out, and the influence of various model parameters with time has been exclusively discussed.

With the proposed model, the variation of degree of consolidation with time can be directly correlated, and therefore, the time required to complete 100% primary consolidation in relation to soil-foundation system can be obtained through the analysis.

The effect of applied load on the foundation has been found to be significant. With the increase in applied load intensity from 100 to 250 kN/m², 60% increase in normalized maximum deflection has been observed for typical values of input parameters.

Flexural rigidity of plate has also been found to be a significant factor influencing the response of soil-foundation system. As D increases from 2 × 10³ to 7 × 10⁴ kN-m, 35% reduction in normalized deflection has been observed, while the corresponding increase in bending moment has been obtained as 92.8%.

It has been observed that the ratio of elastic coefficients (k₁/k₂) of Burgers model influences the response of plate significantly at its lower values of elapsed time. However, as with time, it has negligible effect on the response.

Smaller values of ratio of viscous coefficients (η₁/η₂) have been found to influence the deflection of plate significantly. Beyond η₁/η₂ = 1000, the influence has been found to be negligible.

With the increase of tension in the elastic membrane from 5 to 15 MN, the maximum normalized deflection at t^′= 5 has been observed to reduce by 45%. This tension membrane can be idealized as a pre-tensioned geosynthetic over soft soil, thus the poor subsoil condition can be improved with tension membrane over it.