Keywords

1 Introduction

For analysing the lifetime data, there are number of models available in the literature. Earlier, only the constant, increasing and decreasing hazard rates received serious consideration. But, in real-life problem, a situation does arise when the hazard rate is expected to be non-monotone, for example, human life. To model such problems, several non-monotone hazard rate distributions were introduced. Mudholkar and Srivastava [7], Xie and Lai [10], Gupta et al. [4] and Xie et al. [11] are notable research works related to the non-monotone hazard rate data.

There is a growing interest in the study of inverse bathtub hazard rates nowadays. A study of head and neck cancer data, [2] showed inverse bathtub hazard rates, in which the hazard rate initially increased, attained a maximum, and then decreased before it finally stabilized due to therapy. Log-normal, log-logistic, Burr Type XII, Burr Type III, log-Burr Type XII and the inverse Weibull distributions are some of the statistical distributions that show inverse bathtub hazard rates.

In the present study, we used a transformation called DUS transformation proposed by Kumar et al. [5]. If F(x) is the cdf of some baseline distribution, then the cdf G(x) of new distribution is given by,

$$\displaystyle \begin{aligned} G(x)=\frac{e^{F(x)}-1}{e-1}. \end{aligned} $$

Maurya et al. [6] introduced a new class of distribution by using the generalization of DUS transformation. The cdf of Generalized DUS (GDUS) transformation is

$$\displaystyle \begin{aligned} G(x)=\frac{e^{(F^{\alpha}(x))}-1}{e-1}, \end{aligned} $$

where F(x) be the cdf of some baseline distribution. In both these papers, they used exponential distribution as the baseline distribution.

Our main objective in this paper is to introduce a new class of distribution which includes all types of failure rates for suitable choice of parameter. By using GDUS transformation, the obtained distribution is expected to possess both monotone and non-monotone failure rates depending on the values of the parameter. The Weibull distribution has wide application in reliability and survival analysis. Depending on the shape parameter, Weibull models show different types of observed failures of components. Therefore here we consider Weibull distribution with parameters λ and k as the baseline distribution in GDUS transformation. The cdf and pdf of Weibull distribution are, respectively, \(G(x)=1-e^{-(\frac {x}{\lambda })^{k}}\) and \(g(x)=(\frac {k}{\lambda })(\frac {x}{\lambda })^{k-1}e^{-(\frac {x}{\lambda })^{k}},\) x > 0, λ, k > 0.

Using GDUS and Weibull distribution, the cdf and pdf of the new distribution, i.e., GDUS Weibull Distribution (GDUSWD) can be obtained as

$$\displaystyle \begin{aligned} F(x)=\frac{e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}-1}{e-1};\end{aligned} $$
(1)
$$\displaystyle \begin{aligned} f(x)=\frac{\alpha k x^{k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}}{\lambda^k (e-1)},x>0,~\alpha ,~\lambda,~ k>0. \end{aligned} $$
(2)

The hazard function of the distribution is,

$$\displaystyle \begin{aligned} h(x;\alpha,\lambda,k)=\frac{\alpha k x^{k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}}{\lambda^k\left(e-e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}\right)}. \end{aligned} $$
(3)

The paper deals with the selected topics as follows: In Sect. 2, we plot the pdf and hazard rates for different values of parameters of the GDUSWD. Various statistical characteristics of proposed distribution like moments, quantile function order statistic and Reńyi entropy are included in Sect. 3. The parametric estimation for the new distribution is discussed in Sect. 4. In Sect. 5 we illustrate the flexibility of the proposed model for a real data set by using AIC (Akaike information criterion) and BIC (Bayesian information criterion), and finally recapitulate the conclusions in Sect. 6.

2 Shape of the pdf and Hazard Function

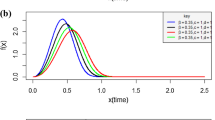
The distribution function may seem complicated, so we plot it to gain a better understanding of the nature of the distribution. Using Eq. (2), the plots of pdf for various values of the parameters α, λ and k are given in Fig. 1.

Fig. 1
figure 1

The probability density plot of GDUSWD. (Red) α = 0.5, k = 1.5, λ = 1.5; (blue) α = 1.5, k = 2, λ = 1.5; (green) α = 0.8, k = 2, λ = 1.5

Full size image

The term \(\eta (x)=\frac {-f'(x)}{f(x)}\), where f(x) is the density function of the distribution and f′(x) is the first derivative of f(x) with respect to x, is defined by Glaser [3] for the study of the shapes of the hazard rate. He stated the following theorem:

Theorem 1

  1. 1.

    If η ′(x) > 0 for all x > 0, then the distribution has increasing failure rate (IFR).

  2. 2.

    If η ′(x) < 0 for all x > 0, then the distribution has decreasing failure rate (DFR).

  3. 3.

    Suppose there exists x 0 > 0 such that η ′(x) > 0 for all x ∈ (0, x 0), η ′(x 0) = 0, and η ′(x) < 0 for all x > x 0 and 𝜖 =limx→0f(x) exists. Then if

    1. (i)

      𝜖 = 0, the distribution has inverse bathtub failure rate.

    2. (ii)

      𝜖 = ∞, the distribution has DFR.

In GDUSWD,

$$\displaystyle \begin{aligned} \eta(x)= \frac{-(k-1)}{x}+\frac{kx^{k-1}}{\lambda^{k}} \left[1-\frac{(\alpha-1)e^{-(\frac{x}{\lambda})^k}}{1-e^{-(\frac{x}{\lambda})^k}}-\alpha(1-e^{-(\frac{x}{\lambda})^k})^{\alpha-1}e^{-(\frac{x}{\lambda})^k} \right] \end{aligned} $$

and

$$\displaystyle \begin{aligned} \eta^{\prime}(x)=&\frac{k-1}{x^2}+\frac{k(k-1)x^{k-2}}{\lambda^k}\\ &-\frac{k(\alpha-1)}{\lambda^k}\left[ (1-e^{-(\frac{x}{\lambda})^k})e^{-(\frac{x}{\lambda})^k}\left((k-1)x^{k-2}-\frac{k}{\lambda^k}x^{2(k-1)}\right)\right.\\ &\quad \quad \quad \quad \quad \quad \left.- \frac{k}{\lambda^k}x^{2(k-1)}e^{-2(\frac{x}{\lambda})^k} \right]\\& -\frac{k\alpha}{\lambda^k}x^{k-1}e^{-(\frac{x}{\lambda})^k}(1-e^{-(\frac{x}{\lambda})^k})^{\alpha-2}\left[(\alpha-1)e^{-(\frac{x}{\lambda})^k}+(1-e^{-(\frac{x}{\lambda})^k}) \right].{} \end{aligned} $$
(4)

The obtained expression of η ′(x) is too complicated, so we have used the software MATHEMATICA for checking the conditions mentioned in Theorem 1. Here we have observed that

  • When α ≤ 0.5, we have η ′(x) < 0 for all x > 0, hence the distribution has DFR

  • When α ≥ 1, we have η ′(x) > 0 for all x > 0, hence the distribution has IFR

  • When 0.5 < α < 1, there exists a x 0 such that η ′(x) > 0 when x ∈ (0, x 0), η ′(x 0) = 0 and η ′(x) < 0 for all x > x 0, where x 0 depends on the value of α, λ and k.

From Eq. (2), we can easily verify that limx→0f(x) = 0, hence the distribution has inverse bathtub shaped failure rate. Figure 2 shows the different shapes of hazard rates.

Fig. 2
figure 2

The hazard rate plots of GDUSWD. (a) (Blue) α = 0.3, k = 2, λ = 0.1, (red) α = 0.4, k = 2, λ = 0.3. (b) (Blue) α = 0.8, k = 2, λ = 4, (red) α = 0.6, k = 2, λ = 3. (c) (Green) α = 1.5, k = 2, λ = 1.5, (blue) α = 2, k = 2, λ = 1.5

Full size image

3 Some Analytical Characteristics

Different statistical characteristics like moments, quantile function, order statistic and Reńyi entropy of our proposed distribution are discussed below.

3.1 Moments

The moments are used to understand the various characteristics of the proposed distribution. The rth raw moment of the GDUSWD is

$$\displaystyle \begin{aligned} E(X^{r})=\frac{\alpha k}{\lambda^{k}(e-1)}\int_{0}^{\infty} x^{r+k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}dx \end{aligned} $$

Expanding the exponential term \(e^{x}=\sum _{i=0}^{\infty }\frac {x^{i}}{i!}\), we get

$$\displaystyle \begin{aligned} E(X^{r})=&{}\frac{\alpha k}{\lambda^{k}(e-1)}\int_{0}^{\infty} x^{r+k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}\sum_{\ell=0}^{\infty}\frac{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha \ell}}{\ell!}dx.\end{aligned} $$

Here the summation is absolutely convergent, we can interchange the summation and integral.

$$\displaystyle \begin{aligned} E(X^{r})=&{}\frac{\alpha k}{\lambda^{k}(e-1)}\sum_{\ell=0}^{\infty}\frac{1}{\ell!}\int_{0}^{\infty} x^{r+k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha \ell}dx.\end{aligned} $$

Using the expansion of series, \((1-y)^{b}=\sum _{i=0}^{\infty }(-1)^{i} {b \choose i}y^{i}\) and simplifying

$$\displaystyle \begin{aligned} E(X^{r})=\frac{\alpha}{\lambda^{k}(e-1)}\sum_{\ell=0}^{\infty}\sum_{m=0}^{\infty}\frac{(-1)^{m}}{\ell !}{\alpha \ell+\alpha-1 \choose m} \frac{\varGamma (\frac{r}{k}+1)} {(\frac{m+1}{\lambda^{k}})^{\frac{r}{k}+1}}.\end{aligned} $$

This expression of rth raw moment gives variance and other higher order central moments.

3.2 Quantile Function

The pth quantile function Q(p) of our proposed distribution is obtained from the equation,

$$\displaystyle \begin{aligned} F(Q(p)) = p\end{aligned}$$
$$\displaystyle \begin{aligned} Q(p)=\lambda \left[-log(1-log(1+p(e-1))^{\frac{1}{\alpha}})\right]^{\frac{1}{k}}. \end{aligned} $$
(5)

3.3 Order Statistic

Order statistics are sample values placed in ascending order. The study of order statistics deals with the applications of these ordered values and their functions. Let X 1, X 2, …, X n be a random sample of size n from the GDUSWD distribution and X (1), X (2), …, X (n) denote the corresponding order statistics. The pdf and cdf of the rth order statistics f r(x) and F r(x) are given by

$$\displaystyle \begin{aligned} f_{r}(x)=\frac{n!}{(r-1)!(n-r)!}F^{r-1}(x)[1-F(x)]^{n-r}f(x)\end{aligned}$$

and

$$\displaystyle \begin{aligned} F_{r}(x)=\sum_{j=r}^{n}{n \choose j}F^{j}(x)[1-F(x)]^{n-j}.\end{aligned}$$

The pdf f r(x) and cdf F r(x) of rth order statistic of our proposed distribution are obtained by using Eqs. (1) and (2) as,

$$\displaystyle \begin{aligned} f_{r}(x)=&\frac{n!}{(r-1)!(n-r)!}\left(\frac{e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}-1}{e-1}\right)^{r-1} \left(\frac{e-e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}}{e-1}\right)^{n-r}\\&\frac{\alpha (\frac{k}{\lambda})(\frac{x}{\lambda})^{k-1}e^{-(\frac{x}{\lambda})^{k}}\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha -1}e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}}{e-1}{} \end{aligned} $$
(6)

and

$$\displaystyle \begin{aligned} F_{r}(x)=\sum_{j=r}^{n}{n \choose j}\left(\frac{e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}-1}{e-1}\right)^{j}\left(\frac{e-e^{\left(1-e^{-(\frac{x}{\lambda})^{k}}\right)^{\alpha}}}{e-1}\right)^{n-j}. \end{aligned} $$
(7)

The pdf of smallest and largest order statistics X (1) and X (n) is obtained by putting r = 1 and r = n, respectively, in Eq. (6). The cdf of X (1) and X (n) is obtained by putting r = 1 and r = n, respectively, in Eq. (7).

3.4 Entropy

Entropy is interpreted as the degree of disorder or randomness in the system. Reńyi entropy [8] is one of the well-known entropy measures. If random variable X has the pdf f(x), then the Reńyi entropy is defined as,

$$\displaystyle \begin{aligned} \mathcal{J}_{R}(\gamma)=\frac{1}{1-\gamma}log\left[\int f^\gamma(x)dx \right], \end{aligned} $$
(8)

where γ > 0 and γ ≠ 1. From Eq. (2), we get,

$$\displaystyle \begin{aligned} \int_{0}^{\infty} f^\gamma(x)dx=\int_{0}^{\infty}\left(\frac{\alpha k}{\lambda^{k}(e-1)}\right)^{\gamma}x^{\gamma (k-1)}e^{-\gamma(\frac{x}{\lambda})^{k}}\left(1-e^{(\frac{x}{\lambda})^{k}}\right)^{\gamma(\alpha-1)}e^{\gamma \left(1-e^{(\frac{x}{\lambda})^{k}}\right)^{\alpha}}\end{aligned}$$

after some algebra, which is used in Sect. 3.1

$$\displaystyle \begin{aligned} \int_{0}^{\infty} f^\gamma(x)dx=\frac{\alpha^{\gamma}k^{\gamma-1}}{\left(\lambda^{k}\right)^{\gamma-1}\left(e-1\right)^{\gamma}}\sum_{i=0}^{\infty}\sum_{j=0}^{\infty}\frac{\gamma^{i}}{i!}{\alpha i+\gamma \alpha-\gamma \choose j}\frac{(-1)^{j}}{(\gamma+j)}.\end{aligned}$$

With this, Eq. (7) becomes,

$$\displaystyle \begin{aligned} \mathcal{J}_{R}(\gamma)&=\frac{\gamma}{1-\gamma}log\left(\frac{\alpha}{e-1}\right)-log\left(\frac{k}{\lambda^k}\right)\\ &\quad +\frac{1}{1-\gamma}log\left[\sum_{i=0}^{\infty}\sum_{j=0}^{\infty}\frac{\gamma^{i}}{i!}{\alpha i+\gamma \alpha-\gamma \choose j}\frac{(-1)^{j}}{(\gamma+j)}\right]. \end{aligned} $$
(9)

4 Estimation

Maximizing the logarithm of likelihood function is the most common method for finding the estimates—called MLE (Maximum Likelihood Estimates)—of the parameters involved in the given distribution. In this section, we use this method for obtaining the maximum likelihood estimates of the parameters α, λ and k of the proposed distribution. The log-likelihood function is,

$$\displaystyle \begin{aligned} log~L(x;\lambda)=\prod_{i=1}^{n}f(x_{i};\lambda)\end{aligned} $$
$$\displaystyle \begin{aligned} log~L(x;\alpha, \lambda, k)=& n~ log\alpha +n~ log\left(\frac{k}{\lambda}\right)+n(k-1) log\lambda+(k-1)\sum_{i=1}^{n}log x_{i}\\&-\sum_{i=1}^{n}\left(\frac{x_{i}}{\lambda}\right)^{k}+(\alpha-1)\sum_{i=1}^{n}log(1-e^{-(\frac{x_{i}}{\lambda})^{k}})\\&+\sum_{i=1}^{n}\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right)^{\alpha}-n~log(e-1). \end{aligned} $$

Differentiating this function with respect to the parameters we get,

$$\displaystyle \begin{aligned} \frac{\partial log~L}{\partial \alpha}=\frac{n}{\alpha}+\sum_{i=1}^{n}log\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right)+\sum_{i=1}^{n}\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right)^{\alpha}log\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right),\end{aligned} $$
$$\displaystyle \begin{aligned} \frac{\partial log~L}{\partial \lambda}&=\frac{-n}{\lambda}+\frac{n(k-1)}{\lambda}+\frac{k\sum_{i=1}^{n}x_{i}^{k}}{\lambda^{k+1}}-(\alpha-1)\sum_{i=1}^{n}\frac{e^{-(\frac{x_{i}}{\lambda})^{k}}}{1-e^{-(\frac{x_{i}}{\lambda})^{k}}}\left(\frac{x_{i}}{\lambda}\right)^{k}\frac{k}{\lambda} \\ &\quad -\alpha \sum_{i=1}^{n}\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right)^{\alpha-1}e^{-(\frac{x_{i}}{\lambda})^{k}}\left(\frac{x_{i}}{\lambda}\right)^{k}\frac{k}{\lambda}, \end{aligned} $$

and

$$\displaystyle \begin{aligned} \frac{\partial log~L}{\partial k}=&\frac{n}{k}+n~log\lambda+\sum_{i=1}^{n}log(x_{i})-\sum_{i=1}^{n}\left(\frac{x_{i}}{\lambda}\right)^{k}log\left(\frac{x_{i}}{\lambda}\right)\\&+(\alpha-1) \sum_{i=1}^{n}\frac{e^{-(\frac{x_{i}}{\lambda})^{k}}}{1-e^{-(\frac{x_{i}}{\lambda})^{k}}}\left(\frac{x_{i}}{\lambda}\right)^{k}log\left(\frac{x_{i}}{\lambda}\right)\\&+ \alpha \sum_{i=1}^{n}\left(1-e^{-(\frac{x_{i}}{\lambda})^{k}}\right)^{\alpha-1}e^{-(\frac{x_{i}}{\lambda})^{k}}\left(\frac{x_{i}}{\lambda}\right)^{k}log\left(\frac{x_{i}}{\lambda}\right). \end{aligned} $$

Equating these partial derivatives to zero yields three non-linear equations, and their solutions provide the maximum likelihood estimate of the parameters α, λ and k. Newton–Raphson method can be used to solve these equations with the help of the available statistical packages.

5 Application

In this section, we have checked the flexibility of the proposed distribution and compared it with some well-known distributions namely, Inv. Lindley, Inv. Exponential, Gn. Inv. Lindley, Inv. Weibull, Inv. Gamma, Inv. Gaussian and Gn. Inv. Exponential, see Vikas et al. [9]. For the purpose of comparison, we have considered a set of real data of flood levels [1],

  • 0.654, 0.613, 0.315, 0.449, 0.297, 0.402, 0.379, 0.423, 0.379, 0.324,

  • 0.296, 0.740, 0.418, 0.412, 0.494, 0.416, 0.338, 0.392, 0.484, 0.265.

Many authors have used this data for checking the flexibility of their proposed distributions. We have used AIC (Akaike information criterion) and BIC (Bayesian information criterion) for comparing our model with other models. AIC and BIC are defined as,

$$\displaystyle \begin{aligned} {\mathrm{AIC}}=2 \times k-2\times Log~L,\end{aligned}$$

and

$$\displaystyle \begin{aligned} {\mathrm{BIC}}=k\times Log(n)-2\times Log~L,\end{aligned}$$

where n is the sample size, k is the number of parameters and L is the maximum value of the likelihood function for the considered distribution. A minimum value of AIC and BIC is a sign of better fit of distributions.

From Table 1, it can be seen that the proposed distribution gives the lowest AIC and BIC values. So we can conclude that GDUSWD provides the best fit for the data set compared to the other distributions given in this study.

Table 1 AIC, BIC and ranks [1(best) to 8( worst)] of the fitted models
Full size table

6 Conclusion

In the present study, we have introduced a new lifetime distribution exhibiting increasing, decreasing and inverse bathtub failure rates. We then derived its moments, quantile function, order statistic and Reńyi entropy. We have considered a real dataset and compared our proposed distribution with some other well-known distributions. It is seen that among the distributions considered, the one proposed here fits best with the data. Thus, we can say that the GDUSWD is more flexible compared to the distributions mentioned in this study.