Keywords

1 Introduction

Flexible AC transmission system (FACTS) devices are well known for their ability to improve the power system dynamic and transient performances. FACTS devices vary the admittance between the two points in a transmission network and hence dynamically control the power flow through the transmission network. With the advent of the Voltage Source Converters (VSC) static synchronous compensator (STATCOM) is made possible. STATCOM is a controllable synchronous voltage source and is increasingly being used in power systems to control the real-time power flow and for rotor oscillation damping. The STATCOM is similar to the static var compensator in a way that it provides shunt compensation, but STATCOM uses a voltage source converter instead of shunt capacitors and reactors as in the case of static var compensator [1–5]. STATCOM provides a large number of performance benefits. The control circuit in the STATCOM has auxiliary signals that can be used for damping enhancement of a power system in terms of its rotor angular stability [3–5]. Many control strategies for dynamic performance improvement of power system using STATCOM control have been reported in the literature. A rule-based control strategy for STATCOM is proposed in [4]. The multivariable sampled regulator was designed for STATCOM to control the rotor angle oscillations in [5]. Some control techniques for STATCOM control that show robust performance have also been studied [6–8]. In [8] robust control of SVC and STATCOM using the H∞ design approach is presented. Designing robust controllers using H∞ approach is a tedious task. A simple loop-shaping technique, that produces a robust controller with fixed parameters, has been reported in [6, 7]. The design of robust controllers using evolutionary optimization techniques for damping enhancement of power system oscillations by the simultaneous stabilization technique has been presented in [9, 10]. Simultaneous stabilization is known to be a very challenging problem and no general systematic solution is obtainable. Iterative optimization techniques are proven to be the best alternatives in the absence of analytic solutions. A single set of PSS parameters can be found using a simultaneous stabilization method to guarantee the stabilization of the power system over the wide range of operations as reported in [9, 10].

In this paper, robust controllers were designed by the graphical loop-shaping technique and simultaneous stabilization approach using PSO for a single machine infinite system installed with STATCOM. In the graphical loop- shaping technique changes in the system loading conditions were included as a structured uncertainty model. In the simultaneous stabilization technique, the power system operating at different operating points is considered as a finite set of system transfer functions. The problem of selecting a fixed parameter robust controller is transformed into a simple optimization problem which is solved by Particle Swarm Optimization (PSO) and an eigen value-based objective function. The effectiveness of both methods is compared through nonlinear simulations of the power system installed with STATCOM.

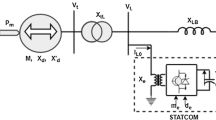
2 The Power System Model Installed with STATCOM

Figure 1 shows a SMIB with a STATCOM installed in the middle of the transmission line. The generator is represented in terms of two electromechanical swing equations and an internal voltage equation. The dynamic model of the power system installed with STATCOM at the mid-point of the transmission line can be represented by a set of nonlinear equations given by (1) [11]. In (1), δ and ω are the rotor angle and generator speed whereas Efd and eq′ are the field voltage and internal voltage, respectively.

Fig. 1
figure 1

SMIB power system with STATCOM

Full size image
$$ \begin{aligned} \dot{\delta } & = \omega - \omega_{{o}} \\ \dot{\omega } & = - \frac{ 1}{M}\left[ {P_{m} - P_{e} - D\left( {\omega - \omega_{o} } \right)} \right] \\ \dot{e}_{q}^{'} & = \frac{ 1}{{T_{\text{do}}^{'} }}\left[ {E_{\text{fd}} - e_{q} } \right] \\ \dot{E}_{\text{fd}} & = - \frac{ 1}{{T_{A} }}\left( {E_{\text{fd}} - E_{\text{fdo}} } \right) + \frac{{K_{A} }}{{T_{A} }}\left( {V_{\text{to}} - V_{\text{t}} } \right) \\ \end{aligned} $$
(1)

The STATCOM is connected to the transmission line through a step-down transformer (SDT) with a leakage reactance equal to XSDT. A three-phase GTO-based voltage source converter, and a D.C. capacitor is an inherent part of the STATCOM system. The dynamic relationship that exists between STATCOM current (Idc) and the capacitor voltage (Vdc) can be represented by (2),

$$ \frac{{{\text{d}}V_{\text{dc}} }}{{{\text{d}}t}} = \frac{{I_{\text{dc}} }}{{C_{\text{dc}} }} = \frac{m}{{C_{\text{dc}} }}\left( {I_{\text{Lod}} \cos\uppsi + I_{\text{Loq}} \sin\uppsi} \right) $$
(2)

The direct and quadrature axes components of STATCOM current ILo are represented as ILod and ILoq. The output voltage phasor is given by (3),

$$ \bar{V}_{o} = mV_{\text{dc}} \angle \;\uppsi $$
(3)

In (2) and (3), ψ is the phase and m is the modulation index.

If the state and control vectors are taken as,

$$ \left[ {\Delta \delta \, \Delta \omega \, \Delta e^{\prime}_{q} \, \Delta E_{\text{fd}} \;\Delta V_{\text{dc}} } \right]^{\text{T}} \& \left[ {\Delta m \, \Delta\uppsi} \right]^{\text{T}} $$

Then the nonlinear state equations given by (1) and (2) for the SMIB with STATCOM can be represented as in (4),

$$ \dot{x} = f(x,u) .$$
(4)

3 The Design of Robust Controller for STATCOM Using Graphical Loop-Shaping Technique

The design of robust controller for the SMIB with STATCOM, begins by linearizing the nonlinear model of (4), around a nominal operating point

$$ \begin{aligned} \dot{x} & = Ax + Bu \\ y & = Hx \\ \end{aligned} $$
(5)

In the state space model of (5), control u is the modulation index m which is a measure of the STATCOM voltage magnitude. The nominal plant transfer function is

$$ P = {\text{H}}\left[ {sI - A} \right]^{ - 1} B $$
(6)

Perturbations in the plant operating points is incorporated by a structured uncertainty model as

$$ \tilde{P} = (1 + DW_{2} )P $$
(7)

Equation (7) is the multiplicative uncertainty model where, W2 is a fixed stable transfer function, D is a variable transfer function satisfying \( \left\| D \right\|_{\infty } < 1 \). If \( \left\| D \right\|_{\infty } < 1 \) then

$$ \left| {\frac{{\tilde{P}(j\omega )}}{P(j\omega )} - 1} \right| \le \left| {W_{2} (j\omega )} \right|,\forall \omega $$
(8)

Therefore, \( \left| {W_{2} (j\omega )} \right| \) is the uncertainty profile and in the frequency domain is the upper boundary of all the normalized plant transfer functions away from 1. For a controller function C in series with the plant P, the robustness criteria are

  1. 1.

    The nominal performance measure is \( \left\| {W_{1} S} \right\|_{\infty } < 1 \)

  2. 2.

    C provides robust stability if

    $$ \left\| {W_{2} T} \right\|_{\infty } < 1 $$
    (9)
  3. 3.

    Necessary and sufficient condition for robust nominal and robust performance is \( \left\| {\left| {W_{1} S} \right| + \left| {W_{2} T} \right|} \right\|_{\infty } < 1 .\)

It is to be noted here that W1 is a real, rational, stable and minimum phase function. T is the input-output transfer function, S is the complement of the sensitivity function, and is given by

$$ T = 1 - S = \frac{1}{1 + L} = \frac{1}{1 + PC} $$
(10)

Loop-shaping is a graphical method to design a robust controller C satisfying performance criteria and robust stability criteria as given in (9). The method relies on graphically constructing the open-loop transfer function, L = PC to satisfy the robust performance criterion approximately, and then finally the robust controller is obtained from the relationship C = L/P. The constraints of this graphical method are internal stability of the plants and properness of C. Open-loop transfer function L should be constructed such that PC should not have any pole zero cancellation. An essential condition for robustness is that either or both |W1|, |W2| must be less than 1 [7]. For a monotonically decreasing function W1, it can be shown that at low frequency the open-loop transfer function L should satisfy

$$ \left| L \right| > \frac{{\left| {W_{1} } \right|}}{{1 - \left| {W_{2} } \right|}} $$
(11)

while for high frequency

$$ \left| L \right| < \frac{{1 - \left| {W_{1} } \right|}}{{\left| {W_{2} } \right|}} \approx \frac{1}{{\left| {W_{2} } \right|}}. $$
(12)

4 The Particle Swarm Optimization (PSO)

4.1 Introduction to PSO

The PSO is a heuristic optimization algorithm based on the social behavior of bird flocking and fish schooling and it was developed by Abdel-Magid et al. [9]. Similar to other evolutionary algorithms like Genetic Algorithms, PSO is also an optimization technique based on population. Unlike GA no operations in PSO are inspired by evolution to find new generations of candidate solutions, but instead, PSO depends on the exchange of information between individuals known as particles of the population [12–14]. The particles in the swarm update their own velocity and position according to the following equations given by (13) and (14), respectively.

$$ V_{i} = QV_{i} + K_{1} {\text{rand}}_{1} ( \, )(X_{{{\text{pbest}}}} - X_{i} ) + K_{2} {\text{rand}}_{2} ( \, )(X_{{{\text{gbest}}}} - X_{i} ) $$
(13)
$$ X = X_{i} + V_{i} $$
(14)

In (13) K1 and K2 are two positive constants, rand1 ( ) and rand2 ( ) are random numbers in the range [0, 1], and Q is the inertia weight. Xi represents the position of the ith particle in the swarm and Vi is particle velocity in Eq. (14).

4.2 PSO Flow Chart

The PSO flow chart used in this paper is shown in Fig. 2.

Fig. 2
figure 2

Flow chart of PSO

Full size image

4.3 Simultaneous Tuning Using PSO

In this approach, the controller structure is pre-selected as two lead-lag blocks and a washout given by

$$ C(s) = K\left( {\frac{{sT_{w} }}{{1 + sT_{w} }}} \right)\left( {\frac{{1 + sT_{1} }}{{1 + sT_{2} }}} \right)\left( {\frac{{1 + sT_{3} }}{{1 + sT_{4} }}} \right) $$
(15)

where K is the stabilizer gain, T1, T2, T3, and T4 are stabilizer time constants and Tw is the washout time constant. In this controller structure, Tw is usually a pre-selected value. The constraints on the values of K and the time constants are given by

$$ \begin{aligned} K^{\hbox{min} } \le K \le K^{\hbox{max} } \hfill \\ T_{1}^{\hbox{min} } \le T_{1} \le T_{1}^{\hbox{max} } \hfill \\ T_{2}^{\hbox{min} } \le T_{2} \le T_{2}^{\hbox{max} } \hfill \\ T_{3}^{\hbox{min} } \le T_{3} \le T_{3}^{\hbox{max} } \hfill \\ T_{4}^{\hbox{min} } \le T_{4} \le T_{4}^{\hbox{max} } \hfill \\ \end{aligned} $$
(16)

The objective function J to be minimized in the PSO algorithm is an eigen value-based objective function chosen to place the real part of the complex eigen values of the mechanical modes at a pre-determined location in the s-plane for all the operating points considered. The performance index is expressed as

$$ J = \sum\limits_{i = 1}^{N} {\left( {\sigma_{s} - \sigma_{i} } \right)^{2} } $$
(17)

where \( \sigma_{s} \) and \( \sigma_{i} \) are pre-selected value and real part of eigen value of the mechanical mode for the ith plant respectively and N is the number of operating points considered during the design.

5 Implementation of Robust Controllers

5.1 Graphical Procedure

For the SMIB with STATCOM of Fig. 1, the input is chosen as the modulation index m whereas changes in angular speed, Δω of generator is chosen as the system output. For the chosen nominal operation, the nominal plant is given by (18)

$$ P = \frac{{0.2104s^{2} (s + 100.827)(s - 0.234)}}{{\left( {s + 99.17} \right)(s + 1.10)(s + 0.05)(s^{2} + 0.68s + 21.63)}} $$
(18)

Output power ranges between 0.4 and 1.4 pu and the range of power factor considered is 0.8 lagging to 0.8 leading. The uncertainty profile is fitted to the weight function, W2 given by

$$ W_{2} (s) = \frac{{0.9s^{2} + 15s + 27}}{{s^{2} + 5s + 31}} $$
(19)

W1(s) is chosen as a Butterworth filter that satisfies all the properties of the uncertainty profile and is given by (20)

$$ W_{1} (s) = \frac{{K_{d} f_{c}^{2} }}{{s^{3} + 2s^{2} f_{c} + 2sf_{c}^{2} + f_{c}^{3} }} $$
(20)

In (20) Kd = 0.01 and fc = 0.1 are chosen, and L is given by (21) and C by (22)

$$ \begin{aligned} L & = \frac{{5.173s^{2} (s + 100.827)(s - 0.234)(s + 1)(s + 1.094)}}{{\left( {s + 99.17} \right)(s + 1.10)(s + 0.05)(s^{2} + 0.68s + 21.63)}} \\ & \quad \times \, \frac{(s + 0.0476)(s + 0.001)(s + 99.174)}{(s + 10)(s + 0.1)(s + 0.01)(s + 0.03)(s + 0.05)} \\ \end{aligned} $$
(21)
$$ C = \frac{24.583(s + 1)(s + 1.094)(s + 0.0476)(s + 0.001)(s + 99.174)}{(s + 10)(s + 0.1)(s + 0.01)(s + 0.03)(s + 0.05)} $$
(22)

The bode plots for W1, W2, and L, which were used to find this robust controller, is given in Fig. 3a. The open-loop function L given by (21) is chosen to satisfy the boundaries set by (11–12). Figure 4 shows the plots for nominal and robust performance criteria. As evident from Fig. 3b, the nominal performance measure W1S is well-satisfied whereas the combined robust stability and performance measure has a slight peak.

Fig. 3
figure 3

a Graphical loop-shaping plots relating W1, W2, and L. b The robust performance criteria

Full size image
Fig. 4
figure 4

a Convergence rate of the objective function. b Pole placement for four different operating points

Full size image

5.2 Simultaneous Tuning Using PSO

The proposed approach is implemented on the power system shown in Fig. 1. The PSO algorithm was used to minimize the objective function given by (17) where \( \sigma_{s} \) was chosen as −0.6 as it gives the best damping properties for the power system. The PSO algorithm converged to give the following settings for the lead-lag controller blocks: K = 27.4, T1 = T3 = 0.0120, T2 = T4 = 0.0222. The washout time constant Tw was selected as 2 s.

The convergence rate of the objective function J is shown in Fig. 4a. It is evident from Fig. 4a that the objective function reaches the minimum value very fast. Figure 4b shows the placement of poles for four different operating points. It can be observed clearly that the real parts of the poles (\( \sigma_{i} \)) are exactly placed as desired at −0.6 for the four operating points considered during the design. A comparison of the simulation results with the graphical loop-shaping and simultaneous tuning using PSO is given in Fig. 5.

Fig. 5
figure 5

Comparison of rotor angle changes upon a 50% disturbance on torque input (solid line is for loop-shaping technique and dotted line for simultaneous tuning using PSO)

Full size image

The rotor angle response for the four loading conditions are presented in Fig. 5. It can be deduced that both the graphical loop-shaping technique and simultaneous tuning using PSO produce robust controllers that give almost identically good transient performance.

6 Conclusions

In this paper, a comparative study was performed for designing robust STATCOM controllers by the graphical loop-shaping method and simultaneous tuning using Particle Swarm Optimization (PSO). Uncertainties in system loading conditions were considered for the purpose of design. However, the methods can also be applied with equal ease to include the uncertainties in the generator parameter variations. Both the graphical loop-shaping method and the simultaneous tuning method give almost similar transient responses. It was observed that the transient response for light conditions was found to be much better in the case of simultaneous tuning when compared to the graphical loop-shaping method. It is to be noted that compared to simultaneous tuning using PSO, the graphical loop-shaping method is more mathematically involved and requires graphical construction of weight function W2 which is a bit time-consuming procedure for the amateur designer.