A Simplified Nonlinear Analysis Procedure for the Flexible Risers in Subjected to Combined Loading Effects

Abstract

A dynamic analysis of flexible risers in large-scale domain remains the offshore industry’s most challenging problems. The cross section of flexible risers, consisting of multiple metallic and plastic layers, experiences inter-layer slippage during cyclic bending. This results in nonlinear and hysteretic bending behavior with rapid dissipation of energy. For the dynamic analysis for flexible risers in the large scale domain, this study replaces all layers of risers with simple beam elements with a nonlinear beam model. This simplified beam model traces the curvature to bending moment relation and captures the variation of stiffness due to the onset of slippage. The suggested methods formulate both the change of configuration due to large deflection and contact between risers and seabed, therefore more realistic and effective analysis can be achieved. In the current study, the details of the analysis method are described. Main formulation methods of the total Lagrangian framework and the interaction between risers and seabed are described as well as the nonlinear bending model for flexible risers. The validity of the developed method is examined through some case studies, and the results show how the bending nonlinearity of flexible risers affects the overall behavior of riser systems during its operation.

1 Introduction

Flexible risers are widely used pipelines in the offshore industry to transfer oil products from the well to the platform. The metallic layers of flexible risers are wounding the internal bores with helical shape, in which the interlayer slippage between the layers maximizes the bending flexibility in critical locations such as touch down zone. Recent developments of high-tensile wires further contribute to the extension of service life and to the prevention of radial buckling. Although these advantages, the design of flexible risers requires uncertain and time-consuming from the early development phases. The helical wires inside tensile armor wires generally exert cyclic stick-slippage phenomena, therefore the cross-section of flexible risers undergo rapid energy dissipation during bending. This makes it hard to predict the dynamic behavior of flexible risers both in the local-scale and large-scale domain.

Many studies have dealt with the dynamic analysis of flexible risers. Feret and Bournazel (1987) formulated the axial and radial displacements of the riser subjected to tension and pressure loads. They derived an explicit form for the stress and displacement fields for each layer, in which the overall fields are expressed by several cross-sectional variables. In their works, this equation provides a constitutive matrix so that the static problem of small-scale flexible risers can be linearized. Witz (1996) examined the effectiveness of theoretical approaches through some experiments on the internal diameter of 10-in. flexible risers. The validation against the results obtained by theoretical approaches showed that theoretical approaches provide a proper model for flexible risers. Feret et al. (1995) assumed that movements of helical wires always follows the torus surface of their contact surface. Accordingly, the normal stress of wires is expressed as a differential form using the Darboux frame. With the derived stress field, the authors accomplished to take into account the interlayer slippage for the moment calculation. Kebadze and Kraincanic (1999) presented a similar approach in which the deformed helical wires are assumed to follow the helical path. He treated tensile armor layers as a homogeneous tube, presuming that all helical wires are contacted with surrounding layers until a certain threshold. The authors noted that each wire loses its friction after a critical curvature, so the nonlinear bending hysteresis curve can be obtained by deriving the equilibrium of sliding force and friction.

The dynamic analysis for flexible risers has been another interest among many researchers. Fylling and Bech (1991) investigated the effect of the nonlinear bending on the dynamic behavior of flexible risers. They found that friction along the contact surface of helical wires dominates curvature responses. Dib et al. (2013) employed a nonlinear dynamic substructuring technique to the dynamic analysis of flexible risers. The presented method quickly estimates the responses of all riser segments based on the several deformation modes and the coordinate transformation between local and large scale model.

Previous researchers have suggested various methods in the prediction of dynamic responses of flexible risers. However, in the previous studies, many simplifications are made in the modeling of flexible risers and the detailed effects of the interlayer slippage have been overlooked. In view of this, some improvements are still required to achieve an accurate dynamic simulation of flexible risers.

In order to address the current issue, a new dynamic analysis method for flexible risers, referred to as an OPFLEX, are being developed. The purpose of this development is to take into account the interaction between helical wires and surrounding layers in the global dynamic analysis, employing an accurate nonlinear bending model in the modeling of riser systems. The nonlinear model of each element captures the onset of the slippage during dynamic analysis, therefore the bending behavior of flexible risers can be simulated in the large-scale domain. The element of riser models is formulated based on the Euler beam model. The deflection of this model is basically solved under the total Lagrangian framework with a high order strain and stress basis, therefore both the large deflection and nonlinear bending effects of flexible risers can be incorporated into the solver. This study, as a first phase of the developments, aims at the validation of the presented dynamic analysis solver and the investigation of the influence of the interlayer slippage of flexible risers on the dynamic behavior of riser configurations.

The present study unfolds as follows. Firstly, the details of the formulation of the dynamic analysis solver will be introduced. The static and dynamic analysis method based on the total Lagrangian framework and time marching scheme estimates the structural behavior of riser structures subjected to various load conditions. Then, the theoretical approach for flexible risers and its implementation on Euler beam models are introduced. Finally, the influence of dynamic responses of flexible risers will be investigated through the comparative study.

2 Detailed Formulation of Riser Dynamic Analysis

2.1 Total Lagrangian Formulation for Euler Beam

The dynamic analysis of risers generally requires a large displacement analysis due to its geometric characteristics. In the large-scale domain, the vibration of risers can be predicted with the catenary equations, but this neglects the bending stiffness of each riser segments, causing some inaccuracy during time domain analysis.

In order to describe the kinematics of the risers experiencing large displacements, the present work utilizes the total Lagrangian formulation in the time-domain dynamic analysis. This method provides an exact strain and stress basis by relating the current and initial configuration. The strain components of the body subjected to configuration changes are described as Eq. (1). The strain components, $E_{ij}$, referred to as Green-Lagrange strain tensor provides a consistent differential operator to obtain the magnitude of deformation in the body. The stress conjugate to this stress is called as Piola-Kirchoff 2^nd stress tensor. Both the strain and stress components are symmetric regardless of the coordinate since the strain measurement is derived from the deformation gradient tensor.

$$ e_{ij} = \frac{1}{2}\left[ {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} + \frac{{\partial u_{k} }}{{\partial x_{i} }}\frac{{\partial u_{k} }}{{\partial x_{j} }}} \right] $$

(1)

$$ s_{ij} = C_{ijkl} e_{kl} $$

(2)

Where:

$i, j, k$:

: base unit in initial configuration

$u$:

: displacement in initial configuration.

$x$:

: spatial coordinate in initial configuration

$C_{ijkl}$:

: constitutive matrix.

In the total Lagrangian formulation, the framework remains consistent since the effects of changes in configuration are already formulated in the formulation of the strain and stress tensor. The real virtual works of the deformed body, as shown in Eq. (3), is energetically equal to that obtained with Green-Lagrange strain and Piola-Kirchoff 2^nd stress, note Eq. (4). The changes in configurations are successfully expressed in the fixed forms by rebuilding the strain and stress. Nevertheless, the integration of internal energy still contains higher order terms, which makes the problem nonlinear to displacement fields. The complete form of virtual work, Eq. (4), thus linearized and re-expressed in iterative form, note Eq. (5).

$$ \int_{V} {\tau_{IJ} \,\delta \varepsilon_{IJ} dV} = R $$

(3)

$$ \int_{{v{}_{{}}^{{t +\Delta }} }} {{}_{{}}^{{t +\Delta {\text{t}}}} s_{ij} \,\delta {}_{{}}^{{t +\Delta {\text{t}}}} e_{ij} } dv = {}_{{}}^{{t +\Delta {\text{t}}}} R $$

(4)

$$ \int_{v} {{}^{{\Delta {\text{t}}}}C_{ijkl} } {}_{0}^{{\Delta {\text{t}}}} \bar{e}_{kl} \delta {}_{{}}^{{\Delta {\text{t}}}} \bar{e}_{ij} dv + \int_{v} {{}_{0}^{t} S_{ij} } \delta {}_{0}^{{\Delta {\text{t}}}} \bar{\eta }_{ij} {\text{dv}} = {}_{{}}^{t + \Delta t} R - \int_{v} {{}_{0}^{t} S_{ij} } \delta {}_{0}^{{\Delta {\text{t}}}} \bar{e}_{ij} dv $$

(5)

Where:

${}^{{\Delta t}}\bar{e}$:

: linear strain increment, $\frac{1}{2}\left( {{}_{{}}^{{\Delta t}} u_{i,j} + {}_{{}}^{{\Delta t}} u_{j,i} + {}_{{}}^{t} u_{k,i} {}_{0}^{{\Delta t}} u_{k,j} + {}_{{}}^{{\Delta t}} u_{k,i} {}_{{}}^{t} u_{k,j} } \right)$

$t$:

: time

$v, V$:

: volume of body in initial, deformed configuration, respectively

$C_{ijkl}$:

: constitutive matrix.

$I, J$:

: base unit in deformed configuration

$R$:

: external force

$\Delta t$:

: time increment

$\varepsilon ,e$:

: Cauchy strain and Green-Lagrange strain

${}^{{\Delta t}}\bar{\eta }$:

: nonlinear strain increment, $\frac{1}{2}\left( {{}_{{}}^{{\Delta t}} u_{k,i} {}_{{}}^{{\Delta t}} u_{k,j} } \right)$

$\tau ,S$:

: Cauchy stress and Piola-Kirchoff^2nd stress

The riser element model is formulated on the base of total Lagrangian as shown in Fig. 1. The element contains two nodes having 6-degree of freedom and the third order Hermite polynomials are utilized to shape functions, Fig. 1(a). The solution algorithm proceeds with the Newton-Raphson algorithm in which the stiffness and internal vectors are iteratively updated until the equilibrium with external force, Fig. 1(b).

Fig. 1.

Kinematics of riser segments in total Lagrangian formulation: (a) 6-degree of freedom element and (b) force equilibrium during iterative solution

The test result for the validation of solver is depicted in Fig. 2. The test structure has a fixed clamp in the left end and subjected to vertical load until the end section reaches vertical Fig. 2(a). The exact solution to this problem is well derived by Chen (2010). He suggested an integral form for the cantilever structure under the large deflection and the presented equation showed good agreement to the experiment results. The numerical analysis results on the deflection of 120 m cantilever beam structure are graphed on and compared with exact solutions, Fig. 2(b). The result shows that the present formulation well predicts the large deflection of slender, even though the midsection vertically folds with severe deflection.

Fig. 2.

Large deflection test result: (a) cantilever beam for test and (b) result of validation against exact solution

2.2 Seabed Interactions

The interaction between riser structures and seabed results the intensive bending stress along the touchdown region, whereby the normal force induced by the penetration of the riser into seabed surface should be reflected into the static and dynamic analysis. In the present work, the riser-seabed interaction model is established under the basis of the node to a contact algorithm.

The contact algorithm reflects the interaction between the riser structures and seabed in an iterative way. During the dynamic analysis, the algorithm measures the clearance distance of all nodes to search for potential contact regions. The clearance distance is defined as the vertical distance between the node and the seabed. When some nodes become below the elevation of the seabed, the algorithm supplements the normal stiffness and additional restoring force induced by the seabed.

Figure 3 illustrates how the contact algorithm reflects the interaction. The normal force on the beam element after the penetration is in proportional to the contact area of the outer surface. Presuming that the cross-section of flexible risers maintains a small ovality, the surface area is in proportional to the penetration depth of the element. The corresponding contact force is derived by the multiplication of the contact surface with normal stiffness of the given seabed. This value determines the additional normal stiffness per unit length, so the beam element subjected to the penetration re-formulate the constitutive matrix.

Fig. 3.

Riser-seabed interaction model: (a) estimation of contact surface and (b) pure penalty method

The normal stiffness of each beam element is determined based upon each node’s penetration status, as indicated in Fig. 3(b). Individual cases categorize the potential penetration status of beam elements during the analysis. The first case represents that two nodes are buoyant state, in which the element maintains the positive seabed clearance. On the contrary, case 2 shows a partially penetrated beam element, where some part of the element is penetrating the seabed but the other part maintains the clearance. In this case, the area of the penetrating part is approximated by the vertical displacement of two nodes and the corresponding bending stiffness is assigned in accordance with the penetration state. The buoyant part of the element is not affected by the seabed, but the normal stiffness is also supplemented to this part since the beam element contains two nodes. The last case indicates the full penetrating state, which indicates that two nodes are below the elevation of the seabed and their downward displacement is controlled by the seabed stiffness. Likewise in case 2, the normal stiffness and the restoring force from seabed highly depend on the contact area and the depth of the penetration. Accordingly, the distribution of contact surface and normal stiffness along the length of the beam element is approximated by the position of two nodes.

The seabed stiffness of the beam elements are assumed to exert the restoring force in the normal direction of the axis, therefore the supplemented matrix is rotated in accordance with the rotated angle. At the same time, the restoring force from the interaction between the seabed and riser structures are directly estimated by multiplying the penetrated displacement with the generated seabed stiffness in each iteration. Therefore, the solution algorithm continuously updates the contact states until it reaches equilibrium states.

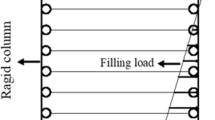
The simple test on contact algorithm is conducted as shown in Fig. 4. The test model is a simple pipeline structure having the length of 120 m and laid out straight towards the axial direction. It is identified that the current contact algorithm shows good agreement to that from the commercial program, Orcaflex.

Fig. 4.

Seabed interaction benchmark test

The accuracy of developed solver accompanying the interaction of riser and sea-bed is validated against the commercial dynamic analysis software, Fig. 5. The test is a vertical upload of 120 m steel riser with 400 ton on the free-hang point. The seabed has 60 kN normal stiffness considering the property of a mud. The results computed by the current solver show good agreement with those by Orcaflex. Although the suggested riser-seabed interaction method, differently from Orcaflex, is based on the pure penalty method, it is concluded that the solver can obtain the distribution of cross-section resultant without inaccuracy.

Fig. 5.

Results of benchmark test against Orcaflex: (a) deformed shape, (b) shear force, (c) tension, and (d) bending moment

2.3 Time Marching Scheme

The dynamic analysis of riser structures normally entails various nonlinear characteristics induced by structural and environmental causes. In example rapid rotation of riser elements generates continuous changes in global stiffness, therefore they undergo dynamically non-Gaussian vibration. These intrinsic nonlinearities of riser structures necessitate the use of direct time marching schemes rather than modal analysis.

Therefore, the current research utilizes the Newmark-β scheme to integrate the time derivatives of displacement fields. The Newmark-β scheme formulates the governing equations by approximating the unknown values from several critical points. The velocity and displacement at the time, $t_{i + 1}$, is approximated from the acceleration, Eq. (6) and (7). The dynamic equation of the system, Eq. (8), is therefore denoted in terms of displacement increments considering the inertia and damping effects, Eq. (9).

$$ x\left( {t_{i + 1} } \right) = x_{i} + \Delta t\dot{x}_{i} + \Delta t^{2} \left[ {\left( {\frac{1}{2} - \beta } \right)\ddot{x}_{i} + \beta \ddot{x}_{i + 1} } \right] $$

(6)

$$ \dot{x}\left( {t_{i + 1} } \right) = x_{i} + \Delta t\left[ {\left( {1 - \gamma } \right)\ddot{x}_{i} + \gamma \ddot{x}_{i + 1} } \right] $$

(7)

$$ M\ddot{x}\left( t \right) + C\dot{x}\left( t \right) + Kx\left( t \right) = f $$

(8)

$$ \left[ {\frac{6}{{\Delta t^{2} }} + \frac{3}{{\Delta t}}C + K} \right]\delta x_{i} = \delta f - \delta R + \left[ {3M + \frac{2}{{\Delta t}}C} \right]\ddot{x}_{i} + \left[ {\frac{6}{{\Delta t}}M + 3C} \right]\dot{x}_{i} $$

(9)

Where:

$f$:

: external force

$x,\dot{x},\ddot{x}$:

: displacement, velocity, acceleration

$C$:

: damping coefficient

$K$:

: stiffness

$M$:

: inertia coefficient

$\upbeta$:

: beta-coefficient

$\upgamma$:

: gamma-coefficient

$\Delta t$:

: time increment

The schematics of the nonlinear dynamic analysis process is described in Fig. 6. From every time increment, the dynamic solver assumes the initial displacement and relevant velocity and acceleration data. The stiffness is updated under the recursive process to meet both the dynamic and contact equilibrium. The process continuously updates every condition of riser status until the residual force bellows a predetermined convergence level.

Fig. 6.

Schematics of nonlinear dynamic analysis process

2.4 Nonlinear Bending Model for Flexible Risers

The contribution of helical wires on the cross section resultant is categorized by the contact status between tensile armor and adjacent anti-friction tape. The helical wires generate bending stress under the relatively low level of curvature. After the overall curvature exceeds the critical level, referred to as critical curvature, some part of wires loses their frictional forces due to the excessive sliding force. The contribution of helical wires to bending moment consequently diminishes and the bending stiffness of the riser section only depends on the other layers.

The theoretical model proposed by Kraincanic and Kebadze (2001) provides an adequate solution to obtain the critical curvature. When helical wires wounding the internal anti-friction tape bent under the critical curvatures the friction forces overcomes the sliding force along the wires, leading the elevation of bending stress. The normal stress of helical wire is derived as Eq. (10). The sliding force along the wires is identical to the differential of axial force towards the helical path, Eq. (11). The slip of helical wires initiates when the sliding force just overcomes the friction force. The friction force on the helical wires in helical direction is in proportional to both side contact force, Eq. (12). Thus, the critical curvature is the equilibrium point of sliding force and friction force, Eq. (13).

$$ \varepsilon_{0} = Rsin^{2} \alpha sin\theta_{j} \beta $$

(10)

$$ \delta N_{0} = Ebtcos^{2} \alpha cos\theta \beta \frac{R}{sin\alpha }\delta \theta $$

(11)

$$ \delta F = \left( {P_{1} k_{1}^{fr} + P_{2} k_{2}^{fr} } \right)b\frac{R}{sin\alpha }\delta \theta $$

(12)

$$ \beta_{cr} = \left( {P_{1} k_{1}^{fr} + P_{2} k_{2}^{fr} } \right)/\left( {{\text{Et}}sin\alpha cos^{2} cos\theta } \right) $$

(13)

Where:

$b$:

: breadth of wire

${\text{t}}$:

: height of wire

$k_{1}^{fr} , k_{2}^{fr}$:

: friction coefficient

$E$:

: modulus of elasticity

$F$:

: friction force

$N_{0}$:

: normal stress on the section of helical wires

$P_{1} , P_{2}$:

: contact pressure on the tensile armor layer

$R$:

: radius of tensile armor layer

$\varepsilon_{0}$:

: normal strain on the section of helical wires

$\beta$:

: curvature

$\beta_{cr}$:

: critical curvture

$\alpha$:

: laying angle

$\theta$:

: angular position of wire.

The contact pressure which restricts the slip of helical wires can be estimated through the static analysis of the riser section under the axisymmetric load. The radial responses for internal and external pressure are obtained based on Eqs. (14)–(17).

The internal strain energy of the polymer sheath is treated as a homogeneous tube, Eq. (14). The overall behavior of internal carcass and pressure armor having highly twist-ed profiles can be approximated by alternating the layer as an orthotropic tube, as shown in Eq. (15). The constitutive matrix for these layers shall be determined in accordance with the FE result of the theoretical approaches. The strain energy of tensile armor layers is calculated through the integration of infinitesimal energy along the cross-section surface, see Eq. (16). The stress of the surface of helical wires is the multiplication of modulus of elasticity and strain expressed in Eq. (10).

$$ U_{iso.} = \frac{1}{2}\int_{v} {\frac{E}{{1 - v^{2} }}} \left( {E\varepsilon_{1}^{2} + 2vE\varepsilon_{1} \varepsilon_{2} + E\varepsilon_{2}^{2} } \right) + G\gamma_{12}^{2} dv $$

(14)

$$ U_{ortho.} = \frac{1}{2}\int_{v} {\left[ {\begin{array}{*{20}c} {C_{11} \varepsilon_{1}^{2} + 2C_{12} \varepsilon_{1} \varepsilon_{2} + 2C_{16} \varepsilon_{1} \gamma_{12} } \\ { + C_{22} \varepsilon_{2}^{2} + 2C_{26} \varepsilon_{2} \gamma_{12} + C_{26} \varepsilon_{2} \gamma_{12} } \\ \end{array} } \right]} dv $$

(15)

$$ U_{wire} = \frac{1}{2}\sum\nolimits_{j = 1}^{m} {\int_{v} {\sigma_{1} \varepsilon_{1} dv} } $$

(16)

Where:

$C$:

: constitutive matrix

$E$:

: modulus of elasticity

$\gamma$:

: normal shear strain

$\varepsilon$:

: normal strain

$\sigma$:

: normal stress.

The nonlinear bending model based on the theoretical approach is validated against FEA. The bending hysteresis curve for 7-in. internal diameter flexible riser subjected to internal and external pressure is shown in Fig. 7. The result computed by the bending model shows good agreement to that from FEA. It is concluded that the nonlinear bending model can be considered into the dynamic analysis in a large-scale approach.

Fig. 7.

Validation results of nonlinear bending model for 7-in. internal diameter flexible riser

The bending nonlinearity of flexible risers is adopted on the dynamic analysis in accordance with the update process shown in Fig. 8. The element stiffness in bending contains stick and slip state value whereby the dynamic solver changes the element property depending on the nodal curvature. The element maintains the high resistance in bending when the nod-al curvature stays below the critical curvature. Otherwise, the helical wires are treated as the slip state, and the iterative update process reassigns the internal force with a reduced bending moment.

Fig. 8.

Update process of nonlinear bending during dynamic analysis

3 Dynamic Analysis Test

In this study, the dynamic analysis considering the nonlinear bending stiffness of flexible risers is demonstrated. Furthermore, the effect of nonlinearity in the large-scale analysis is investigated by comparing the results from the nonlinear model with those from the linearized beam model. The nonlinear bending property originates the pressure distribution in the seabed, thus the riser element changes its bending stiffness after the critical curvature. The test is conducted for the internal diameter of 7-in. flexible riser. The details of the test riser are described in Fig. 9.

Fig. 9.

Details of internal diameter of 7-in. flexible riser

3.1 Pure Vibration Test

Pure vibration test on the relatively small size of the flexible riser is conducted as Fig. 10. The right end side of the riser is clamped, which causes progressive bending moment growth along the length. The left side, end tip, is subjected to the dynamic vertical force with 1.0 kN and 10 s period, Fig. 10(a). The linear bending model assumes that no friction between the helical wires and the other layers. Consequently, the bending stiffness of this model is consistent regardless of exposed curvature, and only the geometric nonlinearity is involved during the dynamic analysis. Meanwhile, the non-linear bending model maintains relatively high bending stiffness unless the riser element exceeds the critical curvature. After the curvature grows more than the critical curvature, the bending stiffness dramatically reduces.

Fig. 10.

Schematics of pure vibration test: (a) Test model and bending property of comparing two models, (b) dynamic response at the end tip

The time history of the vertical displacement at the end tip shows the effect of bending nonlinearity of the flexible riser, see Fig. 10(b). The dynamic responses of linear bending model smoothly increase with the low bending stiffness. In case of the nonlinear bending model, unlike to those of linear bending model, the displacement of the end tip remains relatively lower than in the bending model since its bending property. The dynamic responses suddenly increase after the critical curvature, due to the exceedance of curvature level.

3.2 Free-Hang Vibration Test

Free-hang vibration test is demonstrated to test the dynamic behavior of flexible riser interacting the seabed. Linear and nonlinear bending model also used in this test for the investigation. The models have 120 m length and dynamically loaded by using the dynamic boundary condition at the fairlead.

The initial configuration of the risers are obtained through the static analysis in order to reflect the actual installation procedure, Fig. 11. The riser structure is first laid down on the seabed surface which set to be 300 m from the mean water line. The deformed state of the riser with its weight is calculated, therein most force from the riser weight is supported by the seabed. After the weight is loaded the vertical uploading of fairlead point is conducted. Using the Lagrange multiplier, the position of the fairlead point is adjusted to the predetermined value. Fairlead point is finally adjusted to meet the user-determined value. The dynamic analysis initiates when the initial configuration of the riser is obtained.

Fig. 11.

Load sequence in analysis test

The static responses of nonlinear bending model and the linear bending model are compared in Fig. 12. The configuration after the vertical uploading of fairlead and horizontal adjusting is represented in Fig. 12(a) and (b), respectively. The linear model, different from the nonlinear bending model, shows much different deformed shape across the touchdown zone. This implies that even though both models have an identical property in bending after the critical curvature, the nonlinear bending model results in some difference from linear bending model.

Fig. 12.

Comparative study results: (a) static analysis results after vertical uploading and (b) static analysis result after horizontal adjusting

Some discrepancies between two models are also identified in bending hysteresis curve, Fig. 13. The curvature of the comparing models increases during the vertical uploading and decreases while the horizontal adjusting stage. The cross-section bending moment in the nonlinear bending model grows much higher than the linear bending model due to the contribution of the friction stress in helical wires. The slope in bending moment reduces after the critical curvature since the friction between the helical wires and other layers is neglected based on the slip initiation.

Fig. 13.

Bending hysteresis curve of riser segment near touch down zone

Time domain history of critical points is shown in Fig. 14. The deformed shape after the horizontal adjustment in the nonlinear bending model shows different results than in the linear bending model. The results show that the nonlinear bending model maintains stable vibration during the dynamic analysis. Meanwhile, during the vibration, the amplitude of displacement in the nonlinear bending model is almost similar to that of linear bending model. Different from those in the pure vibration test, the range of dynamic responses of two models rather similar to each other. Observing the vertical displacement of the sample point near the touchdown zone, the nonlinear bending model results in approximately 0.033 m of vertical vibration. The linear bending model shows about 0.038 m of vertical vibration near the touchdown zone, which seems similar to the results of the nonlinear bending model.

Fig. 14.

Vertical displacement time domain history: (a) displacement near touch down zone and (b) displacement near fairlead

It is concluded that the riser vibrating under relatively small amplitude loading results in similar dynamic responses because the curvature responses remain small, and the curvature level of most element exceeds the critical curvature level.

4 Conclusion

The current study has dealt with the development of the global dynamic analysis for flexible risers. Based on the theoretical approaches, the dynamic analysis solver for flexible risers, OPFLEX is developed and demonstrated for the validity. The beam elements of riser models are generated by the total Lagrangian formulation to describe the variation of configuration due to large deflections. To model the detailed effects of the interaction between risers and seabed, the contact algorithm is developed and involved in the analysis procedure. During the analysis, the contact algorithm updates the contact status of every beam element and restoring force induced by the penetration, so the movements of risers are fully coupled with the seabed. The nonlinear behavior of flexible risers is modeled by updating the property of beam elements in accordance with the critical curvature. When the curvature of beam elements exceeds their threshold, the bending stiffness rapidly decreases considering that all helical wires undergo slippage. For the validity of the developed analysis solver, several case studies are carried out and the results are discussed. Through the case studies, it is identified that the nonlinear bending behavior of flexible risers reduces the curvature responses until they overcome the critical curvature but maintains similar responses to that of the linearized model after the slippage. The suggested method is still under development. The nonlinear bending model of beam element should be improved to describe progressively decreasing bending stiffness and be coupled with rapidly changing axial force.