Scantling Evaluations of Plates and Stiffeners Based on Elasto-Plastic Analysis Under Axial Loads and Lateral Pressures

Abstract

This paper presents a method for deriving the practical collapse strength against lateral pressure of hull local members such as plates and stiffeners which makes use of non-linear FEA calculations. Unlike the collapse strength against compressive axial loads, the collapse strength against lateral pressure cannot be clearly identified because such structures are capable of withstanding lateral pressure caused by membrane stress even though they may deform plastically. This paper, therefore, defines “collapse” to be the condition in which residual deflection develops up to a defined criterion after the unloading of both axial loads and lateral pressures, where the maximum lateral pressure that does not cause “collapse” is regarded to be the practical collapse strength. Utilizing this criterion, the practical collapse strength against lateral pressure of various types and scantlings of plates and stiffeners is investigated and compared with the assessment formulae for hull local members specified in the International Association of Classification Societies’ (IACS) Common Structural Rules (CSR). Additionally, the effects of the axial loads acting together with lateral pressures are also studied. The results of the study show that compressive axial loads are more critical than tensile axial loads with respect to collapse strength. For thinner plates and smaller stiffeners, tensile axial load gains their collapse strength. The out-plane component of internal force due to the axial load is considered to cause these phenomena.

1 Introduction

1.1 Background

Hull local members such as plates and stiffeners are the most fundamental components of a ship’s hull structure. The arrangements and scantlings of these members are basically determined so as to ensure that they are capable of withstanding lateral pressures such as water pressure or cargo pressure. In addition, hull girder bending moment acts upon these local members as axial load. Thus, the combination of axial load and lateral pressure simultaneously acting upon them needs to be considered.

In order to ensure sufficient structural safety for ships, the structural rules specified by classification societies typically require two types of strength evaluations be carried out for hull local members, and these are as follows:

• strength evaluation against axial compression load, and

• strength evaluation against lateral pressure in consideration of strength reductions due to axial loads.

The former is based upon elastic/plastic buckling theory for both plates and stiffeners and is related to the prevention of local buckling, whereas the latter is based upon elastic beam theory for stiffeners and rigid-plastic analysis for plates and is related to determining whether there is sufficient strength against lateral pressure.

In recent years, the use of non-linear FEA which can take into account large displacement and elasto-plasticity has become increasingly popular. The knowledge obtained from non-linear FEA results has not only revealed the collapse behavior of plates and stiffeners subjected to a combination of high axial compression loads and low-level lateral pressures (hereinafter referred to as the “axial load dominant condition”), but has also made possible the development of a number of closed-form simplified formulae which can be used to estimate the collapse strength of plates and stiffeners. Classification societies have incorporated these simplified closed-form formulae into their class structural rules as a way of improving the rationality of their strength evaluations, which in turn leads to greater ship safety.

With regard to the strength assessments for loading conditions in which a combination of high-level lateral pressures and low-level axial loads is acting (hereinafter referred to as the “lateral pressure dominant condition”), the class structural rules of most classification societies still use conventional formulae based upon elastic beam theory and rigid-plastic analysis. Taking into account the long track record of their successful application to huge number of ships, these conventional formulae are deemed to ensure sufficient safety for hull local member design.

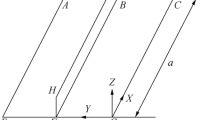
For many years now, rigid-plastic analysis has been the standard way of assessing the collapse strength of plates or stiffeners against lateral pressures, and conventional rigid-plastic analysis considers the collapse mechanism shown in Fig. 1 (a). When a section in a beam entirely reaches its yield stress $\sigma_{Y}$ due to bending stress (Fig. 1 (b)), this point becomes “plastic hinge” that cannot withstand larger bending moments. When a collapse mechanism such as that shown in Fig. 1 (a) develops, rigid-plastic analysis regards the structure to be “collapsed”. When the axial load for the beam is applied, the area around plastic neutral axis is occupied by axial load. The neutral axis in a section, therefore, changes (Fig. 1 (c)) and the maximum capable bending moment (fully plastic moment) decreases.

Fig. 1.

Conventional rigid-plastic analysis concept

Past studies into the collapse strength and plastic deformation behavior of stiffened or unstiffened plates against lateral loads have been carried out by many researchers. Jones [1] proposed a theoretical rigid-plastic analysis for beams and plates considering the effect of small axial displacement at the boundary, while Manolakos [2] presented a method to estimate collapse strength of grid structures using the end-fixity coefficient and Schubak [3, 4] developed a rigid-plastic model of stiffened plates subjected to uniformly distributed blast loads. For blast loads, Louca [5] predicted the dynamic response of unstiffened plate using Lagrange’s equation and carried out non-linear FEA, whereas Hong [6] utilized plastic yield line theory to propose a “Double-diamond” collapse model of plates for a laterally patch load. With regard to experimental study, Shanmugam [7] performed experiments for stiffened plates subjected to axial compression and lateral pressure, and then compared the results with those obtained using with non-linear FEA, while Yu [8] proposed a method to estimate resistance-deformation curve of stiffened plates subjected to lateral loads which is capable of taking into account stiffness for the inward motion of stiffener ends.

Past studies on the collapse strength in lateral pressure dominant condition, however, did not consider the idea of “residual deflection” after unloading. There is, therefore, a possibility that significant residual deflection will occur in a hull local members even though the local member does not reach its collapse strength. The authors consider that any residual deflection which causes strength degradation should be avoided so as to preserve ship hull structural safety.

Additionally, in most past studies, the difference between tensile and compressive axial loads acting together with lateral pressure is not discussed sufficiently. In this paper, to improve the assessment method based on conventional rigid-plastic analysis theory and to make it possible to give hull local members more rational scantling, the collapse strength from the perspective of residual deflection of various types and scantlings of plates and stiffeners in the lateral pressure dominant condition is derived by using non-linear FEA. And the effects of axial loads for the collapse strength are studied. In addition, the strength criteria specified in CSR [9] are studied in comparison to derived values of collapse strength.

1.2 Deriving Collapse Strength Against Lateral Pressure Using Non-linear FEA

When hull local members are in the axial load dominant condition, an abrupt drop in the load-displacement curve (Fig. 2(a)) is observed after the yielding or buckling, and the maximum axial load value can be defined as collapse strength against axial load; however, when such members are in the lateral pressure dominant condition, deflection by the lateral pressure continues to increase (Fig. 2(b)) without any abrupt drop, even though they start to deform plastically, and the moment of collapse cannot be clearly identified by observing deflection-lateral pressure curve in cases where the curve is derived from non-linear FEA without considering fractures of material. This behavior is known to be caused by the membrane stress effect.

Fig. 2.

Typical collapse behavior of hull local members

This paper defines “collapse” to be the condition in which residual deflection develops up to a defined criterion after the unloading of both axials load and lateral pressures. This assumption is based upon actual cases where excessive permanent deformation is considered to decrease strength against future severe loading conditions and is regarded as the damage to be repaired. Using this criterion, the highest lateral pressure which does not induce collapse can be examined from a series calculation of non-linear FEA in which the maximum values of lateral pressure are changed. The criterion for residual deflection after unloading is determined by the initial deflection considered in typical buckling analysis such as plate breadth/200 or 0.1% of longitudinal span. These values are similar to “Ship building quality standard for new construction” such as IACS Rec 47 [10] and generally recognized as the sufficiently small deformations that do not affect for the strength of hull local members.

2 Non-linear FEA Model and Analysis Conditions

This paper derives practical collapse strength based upon the residual deflection criterion described in Sect. 1.2 using the commercial FEA software LS-DYNA. Section 2.1 describes the conditions and procedures for deriving the collapse strength of plates, while Sect. 2.2 does the same for the collapse strength of stiffeners. The study uses LS-DYNA implicit method, and convergence studies are performed before the analysis so as to derive the collapse strength of hull local members. This is done to determine proper model mesh size and load increment interval of the non-linear FEA, these convergence studies compare past experiments carried out by Fujii [11] and Tanaka [12], which respectively observed the collapse behavior of plates and stiffened plates. Fujii [11] carried out experiments in which plates are subjected to lateral pressure until the plates fracture, and then observed the development of deflection and the residual deflection after unloading for several lateral pressures. Figure 3 shows one of the comparisons of deflection during loading and residual deflection after unloading between the experiment carried out by Fujii [11] and the non-linear FEA that produced the experiment. It can be seen that FEA results are in good agreement with the experimental results. Therefore, the mesh size and load incremental intervals of non-linear FEA that give good agreement with experimental results are adopted.

Fig. 3.

Comparisons of experimental results from prior studies to non-linear FEA results

2.1 Plates

FEA Model.

As shown in Fig. 4, four plates which are separated by stiffeners and transverse girders are modelled by shell elements. Only plates are modelled, with stiffeners and girders being expressed by constraining the deflection of the plates. The specifications and material parameters of the plates are shown in Table 1 and Table 2, respectively.

Fig. 4.

Analysis model and FEA boundary conditions for plates

Table 1. Plate specifications

Table 2. Material parameters for non-linear FEM analysis

Boundary Conditions.

This paper uses the periodic boundary condition proposed by Fujikubo [13] for the model edges. This boundary condition can realize that the modeled plate infinitely continues in both longitudinal and transverse directions. This assumption is consistent with a practical ship hull structure that is composed by large number of continuous stiffened plates. By using this boundary condition for four plates shown in Fig. 4, both any plate buckling mode and lateral deformation due to lateral pressure can be considered. The details of the boundary conditions used in the plate analysis are shown in Table 3.

Table 3. FEA boundary conditions for plates

Analysis Method and Load Conditions.

To investigate residual deflections after unloading and deriving collapse strength, the three-step analysis shown in Table 4 is carried out. Axial loads are applied to the model edges in Step 1; then, as shown in Fig. 4, the transverse axial load case (axial load for the long edge of the plate) and longitudinal axial load case (axial load for the short edge of the plate) are considered. Both compressive and tensile axial loads are also considered for both direction loads, and the magnitudes of the axial loads are shown in Table 5. Since the axial loads for hull local members are generated by the hull girder longitudinal bending moment, the cases where transverse axial load is applied assume a transverse framing structure; others cases, on the other hand, assume a longitudinal framing structure.

Table 4. Three-step analysis for deriving collapse strength

Table 5. Axial load values for plates

Definition of Collapse Strength.

The “collapse” of plates in non-linear FEA, which is described in Sect. 1.2, is defined as the condition in which residual deflection after the unloading of both axial and lateral pressures is developed up to “plate breadth/200 [mm]” (in this paper, 800 mm/200 = 4.0 mm). The maximum lateral pressure that does not induce “collapse” is derived for each plate thickness and load case through iterative changes to maximum lateral pressure, and a flow chart of the process for deriving collapse strength is shown in Fig. 5. For plate analysis, the magnitude of deflection is measured at the center of the plate.

Fig. 5.

Collapse strength derivation process flow chart

An example of the procedure for deriving collapse strength is shown in Fig. 6. This figure shows the deflection history of 20 mm plate thickness for some cases with different maximum lateral pressure. In Step 3 of Fig. 6, unloading the lateral pressures and axial loads, the deflection decreases and the residual deflection can be observed at the last point of Step 3. In this case, a value 1.155[MPa] is used for the maximum lateral pressure so that the residual deflection does not to develop up to 4 mm. Thus, the collapse strength of a 20 mm plate can be determined to be 1.155 MPa. This method was applied to each load case and each plate thickness and the collapse strength and the effects of axial loads on collapse strength are investigated.

Fig. 6.

Example of history of deflection to derived the collapse strength

2.2 Stiffeners

FEA Model.

A stiffened plate with a T-type stiffener is modelled by shell elements. 2-longitudinal space (1/2 + 1+1/2) - 1-transverse space (1/2 + 1/2) model is used as shown in Fig. 7. The longitudinal span of the model is 4,000 mm, and the spacing between stiffeners is 800 mm. The dimensions of stiffeners considered in this paper are shown in Table 6, and the plate thickness is assumed to be 20 mm for all models. In the model, longitudinal span is divided into 80 elements and transverse space is divided into 16 elements, with the stiffener web being modelled by shell elements of 50 mm in height; for example, a stiffener web of 150 mm in height is to be divided into three elements in the height direction. The face plate is divided into two elements in the width direction, and the material parameters are same as those used for plate analysis shown in Table 2.

Fig. 7.

Analysis model for FEA of stiffeners

Table 6. Dimensions of stiffeners

Boundary Conditions.

The boundary conditions for the stiffeners are shown in Table 7. The symmetry condition is used for all model edges, with the x-directional displacement between the nodes being fixed for edge AD (the edge subjected to the axial load. shown in Fig. 7) so that it remains straight during analysis, and the y-directional displacement between the nodes being fixed for edge AB. At the lines of the transverse members in Fig. 7, the z-directional displacement is fixed, and y-directional displacement between nodes of the web is fixed to prevent any tripping of the stiffener.

Table 7. FEA boundary conditions for stiffeners

Analysis Method and Load Conditions.

The same three-step analysis used for plate analysis described in Table 4 is also adopted for stiffener analysis. As shown in Table 8, the axial loads for stiffeners are applied so that the average stress is between 10% and 70% of yield stress $\sigma_{Y}$ at 10% increments, and both tensile and compressive loads are considered respectively. Additionally, lateral pressures from the plate side and stiffener side are also considered.

Table 8. Axial load values for stiffeners

Definition of Collapse Strength.

The “collapse” strength of stiffener is derived the same way as is done during plate analysis as shown in Fig. 5. The criterion of residual deflection after unloading for stiffeners is defined as “0.1% of transvers space” (in this paper, 0.1% of 4000 mm = 4 mm). In the same manner is done for plate analysis, maximum lateral pressures that do not induce collapse are derived for each load condition and dimension shown in Table 6. For stiffener analysis, the magnitude of deflection is measured at point E in Fig. 7, with the point being at the mid span of stiffener and the cross point of the stiffener and attached plate.

3 Collapse Strength of Plates Derived by Non-linear FEA

3.1 Collapse Strength of Plates

As an example of the results of plate analysis, a von Mises stress contour plot of 20 mm plate thickness in the pure lateral pressure case is shown in Fig. 8. In Fig. 8 (a), when maximum lateral pressure 1.155 MPa is applied (at the end of step 2 described in Fig. 5), the stresses at the center and transverse edge of plates where large bending moment acts reach yield stress. In Fig. 8 (b) residual stress and residual deflection is observable when lateral pressure is completely unloaded (at the end of Step 3).

Fig. 8.

Von Mises stress contour of 20 mm plate thickness in pure lateral pressure case

A comparison of collapse strength values of plates derived by the procedure described in Fig. 5 and some analytical methods in pure lateral pressure case is shown in Fig. 9. As the analytical methods, we employed 3-point plastic hinge theory and roof shaped collapse theory. A unit width of plates was considered in the application of 3-point hinge theory (i.e., aspect ratio was assumed infinite). It can be observed that the collapse strength derived by FEA is similar to the roof shaped collapse theory.

Fig. 9.

Comparison of collapse strength of plates in pure lateral pressure case

The collapse strength values of plates derived by the procedure described in Fig. 5 considering axial load are shown in Figs. 10–13. In addition, the criteria required by the assessment formulae of CSR [9] are also plotted in these graphs. The details of the CSR formulae are described in the appendix.

Fig. 10.

Collapse strength of plates of compressive-transverse axial load case (transverse framing structure)

Fig. 11.

Collapse strength of plates of tensile-transverse axial load case (transverse framing structure)

Fig. 12.

Collapse strength of plates of compressive-longitudinal axial load case (longitudinal framing structure)

Fig. 13.

Collapse strength of plates of tensile-longitudinal axial load case (longitudinal framing structure)

A comparison to the collapse strength derived by FEA in transverse axial load cases (Fig. 10 and Fig. 11) shows that large decreases in collapse strength due to compressive axial loads are observable, while the effects of tensile axial loads upon collapse strength are smaller than those of compressive axial loads. Moreover, the effect of axial load is observed to be smaller than that of transverse axial load (Fig. 10 and Fig. 11) with respect to the longitudinal axial load case (Fig. 12 and Fig. 13).

A comparison of the pure lateral pressure case for FEA with that for the CSR formulae in Figs. 10–13 (i.e. the same values are plotted in these graph with regard to pure lateral pressure case) shows the values of collapse strength derived by non-linear FEA are at least 40% higher than the CSR criteria for each plate thickness. In addition, the collapse strength derived by non-linear FEA in all cases with axial loads acting is higher than the CSR criteria, with the ratio between the two varying according to the axial load condition. These comparison results prove that the CSR formulae do avoid residual deflection for each plate thickness and each load conditions with a sufficient margin of safety.

It is noted that cases where collapse caused by only axial compression (i.e. buckling collapse) occurs are not plotted in these graphs; for example, the plot of “Axial load 200 [MPa]” in Fig. 10 starts from a plate thickness of 26 mm, with the collapse strength at plate thicknesses 6 mm to 24 mm not being considered. This is because buckling collapse occurs within this range of plate thicknesses at the beginning of Step 2.

3.2 Discussions on the Reduction of Collapse Strength for Plates

In order to discuss the effects of axial loads on collapse strength, collapse strength reduction for the pure lateral pressure case is investigated. Figures 14–17 show the reduction ratio of collapse strength for some representative plate thickness cases, including that of the CSR.

Fig. 14.

Reduction of collapse strength of plates of compressive-transverse axial load case (transverse framing structure)

Fig. 15.

Reduction of collapse strength of tensile-transverse axial load case (transverse framing structure)

Fig. 16.

Reduction of collapse strength of plates of compressive-longitudinal axial load case (longitudinal framing structure)

Fig. 17.

Reduction of collapse strength of plates of tensile-longitudinal axial load case (longitudinal framing structure)

In the compressive axial load cases shown in Fig. 14 and Fig. 16, collapse strength is reduced at a regular rate in proportion to the magnitude of the compressive axial load and the reduction in the transverse axial load case is more significant than that in longitudinal axial load case.

In the tensile axial load cases shown in Fig. 15 and Fig. 17, on the other hand, the tendency of reduction depends upon not only the direction of axial load, but also plate thickness. For thinner plates such as 6 mm and 10 mm, opposite effect with respect to collapse strength is observed (i.e. the tensile axial load leads to increases in collapse strength depending upon load magnitude). Even though tensile axial loads slightly reduce the collapse strength of thicker plates, the reduction effect is quite smaller than that in compressive axial load cases. It can be also observed that the effects of axial loads in the transverse axial load case are larger than those in the longitudinal axial load case.

Neither conventional theory nor past studies (as previously discussed in Sect. 1.1) have been able to sufficiently reproduce the above-mentioned phenomena, especially those cases where the tensile axial loads leads to increases in the collapse strength of plates. The authors assume that the “axial load effect on the deflection” is one of the factors of above phenomena. Figure 18 shows that a difference in the direction between the internal forces acting upon both sides is developed by transitioning the deflection angle into the small element “dx” of a plate which has deflection w with the axial load σ_xt_p being applied. This means that the distributed load q expressed by Eq. (1) occurs as the out-plane component of the internal force of the plate.

Fig. 18.

Plate which has deflection with axial load acting

$$ q = \sigma_{x} t_{p} \frac{{\partial^{2} w}}{{\partial x^{2} }} $$

(1)

In the compressive axial load cases shown in Fig. 18 (a), the distributed load q is superimposed upon the lateral pressure, which in turn increases its deflection. In the tensile axial load cases, on the other hand, the distributed load q cancels the lateral pressure as shown in Fig. 18 (b), which in turn decreases its deflection. Since the distributed load q is related to the curvature of the plate (second derivatives of deflection w), the effect of axial load on collapse strength becomes large when the deflection angle changes sharply.

To study the magnitude of the effects of distributed load q for each plate thickness, the deflection of plates in pure lateral pressure cases where the maximum lateral pressure is applied at the end of Step 2 is shown in Fig. 19. It is, of course, observed that the deflection becomes large for thinner plates, such as those who thickness is 6 mm; this means that curvature, therefore, becomes larger as a result, and the distributed load q greatly impacts the collapse strength for these thinner plates. This mechanism can explain the reason why the tensile axial loads increases the collapse strength of the thin plates shown in Fig. 15 and Fig. 17. When plate thickness increases, the effect of the distributed load q gets smaller due to the slight deflection that develops as a result of its large flexural stiffness. It can, therefore, be assumed that the collapse strength of thicker plates is reduced by axial loads in accordance with the conventional theory that the axial load reduces the fully plastic moment of plates as described in Sect. 1.1.

Fig. 19.

Deflection of plates of pure lateral pressure case when maximum lateral pressure is applied

Focusing on the difference between the longitudinal and transverse axial load cases, the deflection angle and curvature in the longitudinal direction of a plate caused by lateral pressure must be smaller than their corresponding equivalents in the transverse direction as shown in Fig. 20. It follows, therefore, that the effect of the distributed load q in longitudinal axial load cases should be relatively smaller than that in transverse axial load cases.

Fig. 20.

Difference of deflection angle between transverse and longitudinal directions

With regard to the CSR formulae, the reduction ratio for the CSR formula is similar to that of compressive-transverse axial load case (Fig. 14) where axial loads most significantly reduce collapse strength. It shows that the CSR formula considers the worst case scenario for the effects of axial loads for safety’s sake.

4 Collapse Strength of Stiffeners Derived by Non-linear FEA

4.1 Collapse Strength of Stiffeners

The collapse strengths for stiffeners derived by the procedure described in Fig. 5 are shown in Figs. 21–24. Additionally, the criteria required by the assessment formulae of CSR [9] are also plotted as is done for plates. It is noted that the stiffener criteria required by CSR are based upon the initial yield strength of the stiffeners. Details of the CSR formulae are described in Appendix.

Fig. 21.

Collapse strength (FEA) and initial yield strength (CSR) of stiffeners (tensile load-plate side pressure)

Fig. 22.

Collapse strength (FEA) and initial yield strength (CSR) of stiffeners (compressive load-plate side pressure)

Fig. 23.

Collapse strength (FEA) and initial yield strength (CSR) of stiffeners (tensile load-stiffener side pressure)

Fig. 24.

Collapse strength (FEA) and initial yield strength (CSR) of stiffeners (compressive load-stiffener side pressure)

With regard to the collapse strength derived by FEA, it decreases in proportion to the magnitude of the axial load in “compressive load-plate side pressure case” (Fig. 22) and the “tensile load-stiffener side pressure case” (Fig. 23), but only decreases in “compressive load-stiffener side pressure case” (Fig. 24) when a large axial load (axial stress = 70% of yield stress) is applied. In the “tensile load-plate side pressure case” (Fig. 21), on the other hand, the effect of the axial load is relatively smaller than other cases.

A comparison of the collapse strength derived by non-linear FEA and the CSR formulae in the pure lateral pressure case (Figs. 21–24) reveals that the collapse strength derived by non-linear FEA is anywhere from 25% to 80% higher than the CSR criteria for each section modulus. In addition, the FEA results are higher than the CSR criteria in all cases where axial loads are applied, except for only the “compressive load-stiffener side pressure case” (Fig. 24). When an axial load of 70% yield stress is applied in this case, the CSR formulae overestimates its strength compared to the collapse strength derived by FEA for some stiffener models; CSR, however, may cover this load condition through buckling assessment.

4.2 Discussions for the Reduction of Collapse Strength for Stiffeners

Figures 25–28 show the reduction in collapse strength for some stiffener models described in Table 6.

Fig. 25.

Reduction of stiffener strength (tensile load-plate side pressure)

Fig. 26.

Reduction of stiffener strength (compressive load-plate side pressure)

Fig. 27.

Reduction of stiffener strength (tensile load-stiffener side pressure)

Fig. 28.

Reduction of stiffener strength (compressive load-stiffener side pressure)

The CSR formulae consider the superimposing or cancelling of bending stress and axial load at the stiffener face of its span end, where the largest bending stress occurs in typical uniform stiffeners. For example, in compressive axial load-plate side pressure case shown in Fig. 29, compressive bending stress at the stiffener face of the span end is superimposed on the compressive axial load. Therefore, in the “compressive load-plate side pressure case” (Fig. 26) and the “tensile load-stiffener side pressure case” (Fig. 27), the CSR formulae take into account the axial load as it reduces the initial yield strength of stiffeners. On the other hand, when the bending stress at the point is canceled by the axial load, the CSR formulae do not take into account the effect of the axial load at all in the “tensile load-plate side pressure case” (Fig. 25) and the “compressive load- stiffener side pressure case” (Fig. 28).

Fig. 29.

Bending stress direction of stiffened plate to which plate side lateral pressure with compressive axial load is applied

With regard to the collapse strength derived by FEA, even though the tensile axial load increases the collapse strength of Model 1 remarkably in the “tensile load-plate side pressure case” (Fig. 25), the collapse strength of other the models is not affected by axial load; however, in both the “compressive load-plate side pressure case” (Fig. 26) and the “tensile load-stiffener side pressure case” (Fig. 27), collapse strength decreases in proportion to the magnitude of axial load, while it is also observed that the reduction of collapse strength in Fig. 26 is larger than that in Fig. 27. Finally, the collapse strength of Model 1 decreases remarkably by compressive axial load in the “compressive load-stiffener side pressure case” (Fig. 28), but the collapse strength of other cases decrease when axial load exceeds about 30% of the yield stress.

The authors assume that axial load effect on the deflection considered in Sect. 3.2 is one of the factors of these phenomena just as is assumed with respect to plates. The common point of the conditions in Fig. 26 and Fig. 27 is the superimposition of bending stress and axial load at the stiffener face of span end as shown in Fig. 29. Since the distributed load q developed by compressive axial load is superimposed on lateral pressure, it can be assumed that the reduction of collapse strength shown in Fig. 26 becomes larger than that shown in Fig. 27 due to the distributed load q; moreover, it is also assumed that the increase in collapse strength of Model 1 in Fig. 25 and the remarkable decrease in strength of Model 1 in Fig. 28 are also caused by the distributed load q. This is because the flexural stiffness of Model 1 is small and thus the effect of the distributed load q is large.

With regard to stiffeners, additional investigation should be carried out to consider their respective collapse mechanisms.

5 Conclusions

The conclusions of this paper are summarized as follows.

• 1. A method for assessing the practical collapse strength of hull local members that are subjected to combination of high-level lateral pressures and low-level axial loads through the use of a residual deflection criterion is developed. The criterion is based upon actual cases where excessive permanent deformation is considered to cause a decrease in strength against future severe loading conditions and is regarded as damage requiring repair. Using this method, the collapse strength of rectangular plates and stiffeners in various load conditions are derived using the non-linear FEA software LS-DYNA.

• 2. With regard to plates, the results and discussions are summarized as follows:

  • Collapse strength values derived by residual deflection criterion are similar to the values derived by roof shaped collapse theory in the pure lateral pressure case.

  • Collapse strength derived by the residual deflection criterion is larger than the criteria required by the CSR formulae both in the pure lateral pressure case and in the combined lateral pressure and axial load cases.

  • With regard to the collapse strength derived by the residual deflection criterion, it is observed that the effect of an axial load on collapse strength is relatively small when the axial load is acting along the longer edge of plate. On the other hand, in cases where an axial load is acting along the shorter edge of plate, a significant axial load effect is observed. It is also observed that a compressive axial load is generally more critical than a tensile axial load with respect to collapse strength, but that, tensile axial load increases the collapse strength of thinner plates.

  • It can be assumed that the reason for the above-mentioned phenomena is related to the fact that a fully plastic moment is reduced by axial load in accordance with conventional theory and as a result an “axial load effect on deflection” exists. This effect is caused by the distributed load q, which is the out-plane component of internal force of the plates that is subjected to axial load and lateral pressure. When a compressive axial load is applied, the distributed load q is superimposed onto lateral pressure which in turn increases the deflection. On the other hand, when a tensile axial load is applied, the distributed load q cancels lateral pressure and, therefore, decreases the deflection. Since the distributed load q greatly affects collapse strength when the curvature of the plate is large, plates with small flexural stiffness are greatly affected by the distributed load q. Additionally, the effects of distributed load q become smaller when an axial load is acting along the longer edge of plate because the deflection angle and curvature caused by the lateral pressure must be smaller than those along the shorter edge of plate.

• 3. With regard to stiffeners, the results and discussions are summarized as follows:

  • When an axial load is superimposed onto the bending stress acting on the stiffener face of span end, the collapse strength derived by the residual deflection criterion decreases in proportion to the magnitude of the axial load. In such cases, the compressive axial load is more critical than the tensile axial load; in other cases, collapse strength of stiffener which has small flexural stiffness is increased by the tensile axial load and decreased by the compressive axial load.

  • The reason for these phenomena can be considered that the distributed load q affects the collapse strength of stiffeners in the same manner as it affects the collapse strength of plates. Further investigation should be carried out to consider the collapse mechanisms of stiffeners.

Appendix

In 2014, IACS published its “Common Structural Rules for Bulk Carriers and Oil Tankers (CSR)” [9] for bulk carriers 90 m or longer in length and for oil tankers 150 m or longer in length. In Sect. 4 of Chapter 6 in Part 1 of CSR, the common requirement formulae for any plating are specified. The formula of requirement thickness for plates is as follows.

$$ 0.0158\alpha_{p} b\sqrt {\frac{P}{{\chi C_{a} R_{eH} }}} \,\left[ {\text{mm}} \right] $$

(2)

where

b: Breadth of plate panel [mm]

P: Design pressure [kN/m²]

χ: Coefficient of flooding condition. (In this paper, to be taken as 1.0)

R_eH: Specified minimum yield stress [N/mm²]

α_p: Correction factor for panel aspect ratio to be taken as follow but not to be taken greater than 1.0

$$ \alpha_{p} = 1.2 - \frac{b}{2.1a} $$

a: Length of plate panel [mm]

C_a: Permissible bending stress coefficient for plate taken equal to:

$$ C_{a} = \beta - \alpha \frac{{\sigma_{hg} }}{{R_{eH} }},{\text{ not}}\,{\text{to}}\,{\text{be}}\,{\text{taken}}\,{\text{greater}}\,{\text{than}}\,C_{a - \hbox{max} } $$

β: Coefficient as defined in Table 9

Table 9. Definition of CSR coefficients for plates

Table 10. Definition of C_s

Table 11. CSR coefficients for stiffeners

α: Coefficient as defined in Table 9

C_a-max: Maximum permissible bending stress coefficient as defined in Table 9

σ_hg: Axial stress [N/mm²]

In Sect. 5 of Chapter 6 in Part 1 of CSR, the common requirement formulae for any stiffeners are specified. The formula of requirement section modulus is as follows.

$$ \frac{{Psl_{bdg}^{2} }}{{f_{bdg} \chi C_{s} R_{eH} }}\,\left[ {{\text{cm}}^{ 3} } \right] $$

(3)

where

s::

Spacing of frames [mm]

l_bdg::

Effective bending span [m]

f_bdg::

Bending moment factor taken as follows:

12 for horizontal stiffeners and upper ends of vertical stiffeners

10 for lower ends of vertical stiffeners

C_s::

Permissible bending stress coefficient as defined in Table 10