Design and Development of Modular Parallel XY Manipulator

Abstract

Flexure mechanism provides precise and repeated motion over a small range. Many monolithic designs have been discussed in the literature however they are costly to manufacture and give no flexibility for change in the parameter. This paper represents flexure micromotion stages with modular design. Compliance matrix method has been used for designing the flexure mechanism. Nonlinear 2-DOF model is used to characterize the stiffness of XY stage, maximum stress-induced. Proposed XY motion stage has a travel range of ±3.2 mm² with 0.12 mm parasitic error. Dynamic analysis is performed to determine modal frequency of the stage. Maximum error estimated in analytical and FEA model is 26.38%. Linear and nonlinear analytical results are compared with FEA and are in agreement.

1 Introduction

Compliant mechanism transmits motion by deformation of flexure elements. Mostly used flexure elements are blade flexure and wire flexure or slender rod [1]. Flexure elements are arranged in series or parallel. In series arrangement two or more 1-DOF are connected to obtain desired motion and motion can be controlled at the expense of high inertia, low natural frequency, and cumulative errors [2, 3]. Parallel mechanism has advantages of high payload capacity, lower inertia, and high natural frequency [4]. However, the parallel mechanism has disadvantages such as low workspace and parasitic error. Flexure parallel stage is used in many applications in precise machines and instruments. Compact XY Flexure parallel stage with a large motion range is desirable in many applications, atomic force microscopy, MEMS, biomedical implant and space application [3, 5, 6]. They are used in various applications because of no backlash, free of friction, no noise emission and no need for lubrication [4]. Designing the flexure mechanism has some challenges because of its nonlinear behavior, lack of motion range and cross-axis coupling [7]. Flexure parallel stages are mostly driven by piezoelectric or electromagnetic actuators. Stages driven by piezoelectric actuator has small motion range, high stiffness and compactness and those driven by electromagnetic actuator have large workspace, low stiffness, and ease to vibrate [2]. Compliance matrix method as reported in [1–4, 8–13] has been used for designing the micromotion stage.

In the literature, many parallel flexure mechanisms have been proposed and analyzed. Herpe et al. [14] presented a model used to characterize micromotion stage. Two-DOF nonlinear model is used to characterize force-displacement and stress analysis. Dynamic analysis is carried to find natural frequency of stage. The proposed mechanism has motion range of ±2.3 with parasitic error of 60 micron. Awtar [10] in his Ph.D. thesis presented analytical formulation including geometric nonlinearity for family of symmetric XY Flexure mechanism with a large workspace and small parasitic error. Pham et al. [9] address the stiffness models based on the way flexure elements are connected together. Awtar et al. [11] presented a nonlinear force-displacement model for 2-D beam flexure. Su et al. [15] presented a screw theory approach for synthesis and analysis of compliant joint. Li et al. [3] presented the idea of totally decoupling and analyzed double parallelogram flexure using matrix method for modeling compliance and stiffness. Wan et al. [12] presented a survey of recently developed flexure mechanisms with large motion range and greater accuracy. Su et al. [1] presented symbolic formulation for compliance and synthesis of mechanism with serial, parallel and hybrid topologies based on screw theory. Jia et al. [16] presented a parameterized compliance approach for synthesis and analysis of flexure. Xu et al. [2] proposed new multistage compound parallelogram flexure. The motion range of the mechanism is greater than 10 mm.

In this paper, modular design for a flexure parallel stage is presented. Many monolithic micromotion stages have been discussed in the literature. Monolithic design does not require assembly of component however when flexures are deformation beyond yield strength they get fractured. This, in turn, led to remanufacturing of whole mechanism due to its monolithic nature. Clearly, there is the motivation for design of modular micromotion stage. Modular design helps in manufacturing and assembly all the components separately. Modular design has an advantage that parameters of flexure element can be varied to some extent and fabrication can be done at relatively low cost. The flow of this paper is as follows. Section 2 determines stiffness of motion stage. Sections 3 and 4 consider nonlinear force-displacement and maximum stress analysis. Section 5 determines the resonant frequency of the stage. The coupling analysis of stage is carried out in Sect. 6. Section 7 compares the analytical solution with FEA and finally conclusions are drawn.

2 Stiffness of Mechanism

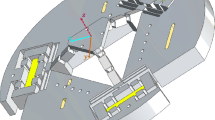
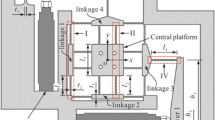
Let us consider a general twist $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} = \left( {\delta_{x} ,\;\delta_{y} ,\;\delta_{z} ,\;\theta_{x} ,\;\theta_{y} ,\;\theta_{z} } \right)$ and general wrench $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F} = \left( {F_{x} ,\;F_{y} ,\;F_{z} ,\;M_{x} ,\;M_{y} ,\;M_{z} } \right)$ [8] with 6 DOF (degree of freedom) at reference point OXYZ. The parameters of a beam are shown in Fig. 1. The dimensions and configuration of the XY motion stage are shown in Fig. 2 and CAD model is shown in Fig. 3. Mechanism consist of four rigid blocks located at corners are fixed. There are four intermediate blocks (P, Q, R and S) where input force is applied and a motion stage (C) at the center.

Fig. 1

Beam parameters [2]

Fig. 2

Spring equivalent model [14]

Fig. 3

CAD model

All flexure elements are numbered 1–16 have the same dimension and are given in meter.

According to linear elastic theory, the relation between twist and wrench can be written as in

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{F} = S_{\text{fix}} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} $$

(1)

where $S_{\text{fix}}$ is 6 × 6 stiffness matrix of fix-guided beam which is given as

$$ \left( {\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ {F_{z} } \\ {M_{x} } \\ {M_{y} } \\ {M_{z} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\frac{\text{EA}}{L}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{{12{\text{EI}}_{z} }}{{L^{3} }}} & 0 & 0 & 0 & {\frac{{6{\text{EI}}_{z} }}{{L^{2} }}} \\ 0 & 0 & {\frac{{12{\text{EI}}_{y} }}{{L^{3} }}} & 0 & { - \frac{{6EI_{y} }}{{L^{2} }}} & 0 \\ 0 & 0 & 0 & {\frac{\text{GJ}}{L}} & 0 & 0 \\ 0 & 0 & { - \frac{{6{\text{EI}}_{y} }}{{L^{2} }}} & 0 & {\frac{{4{\text{EI}}_{y} }}{L}} & 0 \\ 0 & {\frac{{6{\text{EI}}_{z} }}{{L^{2} }}} & 0 & 0 & 0 & {\frac{{4{\text{EI}}_{z} }}{L}} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\delta_{x} } \\ {\delta_{y} } \\ {\delta_{z} } \\ {\theta_{x} } \\ {\theta_{y} } \\ {\theta_{z} } \\ \end{array} } \right) $$

(2)

where E and G is Young’s modulus and shear modulus, respectively, A = t × w is beam’s cross-section area, L is length of beam, J is torsion constant and $I_{z} = \frac{{w \times t^{3} }}{12}$ and $I_{y} = \frac{{t \times w^{3} }}{12}$ are the area moments [1]. This matrix is at local frame which needs to be shifted to global frame by using the shifting law from screw theory and presented in [5, 6, 13, 14, 17, 18]. This is implemented by pre multiplying by inverse of (Tr) transpose and post multiplying by inverse of (Tr) to $S_{\text{fix}}$ as follows.

$$ S_{i}^{j} = \left( {\text{Tr}} \right)_{i}^{{j^{ - T} }} \cdot S_{\text{fix}} \cdot \left( {\text{Tr}} \right)_{i}^{{j^{ - 1} }} $$

(3)

where ‘i’ is local reference of beam and ‘j’ is global reference at the center of motion stage. T is the transpose of matrix and $\left( {\text{Tr}} \right)_{i}^{j}$ is 6 × 6 adjoint transformation matrix given as

$$ \left( {\text{Tr}} \right)_{i}^{j} = \left[ {\begin{array}{*{20}c} {R_{i}^{j} } & {S\left( {t_{i}^{j} } \right)R_{i}^{j} } \\ 0 & {R_{i}^{j} } \\ \end{array} } \right] $$

(4)

Owing to symmetry stiffness of mechanism can be evaluated from the stiffness of one-quarter part of parallelogram, i.e. parallelogram 1–2–3–4. The stiffness of beam 1 at center C is given by $S_{1}^{c}$ It can be obtained by translating along X by 0.03 and Y direction by (L + 0.03) and zero in Z direction. Therefore, $t_{1}^{C} = |0.03, - (L + 0.03),0|$.

$$ S_{1}^{c} = \left( {\text{Tr}} \right)_{1}^{{c^{ - T} }} \cdot S_{\text{fix}} \cdot \left( {\text{Tr}} \right)_{1}^{{c^{ - 1} }} $$

(5)

The stiffness of flexure 2 at center C is obtained by revolving flexure 1 about Y-axis by π radians with no translation as given below.

$$ S_{2}^{C} = {\text{Ry}}\left( \pi \right)_{2}^{{C^{ - T} }} \cdot S_{1}^{C} \cdot {\text{Ry}}\left( \pi \right)_{2}^{{C^{ - 1} }} $$

(6)

Similarly, stiffness of flexure 3 at point C can be obtained by revolving the flexure 1 by −π/2 rad about Z-axis and translating 0.02 in X direction 0.03 in Y direction and zero in Z direction. Hence $t_{3}^{C} = \left| {0.02, - 0.03,0} \right|$.

$$ S_{3}^{C} = ({\text{Tr}})_{3}^{{C^{ - T} }} \cdot S_{\text{fix}} \cdot ({\text{Tr}})_{3}^{{C^{ - 1} }} $$

(7)

Stiffness of flexure 4 is obtained by simply revolving flexure 3 by π radians about Y-axis.

$$ S_{4}^{C} = {\text{Ry}}\left( \pi \right)_{3}^{{C^{ - T} }} \cdot K_{3}^{C} \cdot {\text{Ry}}\left( \pi \right)_{3}^{{C^{ - 1} }} $$

(8)

The stiffness of the parallelogram 1–2–3–4 at center C is given as

$$ S_{C1} = \frac{1}{{\left( {S_{1}^{C} + S_{2}^{C} } \right)^{ - 1} + \left( {S_{3}^{C} + S_{4}^{C} } \right)^{ - 1} }} $$

(9)

The stiffness of mechanism can be obtained by rotating the parallelogram P by −π/2 around the Z-axis as follows.

$$ S = S_{C1} + S_{C2} + S_{C3} + S_{C4} $$

(10)

where $S_{C1} ,\;S_{C2} ,\;S_{C3} ,\;S_{C4}$ are stiffness of three-quarter of mechanism.

3 Nonlinear Modeling

Owing to large deformation, the length of beam flexure is not constant thus nonlinear analysis is considered. This nonlinearity is due to tension loading terms which cause the change in length of beam flexure. Each beam flexure is considered as spring connected to rigid body as shown in Fig. 2. Further it is assumed that parallelogram P and R can travel in only Y direction and parallelogram Q and S can travel only in X direction. Let us consider outer parallelogram i.e. beam 1–2, 5–6, 9–10, and 13–14 and inner parallelogram i.e. beam 3–4, 7–8, 11–12, and 15–16. From Fig. 2, the deformation at the intermediate stage is written as

$$ \left\{ {\begin{array}{*{20}c} {\delta_{\text{Py}} = \delta_{1y} = \delta_{2y} } \\ {\delta_{\text{Ry}} = \delta_{9y} = \delta_{10y} } \\ {\delta_{\text{Qx}} = \delta_{5x} = \delta_{6x} } \\ {\delta_{\text{Sx}} = \delta_{13x} = \delta_{14x} } \\ \end{array} } \right. $$

(11)

The reaction forces at the intermediate stage are written as follows.

$$ \left\{ {\begin{array}{*{20}c} {F_{\text{Py}} = F_{1y} + F_{2y} } \\ {F_{\text{Ry}} = F_{9y} + F_{10y} } \\ {F_{\text{Qx}} = F_{5x} + F_{6x} } \\ {F_{\text{Sx}} = F_{13x} + F_{14x} } \\ \end{array} } \right. $$

(12)

where $F_{\text{Py}}$ represent reaction force at intermediate stage p in y direction, $F_{1y}$ is reaction force in beam 1 and so on. As in [14] the total stiffness of parallelogram 1–2, 5–6, 9–10 and 13–14 can be derived by considering a single beam as shown in Fig. 3.

Fig. 4

Deformed condition of beam 1 [1]

The downward bending force as given in on beam 1 is given by

$$ F_{{1y{\text{bend}}}} = \frac{{12{\text{EI}}_{z} \delta_{1y} }}{{L_{1}^{3} }} $$

(13)

where $\delta_{1y}$ is a deflection of beam 1. The component of the tensile force in Y direction is given by

$$ F_{{1y{\text{tens}}}} = {\text{EA}} \in_{1} \;\sin \; \propto_{1} $$

(14)

where $\in_{1} \; = \;\left( {L_{\text{tens}} - L} \right)/L$ is linear strain and $\propto_{1} \; = \;\tan^{ - 1} (\delta_{1} /L)$ is the angle made by beam 1 with horizontal. Therefore, total force acting on beam 1 along the Y-axis is given by

$$ F_{1y} = F_{{1y{\text{bend}}}} + F_{{1y{\text{tens}}}} $$

(15)

Now taking into consideration inner structure the stiffness can be obtained by considering one outer beam connected with single inner one as shown in Fig. 5. For small deflection of beam 16 there is a very small deflection of beam 14, therefore, stiffness of beam 14 is negligible as compared to stiffness of beam 16. The force acting along the X-axis on beam 16 can be obtained as

Fig. 5

Spring model of perpendicular elements

$$ F_{16xT} = \frac{{12{\text{EI}}_{z} \delta_{14x} }}{{L_{14}^{3} }} + \frac{{{\text{EA}} \cdot L_{14} \sin \;\alpha_{14} }}{{L_{14} }} $$

(16)

The force acting along the Y-direction is, therefore, a combined effect of the forces applied by beams 14 and 16 as given.

$$ F_{16y} = \frac{{F_{16xT} \delta_{16y} }}{{L_{16x} }} + \frac{{12{\text{EI}}_{z} \delta_{16y} }}{{L_{16}^{3} }} $$

(17)

Therefore, the reaction forces at the center C motion stage due to δ_Cx and δ_Cy are

$$ F_{\text{Cx}} = F_{\text{Qx}} + F_{\text{Sx}} + F_{3x} + F_{4x} + F_{11x} + F_{12x} $$

(18)

$$ F_{\text{Cy}} = F_{\text{Py}} + F_{\text{Ry}} + F_{7y} + F_{8y} + F_{15y} + F_{16y} $$

(19)

The deflection at the intermediate stage is related to the deflection of the center of the motion stage. The following equation can be deducted by applying Pythagoras theorem to deformed and undeformed conditions between intermediate and motion stages.

$$ \left\{ {\begin{array}{*{20}c} {\delta_{\text{Py}} = \delta_{Cy} - \left( {L - \sqrt {L^{2} - \delta_{\text{Cx}}^{2} } } \right)} \\ {\delta_{\text{Ry}} = \delta_{Cy} + \left( {L - \sqrt {L^{2} - \delta_{\text{Cx}}^{2} } } \right)} \\ {\delta_{\text{Qx}} = \delta_{Cx} - \left( {L - \sqrt {L^{2} - \delta_{\text{Cy}}^{2} } } \right)} \\ {\delta_{\text{Sx}} = \delta_{Cx} + \left( {L - \sqrt {L^{2} - \delta_{\text{Cy}}^{2} } } \right)} \\ \end{array} } \right. $$

(20)

4 Stress Analysis

Stresses in the XY mechanism are determined to know allowable displacement the stage can undergo within the elastic limit of the material. The maximum stress occurs at one of the corner of flexure beam where it is attached to rigid body. Maximum Bending stress in beam is given by σ_max = M_bY/I. Where Y is the farthest point from neutral axis (half of beam thickness) and M_b= F_{1y_tens} × 0.5 × L. From Eq. (13), maximum bending stress can be given by.

$$ \sigma_{{1{\text{bend}}}} = \frac{{3{\text{Ew}}\delta_{1y} }}{{L_{1}^{2} }} $$

(21)

Also, stress induced due to tensile loading in beam 1 is given by

$$ \sigma_{{1{\text{tens}}}} = E \in_{1} $$

(22)

From Eqs. (23) and (24) we can write maximum stress is

$$ \sigma_{1} = K_{1} \sigma_{{1{\text{bend}}}} + K_{2} \sigma_{{1{\text{tens}}}} $$

(23)

where K₁ is a stress concentration factor for bending loading and K₂ is the stress concentration factor for tensile loading.

5 Dynamic Analysis

Dynamic analysis helps in finding the resonance frequency of mechanism. The equation of motion for un-damped free vibration is given.

$$ {\text{M}}\;{\ddot{\text{x}}} + {\text{S}}\;{\dot{\text{x}}} = 0 $$

(24)

where M is mass matrix and K is a stiffness matrix of mechanism. The mass matrix is given by

$$ \left[ {\begin{array}{*{20}c} {M_{\text{xx}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {M_{\text{yy}} } & 0 & 0 & 0 & 0 \\ 0 & 0 & {M_{\text{zz}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {I_{\text{xx}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {I_{\text{yy}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {I_{\text{zz}} } \\ \end{array} } \right] $$

(25)

where $M_{\text{xx}} ,\;M_{\text{yy}} ,\;{\text{and}}\;M_{\text{zz}}$ are moving mass in X, Y, and Z direction respectively $I_{\text{xx}} ,\;I_{\text{yy}} \;{\text{and}}\;I_{\text{zz}}$ are the moment of inertia about X, Y and Z direction, respectively.

$$ M_{\text{xx}} = M_{\text{yy}} = m_{0} + 2m_{p} + \left( {8 \times \frac{33}{140}m_{\text{beam}} } \right) + \left( {4 \times m_{\text{beam}} } \right) $$

(26)

where mass of motion stage $m_{0} = 0.06^{2} \times W \times \rho$, mass of parallelogram $m_{p} = 0.06 \times 0.02 \times \rho$, mass of beam $m_{\text{beam}} = W \times t \times L \times \rho$

$$ M_{\text{zz}} = m_{0} + \left( {8 \times \frac{33}{140}m_{\text{beam}} } \right) $$

(27)

$$ I_{\text{xx}} = I_{\text{yy}} = \frac{{m_{0} \left( {0.06^{2} + w^{2} } \right)}}{12} + 2m_{p} \left( {\frac{{0.02^{2} + w^{2} }}{12} + \left( {L + 0.03} \right)^{2} + \frac{{0.06^{2} + w^{2} }}{12}} \right) $$

(28)

$$ I_{\text{zz}} = 4m_{p} \left( {\frac{{0.06^{2} + 0.02^{2} }}{12}} \right) + m_{0} \left( {\frac{{0.03^{2} + 0.03^{2} }}{12}} \right) $$

(29)

The resonance frequency of stage can be determined by

$$ f = \frac{1}{2\pi }\sqrt {\frac{S}{M}} $$

(30)

6 Coupling Analysis

The parasitic error in flexure mechanism is due deformation of intermediate stage P and R when input displacement is applied to intermediate stage Q and S. This error is also called cross-coupling. The parasitic error in the X direction can be determined by subtracting the resulting displacement δ_Sx of parallelogram S from desired output displacement δ_Cx as follows [14].

$$ \delta_{{x\_{\text{par}}}} = \delta_{\text{Cx}} - \delta_{\text{Sx}} $$

(31)

Similarly, the parasitic error in Y direction can be determined by subtracting resulting displacement $\delta_{\text{Ry}}$ of parallelogram R from desired output displacement $\delta_{\text{Cy}}$ as follows.

$$ \delta_{{y\_{\text{par}}}} = \delta_{\text{Cy}} - \delta_{\text{Ry}} $$

(32)

7 FEA Validation

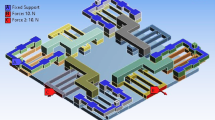
The analytical model is validated using ABAQUS 6.14 software. The parameters of the beam and material properties are given in Table 1.

Table 1 Parameters of beam

7.1 Force-Displacement Analysis

The force-displacement relation is studied by applying gradual displacement of 3.25 mm at one of the intermediate stage and reaction forces are noted. Nonlinear behavior is due to the load stiffening phenomenon at lager displacement. The force required for 3.25 mm displacement is 166.7 N analytically and 190.5 N from FEA. Thus the nonlinear analytical model is validated. Comparing the result of analytical model for linear (Eq. 10) and nonlinear (Eq. 21) behavior and FEA shows some linearity for small deflection and deviates for large displacement. These results are shown in Fig. 6.

Fig. 6

Force-displacement plot

7.2 Stress Analysis

In order to study the stress variation in mechanism, the stress concentration factor K1 is taken as 1 and K2 is taken as 2 as in [14]. The maximum displacement evaluated from the analytical model is 4.3% smaller than FEA analysis. The error in the FEA and analytical model is 26.38%. Figure 7 show that yield strength of material has reached 5 mm displacement.

Fig. 7

Stress displacement plot

7.3 Coupling Analysis

Coupling analysis is carried to determine maximum positioning error in model. In FEA displacement is applied in Y direction at center of motion stage in steps and output displacement is recorded in at intermediate stage S in X direction. The parasitic displacement plot is shown in Fig. 8. Maximum parasitic error is 0.12 mm from FEA and error in analytical and FEA is 2%.

Fig. 8

Parasitic error

7.4 Modal Analysis

Frequency analysis is done in ABAQUS 6.14 using Lanczos Eigen solver. The first four mode shapes are shown in Fig. 9. The first two resonant frequencies in X and Y directions are the same and occur at 27.9 Hz form FEA and 26.7 Hz analytically. The third resonant frequency occurs at 125.15 Hz from FEA and 134.4 Hz analytically. Fourth frequency from FEA is 261.8 and 285.2 Hz analytically. The error in analytical and FEA model is 9.24%.

Fig. 9

Mode shapes of mechanism

8 Conclusion

An analytical model incorporating linear and nonlinear behavior was presented. MATLAB was used to characterize the compliant XY stage. Analytical model was successfully applied to predict stiffness, motion range considering the limitation such as maximum stress. The model proposed can predict the output displacement as input displacement is applied. Its micromotion stage is used for position control accurately. The results from FEA and analytical model are within 26.38%. The micromotion stage has a travel range of ±3.2 mm with cross-coupling of 0.12 mm. The yielding occurs at the displacement of 5 mm. The ratio between the first two frequencies and third is greater than 0.22. Modular design can be successfully applied to micromotion stage. Modular design will greatly reduce the manufacturing cost for the same characterization of a monolithic structure.