Keywords

1 Introduction

Thin circular steel plates are widely used in the fabrication of steel structures such as cylindrical pressure vessels, storage containers in oil and gas companies, maritime and aerospace industry. While in service, these circular steel plates are subjected to mechanical loads and temperature variations leading to thermo-mechanical loads. As a result, the plates will undergo deformations due to buckling loads. A simple approach to increase the buckling strength of the steel plate is to increase its thickness. However, increasing the thickness of the plate proportionately increases the weight and cost of the structure. Hence, to increase the buckling resistance, generally, stiffeners are attached on the face of the plates. For stiffeners, commercially available steel sections with standard geometric shapes like T, I and HAT are chosen from the open market. Reinforcement of plates with stiffeners increases the buckling strength without adding much to the self-weight for the structure.

Estimation of the buckling strength of a thin plate is possible through analytical solutions. But, it becomes difficult to determine the buckling load when stiffeners are attached to the plate. Therefore, one has to resort to either experiments or numerical simulations. It is known that conducting experiments is not only expensive but also time-consuming process. On the other hand, finite element-based numerical simulation offers a great advantage to incorporate a variety of stiffeners and boundary conditions. These simulations can be repeated several times to investigate the effect of different parameters. In the present investigation, it is proposed to determine the buckling load of a circular steel plate with three different stiffeners attached to the face of the plate through numerical simulations. For this purpose, Abaqus is employed, which is one of the powerful FE-based software tools for numerical simulations.

2 Literature Review

From the published literature, most pertinent studies conducted by the previous investigators are presented here to give a brief background. Rossettos and Yang [1] presented a treatment of asymmetric buckling problem of ring-stiffened circular plates. They indicated a coalescence of the lowest symmetric and asymmetric mode eigenvalues involving ring torsional stiffness. Grondin et al. [2] conducted a parametric study on buckling of stiffened steel plates. They considered the stability of stiffened plates using a finite element model. In their study, T -shaped stiffeners are used for buckling analysis and parameters included are (1) initial plate imperfections, (2) direction and magnitude of residual stresses, (3) slenderness ratio of the plate, (4) aspect ratio of the plate and (5) cross-sectional area ratio of plate to the stiffener.

Ma and Wang [3] investigated nonlinear bending and post-buckling of a functionally graded circular plate under direct mechanical and thermal loads. They used classical nonlinear von Karman plate theory, for axisymmetric large deflection and bending of a functionally graded circular plate. The types of loads considered in their investigation are mechanical, thermal and combined thermal–mechanical. Brubak and Hellesland [4] conducted an approximate buckling strength analysis for plates reinforced with stiffeners with arbitrary orientation. Ding and Lee [5] gave an analytical solution for a circular plate that is uniformly loaded and clamped at the edges.

Modarresi and Showkati [6] experimentally investigated the failure of diagonally stiffened circular plates to determine ultimate bending capacity. In their experiments, to strengthen the plate, two types of shallow and deep stiffeners of reverse L and rectangular cross sections were attached. They considered simply supported and clamped edge boundary conditions for a circular plate subjected to lateral loads up to their final collapse. They compared experimental results with the nonlinear analysis of stiffened circular plates using FEM. The results are presented through load–deflection and load–strain curves and volumetric charts. Finally, it was concluded that increasing the height of the diagonal stiffener or changing its cross-sectional shape may not be an effective way of increasing the load-bearing capacity of the diagonally stiffened circular plates. It was recommended that, instead of using one diagonal stiffener, it is better to use two perpendicular diagonal stiffeners with the same amount of steel as the first one.

Rao and Rao [7] presented an exact solution for elastic buckling of circular plates resting on internal elastic ring support and elastically restrained against translation at the outer edge. They used classical plate theory to solve the governing differential equations. Further, they introduced a Mathematica code to estimate the buckling load. Tran et al. [8] studied the buckling behaviour of stiffened curved panels under uniform longitudinal compression to address the linear buckling and the ultimate strength of panel which are both influenced by the combined effect of curvature and stiffening. They finally proposed a design methodology for stiffened flat plates to be adopted by European Standards. They concluded that the plate curvature has to be taken into consideration to optimize the design.

Daniel [9] attempted the stability problem of thin circular plates that are stiffened with a thin cylindrical shell on the circumference and also on the plate. In his investigation, an attempt was made to determine the in-plane axisymmetric critical load with a view to show the effect of cylindrical shell stiffener. Daniel [10] summarized the differential equations for the stability of shell-stiffened circular plates and shell-stiffened annular plates assuming the deformations are axisymmetric. Yu et al. [11] focused their attention on the uniaxial ultimate compressive strength of stiffened panels with openings. In their work, experiments were conducted on longitudinal stiffened panels with rectangular openings applying combined loads. Numerical simulations were carried out on stiffened panels considering large elastoplastic deformation behaviour using Abaqus.

From the literature review, it is found that there are a very few papers, but not too many, focusing on the buckling of stiffened circular plates. But, investigations concerning the buckling load as a function of the plate aspect ratio, particularly when the plate is stiffened, are very much limited in the open literature. Therefore, in the present investigation it is proposed to determine the effect of aspect ratio on the buckling load of a stiffened circular plate using the protocols specified in the user’s manual of Abaqus 6.5 [12].

3 Analytical Solution

In process industry, thin circular plates are subjected to in-plane radial compressive forces from the supporting structure when there is a change in the working temperature of the medium. As a result, buckling of the circular plates can take place. In the following section, governing differential equations for plates subjected to buckling loads are presented.

Circular plate subjected to uniformly distributed in-plane compressive radial forces:

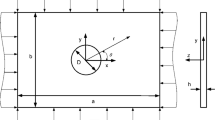
As shown in Fig. 1, in the present analysis, a circular plate is considered that is subjected to in-plane radial compressive forces (qr). In the buckling analysis, we include only axisymmetric geometries such as circular plates. Thus, we can use the polar coordinate system represented by r and Ø. Equation (1) that represents buckling of a rectangular plate can be transformed into a circular plate for convenience of analysis.

Fig. 1
figure 1

Circular plate subjected to uniformly distributed in-plane compressive radial forces

Full size image
$$ \frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{x}}^{4} }} + 2\frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{x}}^{2} \partial {\mathbf{y}}^{2} }} + \frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{y}}^{4} }} = \frac{1}{{\mathbf{D}}}\left( {{\mathbf{N}}_{{\mathbf{x}}} \frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{x}}^{2} }} + 2{\mathbf{N}}_{{{\mathbf{xy}}}} \frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{x}}\partial {\mathbf{y}}}} + {\mathbf{N}}_{{\mathbf{y}}} \frac{{\partial^{4} {\mathbf{w}}}}{{\partial {\mathbf{y}}^{4} }}} \right) $$
(1)

For a specific case, when the structure is in equilibrium, for an axisymmetric loading condition,we have

$$ {\mathbf{Nx}}\, = \,{\mathbf{Ny}}\, = \,{\mathbf{Nr}}\, = \, - {\mathbf{qr}}, \, {\mathbf{Nxy}}\, = \,{\mathbf{0}} $$
(2)

Denoting

$$ \varvec{\mu}^{2} = \frac{{\varvec{q}_{\varvec{r}} }}{\varvec{D}} $$
(3)

and using the relations between the polar and Cartesian coordinates, we can derive an equation for axisymmetric circular plate subjected to a circumferential compressive force as shown in Fig. 1, as given below.

$$ \frac{{{\text{d}}^{4} \varvec{w}}}{{{\text{d}}\varvec{r}^{4} }} + \frac{2}{\varvec{r}}\frac{{{\text{d}}^{3} \varvec{w}}}{{{\text{d}}\varvec{r}^{3} }} - \frac{1}{{\varvec{r}^{2} }}\frac{{{\text{d}}^{2} \varvec{w}}}{{{\text{d}}\varvec{r}^{2} }} + \frac{1}{{\varvec{r}^{3} }}\frac{{{\text{d}}\varvec{w}}}{{{\text{d}}\varvec{r}}} +\varvec{\mu}^{2} \left[ {\frac{{{\text{d}}_{\varvec{w}}^{2} }}{{{\text{d}}\varvec{r}^{2} }} + \frac{1}{\varvec{r}}\frac{{{\text{d}}\varvec{w}}}{{{\text{d}}\varvec{r}}}} \right] = 0 $$
(4)

Now, let us introduce the following new variable:

$$ {\varvec{\uprho}} = {\mathbf{\mu r}} $$
(5)

that denotes a non-dimensional polar radius. By means of new variable ρ, it is possible to rewrite Eq. (4), into the form of Eq. (6).

$$ \frac{{{\text{d}}^{4} \varvec{w}}}{{{\text{d}}\varvec{\rho}^{4} }} + \frac{2}{\varvec{\rho}}\frac{{{\text{d}}^{3} \varvec{w}}}{{{\text{d}}\varvec{\rho}^{3} }} + \left( {1 - \frac{1}{{\varvec{\rho}^{2} }}} \right)\frac{{{\text{d}}^{2} \varvec{w}}}{{{\text{d}}\varvec{\rho}^{2} }} + \frac{1}{\varvec{\rho}}\left( {1 + \frac{1}{{\varvec{\rho}^{2} }}} \right)\frac{{{\text{d}}\varvec{w}}}{{{\text{d}}\varvec{\rho}}} = 0 $$
(6)

Equation (6) is a linear fourth-order, homogeneous differential equation. The general solution for Eq. (6) is

$$ \varvec{w}\left(\varvec{\rho}\right) = \varvec{C}_{1} + \varvec{C}_{2} \ln\varvec{\rho}+ \varvec{C}_{3} \varvec{J}_{0} \left(\varvec{\rho}\right) + \varvec{C}_{4} \varvec{Y}_{0} \left(\varvec{\rho}\right) $$
(7)

where J0(ρ) is Bessel’s function of the first kind and Y0(ρ) is Bessel’s function of the second kind both for zeroth order. In Eq. (7), C1, C2, C3 and C4 are constants of integration. Since w(ρ) must be finitely quantified for all values of ρ, including ρ = 0, then the two terms with ρ and Y0(ρ), having singularities at ρ = 0, must be dropped for the solid plate because they approach infinity, when ρ = 0. Thus, for the solid circular plate, Eq. (7) must be taken in the form

$$ \varvec{w}\left(\varvec{\rho}\right) = \varvec{C}_{1} + \varvec{C}_{3} \varvec{J}_{0} \left(\varvec{\rho}\right) $$
(8)

to determine the critical buckling loads qr. These loads are assumed to be acting at the mid-plane of the circular plate.

4 Finite Element Modelling

FE modelling of the plate with T, I and HAT stiffeners is carried out using Abaqus software version 6.5. From Abaqus library, a four-node, doubly curved, linear shell element is selected for the geometric modelling of the structure under consideration. To maintain an acceptable aspect ratio for the element, shell elements were preferred over three-dimensional elements. The choice of the shell elements will also ensure a reasonable mesh density. Stiffeners of three different geometric shapes T, I and HAT are chosen for reinforcement of the circular plate. As shown in Fig. 2, on each plate any one type of ring stiffeners is placed at three different radial locations, the first one at 0.1 m, the second one at 0.25 m and the third one at 0.4 m. Mild steel properties are chosen for plate and stiffeners during the analysis. The in-plane compressive load of 20 kN is considered acting on the circular plate with stiffeners. As shown in Fig. 3, loading and the boundary conditions are such that the plate is fixed along the edge while released in the radial direction. Abaqus 6.5 is employed to carry out FE analysis on the structure under consideration.

Fig. 2
figure 2

Circular plate with three commercially available stiffener sections

Full size image
Fig. 3
figure 3

Loading and the boundary conditions for stiffened circular plate

Full size image

In the present numerical simulations, radius of the circular plate is fixed at 0.5 m. The thickness of the plate is varied such that the radius-to-thickness (R/T) ratio is in the range of 200–250 with an increment of 10 each. Height and thickness of the stiffeners are held constant at 0.007 m and 0.002 m, respectively.

Material Properties of Mild Steel:

Young’s modulus E = 200 GPa,

Poisson’s ratio = 0.3.

5 Results and Discussion

The results of the simulation studies to determine the buckling load of the stiffened circular plate as a function of aspect ratio in the range of investigation from 200 to 250 in steps of 10 are presented in Tables 1, 2 and 3. It is observed that for a given mode of deformation the buckling load decreases with the increase of aspect ratio. It is also observed that for any given aspect ratio in the range of investigation, the buckling load increases with the progressive mode of deformation from mode-1 to mode-6. Further, the plate with T-shaped stiffener has the lowest buckling strength for all aspect ratios and all modes of deformation. The plate with HAT-shaped stiffener showed the largest buckling load for all conditions. The plate with I-shaped stiffener has larger buckling loads compared to the plate with T-shaped stiffeners but marginally less buckling load when compared to the plate with HAT-shaped stiffeners. However, the buckling loads for I-shaped and HAT-shaped stiffeners are closely comparable to each other. One set of results on buckling loads of plate with T-, I- and HAT-shaped stiffeners are presented in Table 4 for comparison. Typical shapes of deformation of plates with T-, I- and HAT-shaped stiffeners are shown in Figs. 4, 5 and 6, respectively.

Table 1 Buckling load of the circular plate with T stiffener under different modes for various R/T ratios
Full size table
Table 2 Buckling load of the circular plate with I stiffener under different modes for various R/T ratios
Full size table
Table 3 Buckling load of the circular plate with HAT stiffener under different modes for various R/T ratios
Full size table
Table 4 Buckling load of circular plates with stiffeners of different geometric shapes
Full size table
Fig. 4
figure 4

Deformed shape of the circular plate with T-shaped stiffener

Full size image
Fig. 5
figure 5

Deformed shape of the circular plate with I-shaped stiffener

Full size image
Fig. 6
figure 6

Deformed shape of the circular plate with HAT-shaped stiffener

Full size image

From the results in Figs. 7, 8 and 9, it is observed that the buckling load curves of the stiffened circular plates are seen in pairs. Buckling load curves for mode-1 and mode-2 are close to each other and appear like a pair of curves. Likewise, buckling load curves for mode-3 and mode-4, and mode-5 and mode-6 formed another two pairs of curves. This observation is consistent for all three types of stiffeners considered in the present investigation. Figures 10 and 11 show the variation of buckling load as a function of plate aspect ratio for T, I and HAT stiffeners in mode-1 and mode-2, respectively. It is further observed that there is not much of a difference between buckling loads for plates with I and HAT stiffeners.

Fig. 7
figure 7

Buckling load of circular plate with T stiffener under different modes for various R/T ratios

Full size image
Fig. 8
figure 8

Buckling load of circular plate with I stiffener under different modes for various R/T ratios

Full size image
Fig. 9
figure 9

Buckling load of circular plate with HAT stiffener under different modes for various R/T ratios

Full size image
Fig. 10
figure 10

Buckling load of circular plates in mode-1, with stiffeners of different geometric shapes

Full size image
Fig. 11
figure 11

Buckling load of circular plates in mode-2, with stiffeners of different geometric shapes

Full size image

6 Conclusions

In the present investigation, buckling load for stiffened circular plates is presented for six modes of deformation as a function of plate aspect ratio in both tabular and graphical forms. From the present analysis, it is found that the circular plate with HAT-shaped stiffener offers highest buckling strength. The plate with T-shaped stiffener offers lowest buckling strength. However, the plate with I-shaped stiffener offered buckling strength in between the plates with T- and HAT-shaped stiffeners. Further, the buckling strength of plates with HAT-shaped and I-shaped stiffeners is closely comparable. It is concluded that the geometric shape of the stiffener is very important since it can affect the buckling load and overall buckling behaviour of the plate considerably. Through this investigation, the capabilities of Abaqus software are demonstrated to determine buckling loads of stiffened plates. It is understood that the predictive capabilities of the numerical models and software tools greatly depend on the proper definition of the problem and well-defined boundary conditions specific to a problem.