Keywords

1 Introduction

Vehicle routing problem has been extensively studied since it was proposed. Fleet size and mix vehicle routing problem with time windows (FSMVRPTW) is an important branch of vehicle routing problem. It refers to the use of a group of different types of fleets to deliver services to fixed customers, and to solve the minimum cost required to complete tasks under the conditions of meeting time window constraints and vehicle capacity constraints. Because the heterogeneity of fleet and the constraints of time windows are closer to real life, the research of FSMVRPTW is of great significance. FSMVRPTW has many application scenarios in real life, such as logistics distribution, school bus routing planning and so on. Good routing can not only save transportation costs and improve distribution efficiency, but also improve service quality, bringing lucrative profits to the market.

The vehicle routing problem is a NP-hard problem, and it is difficult to find the exact solution, so many heuristic algorithms are produced for solving it. Golden [1] described several effective methods to solve FSMVRP, and provides some benchmark problems for future research. Liu and Shen [2] summarized the previous algorithms of FSMVRP and VRPTW. They drew a conclusion that the traditional sequential routing construction method for VRPTW is not suitable for heterogeneous fleet problems, while using parallel routing construction method to solve FSMVRPTW itself is a difficult task. Several insertion-based saving heuristic algorithms are also proposed. Mauro [3] presented a constructive heuristic algorithm and a meta-heuristic algorithm to solve FSMVRPTW. A constructive heuristic algorithm is implemented by first generates an incomplete solution as the initial solution, and then uses parallel insertion algorithm to insert the remaining nodes. Based on the construction of heuristic algorithm, meta-heuristic algorithm uses ruin strategy to eliminate part of the routing and rebuild procedure to reconstruct the routing. Olli [4] presented a deterministic annealing heuristic algorithm. The algorithm consists of three stages. In the first stage, the initial solution is generated by combining diversification strategy with learning mechanism. In the second stage, local search process is used to reduce the number of routes in the initial solution. In the third stage, the solution is further improved by a set of four local search operations embedded in the deterministic annealing framework. Repoussis and Tarantilis [5] obtained a new adaptive memory programming (AMP) method for solving FSMVRPTW. This method consists of a probabilistic semi-parallel construction heuristic algorithm, a new solution reconstruction mechanism, an innovative iterative tabu search algorithm for enhancing local search and a frequency-based long-term storage structure. Vidal [6] proposed a hybrid genetic search algorithm with advanced diversity control for a class of vehicle routing problems with large time constraints. The algorithm achieves satisfactory results in dealing with various complex vehicle routing problems including time windows.

Ant colony optimization algorithm  [7] is a meta-heuristic algorithm which simulates ants’foraging behavior in nature. It has unique advantages in solving routing optimization problems. Ant colony algorithm has been widely studied and applied in solving TSP [8, 9], VRP [10, 11], VRPTW [12, 13], etc. But it has less research in FSMVRPTW. The main reason is that ants can choose the next node according to pheromone concentration, but there is no better solution to the choice of vehicle type. If the vehicle type is taken as a variable associated with the node coordinates, the search dimension will be improved, the search space will be greatly expanded, and the search efficiency will be reduced. If the vehicle type is chosen randomly when constructing feasible routing, the algorithm has some shortcomings such as inadequate searching ability and inability to find the optimal solution for cases with more vehicle types. This paper proposes a hybrid ant colony algorithm, which combines ant colony system and constructive heuristic algorithm. It can not only effectively help ants choose the right vehicle type in multi-vehicle environment, but also give full play to the advantages of ant colony algorithm with strong search ability.

This paper mainly includes the following sections: In Sect. 2, the FSMVRPTW is formulated; The Sect. 3 introduces an insertion heuristic algorithm; The Sect. 4 introduces ant colony system and hybrid algorithm combining the insertion heuristic algorithm; The Sect. 5 is numerical experiment, and the last part is the conclusion.

2 Mathematical Model of FSMVRPTW

2.1 Symbolic Description

The relevant symbols in the mathematical model are illustrated as follows:

  • \( V=N\bigcup 0\): The set of all customers. Where \(N={1,2,\cdots ,n}\) is the set of customers and 0 is the distribution center.

  • \(A=\{(i,j)|i,j\in V\}\): The arc set.

  • \({d_{ij}}\): The distance of arc (i, j).

  • \(q_i\): Quantity demanded of i.

  • \(s_i \): Service time required by customer i.

  • \([a_i,b_i]\): Time window for customer i to receive services.

  • H: The set of different vehicle types for service.

  • \(K=\{1,\cdots ,k,\cdots \}\): The set of distinct vehicles obtained by defining n vehicles of type h for each \(h\in H\).

  • \(Q_k\): The capacity of vehicle k.

  • \(F_k\): The fix-cost of vehicle k.

  • \({t_{ik}}\): The time when vehicle k arrives at customer i.

  • \(\tau _i\): The time when vehicle starts serving customer i.

  • \(\pi _k\): The return time of vehicle k to the distribution center.

    \({x_{ijk}} = \left\{ \begin{array}{l} 1,~if~ vehicle ~ k~passed ~through~ arc~ \left( {i,j} \right) \\ 0,~otherwise \end{array} \right. \)

    \({y_{ik}} = \left\{ \begin{array}{l} 1,~if~i~is~served~by~vehicle~k\\ 0,~otherwise \end{array} \right. \)

    \( {z_k} = \left\{ \begin{array}{l} 1,~if~vehicle~k~is~used\\ 0,~otherwise \end{array} \right. \)

2.2 Mathematical Formulation

The mathematical model of FSMVRPTW can be expressed as follows:

$$\begin{aligned} \min Cost = \sum \limits _k {{F_k}} + \sum \limits _{i,j \in A} {\sum \limits _k {{d_{ij}}{x_{ijk}}} } \end{aligned}$$
(1)

Subject to :

$$\begin{aligned} \sum \limits _{i \in V} {{d_i}{y_{ki}} \le {Q_k},~\forall k \in K} \end{aligned}$$
(2)
$$\begin{aligned} \sum \limits _{i \in V} {{y_{ki}} = 1,~\forall k \in K} \end{aligned}$$
(3)
$$\begin{aligned} \sum \limits _{i \in V\backslash \left\{ j \right\} } {{x_{ijk}} = {y_{kj}},~\forall arc(i,j) \in A,\forall k \in K} \end{aligned}$$
(4)
$$\begin{aligned} \sum \limits _{j \in V\backslash \left\{ j \right\} } {{x_{ijk}} = {y_{kj}},~\forall arc(i,j) \in A,\forall k \in K} \end{aligned}$$
(5)
$$\begin{aligned} \sum \limits _{i \in N} {{x_{i0k}} = \sum \limits _{j \in N} {{x_{0jk}} = 1,} }~ \forall k \in K \end{aligned}$$
(6)
$$\begin{aligned} {\tau _i} = \max \left\{ {{a_i},{t_{ik}}} \right\} ,~\forall i \in V,~\forall k \in K \end{aligned}$$
(7)
$$\begin{aligned} {t_{jk}} = {\tau _i} + {s_i} + {d_{ij}},~\forall arc( {i,j} ) \in A \end{aligned}$$
(8)
$$\begin{aligned} {t_{ik}} < {b_i},~\forall i \in V \end{aligned}$$
(9)

The objective function is to minimize the sum of vehicle fix-costs and routes distances. Constraint 2 means that the vehicle is not allowed to exceed its maximum capacity. Constraint 3 means that each customer can only be accessed once. Constraint  4 and 5 ensure that no loops are generated within the routing. Constraint 6 indicates that the starting and ending position of the vehicle must be the distribution center, and Constraints 7 to 9 are time window constraints.

3 Insertion Heuristic Algorithm

The purpose of insertion heuristic algorithm is to insert some unvisited customers into the current routes to form feasible solutions. The algorithm inserts each customer into the current routing and scores it, and inserts the customer with the highest score into the corresponding location to form a new routing until all customers are inserted.

3.1 The Cost Value of Insertion Customers

Let r be the current partial solution and \( \bar{n}\) is the number of customer in it. U denotes the set of not visited customers. g(u, r, p) is the time when the vehicle arrives at u, where \(u\in U \) denote an insert customer and p is a insertion position of r. If r still satisfies the time window constraint after u insertion, then the insertion point p is called a feasible insertion position for u. Set \(\varPhi (u,r)\) as a set of feasible insertion positions when customer u is inserted into route r. Then we can calculate the cost value of each feasible insertion position for each insertion customer as formula 10.

$$\begin{aligned} \xi \left( {u,r} \right)&= \mathop {\min }\limits _{p \in \varPhi \left( {u,r} \right) } \{ \left( {{d_{{i_p}u}} + {d_{u{i_{p + 1}}}} - {d_{{i_p}{i_{p + 1}}}}} \right) \nonumber \\&~~~+ \frac{{\bar{n}}}{n}Chg\_V\left( {u,r} \right) + \frac{{\bar{n}}}{n}\max \left( {0,{a_u} - g\left( {u,r,p} \right) } \right) \} \end{aligned}$$
(10)

In formula 10, \(\xi (u,r)\) is the weighted sum of three elements: (i) Regardless of vehicle capacity limitation, the increment of routing distance when customer u is inserted; (ii) The additional cost denoted as \(Chg\_V(u,r) \) (see below) to be paid when the vehicle serving route r must be changed to the route which also visit customer u; (iii) The waiting time of the vehicle before the service customer u. The latter two terms are taken as coefficients by the ratio of \(\bar{n}\) to n in order to increase the weight of the two terms as the insertion heuristic algorithm proceeds. The first item has no weight coefficient because the distance relation of three points satisfies the triangular inequality.

To formally describe cost \(Chg\_V(u,r)\), let h be the type of vehicle serving route r and let \(h'\) be the cheapest type of vehicle we must use when u is added to the route. The cost is,

$$\begin{aligned} Chg\_V\left( {u,r} \right) = \left( {1 - \frac{{\bar{n}}}{n}} \right) {C_R} + \frac{{\bar{n}}}{n}{C_A} \end{aligned}$$
(11)

Where \(C_R\) is the relative fixed cost increase.

$$\begin{aligned} {C_R} = {F^{h'}}\sum \limits _{i \in r \cup \left\{ u \right\} } {\frac{{{q_i}}}{{{Q^{h'}}}}} - {F^h}\sum \limits _{i \in r} {\frac{{{q_i}}}{{{Q^h}}}} \end{aligned}$$
(12)

And \(C_A\) is the absolute fixed cost increase.

$$\begin{aligned} {C_A} = {F^{h'}} - {F^h} \end{aligned}$$
(13)

When calculating \(Chg\_V\), the ratio of \(\bar{n}\) to n is used to adjust the weight of \(C_R\) and \(C_A\). In most cases, the evaluation value of \(Chg\_V\) is mainly determined by \(C_A\), because insertion customers will increase the vehicle tolerance, so it is necessary to reselect the vehicle type. In a few cases, the insertion of customers will not change the vehicle type, and the \(Chg\_V\) is mainly determined by \(C_R\).

3.2 The Fitness Value of Inserted Customers

When the cost score of all insertion positions of each customer is obtained, then we use the fitness function to calculate the score of each customer, and select the next customer according to the fitness score and insert it into the corresponding position of the route. The fitness function can be shown as

$$\begin{aligned} \theta \left( u \right) = \left( {\mathrm{{s}}\min \xi \left( {u,r} \right) - \min \xi \left( {u,r} \right) } \right) + {\gamma _d}{d_{0u}} - {\gamma _w}\left( {{b_u} - {a_u}} \right) \end{aligned}$$
(14)

Where smin denotes the second minimum value; \(\gamma _d\) and \(\gamma _w\) are two weighing parameters, and this paper set \(\gamma _d=1.0\), \(\gamma _w=0.2\) according to Mauro [3]. \(\theta (u)\) consists of three parts: (i) the added cost value when the customer u is not assigned to its preferred route; (ii) the distance between u and the distribution center; (iii) the time window width of u.

3.3 The Process of Insertion Heuristic Algorithm

The insertion heuristic algorithm can be described as follows:

  • Step 1: Input: partial solution r; unvisited customer U; parameters;

  • Step 2: Choose an unvisited customer u from U;

  • Step 3: Compute the score \(\xi (u,r)\) [see 10] define r(u) and r(u) as the routes corresponding to the first and second minimum of \(\xi (u,r)\);

  • Step 4: Compute the score \(\theta (u)\) [see 14]; determine the customer \(\bar{u}\) with maximum \(\theta (u)\) value;

  • Step 5: If u can not form a feasible solution by inserting into the route, or the fixed cost of the fleet can be reduced if u is added to a new empty route, initialize a new route with customer \(\bar{u}\). Else insert \(\bar{u}\) into the position with the minimum \(\xi (u,r)\).

  • Step 6: Update the solution r and set \(U=U\backslash {\{u\}}\);

  • Step 7: Return to step 2 if U is not empty. Otherwise, the route r containing all the customers is output and the algorithm is terminated.

4 Hybrid Ant Colony Algorithm

In this paper, a hybrid ant colony algorithm is proposed. Firstly, the feasible solution is constructed using the same vehicle type (similar to VRPTW), and then the feasible solution is reconstructed using the insertion heuristic algorithm. The hybrid ant colony algorithm will be described in detail as follows.

4.1 The Preliminary Construction of Feasible Solutions

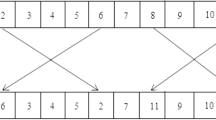
This paper uses the strategy of peripheral search to improve the search efficiency of ants in large-scale customers. Firstly, feasible customers are selected according to time window constraints and capacity constraints, and then several customers nearest to the current customers are selected as candidate customers set (\(\varOmega \)) from the set of feasible customers. As shown in the Fig. 1.

Fig. 1.
figure 1

Selection of candidate customers.

Full size image

Assuming that the current customer is i, the transition probability of ant from customer i to customer j can be expressed as

$$\begin{aligned} {p_{ij}} = \left\{ \begin{array}{l} \frac{{{S_{ij}} \times \tau _{ij}^\alpha \times \eta _{ij}^\beta }}{{\sum \limits _{j \in \varOmega } {{S_{ij}} \times \tau _{ij}^\alpha \times \eta _{ij}^\beta } }},j \in \varOmega \\ 0,otherwise \end{array} \right. \end{aligned}$$
(15)

Where \(p_{ij}\) is transition probability of ant from customer i to j; \(S_{ij}=d_{0i}+d_{0j}-d_{ij}\) is the saving value of i and j; \(\tau _{ij}\) is pheromone concentration between i and j; \(\eta _{ij}=\frac{1}{d_{ij}}\) is visibility of pheromone concentration; \(\alpha \), \(\beta \) are parameters.

The next customer j is chosen according to the following formula.

$$\begin{aligned} j = \left\{ \begin{array}{l} \arg \mathop {\max }\limits _{j \in \varOmega } \left( {{p_{ij}}} \right) ,~if~q > {p_t}\\ randomj \in \varOmega ,~otherwise \end{array} \right. \end{aligned}$$
(16)

Where q is a value chosen randomly with uniform probability in the interval [0,1]. \(p_t\) (\(0<p_t\le 1\)) interpreted as the definite selection probabilities is initiated as \(p_0= 1\) and is dynamically adjusted with the evolutionary process. The value of \(p_t\) is as follows

$$\begin{aligned} {p_t} = \left\{ \begin{array}{l} 0.95{p_{t - 1}},~if~0.95{p_{t - 1}} > {p_{\min }}\\ {p_{\min }},~otherwise \end{array} \right. \end{aligned}$$
(17)

Where \(p_{(min)}\) is the minimum defined in evolutionary process. It is used to ensure that certain selection opportunities can be obtained even if the value of \(p_t\) is too small. Formula 15 shows that in the early stage of iteration, j is selected randomly from the candidate customers according to the transition probability. With the iteration, j has a certain probability to be directly the customer with the largest transfer probability among the candidate customers. This selection strategy can accelerate the convergence of the algorithm and expand the search space at the same time.

When the feasible solution is preliminarily constructed by using ant colony algorithm, the vehicle capacity value is first set to the maximum type of capacity. Each ant starts from the distribution center and randomly chooses the next customer from the candidate customer set according to the state transition probability to construct a feasible routing. If there is no feasible customer added to the routing, the ant returns to the distribution center to complete the construction of a feasible routing. Then repeat the above process and continue to build a viable route from the remaining customers until all customers are accessed to complete the construction of a viable solution.

4.2 Decomposition Strategy of Feasible Solutions

Let \(R=\{R_1,R_2,...,R_m\}\) is a feasible solution constructed initially, where \(R_a\) \(\left( {1 \le a \le m}\right) \) is a feasible route. Since the solutions are all constructed according to the maximum vehicle load, they are not an appropriate solution for FSMVRPTW, so they need to be disassembled and reconstructed.

The purpose of the decomposition strategy is to decompose R into a routing set r containing partial customers and an unvisited customer set U. For each feasible route \(R_a \), firstly, the actual load of the current feasible route \(l_a\) is calculated. And then the customers exceeding the maximum vehicle capacity of less than \(l_a\) in \(R_a\) are removed. The remaining route is \(r_a\) which turn into a subset of r, and the removed customers are added to the set U. In particular, when \(l_a\) is smaller than the minimum vehicle type capacity, all customers in \(R_a\) will be removed and added to U.

4.3 The Process of Hybrid Ant Colony Optimization

The steps of the hybrid ant colony optimization algorithm for solving the FSMVRPTW model can be described as follows:

  • Step 1: Input the number of ant m, the maximum iteration number maxit and algorithmic parameters; initialize the current iteration number \(it = 1\);

  • Step 2: Initialize the ant number \(n = 1\);

  • Step 3: Preliminary construct a feasible solution of ant n using 4.1 algorithm, and the initial solution \(R^n\) is obtained.

  • Step 4: \(R^n\) is decomposed into \(r^n\) and \(U^n\) according to 4.2 algorithm. Where \(r^n\) is a partial solution of ant n and \(U^n\) is insert customer of ant n.

  • Step 5: The insertion heuristic algorithm in part 3 is used to insert the customers in \(U^n\) into \(r^n\). After the reconstructed solution is obtained, the cost \({ n}\) of the solution is calculated according to formula 1.

  • Step 6: \(n=n+1\). If \(n > m\), that is all ants have completed the solution construction, turn to step 7. Otherwise, return to step 2.

  • Step 7: Update the global pheromone as follows

    $$\begin{aligned} \tau _{ij}^{new} = \left( {1 - \rho } \right) *\tau _{ij}^{old} + \varDelta {\tau _{ij}} \end{aligned}$$
    (18)
    $$\begin{aligned} \varDelta {\tau _{ij}} = \left\{ \begin{array}{l} \sum \limits _{n = 1}^m {\frac{Q}{{\cos t\left( n \right) }}} ,~if~arc\left( {i,j} \right) \in {r^n}\\ 0,~otherwise \end{array} \right. \end{aligned}$$
    (19)

    Where \(\rho \left( {\mathrm{{0< }}\rho \mathrm{{ < 1}}} \right) \) is a constant representing the volatilization rate of pherom-ones; \(\varDelta {\tau _{ij}}\) is pheromone accumulation between customer i and j; Q is a constant, indicating the total amount of pheromones released by each ant. Because the pheromone superposition in ant colony optimization algorithm is a positive feedback process, in order to avoid stagnation of search, the maximum and minimum ant colony algorithm is adopted to limit the concentration of pheromone to \(\left[ {{\tau _{\min }},{\tau _{\max }}} \right] \), as shown in formula 20.

    $$\begin{aligned} {\tau _{ij}} = \left\{ \begin{array}{l} {\tau _{\max }},~if{\tau _{ij}} > {\tau _{\max }}\\ {\tau _{\min }},~if{\tau _{ij}} < {\tau _{\min }} \end{array} \right. \end{aligned}$$
    (20)

  • Step 8: \(it=it+1\). If it is bigger than maxit, then the flow of the algorithm finishes. Otherwise, go back to Step 2, and repeat the steps.

5 Numerical Analysis

Solomon benchmark problems  [14] is often used in the experiment of VRPTW algorithm. It has 56 problems in 6 categories: R1, R2, C1, C2, RC1 and RC2, each of which contains 100 customers. These 6 categories of problems can be divided into random distribution (R), cluster distribution (C) and mixed distribution (RC) according to customer distribution. The time windows of customer in R1, C1 and RC1 problems are narrower, while those in R2, C2 and RC2 problems are wider. For each instance of Solomon, Liu and Shen [2] introduced three different subclasses of instances, which are characterized by type a, type b and type c three different vehicle costs. In which type a vehicle costs are high, type b vehicle costs are medium, and type c vehicle costs are low. Combining each VRPTW instance with the cost of three types of vehicles, a total of 168 examples are obtained.

Table 1. Comparison of ACO and HACO in solving benchmark problems.
Full size table
Table 2. Average and comparison of problem results.
Full size table

In this paper, hybrid ant colony optimization algorithm (HACO), ant colony optimization algorithm (ACO) and tabu search (TS) are used to solve and compare the benchmark problems. The algorithm is programmed with MATLAB 2016a and runs on the personal computer of Intel Core i5-5200 CPU, 4G memory. The experimental parameters are as follows: the number of ants \(m=15\), the maximum number of iterations \( maxit = 50\), \( \rho =0.08\), \( \alpha =1.7\), \( \beta =2\) and \( Q=80\). One instances are selected from each type of benchmark problems and running five times to and calculating average value as the result. The experimental results of HACO, ACO and TS are shown in Table  1.

To illustrate the comparison of the results, we calculate the average values of various types of problems and average percentage error (label “\(\varDelta \%\)”). As shown in Table 2.

From Tables 1 and 2, we can see that all the results of HACO are better than ACO algorithm. The average value of HACO in type a is better than ACO 15.3%, better than TS 3.6%, in type b is better than ACO 18.7%, better than TS 10.5% and in type c is better than ACO 25.9%, better than TS 19.8%, which shows that the proposed HACO is feasible and improves the quality of solving multi-vehicle problem.

Figure 2 shows the convergence of ACO, HACO and TS in solving C101b. Both results are run five times and averaged for each generation.

Fig. 2.
figure 2

The convergence of ACO, HACO and TS in solving C101b

Full size image

From Fig. 2, we can see that with the progress of iteration, HACO converges faster and costs less, which shows that the hybrid algorithm proposed in this paper effectively improves the convergence speed of traditional ant colony optimization algorithm. The above results also show that the hybrid strategy proposed in this paper has the advantages of fast convergence and high solution quality. HACO effectively improves the ability of ant colony optimization algorithm to solve heterogeneous fleet problems, and provides a new idea for using ant colony algorithm to solve FSMVRPTW.

6 Conclusion

FSMVRPTW is closely related to real life. Because it is difficult to obtain exact solutions, a hybrid optimization algorithm combining ant colony algorithm and insertion heuristic algorithm is proposed in this paper. Firstly, a feasible solution is constructed by using a single type of vehicle, and then a new solution is generated by reconstructing the feasible solution through decomposition strategy and insertion strategy. Ant colony system has the advantages of strong global search ability and robustness in solving routing problems. The insertion heuristic algorithm solves the problem that ants can not select the appropriate vehicle type before constructing feasible routing. Hybrid ant colony optimization algorithm combines the advantages of ant colony algorithm and insertion heuristic algorithm, expands the application scope of ant colony algorithm, and provides a new way to solve FSMVRPTW.