Keywords

1 Introduction

Metro is the most effective way for passenger evacuation at intercity railway stations because of the superiorities of massive capacity, high speed and great reliability. In daily operation, most metro lines adopt peak/off-peak-based timetables. However, for metro lines connecting with intercity railway stations, whose inbound passenger flow varies significantly over a short period due to the discrete arrivals of intercity trains, regular timetables might increase waiting time of passengers [1]. Therefore, it is necessary to optimize timetable of such metro lines according to the time-varying passenger demand at the connecting station.

In the domain of demand-oriented metro timetable optimization, Berrena [2, 3] proposed timetable optimization model under dynamic passenger demand, Niu [4,5,6] analysed waiting behaviours of passengers at stations and constructed timetable optimization model with the aim of minimizing passenger waiting time. While above studies did not take transfer behaviours of passengers into account, Wu [7] put forward a model to minimize total waiting time of passengers including transfer passengers in a metro network. It only considered passengers transferring between different metro lines, however. Besides, passenger demands considered in above researches were all obtained through analysing historic data because passenger demands are similar in working days. For metro lines connecting with intercity railway stations, a slight change in arrival times of intercity trains can have a significant impact on passenger demand at the connecting station. Therefore, historic data of connecting stations is not universal and a passenger demand forecast model based on arrival times of intercity trains is called for.

Hu [8] built a train departure time optimization model for a metro line whose start station is connected to an intercity railway station, on the basis of characterizing the time-varying demand of passengers transferring from intercity trains to metros. Whereas the model proposed by Hu for the predication of the transfer passenger demand did not take the influence of the transfer facility layout into account. Also, the developed timetable model is only practical for single-direction metro lines where the start station is the connecting station and the capacity of metro trains can be neglected. It is not adaptable enough for a metro line where an intermediate station is connected to an intercity railway station.

To solve this problem, this paper puts forward a model to predict the number of passengers arriving at the platform of connection stations via analysing the entire process for passengers transferring from intercity trains to metros. Furthermore, a timetable optimization model aiming at minimizing passenger waiting time of a metro line where an intermediate station is connected to an intercity railway station is proposed. At last, a genetic algorithm is developed to find the optimal solution of the proposed model.

2 Model on Transfer Passenger Demand Predication

The entire process for passengers transferring from intercity trains to metros is shown in Fig. 1. According to arrivals of intercity trains and the transfer process of passengers, a model for calculating the number of passengers taking escalators and stairs, which are located at platforms of an intercity railway station, is proposed firstly, and the calculation result is regarded as the passenger flow input. Then, take the impact of each transfer facility (i.e. escalators/stairs, exit gates, etc.) into account and adjust the input passenger flow distribution orderly until the number of passengers arriving at the connecting station platform is obtained.

Fig. 1
figure 1

Process for passengers transferring from intercity trains to metros

Full size image

Transfer facilities considered of the transfer process are divided into two types: node facilities and facilities with branches. Facilities with branches are where two parallel facilities are provided for passengers to pass the same area, including escalators/stairs in addition to buying tickets at the station/using smart cards. Node facilities are those with capacity constraints, like exit gates of intercity railway stations and security checkpoints of metro stations. It is worth noting that escalators/stairs are also node facilities where passengers are influenced by capacity constraints after making choice between escalators and stairs.

2.1 Passenger Flow Input

It is very likely that more than one train get to the intercity railway station during the study period [0, T]. Therefore, the number of input passengers is calculated by the sum of passenger distribution of multiple trains:

$$C\left( t \right) = \mathop \sum \limits_{k = 1}^{K} A_{k} \left( t \right)$$
(1)

where \(C\left( t \right)\) is the total number of input passengers at time \(t\); \(A_{k} \left( t \right)\) is the number of input passengers for train \(k\) at time \(t\); \(K\) is the total number of intercity trains getting to the station during study period [0, T].

In general, transfer passengers spend different time walking from intercity trains to escalators/stairs which are located at platforms of an intercity railway station. According to Henderson’s research that walking speed of passengers follows normal distribution whose mean is \(\mu\), standard deviation is \(\sigma\) [9]. With the distribution of passenger walking speed and walking distance of passengers, the distribution of passenger walking time can be calculated. Substitute the capacity of intercity trains, the number of input passengers for train \(k\) at time \(k\) is calculated by:

$$A_{k} \left( t \right) = Q_{k} H\left( {\mu ,\delta ,t,l_{k} } \right)$$
(2)
$$Q_{k} = P_{k} \times \varepsilon$$
(3)

where \(Q_{k}\) is number of transfer passengers from train \(k\) reaching the intercity railway platform; \(H\) is the distribution of passenger walking time; \(l_{k}\) is the average distance for passengers walking from train \(k\) to escalators/stairs on the intercity railway platform; \(P_{k}\) is the capacity of train \(k\); \(\varepsilon\) is the load factor of intercity trains.

2.2 Facilities with Branches

Facilities with branches are where passengers need to make choice according to their conditions. For example, they need to decide whether to take escalators or stairs, whether to buy tickets at the station or use smart cards directly. Investigations on passengers using facilities with branches infer that it takes passengers nearly the same time to go through escalators and stairs, while the time they spent on buying tickets at the station is longer than using smart cards. As a result, the number of passengers choosing escalators and stairs is calculated, respectively, by:

$$L^{1} \left( t \right) = aL^{0} \left( t \right)$$
(4)
$$L^{2} \left( t \right) = \left( {1 - \alpha } \right)L^{0} \left( t \right)$$
(5)

where \(L^{1} \left( t \right)\) is the number of passengers choosing stairs at time \(t\); \(L^{2} \left( t \right)\) is the number of passengers choosing escalators at time \(t\); \(L^{0} \left( t \right)\) is the number of passengers who intend to take escalators/stairs; \(\alpha\) is the proportion of passengers who choose stairs.

The number of passengers passing AFC is calculated by:

$$S\left( t \right) = bS^{0} \left( t \right) + \left( {1 - b} \right)S^{0} \left( {t - t_{0} } \right)$$
(6)

where \(S\left( t \right)\) is the number of passengers going through AFC at time \(t\); \(S^{0} \left( t \right)\) is the number of passengers intend to use AFC machines; \(b\) is the proportion of passengers passing AFC machines directly with smart cards; \(t_{0}\) is the service lag time for passengers buying tickets at the station instead of using smart cards.

2.3 Node Facilities

Generally speaking, passengers who intend to take escalators will move to stairs when the entry of escalators is too crowded. Therefore, considering the capacity constraints of escalators/stairs, the number of passengers choosing stairs and escalators is re-calculated, respectively, by:

$$L^{1} \left( t \right) = L^{1} \left( t \right) + { {\max} }\left\{ {0,\eta \left( {L^{2} \left( t \right) - c_{2} } \right)} \right\}$$
(7)
$$L^{2} \left( t \right) = L^{2} \left( t \right) - { {\max} }\left\{ {0,\left( {1 - \eta } \right)\left( {L^{2} \left( t \right) - c_{2} } \right)} \right\}$$
(8)

where \(\eta\) is the number of passengers who change their choice and decide to take stairs rather than escalators; \(c_{2}\) is service capacity of escalators.

Based on the re-calculated \(L^{1} \left( t \right)\) and \(L^{2} \left( t \right)\), the number of passengers going through stairs and escalators is expressed by:

$$L^{3} \left( {t + 1} \right) = {\min} \left\{ {L^{1} \left( {t + 1} \right) + {\max} \left\{ {0, L^{1} \left( t \right) - c_{1} } \right\},c_{1} } \right\}$$
(9)
$$L^{4} \left( {t + 1} \right) = {\min} \left\{ {L^{2} \left( {t + 1} \right) + {\max} \left\{ {0, L^{2} \left( t \right) - c_{2} } \right\}, c_{2} } \right\}$$
(10)

where \(L^{3} \left( t \right)\) is the number of passengers going through stairs at time \(t\); \(L^{4} \left( t \right)\) is the number of passengers going through escalators at time \(t\); \(c_{1}\) is the capacity of stairs; \(c_{2}\) is the capacity of escalators.

Exit gates and security checkpoints have similar effect on the distribution of passenger flow, which is expressed, respectively, by:

$$J^{1} \left( {t + 1} \right) = {\min} \left\{ {J^{0} \left( {t + 1} \right) + {\max} \left\{ {0,J^{0} \left( t \right) - c_{3} } \right\},c_{3} } \right\}$$
(11)
$$G^{1} \left( {t + 1} \right) = {\min} \left\{ {G^{0} \left( {t + 1} \right) + {\max} \left\{ {0,G^{0} \left( t \right) - c_{4} } \right\},c_{4} } \right\}$$
(12)

where \(J^{1} \left( t \right)\) is the number of passengers passing security checkpoints at time \(t\); \(G^{1} \left( t \right)\) is the number of passengers getting through exit gates at time \(t\); \(J^{0} \left( t \right)\) and \(G^{2} \left( t \right)\) are the number of passengers who intend to be through security checkpoints and exit gates, respectively.

3 Timetable Optimization Model and Solution Methodologies

As shown in Fig. 2, this paper considers a bi-direction metro line with N stations which have been numbered sequentially from the up direction to the down direction. Although station 1 and station \(2N\), station 2 and station \(2N - 1\), …, station \(N + 1\) and station \(N\) refer to the same station in terms of geographic location, they are numbered separately to make the timetable model more understandable. Station \(n\), that is station \(2N - n + 1\), is the metro station which connects to an intercity railway station.

Fig. 2
figure 2

Representation of a metro line

Full size image

3.1 Objective Function

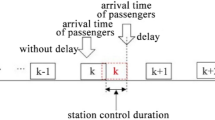
Divide the study period [0, T] into a host of time intervals denoted by \(t\) (\(t = 1,2,3,4, \ldots\)). Assume that all passengers arrive at metro stations at the end of each time interval, and all metro trains start their operation from the terminal station where the depot is located and turn around at the other terminal station. In order to evacuate passengers that get to the platform of connecting stations, this paper takes minimizing passenger waiting time at connecting stations as the objective of the timetable optimization model and it is calculated by:

$${\min} W = W_{1} + W_{2}$$
(13)
$$W_{1} = \mathop \sum \limits_{j = 1}^{K} \mathop \sum \limits_{v = n + 1}^{2N} \mathop \sum \limits_{{t \in \left( {L_{j - 1}^{n} ,L_{j}^{n} } \right]}} P^{n,v} \left( t \right)\left( {TD_{j}^{n} - t} \right)$$
(14)
$$W_{2} = \mathop \sum \limits_{j = 1}^{K} \mathop \sum \limits_{v = 2N - n + 2}^{2N} \mathop \sum \limits_{{t \in \left( {L_{j - 1}^{2N - n + 1} , L_{j}^{2N - n + 1} } \right]}} P^{2N - n + 1} \left( t \right)\left( {TD_{j}^{2N - n + 1} - t} \right)$$
(15)

where \(W_{1}\) is the waiting time of passengers at the connecting station when travelling towards up direction; \(W_{2}\) is the waiting time of passengers at the connecting station when travelling towards down direction; \(P^{n,v} \left( t \right)\) is the number of passengers travelling from connecting station \(n\) to station \(v\); \(TD_{j}^{n}\) is the time when train \(j\) departs from station \(n\); \(K\) is the total number of trains departing from the start terminal during the study period; \(L_{j}^{n}\) is the effective loading time of train \(j\) at station \(n\).

Based on train departure times at the first station, running times at sections and dwell times at stations, train departure times at the connection station on up direction and down direction are expressed by:

$$TD_{j}^{n} = TD_{j}^{1} + \mathop \sum \limits_{u = 1}^{n} d_{j}^{u} + \mathop \sum \limits_{u = 1}^{n - 1} r_{j}^{u}$$
(16)
$$TD_{j}^{2N - n + 1} = TD_{j}^{1} + \mathop \sum \limits_{u = 1}^{2N - n + 1} d_{j}^{u} + \mathop \sum \limits_{u = 1}^{2N - n} r_{j}^{u}$$
(17)

where \(d_{j}^{u}\) is the dwell time of train \(j\) at station \(u\); \(r_{j}^{u}\) is the running time of train \(j\) from station \(u\) to station \(u + 1\).

3.2 Constraints

Whether a passenger can get on the oncoming train successfully depends on the remaining loading capacity of the train. In order to determine the number of passengers who can board the train, effective loading time is introduced, that is the critical time that the number of passengers onboard reaches the maximum loading capacity. The effective loading time for train \(j\) is at station \(u\) is calculated by:

$$L_{j}^{u} = { {\min} }\left\{ {TD_{j}^{u} ,{\max} \left\{ {\tau | \mathop \sum \limits_{{t \in \left( {L_{j - 1, \tau }^{u} } \right]}} \mathop \sum \limits_{v = u + 1}^{2N} P^{u,v} \left( t \right) \le C - R_{j}^{u - 1} + \mathop \sum \limits_{{u^{\prime} = 1}}^{u - 1} B_{j}^{{u^{\prime},u}} } \right\}} \right\}$$
(18)
$$B_{j}^{u,v} = \mathop \sum \limits_{{t \in \left( {L_{j - 1}^{u} , L_{j}^{u} } \right]}} P^{u,v} \left( t \right)$$
(19)
$$Q_{j}^{u} = R_{j}^{u - 1} - \mathop \sum \limits_{{u^{\prime}}}^{u - 1} B_{j}^{{u^{\prime}, u}}$$
(20)
$$R_{j}^{u} = Q_{j}^{u} + \mathop \sum \limits_{v = u + 1}^{2N} B_{j}^{u, v}$$
(21)

where \(B_{j}^{u,v}\) is the number of passengers travelling from station \(u\) to \(v\) who board train \(j\) successfully; \(Q_{j}^{u}\) is the number of passengers left on train \(j\) after some passengers get off at station \(u\); \(R_{j}^{u}\) is the number of onboard passengers after train \(j\) departs from station \(u\); \(C\) is maximum loading capacity of metro trains.

To cover all passenger demand over the study period [0, T], departure times of the first train and the last train are pre-determined, which are denoted by:

$$TD_{0}^{1} = 0$$
(22)
$$TD_{K + 1}^{1} = T$$
(23)

Constraints of the headway between two adjacent trains are calculated by:

$$h_{{\min} } \le TD_{j}^{1} - TD_{j - 1}^{1} \le h_{{\max} }$$
(24)

where \(h_{\min}\) is the minimum headway; \(h_{\max}\) is the maximum headway.

3.3 Solution Methodologies

The proposed timetable optimization model has a large solution space. In order to improve the efficiency of problem-solving, a genetic algorithm is adopted, the framework of which is shown in Fig. 3. In this study, chromosomes are binary coded, and the length of each chromosome depends on how many time intervals the study period is divided into. Each gene represents an alternative departure time of a train at the first station. If it equals “1”, it means that a train departs at this time interval and “0” means no trains depart.

Fig. 3
figure 3

Flowchart of the adopted generic algorithm

Full size image

4 Case Studies

The developed transfer passenger demand predication model and timetable optimization model are applied to Beijing Metro Line 9 where an intermediate station called Beijing West Metro Station connects to Beijing West Railway Station. The study period is 12:30–14:00 on a working day when intercity trains get to Beijing West Railway Station intensively.

4.1 Passenger Demand Predication of the Connecting Station

Based on investigations on the entire process for passengers transferring from intercity trains of Beijing West Railway Station to Beijing Metro Line 9, parameters of the passenger demand predication model are obtained, which are shown in Table 1.

Table 1 Parameters of the passenger demand predication model
Full size table

As Beijing Metro Line 9 and Beijing Metro Line 7 are both connected with Beijing West Railway Station, this paper assumes that half of the passengers who intend to transfer from intercity trains to metros take Beijing Metro Line 9. Based on arrival times of intercity trains at Beijing West Railway Station over the study period and above parameters, the result of passenger demand predication is shown in Fig. 4.

Fig. 4
figure 4

Calculated passenger demand at Beijing West Metro Station

Full size image

4.2 Accuracy of Passenger Demand Predication

Compare the accuracy of passenger demand predication in this paper to that calculated by Hu in 2016 under different time intervals. As Table 2 shows, the predication model proposed in this paper has a smaller error and this advantage becomes more significant as the time interval becomes shorter.

Table 2 Accuracy comparison of passenger demand predication models
Full size table

4.3 Timetable Optimization of Beijing Metro Line 9

Input the results of passenger demand predication at the connecting station to the timetable optimization model and use GA to find the solutions. As the selected time interval is 10 s and the length of the study period is 90 min, the length of each chromosome is 540. Other parameters of GA are shown in Table 3.

Table 3 Parameters of GA adopted in the case study
Full size table

Table 4 represents passenger waiting time of current timetable and the optimized timetable. It is found that the optimized timetable reduces passenger waiting time at the connecting station by 23.57%. Although the passenger waiting time at other stations increases by 1.61%, it is too low to affect riding experience of passengers. It is also noted that saving rate of passenger waiting time is higher when train capacity is neglected. However, the maximum load factor reaches 136.86% under this condition. If train capacity is considered, the maximum load factor is only 98.86%. As a result, the congestion on metro trains is relieved and service quality for passengers is improved.

Table 4 Passenger waiting time of current timetable and the optimized timetable
Full size table

5 Conclusions

Based on the analysis on the entire process for passengers transferring from intercity trains to metro trains, a mathematical model is proposed to predict the number of passengers getting to the platform of a metro station which connects with an intercity railway station. Compared to the existing research, the passenger demand predication model developed in this paper is more accurate.

According to the calculated passenger demand, a timetable optimization model with the aim of minimizing passenger waiting time at a connecting station is established and solved by GA. Real-world case studies indicate that the optimized timetable can reduce passenger waiting time at the connecting station by 23.57% with negligible influence on passengers at other stations.

The timetable optimization model proposed in this paper takes train capacity into account, which improves service quality for passengers to some extent. However, this paper only considers the case that a metro line connects with an intercity railway station. However, some intercity railway stations connect with several metro lines. How to optimize their timetables coordinately will be introduced in the further work.