Keywords

Introduction

Although Rasch modeling (Rasch, 1980) is a powerful psychometric tool, for novices its functionality is a “black box.” In reaction most quantitative researchers favor classical test theory (CTT) for its conceptual clarity and procedural simplicity (Hutchinson & Lovell, 2004). One problem involved with using Rasch modeling is that it is often confused with item response theory (IRT), and as a result users cannot decide what assessment approach is suitable for their data. To rectify the situation, this non-technical introduction starts with an explanation of how Rasch modeling can remediate the shortcomings of CTT. Next, theoretical assumptions and major procedural components of Rasch modeling are illustrated with concrete examples. Further, Rasch modeling can be applied using both dichotomous and polytomous data; hence, different modeling methods, including the partial credit model and the graded response model, are introduced. Because comparison of Rasch modeling and IRT requires the preceding information, their differences are discussed at the end. Finally, the merits and shortcomings of two powerful software applications for Rasch analysis—namely, SAS (SAS Institute, 2018) and Winsteps (Winsteps & Rasch measurement Software, 2019)—are discussed.

Classical Test Theory Versus Rasch Modeling

The root of classical test theory (CTT), also known as the true score model (TSM), could be traced back to Spearman (1904). Conceptually and procedurally speaking CTT is very straight-forward. According to this approach, item difficulty and person ability are conceptualized as relative frequencies. For instance, if a student is able to correctly answer 9 out of 10 questions in a test, according to the total score his or her ability would be quantified as 9/10 = 0.9 or 90%. The item attribute can also be computed by percentage. For example, if only 2 out of 10 students can correctly answer a particular item in a test, obviously this question would be considered very challenging: 2/10 = 0.2 or 20%. However, this approach of assessing student ability is item-dependent. If the test is composed of easy items, even an average student might look very competent. In a similar vein, the CTT approach of evaluating the psychometric properties of test items is sample-dependent. If the students are very good at the subject matter in the test, then even challenging items might seem easy. This issue is called circular dependency. Rasch modeling, which estimates item difficulty and person ability simultaneously, is capable of overcoming this circular dependency. Because comparison of person ability is unaffected by the choice of items and comparison of items is also unbiased by the choice of participants, Rasch modeling is said to be a form of objective measurement that can yield invariant measurement properties across various settings (Wright, 1992). Details regarding the estimation are discussed in the section on item calibration and ability estimation.

In addition, CTT is built upon the philosophy of true score model (TSM). True score model is so named because its equation is expressed as: X = T + E, where:

  • X = fallible, observed score

  • T = true score

  • E = random error

Ideally, a true score reflects the exact value of a respondent’s ability or attitude. The theory assumes that traits are constant and the variation in observed scores are caused by random errors, which result from numerous factors, such as guessing and fatigue. These random errors over many repeated measurements are expected to cancel each other out (e.g. sometime the tester is so lucky that his or her observed scores are higher than his or her true scores, but sometimes he or she is unlucky and his or her observed scores are lower). In the long run, the expected mean of measurement errors should be zero. When the error term is zero, the observed score is the true score: X = T + 0 → X = T.

On the other hand, some modern Rasch modelers do not assume that there exists a true score for each person. Rather, they subscribe to the notion that uncertainty is an inherent property of any estimation, and that there might thus be a score distribution within the same person. For example, in large-scale international assessments, such as the Programme for International Student Assessment (PISA) and the Programme for International Assessment of Adult Competencies (PIAAC), for every participant there are ten plausible scores, known as plausible values (PV) (OECD, 2013a, 2013b). These plausible values represent the estimated distribution for a student’s θ (student ability). In psychometrics, this distribution is known as the posterior distribution (Wu, 2004, 2005).

Assumptions of Rasch Modeling

Unidimensionality

One of the foundational assumptions of Rasch modeling is unidimensionality, meaning that all items in the scale are supposed to measure a single construct or concept. A typical example is that a well-written math test should evaluate the construct of mathematical capability. This approach can come with limitations. For example, if a test designer uses a long passage to illustrate a math problem, this item may end up simultaneously challenging both math and comprehension abilities, thereby becoming multidimensional rather than unidimensional. This is problematic because it complicates the interpretability of results; to explain, if a student receives a low score on a test, it will be difficult to determine whether this score is due to deficits in this student’s mathematical or reading ability.

Some psychometricians argue that many assessment tests are multidimensional in nature. Returning to the example of a math test—this type of test might include questions about algebra, geometry, trigonometry, statistics, and calculus. By the same token, a science test may include questions about physics, chemistry, and biology. Bond and Fox (2015) noted that psychometricians must choose the level of aggregation that can form a coherent and unidimensional latent construct. While it may be reasonable to lump algebra, geometry, trigonometry, statistics, and calculus into a construct of mathematical reasoning, and to lump physics, chemistry, and biology into the construct of scientific logic, it can be problematic to lump GRE-verbal, GRE-quantitative, and GRE-analytical together into a single construct.

Local Independence

Another major assumption of Rasch modeling is conditional independence, also known as local independence. It is assumed that there is no relationship between items that is not accounted for by the Rasch model. In CTT, psychometricians usually employ factor analysis to explore and confirm construct validity. In the context of Rasch modeling, Borsboom and Markus (2013) used the following analogy to illustrate the notion of construct validity in measurement: Variations in the construct must cause variations in the scores yielded by the instrument. For instance, changes in the temperature should cause the rise or fall of the mercury level in a thermometer. Conditional independence specifies that after the shared variance among the observed items has been captured, the unique variance (i.e. the residuals or random errors) should be independent. In this case, there should be a covariation between the latent trait and the observed items. Simply put, the latent construct causes variation in the item scores. This is how construct validity can be established, using a valid Rasch model (Baghaei, Shoahosseini, & Branch, 2019).

One may argue that in CTT the same mechanism can be provided by item-total correlation, such as point-biserial correlation. Baghaei et al. (2019) argued against this classical approach by pointing out that while Rasch modeling estimates the latent ability score, also known as the theta, there is no such thing in CTT (The concept of theta will be explained in the next section). In item-total correlation the total score is nothing more than a summation of item scores; there is no advanced algorithm to take item difficulty and person ability into account. At most the total score can represent content validity only.

Item Calibration and Ability Estimation

Unlike CTT, in which test scores of the same examinees may vary from test to test (depending upon test difficulty), in IRT item parameter calibration is sample-free, while examinee proficiency estimation is item-independent. In a typical process of item parameter calibration and examinee proficiency estimation, the data are conceptualized as a two-dimensional matrix, as shown in Table 4.1.

Table 4.1 5 × 5 person by item matrix
Full size table

In this example, Person 1, who answered all five items correctly, is tentatively considered as having achieved 100% proficiency, Person 2 is treated as having achieved 80% proficiency, Person 3 is treated as having achieved 60%, etc. These percentages are considered tentative because: (1) in Rasch analysis there is a specific set of terminology and scaling scheme for proficiency, and (2) a person’s ability cannot be based solely on the number of correct items he or she obtained, as item attributes should also be taken into account. In this highly simplified example, no examinees have the same raw scores. But what would happen if there was an examinee (e.g. Person 6) whose raw score was the same as that of another examinee (e.g. Person 4)? (see Table 4.2).

Table 4.2 Example of two people with the same raw score
Full size table

We cannot draw a firm conclusion that these two people have the same level of proficiency because Person 4 answered two easy items correctly, whereas Person 6 answered two hard questions instead. Nonetheless, for the simplicity of this illustration, we will stay with the five-person example. This neat five-person example illustrates an ideal case in which proficient examinees succeed on all items, less competent examinees succeed on the easier items and fail on the hard ones, and poor students fail on all items (see Table 4.1). This ideal case is known as the Guttman pattern (Guttman, 1944), but it rarely happens in reality. If it happened, the result would be considered an overfit. In non-technical terminology, this result would simply be “too good to be true.”

We can also make a tentative assessment of the item attribute based on this ideal-case matrix. Let’s look back at Table 4.1. Item 1 seems to be the most difficult because only one person out of five could answer it correctly. It is tentatively asserted that the difficulty level in terms of the failure rate for Item 1 is 0.8, meaning that 80% of students were unable to answer the item correctly. In other words, the item is so difficult that it can “beat” 80% of students. The difficulty level for Item 2 is 60%, Item 3 is 40% … etc. Please note that for person proficiency we count the number of successful answers, but for item difficulty we count the number of failures. While this matrix is nice and clean, the issue would be very complicated when some items have the same pass rate but are passed by examinees of different levels of proficiency.

In Table 4.3, Item 1 and Item 6 have the same level of difficulty. However, Item 1 was answered correctly by a person with high proficiency (83%) whereas Item 6 was not (the person who answered it had 33% proficiency). If the text in Item 6 confuses good students, then the item attribute of Item 6 would not be clear-cut. For convenience of illustration, we call the portion of correct answers for each person “tentative student proficiency” (TSP) and the pass rate for each item “tentative item difficulty” (TID). Please do not confuse these “tentative” numbers with the item difficulty parameter and the person theta in the final Rasch model.

Table 4.3 Two items share the same pass rate
Full size table

In short, when conducting item calibration and proficiency estimation, both item attribute and examinee proficiency should be taken into consideration. This is an iterative process in the sense that tentative proficiency and difficulty derived from the data are used to fit the model, and the model is employed to predict the data. Needless to say, there will be some discrepancy between the model and the data in the initial steps. It takes many cycles to reach convergence.

Given the preceding tentative information, we can predict the probability of answering a particular item correctly given the proficiency level of an examinee using the following equation:

$${\text{Probability}} = { \exp }\left( {{\text{proficiency }}{-}{\text{ difficulty}}} \right)/( 1+ { \exp }\left( { - \left( {{\text{proficiency }}{-}{\text{ difficulty}}} \right)} \right))$$

where

Exp is the Exponential Function; e = 2.71828.

By applying the above equation, we can give a probabilistic estimation about how likely a particular person is to answer a specific item correctly. As mentioned before, the data and the model do not necessarily fit together. This residual information can help a computer program to further calibrate the estimation until the data and the model converge. In this sense, parameter estimation in Rasch modeling is a form of residual analysis.

Information Provided by Rasch Modeling

Item Characteristic Curve (ICC)

From this point on, we give proficiency a special name: Theta, which is usually denoted by the Greek symbol θ. Rasch modeling is characterized by its simplicity, meaning that only one parameter is needed to construct the ICC. This parameter is called the B parameter, also known as the difficulty parameter or the threshold parameter. This value tells us how easy or how difficult an item is and can be utilized to model the response pattern of a particular item, using the following equation:

$${\text{Probability }} = { \exp }\left( {{\text{proficiency }}{-}{\text{ difficulty}}} \right)/( 1+ { \exp }( - ({\text{theta}}{-}{\text{ difficulty}})))$$

After the probabilities of giving the correct answer across different levels of θ are obtained, the relationship between the probabilities and θ can be presented as an Item Characteristic Curve (ICC), as shown in Fig. 4.1.

Fig. 4.1
figure 1

Item characteristic curve (ICC) of an average item

Full size image

In Fig. 4.1, the x-axis is the theoretical θ (proficiency) level, ranging from −5 to +5. Please keep in mind that this graph represents theoretical modeling rather than empirical data. To be specific, there may not be examinees who are deficient or proficient enough to reach a level of −5 or +5. Nevertheless, in order to study the “performance” of an item, we are interested in knowing—for a person whose θ is +5, what the probability of giving a correct answer might be. Figure 4.1 shows a near-ideal case. The ICC indicates that when θ is zero (i.e. average), the probability of answering the item correctly is almost 0.5. When θ is −5, the probability is almost zero. When θ is +5, the probability increases to 0.99.

Figure 4.2 shows the ICC of a difficult item. When the skill level of a student is average, the probability of scoring this item correctly is as low as 0.1. If θ is −5, there is no chance of scoring this item correctly. Figure 4.3 depicts the opposite scenario, in which an average student (θ = 0) has a 95% chance of answering the question correctly, whereas an unprepared student (θ = −5) has a 10% chance.

Fig. 4.2
figure 2

Item characteristic curve (ICC) of a difficult item

Full size image
Fig. 4.3
figure 3

Item characteristic curve (ICC) of an easy item

Full size image

Item Information Function and Test Information Function

In Fig. 4.1, when the θ is 0 (average), the probability of obtaining the right answer is 0.5. When the θ is 5, the probability is 1; when the θ is −5, the probability is 0. The last two cases raise the problem of missing information. To illustrate—if ten competent students answered the item in this example correctly, it would be impossible to determine which student was more competent than the others, with respect to domain knowledge. Similarly, if ten incompetent students failed the item in this example, it would be impossible to determine which student was less competent than the others, with regard to the subject matter. In other words, we have virtually no information about the θ in relation to the item parameter at the extreme poles, and increasingly less information as the θ moves away from the center toward the two ends. Not surprisingly, if a student was to answer all items in a test correctly, his or her θ could not be estimated. Similarly, if an item was to be answered correctly by all candidates, the difficulty parameter for this item could not be estimated. To summarize, the same problem occurs when all students fail or pass the same item; in either case, the result is that the item parameter cannot be computed.

There is a mathematical way to compute how much information each ICC can yield. This method is called the Item Information Function (IIF). The meaning of “information” in this term, can be traced back to R. A. Fisher’s notion that information is defined as the reciprocal of the precision with which a parameter is estimated. If one can estimate a parameter with precision, one can know more about the value of the parameter than if one had estimated it with less precision. The precision is a function of the variability of the estimates around the parameter value—it is the reciprocal of the variance, and the formula is: Information = 1/(variance).

In a dichotomous situation, the variance is p(1 − p) where p = parameter value. Based on the item parameter values, one can compute and plot the IIFs for the items, as shown in Fig. 4.4.

Fig. 4.4
figure 4

Item information functions

Full size image

Obviously, these IIFs differ from each other. In Item 1 (the line with diamonds), the maximum amount of information can be obtained when the θ is −1. When the θ is −5, there is still some amount of information (0.08). But there is virtually no information when the θ is 5. In item 2 (the line with squares), the maximum amount of information is centered at θ = 0, while the amount of information in the lowest θ is the same as that in the highest θ. Item 3 (the line with triangles) is the opposite of Item 1. On this item one might have much information near the higher θ, but information would drop substantively as the θ approached the lower end.

The Test Information Function (TIF) is simply the sum of all IIFs in the test. While IIF can provide information on the precision of a particular item parameter, the TIF can provide this information at the exam level. When there is more than one form of the same exam, the TIF can be used to balance the forms. One of the purposes of using alternate test forms is to avoid cheating. For example, consider the written portion of the driver license test. Usually different test-takers receive different sets of questions and it is futile for a test-taker to peek at his/her neighbor. However, it is important to ensure that all alternate forms carry the same values of TIF across all levels of theta, as shown in Fig. 4.5.

Fig. 4.5
figure 5

Balancing form A to D using the Test information function (TIF)

Full size image

Logit and Item-Person Map

One of the beautiful features of the Rasch modeling is that item and examinee attributes can be presented on the same scale (i.e. the logit scale). Before explaining the logit, it is essential to explain odds. The odds for the item dimension is the ratio of the number of the non-desired events (Q) to the number of the desired events (P). The formula can be expressed as: Q/P. For example, if the pass rate of an item is four of out five candidates, the desired outcome of passing the item would be 4 counts, and the non-desired outcome would be failing the question (1 count). In this case, the odds would be 1:4 = 0.25.

The odds can also be conceptualized as the probability of non-desired outcomes, relative to the probability of a desired outcome. In the above example, the probability of answering the items correctly is 4/5, which is 0.8, and the probability of failing is 1−0.8 = 0.2. Thus, the odds is 0.2/0.8 = 0.25. In other words, the odds can be expressed as (1 − P)/P. The relationships between probabilities (p) and odds are expressed in the following equations:

  • Odds = P/(1 − P) = 0.20/(1–0.20) = 0.25

  • P = Odds/(1 + Odds) = 0.25/(1 + 0.25) = 0.20

The logit is the natural logarithmic scale of the odds, which is expressed as: Logit = Log(Odds).

In Rasch modeling we can list item and examinee attributes on the same scale. How can one compare apples and oranges? The trick is to convert the values from two measures into a common scale: the logit. One of the problems of scaling is that spacing in one portion of the scale is not necessarily comparable to spacing in another portion of the same scale. To be specific, the difference between two items in terms of difficulty near the midpoint of the test (e.g. 50% and 55%) does not equal the gap between two items at the top (e.g. 95% and 100%) or at the bottom (5% and 10%). Consider weight reduction as a metaphor: It is easier for me to reduce my weight from 150 to 125 lbs, but it is much more difficult to trim my weight from 125 to 100 lbs. However, people routinely misperceive that distances in raw scores are comparable. By the same token, spacing in one scale is not comparable to spacing in another scale. Rescaling by logit solves both problems. In short, log transformation can turn scores measured in an ordinal scale into interval-scaled scores (Wright & Stone, 1979). However, it is important to point out that while the concept of logit is applied to both person and item attributes, the computational method for person and item metrics are slightly different. For persons, the odds for persons is calculated as P/(1 − P) whereas for items it is (1 − P)/P. In the logit scale, the original spacing is compressed. As a result, equal intervals can be found on the logit scale, as shown in Table 4.4.

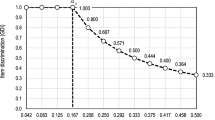
Table 4.4 Spacing in the original and the log scale
Full size table

The item difficulty parameter and the examinee theta are expressed in the logit scale, and their relationships are presented in the Item-Person Map (IPM), also known as the dual plot or Wright’s map, in which both types of information can be evaluated simultaneously. Figure 4.6 is a typical example of IPM. In Fig. 4.6, observations on the left hand side are examinee ability whereas those on the right hand side are item parameter values. This IPM can tell us the “big picture” of both items and students. The examinees on the upper right are said to be “better” or “smarter” than the items on the lower left, which means that those easier items are not difficult enough to challenge those highly proficient students. On the other hand, the items on the upper left outsmart examinees on the lower right, which implies that these tough items are beyond their ability level. In this example, the ability level of the highlighted students on the upper right is 1.986. It is no wonder that these students can “beat” all the items in this exam.

Fig. 4.6
figure 6

Item-person map

Full size image

Misfit

In Fig. 4.6, it is obvious that some students are situated at the far end of the distribution. In many statistical analyses we label them as “outliers.” In psychometrics there is a specific term for this type of outliers: Misfit. It is important to point out that the fitness between data and model during the calibration process is different from the misfit indices for item diagnosis. Many studies show that there is no relationship between item difficulty and item fitness (Dodeen, 2004; Reise, 1990). As the name implies, a misfit is an observation that cannot fit into the overall structure of the exam. Misfits can be caused by many reasons. For example, if a test developer attempts to create an exam pertaining to American history but accidentally includes an item about European history in this exam, then it is expected that the response pattern for the item on European history will differ substantially from that of the other items. In the context of classical test theory, this type of item is typically detected either by point-biserial correlation or by factor analysis. In Rasch modeling, this issue is identified by examining misfit indices.

Model Fit

SAS’s IRT outputs five global or model fit indices: the log likelihood, Akaike information criteria (AIC), Bayesian information criterion (BIC), likelihood ratio Chi-square G2 statistic, and Pearson’s Chi-square. AIC and BIC are useful when the analyst wants to compare across multiple tests or different sections of the same test in terms of model goodness. It is important to note that neither AIC nor BIC has an absolute cut-off. Rather, these values are used as relative indices in model comparison. The principle that underlies both AIC and BIC is in alignment with Ockham’s razor: Given the equality of all other conditions, the simplest model tends to be the best; and simplicity is a function of the number of adjustable parameters. Thus, a smaller AIC or BIC suggests a better model. However, Cole (2019) argued that when there are only a few items in the test, these overall model fit statistics are not suitable for test calibration.

Another way to check model fit is to utilize item fit information, meaning that all individual item fit statistics are taken into account as a whole. This can be accomplished by looking into infit and outfit statistics yielded by Winsteps. In a typical Winsteps output, “IN.ZSTD” and “OUT.ZSTD” stand for “infit standardized residuals” and “outfit standardized residuals.” To explain their meanings, regression analysis can be used as a metaphor. In regression a good model is expected to have random residuals. A residual is the discrepancy between the predicted position and the actual data point position. If the residuals form a normal distribution with the mean as zero, with approximately the same number of residuals above and below zero, we can tell that there is no systematic discrepancy. However if the distribution of residuals is skewed, it is likely that there is a systematic bias, and the regression model is invalid. While item parameter estimation, like regression, will not yield an exact match between the model and the data, the distribution of standardized residuals informs us about the goodness or badness of the model fit. The easiest way to examine the model fit is to plot the distributions, as shown Fig. 4.7.

Fig. 4.7
figure 7

Distributions of infit standardized residuals (left) and outfit standardized residuals (right)

Full size image

In this example, the fitness of the model is in question because both infit and outfit distributions are skewed. The darkened observations are identified as “misfits.” The rule of thumb for using standardized residuals is that a value >2 is considered bad. However, Lai, Cella, Chang, Bode, and Heinemann (2003) asserted that standardized residuals are still sample size dependent. When the sample size is large, even small and trivial differences between the expected and the observed may be statistically significant. Because of this, they suggested putting aside standardized residuals altogether.

Item Fit

Model fit takes the overall structure into consideration. If one was to remove some “misfit” items and re-run the Rasch analysis, the distribution would look more normal; however, there would still be items with high residuals. Because of this, the “model fit” approach is not a good way to examine item fit. A better way is to check the mean square. Unlike standardized residuals, the mean square is sample-size independent when data noise is evenly distributed across the population (Linacre, 2014). In a typical Winsteps output, “IN.MSQ” and “OUT.MSQ” stand for “infit mean square” and “outfit mean square.” “Mean square” is the Chi-square statistics divided by the degrees of freedom (df), or the mean of the squared residuals (Bond & Fox, 2015).

Table 4.5 is a crosstab 2 × 3 table showing the number of correct and incorrect answers to an item categorized by the skill level of test takers. At first glance this item seems to be problematic because while only 10 skilled test-takers were able to answer this item correctly, 15 less skilled test-takers answered the question correctly. Does this mean that the item is a misfit? To answer this question, the algorithm performs a Chi-square analysis. If the Chi-square statistic is statistically significant, meaning that the discrepancy between the expected cell count and the actual cell count is very large, then it indicates that the item might be a misfit.

Table 4.5 2 × 3 table of answer and skill level
Full size table

It is important to keep in mind that the above illustration is over-simplified. In the actual computation of misfit, examinees are not typically divided into only three groups; rather, more levels should be used. There is no common consent about the optimal number of intervals. Yen (1981) suggested using 10 grouping intervals. It is important to point out that the number of levels is tied to the degrees of freedom, which affects the significance of a Chi-square test. The degrees of freedom for a Chi-square test is obtained by (the number of rows) × (the number of columns). Whether the Chi-square is significant or not highly depends on the degrees of freedom and the number of rows/columns (the number of levels chosen by the software package). Hence, to generate a sample-free fit index, the mean-square (i.e. the Chi-square divided by the degrees of freedom) is reported.

Infit and Outfit

The infit mean-square is the Chi-square/degrees of freedom with weighting, in which a constant is put into the algorithms to indicate how much certain observations are taken into account. As mentioned before, in the actual computation of misfit there may be many groups of examinees partitioned by their skill level, but usually there are just a few observations near the two ends of the distribution. Do we care much about the test takers at the two extreme ends? If not, then we should assign more weight to examinees near the middle during the Chi-square computation (see Fig. 4.8). The outfit mean square is the converse of its infit counterpart: unweighted Chi-square/df. The meanings of “infit” and “outfit” are the same in the context of standardized residuals. Another way of conceptualizing “infit mean square” is to view it as the ratio between observed and predicted variance. For example, when infit mean square is 1, the observed variance is exactly the same as the predicted variance. When it is 1.3, it means that the item has 30% more unexpected variance than the model predicted (Lai et al., 2003).

Fig. 4.8
figure 8

Distribution of examinees’ skill level

Full size image

The objective of computing item fit indices is to spot misfits. Is there a particular cutoff to demarcate misfits and non-misifts? The following is a summary of how different levels of mean-square value should be interpreted (Linacre, 2017) (Table 4.6).

Table 4.6 Interpretation of different levels of mean-square values
Full size table

Many psychometricians do not recommend setting a fixed cut-off (Wang & Chen, 2005). An alternate practice is to check all mean squares visually. Consider the example shown in Fig. 4.9. None of the mean squares displayed in the dot plot is above 1.5 by looking at the numbers alone, we may conclude that there is no misfitted items in this example. However, by definition, a misfit is an item whose behavior does not conform to the overall pattern of items, and it is obvious from looking at the pattern of the data that one particular item departs from the others. As such, further scrutiny for this potential misfit is strongly recommended.

Fig. 4.9
figure 9

Dot plot of outfit mean squares

Full size image

According to Winsteps and Rasch Measurement Software (2010), if the mean square values are less than 1.0, the observations might be too predictable due to redundancy or model overfit. Nevertheless, high mean squares are a much greater threat to validity than are low mean squares. As such, it is advisable to focus on items with high mean squares while conducting misfit diagnosis (Bond & Fox, 2015; Bonne, Staver, & Yale, 2014).

A common question to ask may be whether these misfit indices agree with each other all the time, and which one we should trust when they differ from one another. Infit is a weighted method while outfit is unweighted. Because some difference will naturally occur, the question to consider is not whether items are different from one another. Rather, the key questions are: (1) To what degree do items differ from one another? (2) Do differences lead to contradictory conclusions regarding the fitness of certain items? Checking the correspondence between infit and outfit can be done by a scatterplot and Pearson’s r. Figure 4.10 shows that in this example there is a fairly good degree of agreement between infit and outfit statistics.

Fig. 4.10
figure 10

Scatterplot of the infit and outfit statistics

Full size image

Person Fit

As mentioned before, a Rasch output contains two clusters of information: a person’s theta and item parameters. In the former the skill level of the examinees is estimated, whereas in the latter the item attributes are estimated. The preceding illustration uses the item parameter output only, but a person’s theta (θ) output may also be analyzed, using the same four types of misfit indices. It is crucial to point out that misfits among person thetas are not just outliers, which represent over-achievers who obtained extremely high scores or under-achievers who obtained extremely low scores. Instead, misfits among person thetas represent people who have an estimated ability level that does not fit into the overall pattern. In the example of item misfit, we doubt whether an item is well-written when more low skilled students (15) than high skilled students (10) have given the right answer. By the same token, if an apparently low-skill student answers many difficult items correctly in a block of questions, there is some evidence for this student having cheated. The proper countermeasure to take, in this example, is to remove these participants from the dataset and re-run the analysis (Bonne & Noltemeyer, 2017).

Strategy

Taking all of the above into consideration, the strategy for examining the fitness of a test for diagnosis purposes is summarized as follows:

  1. 1.

    Evaluate the person fit to remove suspicious examinees. Use outfit mean squares, because when you encounter an unknown situation, it is better not to perform any weighting on any observation. If the sample size is large (e.g. >1,000), removing a few subjects is unlikely to make a difference. However, if a large chunk of person misfits must be deleted, it is advisable to re-compute the Rasch model.

  2. 2.

    If there are alternate forms or multiple sections in the same test, compare across these forms or sections by checking their AIC and BIC. If there is only one test, evaluate the overall model fit by first checking the outfit standardized residuals and second checking the infit standardized residuals. Outfit is more inclusive, in the sense that every observation counts. Create a scatterplot to see whether the infit and outfit model fit indices agree with one another. If there is a discrepancy, determining whether or not to trust the infit or outfit will depend on what your goal is. If the target audience of the test consists of examinees with average skill-level, an infit model index may be more informative.

  3. 3.

    If the model fit is satisfactory, examine the item fit in the same order with outfit first and infit second. Rather than using a fixed cut-off for mean square, visualize the mean square indices in a dot plot to detect whether any items significantly depart from the majority, and also use a scatterplot to check the correspondence between infit and outfit.

  4. 4.

    When item misfits are found, one should check the key, the distracters, and the question content first. Farish (1984) found that if misfits are mechanically deleted just based on chi-square values or standardized residuals, this improves the fit of the test as a whole, but worsens the fit of the remaining items.

Specialized Models

Partial Credit Model

Traditionally Rasch modeling was employed for dichotomous data only. Later it was extended to polytomous data. For example, if essay-type questions are included in a test, then students can earn partial credits. The appropriate Rasch model for this type of data is the partial credit model (PCM) (Masters, 1982). In a PCM the analyst can examine the step function for diagnosis. For example, if an item is worth 4 points, there will be four steps:

  • Step 1: from 0 to 1

  • Step 2: from 1 to 2

  • Step 3: from 2 to 3

  • Step 4: from 3 to 4

Between each level, there is a step difficulty estimate, also known as the step threshold, which is similar to the item difficulty parameter (e.g. How hard is it to reach 1 point from 0? How hard is it to reach 2 points from 1? …etc.). Because the difficulty estimate uses logit, distances between steps are comparable. For instance, if step3–step2 = 0.1 and step2–step1 = 0.1, then the two numbers are equal. Table 4.7 shows an example of the step function.

Table 4.7 Step function
Full size table

If the number of the step difficulty is around zero, this step is considered average. If the number is above 0.1, this step is considered hard. If the number is below zero, this step is considered easy. In this example, going from score = 0 to score = 1 is relatively challenging (Step difficulty = 0.6), reaching the middle step (score = 2) is easy (Step difficulty = −0.4), reaching the next level (score = 3) is even easier (Step difficulty = 0), but reaching the top (Score = 4) becomes very difficult (Step difficulty = 0.9). For example, for a Chinese student who doesn’t know anything about English, it will be challenging for him/her to start afresh, with no prior knowledge of English grammar. After he/she has built up a foundational knowledge in English, it will be easier to gradually improve his/her proficiency, but for him/her to master the English language at the level of Shakespeare, it would be very difficult.

Rating Scale Model

If the data are collected from a Likert-scaled survey, the most appropriate model is the rating scale model (RSM) (Andrich, 1978). Interestingly, although originally Andrich intended to develop RSM for evaluating written essays, like PCM it is now routinely used for Likert-scaled data (Bond & Fox, 2015). When a 4-point Likert scale is used, then “strongly agree” is treated as 4 points whereas the numeric value “1” is assigned to “strong disagree.” This approach models the response outcome as the probability of endorsing a statement. Figure 4.11 is an output by SAS’s graded response modeling. In each graph there are five ICCs corresponding to the numeric values from “strongly agree” to “strongly disagree.” In this case the θ represented by the X-axis (−4 to 4) is the overall endorsement of the idea or the construct. For example, if the survey aims to measure the construct “computer anxiety” and Question 1 is: “I am so afraid of computers I avoid using them,” it is not surprising to see that students who are very anxious about computing has a higher probability of choosing “strongly agree” (4). Question 3 is “I am afraid that I will make mistakes when I use my computer.” Obviously, this statement shows a lower fear of computers (the respondent still uses computers) than does Statement 1 (The respondent does not use computers at all), and thus it is more probable for students to choose “agree” (3) than “strongly agree” (4). However, in CTT responses from both questions would contribute equal points to the computer anxiety score. This example shows that Rasch modeling is also beneficial to survey analysis (Bond & Fox, 2015).

Fig. 4.11
figure 11

ICCs in the graded response model

Full size image

In SAS there is no direct specification of the partial credit model. PCM is computed through the generalized partial credit model (Muraki, 1992), in which the discrimination parameter is set to 1 for all items. In Winsteps both RSM and PCM are under the rating-scale family of models and therefore for both models the syntax is “Models = R.” Moreover, the average of the item threshold parameters is constrained to 0.

Debate Between Rasch and IRT

Rasch modeling has a close cousin, namely, item response theory (IRT). Although IRT and Rasch modeling arose from two independent movements in measurement, both inherited a common intellectual heritage: Thurstone’s theory of mental ability test in the 1920s (Thurstone, 1927, 1928). Thurstone realized that the difficulty level of a test item depends on the age or the readiness of the test-taker. Specifically, older children are more capable of answering challenging items than their younger peers. For this reason it would be absurd to assert that a 15-year old child who scored a ‘110’ on an IQ test is better than his 10-year old peer who earned 100 points on the same test. Hence, Thurstone envisioned a measurement tool that could account for both item difficulty and subject ability/readiness. Bock (1997), one of the founders of the IRT school, explicitly stated that his work aimed to actualize the vision of Thurstone. By the same token, Wright (1997), one of the major advocates of Rasch modeling, cited Thurstone’s work in order to support claims regarding the characteristics of Rasch modeling (e.g. uni-dimensionality and objective measurement).

The debate over Rasch versus IRT has been ongoing for several decades (Andrich, 2004). This debate reflects a ubiquitous tension between parsimonies and fitness in almost all statistical procedures. Since the real world is essentially “messy,” any model attempting to accurately reflect or fit “reality” will likely end up looking very complicated. As an alternative, some researchers seek to build elegant and simple models that have more practical implications. Simply put, IRT leans toward fitness whereas Rasch leans toward simplicity. To be more specific, IRT modelers might use up to three parameters. When the data cannot fit into a one-parameter model, additional parameters (such as the discrimination parameter (a) and the guessing parameter (g)) are inserted into the model in order to accommodate the data. Rasch modelers, however, stick with only one parameter (the item difficulty parameter), dismissing the unfit portion of their data as random variation. When the discrepancy between the data and the model exceeds minor random variation, Rasch modelers believe that something went wrong with the data and that modifying the data collection approach might produce a more plausible interpretation than changing the model (Andrich, 2011). In other words, IRT is said to be descriptive in nature because it aims to fit the model to the data. In contrast, Rasch is prescriptive for it emphasizes fitting the data into the model. Nevertheless, despite their diverse views on model-data fitness, both IRT and Rasch modeling have advantages over CTT.

Using additional parameters has been a controversial issue. Fisher (2010) argued that the discrimination parameter in IRT leads to the paradox that one item can be more and less difficult than another item at the same time. This phenomenon known as the Lord’s paradox. In the perspective of Rasch modeling, this outcome should not be considered a proper model because construct validity requires that the item difficulty hierarchy is invariant across person abilities. Further, Wright (1995) asserted that the information provided by the discrimination parameter is equivalent to the Rasch INFIT statistics and therefore Rasch modeling alone is sufficient. When guessing occurs in an item, in Wright’s view (1995) this item is poorly written and the appropriate remedy is to remove the item.

Historically, Rasch modeling has gained more popularity than IRT, because of its low demand in sample size, relative ease of use, and simple interpretation (Lacourly, Martin, Silva, & Uribe, 2018). If Rasch modeling is properly applied, a short test built by Rasch analysis can provide more reliable assessments than a longer test made by other methods (Embretson & Hershberger, 1999). Prior research showed that even as few as 30 items administered to 30 participants can produce valid assessment (Linacre, 1994). On the other hand, psychometricians warned that complex IRT models might result in variations of scoring. In some peculiar situations three-parameter IRT models might fail to properly estimate the likelihood functions (Hambleton, Swaminathan, & Rogers, 1991).

There is no clear-cut answer to this debate. Whichever model is more suitable depends on the context and the desired emphasis. For instance, many educators agree that assessment tests are often multidimensional rather than unidimensional, which necessitates multidimensional IRT models (Cai, Seung, & Hansen, 2011; Han & Paek, 2014; Hartig & Hohler, 2009). Further, 3-parameter modeling is applicable to educational settings, but not to health-related outcomes, because it is hard to imagine how guessing could be involved in self- or clinician-reported health measures (Kean, Brodke, Biber, & Gross, 2018). Nonetheless, when standardization is a priority (e.g. in an educational setting), Rasch modeling is preferred, because its clarity facilitates quick yet informed decisions.

Software Applications for Rasch Modeling

There are many software applications for Rasch modeling on the market (Rasch.org, 2019), but it is beyond the scope of this chapter to discuss all of them. This chapter only highlights two of these applications: SAS and Winsteps. SAS is by far the world’s most popular statistical package; needless to say, it is convenient for SAS users to utilize their existing resources for assessment projects. In addition, SAS offers academicians free access to the University Edition, which can be run across Windows and Mac OS through a Web browser. Winsteps has its merits, too. Before SAS Institute released PROC IRT, the source code of Winsteps was considered better-built than its rivals (Linacre, 2004); therefore it is highly endorsed by many psychometricians. The differences between SAS and Winsteps are discussed as follows.

As its name implies, PROC IRT includes both IRT and Rasch modeling, based on the assumption that Rasch is a special case of a one-parameter IRT model, whereas Winsteps is exclusively designed for Rasch modeling. PROC IRT in SAS and Winsteps use different estimation methods. Specifically, SAS uses marginal maximum likelihood estimation (MMLE) with the assumption that the item difficulty parameter follows a normal distribution, while Winsteps uses joint maximum likelihood estimation (JMLE). In SAS there are no limitations on sample size and the number of items, as long as the microprocessor and the RAM can handle them. In Winsteps the sample size cannot exceed 1 million and the maximum number of items is 6,000.

Both SAS and Winsteps have unique features that are not available in other software packages. For example, in CTT, dimensionality of a test is typically examined by factor analysis whereas unidimensionality is assumed in Rasch modeling (Yu, Osborn-Popp, DiGangi, & Jannasch-Pennell, 2007). In SAS’s PROC IRT an analyst can concurrently examine factor structure and item characteristics (Yu, Douglas, & Yu, 2015). In Winsteps good items developed in previous psychometric analysis can be inserted into a new test for item anchoring. By doing so all other item attributes would be calibrated around the anchors. Further, these item anchors can be put into alternate test forms so that multiple forms can be compared and equated based on a common set of anchors (Yu & Osborn-Popp, 2005).

In a simulation study, Cole (2019) found that there was virtually no difference between SAS and Winsteps for identifying item parameters (in data sets consisting of all dichotomous or all polytomous items, and in terms of average root mean squared errors (RMSE) and bias). Taking all of the above into consideration, the choice of which software application should be used depends on the sample size, the number of items, availability of resources, and the research goals, rather than upon accuracy of the output. SAS and Winsteps codes for different modeling techniques are shown in the appendix.

Conclusion

Rasch modeling is a powerful assessment tool for overcoming circular dependency observed in classical test theory. Based on the assumptions of uni-dimensionality and conditional independence, Rasch is capable of delivering objective measurement in various settings. Rasch analysis calibrates item difficulty and person ability simultaneously, in the fashion of residual analysis. After the data and the model converge by calibration, Rasch modelers can visualize the probability of correctly answering a question or endorsing a statement through item characteristic curves (ICC). In addition, the test designer can utilize item information functions (IIF) and test information function (TIF) to create alternate forms. One of the wonderful features of Rasch analysis is that the item and person attributes are put on the same scale (i.e. logit) and thus an analyst can examine whether a student and an exam can “match” each other, using the item-person map (IPM). Like every other analytical tool, diagnosis is an essential step in Rasch analysis. All Rasch modeling software packages, including SAS and Winsteps, provide users with both model-level and item-level fit indices. In addition to the Rasch dichotomous model, both SAS and Winsteps can run specialized models, such as the partial credit model (PCM) and the graded response model (GSM). Readers are encouraged to explore the functionality of these model by experimenting with the source codes at the appendix. Last but not least, the debate over Rasch vs. IRT has been ongoing for decades and the issue remains inconclusive. Different problems and different settings necessitate different solutions. It is advisable to keep an open mind to the strengths and the limitations associated with various modeling techniques.