Keywords

1 Introduction

In recent days, the study on microfluidic systems has become an important area of research for various potential applications in biomedical and chemical industry. Biomedical microelectromechanical systems or bioMEMS can accomplish sample injection, chemical reaction, separation, and detection in a single integrated microfluidic circuit [1]. Various techniques such as thermopneumatic, magnetohydrodynamic, piezoelectric, electrostatic, and electroosmotic pumping have been proposed for fluid delivery. Among these, the electroosmotic pumping is preferred because pumping a liquid through a very small channel requires a very large pressure difference, whereas it does not require any external pump, but needs electrodes to control the flow field. Due to the absence of moving parts and pulsating flows, ease of microfabrication, and a great degree of flow control, the electroosmotic pumping is very popular [2,3,4,5,6]. Therefore, it is important to understand the fundamental characteristics of electroosmotic flow (EOF) through microchannels for optimal design and efficient control and to ensure the reliability and the stability of the microfluidic devices of electroosmotic pumps. When an electrolytic solution is under no flow condition, the ions dissociate. Those ions having charge opposite to that of the surface are attracted by the surface. Thus, two layers of positively and negatively charged ions are formed near the surface which are called electric double layer (EDL). If a pressure gradient and an electric field are applied tangentially along such a charged surface, the ions in the diffuse layer will start moving under the action of the pressure field and body force exerted by the electric field, resulting in pressure-driven EOF [3].

In this connection, few literatures are studied. Masood Khan et al. [5] discussed the dynamics of an EOF in cylindrical domain. The linearized Poisson–Boltzmann equation and the Cauchy momentum equation were solved using the temporal Fourier and finite Hankel transforms. Ngoma and Erchiqui [7] investigated the liquid flow with the slip boundary condition in a microchannel between two parallel plates with imposed heat flux. They considered the combined effect of pressure-driven flow and electroosmosis. Jain and Jensen [8] presented an analytical investigation on the effects of electrostatic potential in microchannels. The energy equation was solved with the Nusselt number for constant wall heat flux and constant wall temperature boundary conditions and presented with analytic expressions over a wide range of operating conditions. Min et al. [9] analytically solved the fundamental characteristics of electroosmotic flow through rectangular pumping channels without the Debye–Huckel approximation. The Poisson–Boltzmann equation for the electric potential distribution and the momentum equation for the velocity profile are solved by averaging method. The zeta potential is experimentally measured by the streaming potential technique. They found that their method is applicable when the ratio of a half of the channel width to the EDL thickness is larger than 3.

It is observed from the above literature that conventionally, the electric potential distribution inside a microchannel is determined by a simplified analysis based on the Debye–Huckel linear approximation which is valid for small value of wall zeta potential (usually <25 mV). However, higher range of zeta potentials (100–200 mV) are frequently encountered in practical applications [9,10,11]. As a result, the accuracy level of the result may reduce. On the other hand, the analytical methods applied are complex, lengthy, and laborious. Hence, it is highly desirable to adopt a simple analytical method to study the fundamental characteristics of EOF through microchannels without the Debye–Huckel approximation. Hence, in the present work, homotopy perturbation method (HPM) as an analytical tool is considered to solve the Poisson–Boltzmann equation as it is a simple, powerful, and efficient solving technique, whereas the Navier–Stokes and the energy equations are also solved analytically for determination of velocity and temperature distributions, respectively, for flow within a microchannel between two parallel plates.

2 Description of the Physical Problem

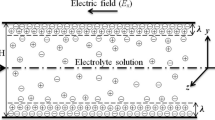
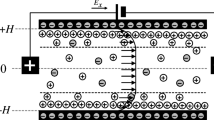
In the present work, a microchannel consisting of two parallel plates separated by a distance 2H is considered as shown in Fig. 1. The plate extends to infinity in x- and z-directions. So, property variation is considered in the y-direction. Because of the symmetry in the potential and velocity fields, the solution domain is reduced to a half section of the channel (as shown by the hatched area in Fig. 1). Two plate-type electrodes are placed apart by length L normal to the parallel plates such that an electric field is induced in the x-direction. A constant pressure gradient is also imposed in the x-direction to study combined effect of both the fields. The following assumptions are made for the mathematical formulation.

Fig. 1
figure 1

Geometry of parallel plate microchannel

Full size image

  • The liquid is a symmetric electrolyte, incompressible, Newtonian and the thermophysical properties are constant.

  • The flow is steady, laminar, and fully developed.

  • No-slip boundary condition and no wall temperature jump.

3 Mathematical Formulation

In the present study, a combined pressure-driven electroosmotic flow through a microchannel between two parallel plates is considered. The subsequent governing equations subjected to the respective boundary conditions are considered.

3.1 Poisson–Boltzmann Equation

The one-dimensional EDL field can be described by the Poisson–Boltzmann equation given as [8, 10, 12,13,14]

$$\partial^{2} \psi /\partial y^{2} = (2zen_{0} /\varepsilon )\sinh (ze\psi /k_{b} T)$$
(1)

where \(\psi\), z, e, \(n_{0}\),\(\varepsilon\),\(k_{b}\), and \(T\) are the electric potential due to EDL, valence of ions, electric charge, bulk ionic concentration, permittivity of vacuum, Boltzmann constant, and absolute temperature, respectively.

Equation (1) is subjected to the following boundary conditions at \(y = 0\), \(\partial \psi /\partial y = 0\) and at \(y = H\), \(\psi =\) wall zeta potential \((\xi )\).

3.2 Momentum Equation

The Navier–Stokes equation [8, 10] along the x-axis is considered by a balance between the shear stresses in the fluid, externally imposed constant pressure gradient, and electric field as

$$\mu (\partial^{2} u/\partial y^{2} ) - \partial P/\partial x + \rho_{f} E_{x} = 0$$
(2)

where \(\mu\), \(u\), \(\partial P/\partial x\), \(\rho_{f}\), and \(E_{x}\) are the dynamic viscosity, velocity in x-direction, pressure gradient in x-direction, local net charge density, and the electric field strength, respectively.

The above equation is subjected to the following boundary conditions at \(y = 0\), \(\partial u/\partial y = 0\) and at \(y = H\), \(u = 0\).

3.3 Energy Equation

The steady-state energy equation is given as [8, 10, 12,13,14]

$$u(\partial T/\partial x) = \alpha (\partial^{2} T/\partial y^{2} )$$
(3)

where \(\alpha = \rho C_{p} /\mu\) is thermal diffusivity.

The boundary conditions are given as at \(y = 0\), \(\partial T/\partial y = 0\) and at \(y = H\), where \(T\) is surface temperature.

4 Solution of the Governing Equations

The governing equations for electrical potential, velocity, and temperature distributions have been solved analytically.

4.1 Electric Potential Distribution

The governing Eq. (1) for electrical potential distribution has been solved by homotopy perturbation method (HPM). Equation (1) and its boundary conditions are non-dimensionalized by introducing the dimensionless variables as

$$Y = y/H,\,\Psi = ze\psi /(k_{b} T),\,{\rm Z} = 2ze\xi /(k_{b} T)$$

The non-dimensional form of Eq. (1) becomes

$$\partial^{2}\Psi /\partial Y^{2} = \lambda^{2} \sinh\Psi$$
(4)

where \(\lambda = \kappa H\) is the electrokinetic length and \(\kappa = \sqrt {[2z^{2} e^{2} n_{0} /(\varepsilon k_{b} T)]}\) is the inverse Debye–Huckel length.

The corresponding non-dimensional boundary conditions are written as at \(Y = 0\), \(\partial\Psi /\partial Y = 0\) and at \(Y = 1\), \(\Psi = {\rm Z}\).

In most of the existing work, the Debye–Huckel approximation is considered where \(\sinh\Psi\) in Eq. (4) is replaced by only \(\Psi\). It is already stated that this approximation holds good for small value of zeta potential. In the present study, the Debye–Huckel approximation is ignored to improve the accuracy level of results and to predict results for high range of zeta potential. Hence, in Eq. (4) instead of \(\Psi\), \(\sinh\Psi\) is considered. Hence, \(\sinh\Psi\) is expanded based on the Taylor series of expansion as

$$\sinh\Psi =\Psi +\Psi ^{3} /3! + \cdots$$
(5)

Substituting the above relation in Eq. (4) results in

$$\partial^{2}\Psi /\partial Y^{2} = \lambda^{2} (\Psi +\Psi ^{3} /3! + \cdots )$$
(6)

The homotopy considered is

$$\Psi ^{{\prime \prime }} - \omega^{2}\Psi + p[\left( {\lambda^{2} - \omega^{2} } \right)\Psi + \lambda^{2}\Psi ^{2} /3] = 0$$
(7)

where \(\Psi ^{{\prime \prime }} = \partial^{2}\Psi /\partial Y^{2}\), ω is a modified inverse Debye length, and \(p \in [0,1]\) is an embedding parameter, a small parameter in the homotopy perturbation method.

The power series in p used to find the solution of Eq. (7) is

$$\Psi =\Psi _{0} + p\Psi _{1} + \cdots$$
(8)

Substituting the above expression in Eq. (7) and arranging the coefficients of p powers, the following homotopy is obtained

$$p^{0} \left( {\Psi _{0}^{{\prime \prime }} - \omega^{2}\Psi _{0} } \right) + p^{1} [\Psi _{1}^{{\prime \prime }} - \omega^{2}\Psi _{1} - \left( {\lambda^{2} - \omega^{2} } \right)\Psi _{0} - \lambda^{2}\Psi _{0}^{\text{3}} /3!] = 0$$
(9)

Equating the coefficients of p0, p1 to zero gives

$$p^{0} :\Psi _{0}^{{\prime \prime }} - \omega^{2}\Psi _{0} = 0$$
(10)
$$p^{1} :\Psi _{1}^{{\prime \prime }} - \omega^{2}\Psi _{1} - \left( {\lambda^{2} - \omega^{2} } \right)\Psi _{0} - \lambda^{2}\Psi _{0}^{3} /3! = 0$$
(11)

Equation (10) is solved using the boundary conditions

$$\Psi _{0} \left( 1 \right) = {\rm Z},\,\Psi _{0}^{{\prime }} \left( 0 \right) = 0$$

and the resulting equation is

$$\Psi _{0} = {\rm Z}\cosh (\omega {\text{Y}})/\cosh (\omega )$$
(12)

Substituting the above expression in Eq. (11) and simplifying the equation give

$$\begin{aligned}&\Psi _{1}^{{\prime \prime }} - \omega^{2}\Psi _{1} - (\lambda^{2} - \omega^{2} ){\rm Z}\cosh (\omega {\text{Y}})/\cosh \omega\\&\quad - \lambda^{2} {\rm Z}^{3} [3\cosh \left( {\omega {\text{Y}}} \right) + \cosh \left( {3\omega {\text{Y}}} \right)]/[24\cosh^{3} \omega ] = 0 \end{aligned}$$
(13)

In order to eliminate \({\text{cosh(}}\omega {\text{Y)}}\) from Eq. (13), the coefficients are collected and equated to zero to predict the value of ω. Equation (13) becomes

$$\Psi _{1}^{{\prime \prime }} - \omega^{2}\Psi _{1} - \lambda^{2} {\rm Z}^{3} \cosh (3\omega {\text{Y}})/[24\cosh^{3} (\omega )] = 0$$
(14)

Now applying the boundary conditions

$$\Psi _{1} \left( 1 \right) = 0,\,\Psi _{1}^{{\prime }} \left( 0 \right) = 0$$

Eq. (14) is solved as

$$\Psi _{1} = [\lambda^{2} {\rm Z}^{3} /192\omega^{2} \cosh^{3} (\omega )][\cosh (3\omega {\text{Y}}) - \cosh (3\omega )\cosh (\omega {\text{Y}})/\cosh (\omega )]$$
(15)

Substituting the results of Eq. (12) and Eq. (15) in Eq. (8) and considering p = 1, the electric potential distribution is obtained as

$$\Psi = {\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right)$$
(16)

where \({\rm A}_{1} = {\rm Z}/\cosh \omega - \lambda^{2} {\rm Z}^{3} \cosh 3\omega /[192\omega^{2} \cosh^{4} \omega ]\) and \({\rm A}_{2} = \lambda^{2} {\rm Z}^{3} /[192\omega^{2} \cosh^{3} \omega ]\)

4.2 Velocity Distribution

The Navier–Stokes equation becomes (18)

$$\mu (\partial^{2} u/\partial y^{2} ) = \partial P /\partial {\text{x}} + (2zen_{0} /\lambda^{2} )E_{x} \partial^{2}\Psi /\partial Y^{2}$$
(17)

where \(\rho_{f} = - 2zen_{0} \sinh\Psi\) and \(\sinh\Psi = (\partial^{2}\Psi /\partial Y^{2} )/\lambda^{2}\).

Equation (17) is non-dimensionalized incorporating the following non-dimensional terms

$$U = u/u_{m} ,\Gamma _{1} = - (H^{2} /\mu u_{m} )\partial P/\partial x,E = E{}_{x}L/\xi ,\Gamma _{2} = 2zen_{0} \xi H^{2} /(\mu u_{0} L)$$

where \(u_{m}\) is the mean velocity.

Hence, the Eq. (17) for the velocity field is written as

$$\partial^{2} U/\partial Y^{2} = -\Gamma _{1} + (\Gamma _{2} E/\lambda^{2} )(\partial^{2}\Psi /\partial Y^{2} )$$
(18)

The corresponding non-dimensional boundary conditions become at \(Y = 0\), \(\partial U/\partial Y = 0\) and at \(Y = 1\), \(U = 0\).

Finally, the velocity profile is obtained by integrating Eq. (18) twice with respect to Y with the given boundary conditions as

$$U =\Gamma _{1} (1 - {\text{Y}}^{2} )/2 + (\Gamma _{2} EZ/\lambda^{2} )[\{ {\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right)\} /Z - 1]$$
(19)

The relation between \(\Gamma _{1}\) and \(\Gamma _{2}\) is determined from the definition of mean velocity as

$$\int\limits_{0}^{1} {U{\text{d}}Y} = 1$$
(20)

and obtained as

$$\Gamma _{2} = (\lambda^{2} /EZ)(1 -\Gamma _{1} /3)/[\{ {\rm A}_{1} \sinh \left( \omega \right)/(\omega ) + {\rm A}_{2} \sinh \left( {3\omega } \right)/(3\omega )\} /Z - 1]$$
(21)

Now, the skin friction coefficient Cf is defined as [8]

$$C_{f} = 2\tau_{w} /(\rho U^{2} )$$
(22)

The product CfRe is obtained as

$$C_{f} \text{Re} = 8U^{\prime}(1)$$
(23)

where \(\text{Re} = \rho u_{m} (4H)/\mu\) is the Reynolds number.

4.3 Temperature Distribution

Equation (3) for temperature field is simplified by performing scale analysis as

\(\dot{q}^{\prime\prime} \sim (\dot{m}c_{p} \Delta T/A) \sim \rho c_{p} u_{m} \Delta T\) and \(\dot{q}^{\prime\prime} \sim h\left( {T_{m} - T_{s} } \right)\)

where \(\dot{q}^{\prime\prime}\), \(\dot{m}\), \(C_{p}\), \(\Delta T\), \(A\), \(\rho\), \(h\), and \(T_{m}\) are the wall heat flux, mass flow rate of liquid, specific heat, temperature scale, area normal to heat flow, convective heat transfer coefficient, and mean temperature, respectively.

From the above relations, it is observed that

$$\partial T/\partial x = \Delta T/\Delta x = \dot{q}^{\prime\prime}/(\rho u_{m} c_{p} H)$$
(24)

where \(\Delta x\) is the length scale in x-direction.

Combining Eqs. (3) and (24), the relation obtained is as follows

$$\partial^{2} T/\partial y^{2} = u\dot{q}^{\prime\prime}/(\alpha \rho u_{m} c_{p} H)$$
(25)

Equation (25) is non-dimensionalized considering

$$\Phi = (T - T_{s} )/(T_{m} - T_{s} )\,{\text{and}}\,Nu = (4H)(h)/K$$

and is written as

$$\partial^{2}\Phi /\partial Y^{2} = (Nu)(U)/4$$
(26)

The corresponding boundary conditions become at \(Y = 0\), \(\partial\Phi /\partial Y = 0\) and at \(Y = 1\), \(\Phi = 0\).

Substituting the expression (Eq. (19)) for velocity distribution in Eq. (26) gives

$$\begin{aligned}&\partial^{2}\Phi /\partial Y^{2} = (Nu/4)[\Gamma _{1} (1 - {\text{Y}}^{2} )/2 + (\Gamma _{2} EZ/\lambda^{2} )\\&\quad [\{ {\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right)\} /Z - 1]] \end{aligned}$$
(27)

Thereafter, the Eq. (27) is integrated twice with respect to Y with the given boundary conditions to yield the temperature distribution as follows:

$$\begin{aligned}\Phi & = (Nu/4)[\Gamma _{1} ({\text{Y}}^{2} /4 - {\text{Y}}^{4} /24 - 5/24) + (\Gamma _{2} EZ/\lambda^{2} )[\{ 9{\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) - 9{\rm A}_{1} \cosh \left( \omega \right) \\ & \quad + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right) - {\rm A}_{2} \cosh \left( {3\omega } \right)\} /(9Z\omega^{2} ) + (1 - {\text{Y}}^{2} )/2]] \\ \end{aligned}$$
(28)

The mean temperature is defined as

$$\int\limits_{0}^{1} {U\Phi {\text{d}}Y = 1}$$
(29)

Finally, the expression of Nusselt number, Nu, is determined at the wall by substituting Eqs. (19) and (28) in the Eq. (29) and written as

$$\begin{aligned} Nu & = 4/\int_{0}^{1} {\Gamma _{1} (1 - {\text{Y}}^{2} )/2 + (\Gamma _{2} EZ/\lambda^{2} )[\{ {\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right)\} /Z - 1]} \\&\quad\quad [\Gamma _{1} ({\text{Y}}^{2} /4 - {\text{Y}}^{4} /24 - 5/24) + (\Gamma _{2} EZ/\lambda^{2} )[\{ 9{\rm A}_{1} \cosh \left( {\omega {\text{Y}}} \right) \\&\quad - 9{\rm A}_{1} \cosh \left( \omega \right) + {\rm A}_{2} \cosh \left( {3\omega {\text{Y}}} \right) - {\rm A}_{2} \cosh \left( {3\omega } \right)\} /(9Z\omega^{2} ) + (1 - {\text{Y}}^{2} )/2]]d{\text{Y}} \\ \end{aligned}$$
(30)

5 Results and Discussion

Finally, a MATLAB program is developed to solve the governing equation. The result obtained is presented in a comparative way with numerical method (FDM) and existing result to check the accuracy level of the proposed work.

In Fig. 2a, b, the potential distributions in the Y-direction for an electrokinetic length of 10 are presented at zeta potential values of 1 and 3, respectively. It is observed that the proposed result is in close agreement with the numerical solution for both the zeta potential values of 1 and 3. For smaller value of zeta potential (i.e., Z = 1), the solution based on the Debye–Huckel approximation agrees well with the numerical solution as shown in Fig. 2a whereas deviates more in Fig. 2b for Z = 3. Hence, the proposed method can be used for a large range of zeta potential.

Fig. 2
figure 2

Non-dimensional potential distribution a Z = 1 and b Z = 3 for \(\lambda = 10\)

Full size image

The velocity distribution obtained for the combined pressure-driven electroosmotic flow is compared with the existing work by Jain and Jansen [8] and numerical results in Fig. 3a, b. The proposed results show close agreement with the numerical method for Z = 1 and 3, whereas the existing work shows a little deviation from the numerical method close to the plate surface for Z = 3 as shown in Fig. 3b. This deviation may be due to the effect of the Debye–Huckel approximation considered in the existing work. Hence, the proposed results can predict the velocity distribution for higher values of zeta potential.

Fig. 3
figure 3

Non-dimensional velocity distribution a Z = 1 and b Z = 3 for \(\lambda = 10\)

Full size image

Figure 4a, b represents the temperature distribution for an electrokinetic length of 10 and zeta potential values of 1 and 3. Here the solution based on the proposed method is compared with the existing work by Jain and Jansen [8] and numerical results. It is observed that the proposed result is in close agreement with the numerical result for both the zeta potential values of 1 and 3. As a consequence of considering the Debye–Huckel approximation in the existing work, it shows a little deviation from the numerical result close to the plate surface for Z = 3 as shown in Fig. 4b. Hence, the proposed method can predict the temperature distribution for higher values of zeta potential.

Fig. 4
figure 4

Non-dimensional temperature distribution a Z = 1 and b Z = 3 for \(\lambda = 10\)

Full size image

In Fig. 5a, b, the product CfRe and the Nu are presented, respectively, as functions of \(\lambda\) for Z = 1, 2, and 3. It is seen that for a particular value of Z the value of CfRe decreases with increase in \(\lambda\). It has also been observed for a value of \(\lambda\), the CfRe product increases with rise in Z values. This can be attributed to the fact that on increasing the value of Z, the presence of EDL is felt in a region farther away from the wall which enhances the viscosity, and therefore, increases the value of CfRe. The variation of Nu with \(\lambda\) follows the same pattern as that of CfRe.

Fig. 5
figure 5

Variation of a CfRe product and b Nu with \(\lambda\) for Z = 1, 2, and 3

Full size image

6 Conclusion

The present work investigates an analytical solution based on the homotopy perturbation method to analyze the characteristics of combined pressure-driven electroosmotic flow between two parallel plates. The electric potential, velocity, and temperature distributions are obtained by solving the Poisson–Boltzmann equation without Debye–Huckel approximation, the Navier–Stokes equation, and energy equation, respectively. The homotopy perturbation method is used to solve the Poisson–Boltzmann equation. Finally, the Nusselt number has been determined. The proposed results for potential, velocity, and temperature fields are presented with an existing work and numerical method for Z = 1 and 3 for an electrokinetic length (\(\lambda\)) of 10. It is seen that the proposed method shows good agreement with the numerical method for Z = 1 and 3. The Nusselt number is presented with \(\lambda\) for Z = 1, 2, and 3.