Kinematics and Singularity Analysis of a Novel Uncoupled 2-DOF Rotational Parallel Mechanism

Abstract

The paper presents a novel uncoupled rotational parallel mechanism with two degrees of freedom (DOFs), which consists of a moving platform connected to a fixed base by two kinematical limbs. Based on the position and orientation characteristics method, kinematic output characteristics and mobility of the mechanism are analyzed and calculated. Mathematical models of the orientation and angular velocity of the mechanism are established in terms of the actuated wrench screw theory and the closed vector approach. Singularity analysis is performed in terms of the linear dependence of the kinematic screw system and constraint screw system, respectively, and all singular configurations are given as well.

1 Introduction

According to the differences of output motion characteristics of the moving platform, parallel mechanism can be divided into pure translational [1], pure rotational [2, 3] and hybrid types [4, 5]. Among them, the moving platform of the pure rotational parallel mechanism with two or three degrees of freedom can change the posture of the object in space to obtain the expected motion.

Generally, parallel mechanisms have strong motion coupling, which is beneficial to improve the rigidity and load carrying capacity of the mechanism, and which also causes some problems such as small working space, complex kinematics, and difficult control design. Therefore, decoupled parallel mechanism has become one of the hot spots in this field [6,7,8]. Uncoupled parallel mechanism is one special type during the decoupling parallel mechanisms. Its input-output motion has a one-to-one control relationship, which makes the kinematics and dynamic equations very simple and the control design is very easy. Xu [9] proposed two conditions for the full decoupling of two rotational DOFs of 2R1T and 2R PMs with three branches, including a just constraint branch. Jin [10] designed the 2T2R and 3T2R parallel mechanisms with large decoupled output rotational angles by using Lie group theory, and analyzed the fixed posture working space and posture space of the mechanism. Zhang [11] proposed an uncoupled 2T1R parallel mechanism and discussed its kinematic isotropic condition. This paper proposes a novel uncoupled two-rotational parallel mechanism. Kinematic problems and singular configurations of the mechanism are studied in detail.

2 Structural Design and Output Characteristics Analysis

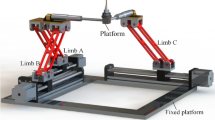
The novel parallel mechanism is shown in Fig. 1, which consists of a moving platform, a fixed base and two single open chains connected to two platforms. The arrangement of the first limb from the base to the platform is followed by rotational joint R₁₁, universal joint U₁₂, prismatic pair P₁₃, and universal joint U₁₄. In order to facilitate structural description of the mechanism, two universal joints U₁₂ and U₁₄ are replaced by rotational joint R₁₂ and R₁₃, and rotational joints R₁₅ and R₁₆, respectively.

Fig. 1.

Diagram of RR-RUPU parallel mechanism

In the first kinematic chain, axes of the joints R₁₁ and R₁₂ are parallel to each other, axes of the joints R₁₃ and R₁₅ are parallel to each other and perpendicular to the motion direction of the prismatic pair P₁₃. So the first chain can be recorded as . The arrangement of the second limb from the base to the platform is rotational joints R₂₁ and R₂₂ in sequence and their axes intersect perpendicularly. This chain can also be recorded as ${\text{SOC}}\left\{ - \right.{\text{R}}_{21} \bot {\text{R}}_{22} \left. - \right\}$. The assembling conditions of the two limbs are as follows: the axes of joints connected to the base are perpendicular to each other, and the axes of joints attached to the platform are parallel. The first revolute joint in each limb is selected as the actuated joint. The position and orientation characteristic sets M_b1 and M_b2 of the first and the second limbs can be written out, respectively, and have

$$ M_{{{\text{b}}1}} = \left[ {\begin{array}{*{20}c} {t^{3} } \\ {r^{2} / / ({R}_{ 1 5} ,{R}_{ 1 6} )\cup r^{1} / /{R}_{ 1 1} } \\ \end{array} } \right] $$

(1)

$$ M_{{{\text{b}}2}} = \left[ {\begin{array}{*{20}c} {t^{0} } \\ {r^{2} / / ({R}_{ 2 1} ,{R}_{ 2 2} )} \\ \end{array} } \right] $$

(2)

where, the right superscript numerals denote the characteristic degree of freedom (DOF) of the limb. For example, $r^{2} / /\left( {R_{15} ,R_{16} } \right)$ denotes that there are two rotational DOFs in the plane determined by the axes of R₁₅ and R₁₆, and $t^{0}$ denotes that the number of translational DOF is 0. Therefore, the position and orientation characteristic set of the mechanism shown in Fig. 1 is as follows

$$ M_{\text{b}} = M_{{{\text{b}}1}} \cap M_{{{\text{b}}2}} = \left[ {\begin{array}{*{20}c} {t^{0} } \\ {r^{2} / / ({R}_{ 2 1} ,{R}_{ 2 2} )} \\ \end{array} } \right] $$

(3)

Formula (3) shows that the platform has only two-dimensional rotational DOFs rotating around the axes of the joints R₂₁ and R₂₂. It is obvious that there is without any independently translational mobility for the mechanism.

The DOF of the parallel mechanism can be calculated by Eq. (4), and

$$ F = \sum\limits_{i = 1}^{m} {f_{i} } - \hbox{min} \sum\limits_{j = 1}^{v} {\xi_{j} } $$

(4)

where, F is the DOF of the mechanism; m is the number of joints, $f_{i}$ is the DOF of the ith joint, $v$ is the number of independent loops, $\xi_{j}$ is the number of independent displacement equations of the jth loop. For the mechanism shown in Fig. 1, m = 8, υ = 1, $\xi_{1}$ = 6, so we get F = 2. The calculation result is consistent with the previous analysis, i.e., the mechanism only has two rotational DOFs in space.

3 Kinematic Analysis of the Mechanism

3.1 Orientation Analysis

Three-dimensional CAD model of the parallel mechanism is shown in Fig. 2. The fixed coordinate system $O - xyz$ is attached on the base. Origin point O is located at the intersection of two rotational joints of the second limb, z-axis coincides with the axis of joint R₂₁, and x-axis is parallel to the axis of joint R₁₁. The moving coordinate system $P - uvw$ is fixed on the platform, its origin point P coincides with the point O, v-axis coincides with the axis of joint R₂₂ and w-axis is perpendicular to the platform. At the initial configuration, the axes of the two coordinate systems coincide with each other. Let $q_{11}$ and $q_{21}$ be the input angular displacement of the two actuated joints R₁₁ and R₂₁, respectively. $\alpha$ and $\beta$ are the orientation angles of the platform rotating around the v-axis and the z-axis. $\beta$ is the length of the active rod in the first limb, $r$ represents the size of the platform structure, which is measured between joints R₁₆ and R₂₂.

Fig. 2.

CAD model of the novel parallel mechanism

The local coordinate system $O_{1} - x_{1} y_{1} z_{1}$ is fixed on the base. Its origin point $O_{1}$ lies on the axis of joint R₁₁ and x₁ axis coincides with it. $z_{1}$ axis is perpendicular to the platform, as shown in Fig. 2.

The kinematic screw system of the first limb in system $O_{1} - x_{1} y_{1} z_{1}$ is written as

(5)

where, $L_{ij}$ and $M_{ij}$ are the direction vector parameters of screw corresponding to the jth joint in the ith chain, $P_{ij}$, $Q_{ij}$ and $R_{ij}$ are the position parameters of screw .

According Eq. (5), we know that it is 6-system kinematic screw for the first limb, so there is no any reciprocal screw. In system $O - xyz$, the kinematic screw system of the second limb is as

(6)

From formula (6), the order of kinematic screw system is 2, so there are 4 reciprocal screws for the second chain, and have

(7)

If the actuated joint of the first limb is locked, the kinematic screw system composed of the rest joints is

(8)

Based on the reciprocal product principle, it can be found that the reciprocal screw of is obtained as

(9)

where, ${\boldsymbol{S}}$ is the direction vector of screw , ${\boldsymbol{S}}_{0}$ is the dual part of ${\boldsymbol{S}}$, $P_{a1}$ and $Q_{a1}$ are non-zero parameters related to the position of . In terms of the definition of the actuation screw, we know that is the driving force applied to the moving platform by the actuated joint R₁₁, and its direction is parallel to the z-axis.

For the mechanism, the forward orientation solution is to find the posture angles ($\alpha$ and $\beta$) of the platform if the input angular displacements ($q_{11}$ and $q_{21}$) of the actuated joints are known. As shown in Fig. 3, point A is the intersection of two rotational axes in joint U₁₂, point B is the intersection of the moving direction of pair P₁₃ and the vertical axis of the joint U₁₂, point C is the intersection of pair P₁₃ and the vertical axis of the joint U₁₄, point D is the intersection of two axes in U₁₄. Without losing generality, vector OD can be used to describe the posture angle of the platform.

Fig. 3.

Closed vector polygon diagram

In Fig. 3, the vectors OD, ${\boldsymbol{OO}}_{ 1}$, ${\boldsymbol{O}}_{ 1} {\boldsymbol{A}}$, AB, BC and CD form a closed vector polygon. Then, have

$$ {\boldsymbol{OD = OO}}_{ 1} + {\boldsymbol{O}}_{ 1} {\boldsymbol{A}} + {\boldsymbol{AB}} + {\boldsymbol{BC}} + {\boldsymbol{CD}} $$

(10)

Using the original part S of the screw to multiply both sides of the Eq. (10), yields

$$ {\boldsymbol{S}}\bullet {\boldsymbol{OD = S}}\bullet{\boldsymbol{OO}}_{ 1} + {\boldsymbol{S}}\bullet{\boldsymbol{O}}_{ 1} {\boldsymbol{A}} + {\boldsymbol{S}}\bullet{\boldsymbol{AB}} + {\boldsymbol{S}}\bullet{\boldsymbol{BC}} + {\boldsymbol{S}}\bullet{\boldsymbol{CD}} $$

(11)

Rearranging Eq. (11), we have

$$ r\sin \alpha = O_{1z} + l\sin q_{11} + a + b $$

(12)

where, $O_{1z}$ denotes the coordinate value point $O_{1}$ along z-axis in system $O - xyz$, and a and b denote the component of vector AB and CD along z axis, respectively.

Since parameters $O_{1z}$, $a$ and $b$ are only related to the structure size of the mechanism, $O_{1z} + a + b = 0$ can be meet through the reasonable design. Therefore, Eq. (12) can be simplified as follows

$$ r\sin \alpha = l\sin q_{11} $$

(13)

Thus, the posture angle $\alpha$ of the platform is

$$ \alpha = arc\sin (l\sin q_{11} /r) $$

(14)

From Fig. 3, we know that the posture angle $\beta$ of the platform is only related to the angular displacement $q_{21}$ of the actuated joint R₂₁ in second limb. Then, we have

$$ q_{21} = \beta + c_{0} $$

(15)

where, $c_{0}$ is the initial angle of the platform around the z-axis.

Since both systems $O - xyz$ and $P - uvw$ are defined as coinciding to each other at the initial position, we get $c_{0} = 0$. Thus formula (15) can be rewritten as follows

$$ \beta = q_{21} $$

(16)

3.2 Angular Velocity Analysis

Differentiating Eqs. (13) and (16) with respect to time and rearranging them, the angular velocity equation is obtained

$$ {\boldsymbol{\omega }} = {{\boldsymbol{J}\dot{\boldsymbol{q}}}} $$

(17)

where, ${\boldsymbol{\omega }} = \left[ {\begin{array}{*{20}c} {{\boldsymbol{\omega }}_{v} } & {{\boldsymbol{\omega }}_{z} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} {\dot{\alpha }} & {\dot{\beta }} \\ \end{array} } \right]^{\text{T}}$ is the output velocity vector of the platform, ${\boldsymbol{\dot{q}}} = \left[ {\begin{array}{*{20}c} {\dot{q}_{11} } & {\dot{q}_{21} } \\ \end{array} } \right]^{\text{T}}$ is the input velocity vector of the actuated joints, J is the velocity Jacobian matrix, and have

$$ {\boldsymbol{J}} = \left[ {\begin{array}{*{20}c} {\frac{{l\cos q_{11} }}{r\cos \alpha }} & 0 \\ 0 & 1 \\ \end{array} } \right] $$

(18)

Formula (18) shows that the Jacobian matrix J is diagonal, there is a one-to-one control mapping relationship between the inputs and the outputs, so the mechanism has uncoupled kinematics characteristics. Especially the second element on the diagonal line of the matrix is equal to 1, so the condition $\omega_{z} = \dot{q}_{21}$ is satisfied.

4 Singularity Analysis

Singularity is the inherent property of parallel mechanism. When the structure size of the mechanism is given, the singular configurations will be determined accordingly. Fang and Tsai [12] classified the singular types of parallel mechanisms into three types: limb singularity, actuation singularity and platform singularity.

4.1 Limb Singularity

The occurrence of this kind of singularity is related to the order of limb kinematic screw system, so it is called limb singularity. When the order of the kinematic screw system changes, the order of the constraint screw system also changes, which will lead to instantaneously gain or lose one or more degrees of freedom for the mechanism.

Formula (6) shows that the kinematic system of the second limb is always two-system, so the limb will not have any singular form. Formula (5) shows that the kinematic screw system of the first limb is six-system, and the union of the kinematic screw systems is equivalent to a square matrix ${\boldsymbol{A}}$. Therefore, singularity of the mechanism is determined that matrix ${\boldsymbol{A}}$ is full rank or not.

$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & {l\sin q_{11} } & { - l\cos q_{11} } \\ 0 & 0 & 1 & {l\cos q_{11} } & 0 & 0 \\ 0 & 0 & 0 & {L_{14} } & {M_{14} } & 0 \\ 0 & 0 & 1 & {P_{15} } & {Q_{15} } & 0 \\ { - \sin \beta } & {\cos \beta } & 0 & {P_{16} } & {Q_{16} } & {R_{16} } \\ \end{array} } \right] $$

(19)

If matrix ${\boldsymbol{A}}$ is not ranked, the kinematic screw system will be linearly dependent. In a result, the determinant $\det ({\boldsymbol{A}})$ is equal to zero. We know that the elementary transformation of a matrix does not affect the rank of the matrix, that is to say, it does not affect whether the determinant is zero or not. According to the method of matrix block calculation, the determinant value of matrix ${\boldsymbol{A}}$ can be calculated as

$$ \det ({\boldsymbol{A}}) = \det ({\boldsymbol{E}})\det ({\boldsymbol{F}}) $$

(20)

Where ${\boldsymbol{E}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 1 & 0 & { - l\cos q_{11} } \\ { - \sin \beta } & {\cos \beta } & {R_{16} } \\ \end{array} } \right]$, ${\boldsymbol{F}} = \left[ {\begin{array}{*{20}c} {L_{14} } & {M_{14} } & 0 \\ {P_{15} } & {Q_{15} } & 1 \\ {l\cos q_{11} } & 0 & 0 \\ \end{array} } \right]$.

If anyone of the matrices E or F is under-rank, then the matrix A will be under-rank. Singularity of the mechanism can be analyzed as follows.

Type 1.

Matrix E is under-rank

Based on matrix E, we get $\det ({\boldsymbol{E}}) = l\cos q_{11} \cos \beta$. If $\det ({\boldsymbol{E}}) = 0$, then $\beta = \pm \pi /2$ or $q_{11} = \pm \pi /2$. When $\beta = \pm \pi /2$, screws , and are parallel to each other and also parallel to screw of the second limb, see Fig. 4.

Fig. 4.

Singular configuration at $\beta = \pi /2$

When the actuated joint of the first limb is locked, the rotation element of the orientation feature set of the first limb is $M_{{{\text{b}}1}}^{r} = [r^{2} //(R_{15} ,R_{16} ) ]$, which means that the platform still has the mobility rotating around the $v$ axis. The singularity can be avoided by setting the distance between the two universal joints in the first limb.

When $q_{11} = \pm \pi /2$, the kinematic screw system can be computed by substituting it into formula (5). Then, the constraint screw of the limb is obtained, and have

(21)

Formula (21) represents a zero-pitch screw parallel to z axis, which constrains the movement of the first limb along z-axis. It also implies that the platform loses the ability to translate along the same direction. At last, the rotational mobility around joint R₂₂ of the platform is disappear. Due to the structural constraint, the singular configuration at $q_{11} = - \pi /2$ does not occur in the assembly condition shown in Fig. 2, and the singular configuration at $q_{11} = \pi /2$ is shown in Fig. 5.

Fig. 5.

Singular configuration at $q_{11} = \pi /2$

Type 2.

Matrix F is under-rank

Based on matrix F, we have

$$ \det ({\boldsymbol{F}}) = M_{14} l\cos q_{11} $$

(22)

If $\det ({\boldsymbol{F}}) =$ 0, then we get $q_{11} = \pm \pi /2$ or $M_{14} = 0$. When $q_{11} = \pm \pi /2$, the same results will be obtained like type 1. When $M_{14} = 0$, kinematic screw of pair P₁₃ can be rewritten as  = $[\begin{array}{*{20}c} 0 & 0 & {0;} & 1 & 0 & 0 \\ \end{array} ]^{{\begin{array}{*{20}c} {\text{T}} \\ \end{array} }}$, which is an infinite pitch screw parallel to x axis. At this configuration, screws , and are coplanar and linearly dependent so that the limb kinematic singularity occurs, shown in Fig. 6.

Fig. 6.

Singular configuration when $M_{14} = 0$

4.2 Actuation Singularity Analysis

When the actuated joints of two limbs are locked at the same time, the constraint screws and of two limbs can be obtained in terms of the principle of reciprocal production, and have

(23)

(24)

Rearranging and into a matrix G, yields

(25)

After dividing into four sub-blocks, we know if and only if the second sub-block matrix on the main diagonal is not full of rank, the matrix G is under-rank. At this condition, we have $\beta = q_{11} = \pm \pi /2$. There are total 4 sets of singular configurations, i.e.,

• (a) $\beta = \pi /2,$ $q_{11} = \pi /2$; (b) $\beta = - \pi /2,$ $q_{11} = \pi /2$

• (c) $\beta = \pi /2,$ $q_{11} = - \pi /2$; (d) $\beta = - \pi /2,$ $q_{11} = - \pi /2$.

Due to the structural constraints of the mechanism, the configurations (c) and (d) do not occur under the assembly condition shown in Fig. 2.

Based on the definition of the actuation screw, represented by the Eq. (24) is the driving force spiral applied to the platform by joint R₁₁ through the first limb. If the R₁₁ is locked, the constraint screw is linearly dependent to the constraint screw . So the platform loses the DOF rotating around v-axis. When $\beta = - \pi /2,$ and $q_{11} = \pi /2$, singular configuration is shown in Fig. 7.

Fig. 7.

Singular configuration when $\beta = - \pi /2,$ and $q_{11} = \pi /2$

4.3 Platform Singularity Analysis

When the constraint screws of the mechanism are linear dependence, the platform will lose some ability to constraint its motions. In a result, one or more unexpected degrees of freedom will produce. From formula (7), we know that the constraint screw system applied by the limbs to the platform contains three linear independent zero-pitch screws and one infinite-pitch screw. When the assembly form of the mechanism is given as Fig. 2, there will be no platform singularity.

5 Conclusions

• (1) A novel uncoupled two-rotational parallel mechanism is designed in this paper. The kinematic output characteristics of the mechanism are analyzed. Mathematical models of the kinematic problems are established.

• (2) Singularity of the mechanism is discussed, including limb singularity, actuation singularity and platform singularity. The singular configurations are also given. The research provides a theoretical basis for the practical application of the mechanism.