Kinematics and Dynamics Simulation Analysis of a 3-DOF Parallel Mechanism for Application in Hybrid Machine

Abstract

A novel parallel mechanism with one translational and two rotational coupling degrees of freedom, which can be utilized as the main body module for application in hybrid kinematic machine, is proposed. The inverse kinematics is systematically established based on the closed-loop vector method. In terms of the principle of virtual work and d’Alembert’s formulation, the dynamics formulation is deduced in sequence. Finally, the illustrative simulation example is conducted to demonstrate the analytic results of the kinematics and dynamics, and the analytical solutions are verified by Simulink and Recurdyn collaborative simulation. Simultaneously, the dynamic dexterity is further conducted to evaluate the performance, and the results show that the proposed parallel mechanism has greater dynamic performance, which can be demonstrated practically by the alternative application of the parallel kinematic module for the hybrid machine tool.

1 Introduction

Serial mechanisms and parallel mechanisms are two prime types of robots widely employed in various fields of both academy and practice such as kinematic machine tool, surgical robot, pick and place robot, and so on [1,2,3]. Serial mechanisms connected to each other in serial form have open loop structure which leads to lower precision, poor repeatability, as well as lower stiffness. In contrast, parallel mechanisms have taken more attention by domestic and foreign scholars due to their advantages such as high stiffness, lower inertia, high precision, and good dynamic characteristics over serial mechanisms. In general, the driving devices are installed at the fixed platform or a position close to the fixed platform, so that the moving components is light in weight and high in precision, good dynamic response, moreover, the fully symmetrical parallel mechanism has good isotropy. According to these characteristics, the parallel mechanism has been widely used in fields requiring high stiffness and high precision. Unfortunately, parallel mechanisms have inherent limitations such as small and complex workspace, especially the parallel mechanisms with translational and rotational coupling degrees of freedom, which is a fatal disadvantage and limit its application. In which of the situations, combining the advantages of parallel mechanisms and serial mechanisms, hybrid mechanisms are being developed in manufacturing and engineering fields in recently years [4, 5].

Tsai et al. [6] introduced a new hybrid machine which typically consisted of a position mechanism and an orientation mechanism that can be arranged in series or in parallel to achieve many various machine centers. Fully parallel mechanisms have relatively very limited workspace, especially in terms of orientation characteristics. Fully serial machines have a problem of error accumulation, so a modular method to construct a post-process system for a novel hybrid parallel serial five axis machine tool is proposed in [7]. Gao et al. [8] developed a five-axis hybrid computer numerical control machine by integrating an X-Y gantry system on the basis of parallel manipulator, and the inverse kinematics and optimization of the parallel manipulator were mathematically analyzed. Chen et al. [9] proposed a hybrid machining center including a three degree of freedom parallel platform and traditional computer numerical control X-Y table, and pointed that it is a trend for machine to be reconfigurable hybrid machine for the fabrication of complex and precision products. Coppola et al. [10] addressed a 6-DOF reconfigurable hybrid parallel manipulator for sustainable manufacturing, and a systematical kinematics, orientation workspace, singularity, and stiffness are developed in detail. Xie et al. [11] presented a novel redundant three degrees of freedom parallel kinematic mechanism with high rotational capability, investigated the motion/force transmissibility performance, and applied the parallel module to construct a redundant hybrid machine for freedom surface. Sun et al. [12] investigated a novel 5-axis hybrid reconfigurable robot named Tricept-IV, including one four degrees of freedom hybrid module and one two degrees of freedom end effector, and demonstrated a method of workspace decomposition applied in the dimensional synthesis of a 4-DOF hybrid module. In general, the hybrid architecture contains several different configuration type such as parallel-serial, parallel-parallel, serial-parallel, and so on, therefore, the mechanism proposed in this paper is no exception.

The rest of this paper is organized as follows. Section 1 has provided the introduction. In Sect. 2, the proposed parallel mechanism is described in detail, and presented the candidate application in hybrid machine. In Sect. 3, the inverse kinematics including position, velocity and acceleration are derived. Next, the dynamics is deduced on the basis of the principle of virtual work in Sect. 4. Section 5 the simulation comparative analysis based on the Simulink and Recurdyn are conducted, some simulation results and dynamic dexterity performance are depicted. Finally, Sect. 6 provides contributions and suggestions for further work.

2 Architecture Description

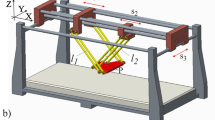
The parallel mechanism proposed in this paper includes a fixed platform, a moving platform, and four limbs with variable lengths (two RPU configuration kinematic legs l_i(i = 1, 3), and two SPR configuration kinematic legs l_i(i = 2, 4)), where R is rotational joint, P is prismatic joint, U is universal joint, and S is spherical joint. Herein the fixed platform has a central point B and four kinematic joints B_i which are uniformly distributed at the vertex of the square. Similarly, the moving platform has a central joint A and four kinematic joints A_i which are also uniformly located at the vertex of the square. Moreover, its circumcircle radii are r_a and r_b, respectively. It should be noted that the complicated spherical joints in here are replaced by three revolute joints, whose axis are not collinear in space, are equivalent to a spherical joint. And more importantly, the compound spherical joint has larger rotational angle than that of integrated spherical joint. The parallel mechanism possesses one translation and two rotations degrees of freedom, so it can be used to a candidate orientation mechanism and connected two long tracks in series to achieve five-axis hybrid machine tool (as depicted in Fig. 1), which can complete the complex surface machining for engineering application.

Fig. 1.

A five-axis hybrid kinematic machine

Figure 2 shows the kinematic schematic of the parallel mechanism. A fixed coordinate system B-xyz with the z-axis being vertically the base is attached to the fixed platform, whose x-axis is along the vector BB₁, and y-axis is determined by the right hand rule. Similarly, the moving coordinate system A-uvw is attached on the moving platform and w-axis is vertical the moving platform. The u-axis is collinear with the vector AA₁, and the v axis is determined by the right hand rule.

Fig. 2.

Kinematic model of parallel manipulator

3 Kinematics Analysis

The moving platform can move along z direction and rotate around the x-axis and v-axis with consideration of mobility property. The homogeneous transformation matrix T of point A can be expressed as follows:

$$ {\mathbf{T}} = \left[ {\begin{array}{*{20}c} {\mathbf{R}} & {\mathbf{p}} \\ 0 & 1 \\ \end{array} } \right] = Rot(x,\alpha )Trans(z,d)Rot(v,\beta ) = \left[ {\begin{array}{*{20}c} {\cos \beta } & 0 & {\sin \beta } & x \\ {\sin \alpha \sin \beta } & {\cos \alpha } & { - \sin \alpha \cos \beta } & y \\ { - \sin \beta \cos \alpha } & {\sin \alpha } & {\cos \alpha \cos \beta } & z \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] $$

(1)

where p = [x, y, z]^T is the position coordinates of point A in the fixed coordinate system, $\alpha$ is the rotation angle around the x-axis, and $\beta$ is the rotation angle around the v-axis.

Additionally, once the rotation matrix R is obtained, then the rotational angels will be obtained

$$ \left\{ {\begin{array}{*{20}l} {\alpha = arc\tan 2({\mathbf{R}}(3,2),{\mathbf{R}}(2,2))} \hfill \\ {\beta = arc\tan 2({\mathbf{R}}(1,3),{\mathbf{R}}(1,1))} \hfill \\ \end{array} } \right. $$

(2)

where $R({\bullet},{\bullet})$ represents the row and column elements of the rotation matrix R.

Moreover, the aforementioned relations in (1) should also be summarized

$$ \left\{ {\begin{array}{*{20}l} {x = 0} \hfill \\ {y = - ds\alpha } \hfill \\ {z = ds\alpha } \hfill \\ \end{array} } \right. $$

(3)

where d is the movement distance along the z direction. So it is very easy to obtain the parasitic motion of the parallel mechanism

$$ y = - z\tan \alpha $$

(4)

Referring to Fig. 2, the closed vector constraint equation of i-the limb can be written as

$$ {\mathbf{b}}_{i} + d_{i} {\mathbf{s}}_{i} {\mathbf{ = p + a}}_{i} $$

(5)

where ${\mathbf{b}}_{i}$ is the position vector in the fixed coordinate system, and ${}^{A}{\mathbf{a}}_{i}$ is the position vector in the relative coordinate system, and ${\mathbf{a}}_{i}$ is the vector ${}^{A}{\mathbf{a}}_{i}$ in the fixed coordinate system, namely ${\mathbf{a}}_{i} = {\mathbf{R}} \cdot {}^{A}{\mathbf{a}}_{i}$.

The inverse kinematic solution of the parallel mechanism is determined as follows

$$ d_{i} = \left\| {{\mathbf{p + a}}_{i} - {\mathbf{b}}_{i} } \right\| $$

(6)

The unit vector of s_i can be obtained from (6)

$$ s_{i} = \left\| {{\mathbf{p + a}}_{i} - {\mathbf{b}}_{i} } \right\|/d_{i} $$

(7)

The velocity of the i-th active limb can be differentiated (5) with regard to time and written in matrix form

$$ \dot{d}_{i} = {\mathbf{J}}_{q} \left[ {\begin{array}{*{20}c} {v_{p} } \\ {w_{p} } \\ \end{array} } \right] $$

(8)

where ${\mathbf{v}}_{p}$ is the linear velocity and ${\varvec{\upomega}}_{p}$ is angular velocity of the mechanism, respectively.

In which ${\mathbf{J}}_{q} = \left[ {\begin{array}{*{20}l} {{\mathbf{s}}_{1}^{T} } \hfill & {[{\mathbf{a}}_{1} \times {\mathbf{s}}_{1} ]^{T} } \hfill \\ {{\mathbf{s}}_{2}^{T} } \hfill & {[{\mathbf{a}}_{2} \times {\mathbf{s}}_{2} ]^{T} } \hfill \\ {{\mathbf{s}}_{3}^{T} } \hfill & {[{\mathbf{a}}_{3} \times {\mathbf{s}}_{3} ]^{T} } \hfill \\ {{\mathbf{s}}_{4}^{T} } \hfill & {[{\mathbf{a}}_{4} \times {\mathbf{s}}_{4} ]^{T} } \hfill \\ \end{array} } \right]$

Additionally, the velocity of the moving platform can be also expressed by the independent variables ${{\dot{\mathbf{X}}}} = \left[ {\dot{\alpha }\quad \dot{\beta }\quad \dot{z}} \right]^{T}$

$$ {\mathbf{v}}_{p} = \left[ {\begin{array}{*{20}c} {\frac{\partial x}{\partial \alpha }} & {\frac{\partial x}{\partial \beta }} & {\frac{\partial x}{\partial z}} \\ {\frac{\partial y}{\partial \alpha }} & {\frac{\partial y}{\partial \beta }} & {\frac{\partial y}{\partial z}} \\ {\frac{\partial z}{\partial \alpha }} & {\frac{\partial z}{\partial \beta }} & {\frac{\partial z}{\partial z}} \\ \end{array} } \right] = {\mathbf{J}}_{vp} {{\dot{\mathbf{X}}}} $$

(9)

where ${\mathbf{J}}_{vp} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ { - z\sec^{2} \alpha } & 0 & { - \tan \alpha } \\ 0 & 0 & 1 \\ \end{array} } \right]$

The angular velocity of the moving platform can be expressed as a linear superposition of the Euler angles

$$ {\varvec{\upomega}}_{p} = Rot(\alpha )\dot{\alpha } + {\mathbf{0}}\dot{z} + Rot(\beta )\dot{\beta } = {\mathbf{J}}_{wp} {{\dot{\mathbf{X}}}} $$

(10)

where ${\mathbf{J}}_{wp} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {c\alpha } & 0 \\ 0 & {s\alpha } & 0 \\ \end{array} } \right]$

Therefore, the velocity mapping relationship between actuator joints variables and the independent parameter variables can be expressed as

$$ {{\dot{\mathbf{d}}}} = {\mathbf{J}}_{0} {{\dot{\mathbf{X}}}} = {\mathbf{J}}_{q} {\mathbf{J}}_{p} {{\dot{\mathbf{X}}}} $$

(11)

where ${\mathbf{J}}_{0}$ is the velocity Jacobian matrix of the parallel mechanism, and ${\mathbf{J}}_{p}$ is the Jacobian matrix of the moving platform, i.e. ${\mathbf{J}}_{p} = \left[ {\begin{array}{*{20}c} {{\mathbf{J}}_{vp} } \\ {{\mathbf{J}}_{wp} } \\ \end{array} } \right]$

By taking derivative of (11) with respect to time, the acceleration of the active limbs can de deduced as

$$ {{\ddot{\mathbf{d}}}} = {{\dot{\mathbf{J}}}}_{0} {{\dot{\mathbf{X}}}} + {\mathbf{J}}_{0} {{\ddot{\mathbf{X}}}} $$

(12)

Where

$$ {{\dot{\mathbf{J}}}}_{0} = \left[ {\begin{array}{*{20}l} {[{\mathbf{w}}_{1} \times {\mathbf{s}}_{1} ]^{T} } \hfill & {[({\mathbf{w}}_{p} \times {\mathbf{a}}_{1} ) \times {\mathbf{s}}_{1} + {\mathbf{a}}_{1} \times ({\mathbf{w}}_{1} \times {\mathbf{s}}_{1} )]^{T} } \hfill \\ {[{\mathbf{w}}_{2} \times {\mathbf{s}}_{2} ]^{T} } \hfill & {[({\mathbf{w}}_{p} \times {\mathbf{a}}_{2} ) \times {\mathbf{s}}_{2} + {\mathbf{a}}_{2} \times ({\mathbf{w}}_{2} \times {\mathbf{s}}_{2} )]^{T} } \hfill \\ {[{\mathbf{w}}_{3} \times {\mathbf{s}}_{3} ]^{T} } \hfill & {[({\mathbf{w}}_{p} \times {\mathbf{a}}_{3} ) \times {\mathbf{s}}_{3} + {\mathbf{a}}_{3} \times ({\mathbf{w}}_{3} \times {\mathbf{s}}_{3} )]^{T} } \hfill \\ {[{\mathbf{w}}_{4} \times {\mathbf{s}}_{4} ]^{T} } \hfill & {[({\mathbf{w}}_{p} \times {\mathbf{a}}_{4} ) \times {\mathbf{s}}_{4} + {\mathbf{a}}_{4} \times ({\mathbf{w}}_{4} \times {\mathbf{s}}_{4} )]^{T} } \hfill \\ \end{array} } \right] \cdot {\mathbf{J}}_{p} + {\mathbf{J}}_{q} \cdot \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ { - (\dot{z} \cdot \sec^{2} \alpha + \frac{2z \bullet \sin \alpha }{{\cos^{3} \alpha }} \bullet \dot{\alpha })} & 0 & {( - 1 - \tan^{2} \alpha ) \bullet \dot{\alpha }} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & { - \sin \alpha \bullet \dot{\alpha }} & 0 \\ 0 & {\cos \alpha \bullet \dot{\alpha }} & 0 \\ \end{array} } \right] $$

(12)

In which w_i is the angular velocity of the i-th limb defined in the fixed coordinate frame, and it can be expressed as.

$$ {\varvec{\upomega}}_{i} = \frac{{{\mathbf{s}}_{i} \times {\mathbf{v}}_{ai} }}{{d_{i} }} = {\mathbf{J}}_{wi} {{\dot{\mathbf{X}}}} $$

(13)

where the velocity ${\mathbf{v}}_{ai}$ of kinematic joints A_i connected to the moving platform can be obtained in the fixed coordinate system

$$ {\mathbf{v}}_{ai} = {\mathbf{v}}_{p} + {\varvec{\upomega}}_{p} \times {\mathbf{a}}_{i} = {\mathbf{J}}_{ai} \cdot {\mathbf{J}}_{p} \cdot {{\dot{\mathbf{X}}}} $$

(14)

and ${\mathbf{J}}_{ai} = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {a_{iz} } \hfill & { - a_{iy} } \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & { - a_{iz} } \hfill & 0 \hfill & {a_{ix} } \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & {a_{iy} } \hfill & { - a_{ix} } \hfill & 0 \hfill \\ \end{array} } \right]$, ${\mathbf{J}}_{wi} = \frac{{{\tilde{\mathbf{s}}}_{i} {\mathbf{J}}_{ai} {\mathbf{J}}_{p} }}{{d_{i} }}$

Suppose e₁ is the distance between the centroid B_i and the center of mass of lower sub-limb, while e₂ is the distance of the centroid A_i and the center of mass of upper sub-limb. The position vector of the centroid of the i-th limb with respect to the fixed coordinate system can be written as

$$ {\mathbf{r}}_{1i} = {\mathbf{b}}_{i} + e_{1} {\mathbf{s}}_{i} $$

(15)

$$ {\mathbf{r}}_{2i} = {\mathbf{b}}_{i} + (d_{i} - e_{2} ){\mathbf{s}}_{i} $$

(16)

Taking the derivative of (15) and (16) with respect to time, the velocity of the center can be obtained with respect to the fixed coordinate system.

$$ {\mathbf{v}}_{1i} = e_{1} {\varvec{\upomega}}_{i} \times {\mathbf{s}}_{i} = {\mathbf{J}}_{v1i} {{\dot{\mathbf{X}}}} $$

(17)

where ${\mathbf{J}}_{v1i} = - e_{1} \cdot {\tilde{\mathbf{s}}}_{i} {\mathbf{J}}_{wi}$

$$ {\mathbf{v}}_{2i} = (d_{i} - e_{2} ){\varvec{\upomega}}_{i} \times {\mathbf{s}}_{i} + \dot{d}_{i} \cdot {\mathbf{s}}_{i} = {\mathbf{J}}_{v2i} {{\dot{\mathbf{X}}}} $$

(18)

and ${\mathbf{J}}_{v2i} = (e_{2} - d_{i} ) \cdot {\tilde{\mathbf{s}}}_{i} {\mathbf{J}}_{wi} + {\mathbf{s}}_{i} {\mathbf{J}}_{di} {\mathbf{J}}_{p}$

Combining Eqs. (13), (17) and (18) yields

$$ {\mathbf{J}}_{v\omega 1i} = \left[ {\begin{array}{*{20}c} {{\mathbf{J}}_{v1i} } \\ {{\mathbf{J}}_{wi} } \\ \end{array} } \right],\quad {\mathbf{J}}_{v\omega 2i} = \left[ {\begin{array}{*{20}c} {{\mathbf{J}}_{v2i} } \\ {{\mathbf{J}}_{wi} } \\ \end{array} } \right] $$

(19)

where ${\mathbf{J}}_{v\omega 1i}$ and ${\mathbf{J}}_{v\omega 2i}$ are the Jacobian matrices of the i-th sub-limb.

Taking the derivative of (14) with respect to time, the acceleration of the point A_i can be obtained

$$ \dot{v}_{ai} = {{\dot{\mathbf{v}}}}_{p} + {{\dot{\varvec{\upomega}}}}_{p} \times {\mathbf{a}}_{i} + {\varvec{\upomega}}_{p} \times ({\varvec{\upomega}}_{p} \times {\mathbf{a}}_{i} ) $$

(20)

The angular acceleration velocity of the i-th sub-limb can be expressed as

$$ \dot{\omega }_{i} = \frac{{{\mathbf{s}}_{i} \times \dot{v}_{ai} - 2\dot{d}_{i} {\varvec{\upomega}}_{i} }}{{d_{i} }} = {\mathbf{J}}_{wi} {{\ddot{\mathbf{X}}}} + {{\dot{\mathbf{J}}}}_{wi} {{\dot{\mathbf{X}}}} $$

(21)

where ${{\dot{\mathbf{J}}}}_{wi} = \frac{{{\tilde{\mathbf{s}}}_{i} (({{\dot{\mathbf{J}}}}_{vp} - {\tilde{\mathbf{a}}}_{i} {{\dot{\mathbf{J}}}}_{wp} ) - [({\mathbf{J}}_{wp} {{\dot{\mathbf{X}}}}) \times ]{\tilde{\mathbf{a}}}_{i} {\mathbf{J}}_{wp} ) - 2{\mathbf{J}}_{di} {\mathbf{J}}_{0} {{\dot{\mathbf{X}}\mathbf{J}}}_{wi} }}{{d_{i} }}$

The acceleration of the center of mass of the i-th limb can be obtained by differentiating (17) and (18) with respect to time

$$ \dot{v}_{1i} = e_{1} {{\dot{\varvec{\upomega}}}}_{i} \times {\mathbf{s}}_{i} + e_{1} {\varvec{\upomega}}_{i} \times ({\varvec{\upomega}}_{i} \times {\mathbf{s}}_{i} ) = {\mathbf{J}}_{v1i} {{\ddot{\mathbf{X}}}} + {{\dot{\mathbf{J}}}}_{v1i} {{\dot{\mathbf{X}}}} $$

(22)

$$ \dot{v}_{2i} = \ddot{d}_{i} \cdot {\mathbf{s}}_{i} + 2\dot{d}_{i} ({\varvec{\upomega}}_{i} \times {\mathbf{s}}_{i} ) + (d_{i} - e_{2} ){{\dot{\varvec{\upomega}}}}_{i} \times {\mathbf{s}}_{i} + (d_{i} - e_{2} ){\varvec{\upomega}}_{i} \times ({\varvec{\upomega}}_{i} \times {\mathbf{s}}_{i} ) = {\mathbf{J}}_{v2i} {{\ddot{\mathbf{X}}}} + {{\dot{\mathbf{J}}}}_{v2i} {{\dot{\mathbf{X}}}} $$

(23)

where ${{\dot{\mathbf{J}}}}_{v1i} = - e_{1} {\tilde{\mathbf{s}}}_{i} {{\dot{\mathbf{J}}}}_{wi} - e_{1} {\mathbf{s}}_{i} \cdot ({\mathbf{J}}_{wi} {{\dot{\mathbf{X}}}})^{T} {\mathbf{J}}_{wi}$, ${{\dot{\mathbf{J}}}}_{v2i} = {\mathbf{s}}_{i} \cdot {{\dot{\mathbf{J}}}}_{0i} - 2{\mathbf{J}}_{0i} \cdot {{\dot{\mathbf{X}}}} \cdot {\tilde{\mathbf{s}}}_{i} \cdot {\mathbf{J}}_{wi} + (e_{2} - d_{i} )[{\tilde{\mathbf{s}}}_{i} \cdot {{\dot{\mathbf{J}}}}_{wi} + [({\mathbf{J}}_{wi} {{{\dot{\mathbf{X}}}}}) \times ]{\tilde{\mathbf{s}}} \cdot {\mathbf{J}}_{wi} ]$

So far, the velocity and acceleration of the moving platform and sub-limbs have been solved. In the next section, we will concentrate on the derivation of dynamics of the proposed mechanism.

4 Dynamics Analysis

In this section, the dynamic model of the parallel mechanism can be deduced by resorting to the principle of virtual work and d’Alembert’s formulation. Based on the previous work [13], just only the key points are presented, the following dynamic equation can be obtained

$$ {\mathbf{J}}_{0}^{T} {\varvec{\uptau}} + {\mathbf{J}}_{p} \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{e} + m_{a} {\mathbf{g}} - m_{a} {{\dot{\mathbf{v}}}}_{p} } \\ {{\mathbf{n}}_{e} - {}^{B}{\mathbf{I}}_{p} {{\dot{\varvec{\upomega}}}}_{p} - {\varvec{\upomega}}_{p} \times ({}^{B}{\mathbf{I}}_{p} {\varvec{\upomega}}_{p} )} \\ \end{array} } \right] + \sum\limits_{i} {{\mathbf{J}}_{v\omega 1i}^{T} \left[ {\begin{array}{*{20}c} {m_{1i} {\mathbf{g}} - m_{1i} {{\dot{\mathbf{v}}}}_{1i} } \\ { - {}^{B}{\mathbf{I}}_{1i} {{\dot{\varvec{\upomega}}}}_{i} - {\varvec{\upomega}}_{i} \times ({}^{B}{\mathbf{I}}_{1i} {\varvec{\upomega}}_{i} )} \\ \end{array} } \right] + \sum\limits_{i} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {\mathbf{g}} - m_{2i} {{\dot{\mathbf{v}}}}_{2i} } \\ { - {}^{B}{\mathbf{I}}_{2i} {{\dot{\varvec{\upomega}}}}_{i} - {\varvec{\upomega}}_{i} \times ({}^{B}{\mathbf{I}}_{2i} {\varvec{\upomega}}_{i} )} \\ \end{array} } \right]} } = 0 $$

(24)

By simplifying, the dynamics equation of the mechanism can be further deduced as

$$ {\varvec{\uptau}} = - \left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } \left( {{\mathbf{J}}_{p} \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{e} + m_{a} {\mathbf{g}} - m_{a} {{\dot{\mathbf{v}}}}_{p} } \\ {{\mathbf{n}}_{e} - {}^{B}{\mathbf{I}}_{p} {{\dot{\varvec{\upomega}}}}_{p} - {\varvec{\upomega}}_{p} \times ({}^{B}{\mathbf{I}}_{p} {\varvec{\upomega}}_{p} )} \\ \end{array} } \right] + \sum\limits_{i} {{\mathbf{J}}_{v\omega 1i}^{T} } \left[ {\begin{array}{*{20}c} {m_{1i} {\mathbf{g}} - m_{1i} {{\dot{\mathbf{v}}}}_{1i} } \\ { - {}^{B}{\mathbf{I}}_{1i} {{\dot{\varvec{\upomega}}}}_{i} - {\varvec{\upomega}}_{i} \times ({}^{B}{\mathbf{I}}_{1i} {\varvec{\upomega}}_{i} )} \\ \end{array} } \right] + \sum\limits_{i} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {\mathbf{g}} - m_{2i} {{\dot{\mathbf{v}}}}_{2i} } \\ { - {}^{B}{\mathbf{I}}_{2i} {{\dot{\varvec{\upomega}}}}_{i} - {\varvec{\upomega}}_{i} \times ({}^{B}{\mathbf{I}}_{2i} {\varvec{\upomega}}_{i} )} \\ \end{array} } \right]} } \right) $$

(25)

Equation (25) is a dynamics equation of the parallel mechanism, which can be simplified into the general form

$$ {\varvec{\uptau}} = {\mathbf{M}}({\mathbf{q}}){{\ddot{\mathbf{q}}}} + C({{\dot{\mathbf{q}}}},{\mathbf{q}}){{\dot{\mathbf{q}}}} + {\mathbf{N}} $$

(26)

with

$$ \begin{aligned} & {\mathbf{M}}({\mathbf{q}}) = \left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } \left\{ {{\mathbf{J}}_{p} \left[ {\begin{array}{*{20}c} {m_{a} {\mathbf{J}}_{vp} } \\ {{}^{B}{\mathbf{I}}_{p} {\mathbf{J}}_{wp} } \\ \end{array} } \right] + \sum\limits_{i}^{4} {{\mathbf{J}}_{v\omega 1i}^{T} \left[ {\begin{array}{*{20}c} {m_{1i} {\mathbf{J}}_{v1i} } \\ {{}^{B}{\mathbf{I}}_{1i} {\mathbf{J}}_{wi} } \\ \end{array} } \right]} } \right. + \left. {\sum\limits_{i}^{4} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {\mathbf{J}}_{v2i} } \\ {{}^{B}{\mathbf{I}}_{2i} {\mathbf{J}}_{wi} } \\ \end{array} } \right]} } \right\}{\mathbf{J}}_{0}^{ - 1} \\ & {\mathbf{C}}({{\dot{\mathbf{q}}}},{\mathbf{q}}) = \left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } \left\{ {{\mathbf{J}}_{p}^{T} \left[ {\begin{array}{*{20}c} {m_{a} {{\dot{\mathbf{J}}}}_{vp} } \\ {{}^{B}{\mathbf{I}}_{p} {{\dot{\mathbf{J}}}}_{wp} + [({\mathbf{J}}_{wp} {{{\dot{\mathbf{X}}}}}) \times ]({}^{B}{\mathbf{I}}_{p} {\mathbf{J}}_{wp} )} \\ \end{array} } \right]} \right. + \sum\limits_{i} {{\mathbf{J}}_{v\omega 1i}^{T} } \left. {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {m_{1i} {{\dot{\mathbf{J}}}}_{v1i} } \\ {{}^{B}{\mathbf{I}}_{1i} {{\dot{\mathbf{J}}}}_{wi} + [({\mathbf{J}}_{wi} {{{\dot{\mathbf{X}}}}}) \times ]({}^{B}{\mathbf{I}}_{1i} {\mathbf{J}}_{wi} )} \\ \end{array} } \right] + } \\ \end{array} \sum\limits_{i} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {{\dot{\mathbf{J}}}}_{v2i} } \\ {{}^{B}{\mathbf{I}}_{2i} {{\dot{\mathbf{J}}}}_{wi} + [({\mathbf{J}}_{wi} {{{\dot{\mathbf{X}}}}}) \times ]({}^{B}{\mathbf{I}}_{2i} {\mathbf{J}}_{wi} )} \\ \end{array} } \right]} } \right\}{\mathbf{J}}_{0}^{ - 1} \\ & - \,\left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } \left\{ {{\mathbf{J}}_{p}^{T} \left[ {\begin{array}{*{20}c} {m_{a} {\mathbf{J}}_{vp} } \\ {{}^{B}{\mathbf{I}}_{p} {\mathbf{J}}_{wp} } \\ \end{array} } \right] + \sum\limits_{i}^{4} {{\mathbf{J}}_{v\omega 1i}^{T} \left[ {\begin{array}{*{20}c} {m_{1i} {\mathbf{J}}_{v1i} } \\ {{}^{B}{\mathbf{I}}_{1i} {\mathbf{J}}_{wi} } \\ \end{array} } \right]} } \right. + \left. {\sum\limits_{i}^{4} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {\mathbf{J}}_{v2i} } \\ {{}^{B}{\mathbf{I}}_{2i} {\mathbf{J}}_{wi} } \\ \end{array} } \right]} } \right\}{\mathbf{J}}_{0}^{ - 1} {{\dot{\mathbf{J}}}}_{0} {\mathbf{J}}_{0}^{ - 1} \\ & {\mathbf{N}} = - \left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } \left\{ {\left. {{\mathbf{J}}_{p}^{T} \left[ {\begin{array}{*{20}c} {m_{a} {\mathbf{g}}} \\ {\mathbf{0}} \\ \end{array} } \right] + \sum\limits_{i} {{\mathbf{J}}_{v\omega 1i}^{T} \left[ {\begin{array}{*{20}c} {m_{1i} {\mathbf{g}}} \\ {\mathbf{0}} \\ \end{array} } \right]} + \sum\limits_{i} {{\mathbf{J}}_{v\omega 2i}^{T} \left[ {\begin{array}{*{20}c} {m_{2i} {\mathbf{g}}} \\ {\mathbf{0}} \\ \end{array} } \right]} } \right\}} \right. - \left[ {{\mathbf{J}}_{0}^{T} } \right]^{ + } {\mathbf{J}}_{p} \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{e} } \\ {{\mathbf{n}}_{e} } \\ \end{array} } \right] \\ \end{aligned} $$

where ${\mathbf{M}}({\mathbf{q}})$ is the inertia matrix, ${\mathbf{C}}({\mathbf{q}})$ is the concerning velocity (Centripetal force and Coriolis force), and ${\mathbf{N}}$ is the gravitational force and external generalized force term.

The elements of the inertia matrix M is dimensionally homogeneous, so one can employ the ratio of its minimum and maximum singular eigenvalue as the dynamic performance evaluation index

$$ k_{M} = \lambda_{{{\rm{min}} }} ({\mathbf{M}})/\lambda_{{{\rm{max}} }} ({\mathbf{M}}) $$

(27)

5 Simulation Examples

In order to verify the effectiveness of the kinematics and dynamics, the collaborative simulation analysis is adopted by the analysis tools, i.e. Simulink and Recurdyn. The simulation process can de described in Fig. 3.

Fig. 3.

Simulink and Recurdyn simulation flow block diagram

Specifically, the trajectory function of the moving platform is given as following

$$ \left\{ {\begin{array}{*{20}l} {\alpha = \frac{\pi }{30}\sin (\pi t)} \hfill \\ {\beta = \frac{\pi }{30}\cos (\pi t)} \hfill \\ {z = 0.7 + 0.05\sin (\pi t)} \hfill \\ \end{array} } \right. $$

(28)

After the simulation, the rotation matrix of the moving platform can be obtained. Calculated by the (2), the rotation angels $(\alpha ,\beta )$ of the moving platform can be required, which was compared with the desired trajectory and the illustrative results are depicted in Figs. 4 and 5 that verify the feasibility and accuracy of the parallel mechanism.

Fig. 4.

Trajectory comparison with $\alpha$ value

Fig. 5.

Trajectory comparison with $\beta$ value

Simultaneously, the positions, velocities, accelerations, and driving forces of the actuator joints can be drawn in Figs. 6, 7, 8 and 9. To facilitate analysis, just the velocity of the first and second actuators was presented, so did the acceleration of the third and fourth actuators.

Fig. 6.

Positions comparison with actuators

Fig. 7.

Velocities comparison with actuators

Fig. 8.

Accelerations comparison with actuators

Fig. 9.

Driving forces comparison with actuators

The positions, velocities, accelerations, and driving forces are varied smoothly in a certain range, and it demonstrates that the parallel mechanism has good performance characteristics of the kinematics and dynamics. Additionally, in kinematics, the analytical solutions are perfectly identical with simulation ones. But in dynamics simulation, there is a certain difference in driving force. It is due to omit the mass and velocity of the kinematic joints that affect the accuracy of calculation results.

The results simulated by the software Recurdyn were depicted in Fig. 10. On comparing the simulation and calculation results in Fig. 9, we find these results are satisfactory match, which demonstrate the analytic solutions are correct.

Fig. 10.

Driving forces of actuators with Recurdyn simulation

The analysis result of the dynamic dexterity is depicted in Fig. 11, where the distribution of dynamics dexterity at different heights is demonstrated. As illustrated in Fig. 11, the dynamic dexterity of the parallel mechanism is closer to 1, meaning that the parallel mechanism presents greater dynamics dexterity and higher acceleration performance within the workspace. Additionally, the distribution is uniform, the change is stable, and there is no sudden change, which illustrate that the proposed parallel manipulator has a potential application of the kinematic machine for good dynamics dexterity.

Fig. 11.

Dynamic dexterity of different height

6 Conclusions

In this paper, the major contributions of this paper are as follows: the kinematics analysis of the proposed parallel manipulator has been formulated, in terms of the principle of virtual work, the dynamics formulation of the proposed parallel manipulator is established and the inertia matrix including acceleration term is especially separated and the dynamic dexterity performance index is proposed. All the derived analytical solutions of the kinematics and dynamics are verified to be correct by employing Simulink and Recurdyn collaborative simulation, and provide a theoretical foundation for the intelligent control and calibration experiment in potential applications for the kinematic machine. A further extension of this work being investigated is intelligent control design and experimental calibration.