Vehicle Scheduling Optimization of Urban Distribution Considering Traffic Control

Abstract

In order to alleviate the internal traffic situation, the first- and second-tier cities have introduced traffic control measures to restrict the driving roads and period of freight vehicles, which makes the operation of distribution enterprises more difficult. Based on the recursive matrix of vehicle arrival time under soft time window, a distribution path optimization model considering urban freight vehicle traffic control is constructed, and a hybrid genetic algorithm based on “chain coding” and “sub-chain compensation” crossover operator is developed to solve the problem. The changing trend of total distribution cost under different control scenarios and the comparison of convergence quality under different sub-chain size thresholds show that the proposed model and algorithm are effective and practical.

1 Introduction

Urban distribution accelerates the circulation of local commodities, drives urban economic development, and improves the convenience of people’s lives. At the same time, it also brings external environmental problems such as environmental pollution, traffic congestion, and energy consumption. In response to this, various government departments have formulated corresponding to urban freight traffic control measures, hoping to limit the negative impact of distribution to people by limiting the driving time and road sections of freight vehicles within the city. The government’s management measures have had a major impact on distribution companies: enterprises must not only complete the distribution tasks with high efficiency and low cost, but also consider a series of practical factors such as prohibited road sections and restricted time limits.

Considering the distribution and optimization of urban freight vehicle traffic control is an extension of the vehicle routing problem (VRP), which is an NP-hard problem. Lang and Hu [1] used a hybrid genetic algorithm to solve the logistics distribution path optimization problem; Ombuki, et al. [2] combined Pareto method with genetic algorithm and verified the effectiveness of the algorithm through Solomon’s classical example. In terms of cargo control, George, et al. [3] established an evaluation model for freight policy to verify the effectiveness of cargo control policy implementation; Quak and Koster [4] applied the vehicle path calculation software Shortrec 7.0 to estimate the distribution route to analyze the cargo control policy, in order to analyze the influence of logistics decision-making on the operation cost and environment of distribution companies; Wang, et al. [5] assessed the current urban freight management policies and measures based on the investigation and analysis of the rules of freight transportation in the domestic commercial center area. Hu, et al. [6] conducted a comparative analysis of the comprehensive benefits of urban distribution optimization under different city freight traffic control scenarios, but did not consider the customer’s demand for delivery time windows. Huang [7] investigated in detail the traffic control policies of Beijing local licenses and foreign license vehicles, analyzed the logistics efficiency of various control policies, and proposed suggestions for improving the traffic control policies of Beijing freight vehicles. According to the influence of urban traffic restrictions and customer soft time window requirements on express delivery business, Liu, et al. [8] combined the traffic penalty cost and time penalty cost with the VRP problem, and proposed and verified the VRPTRSTW problem. In order to optimize the urban logistics distribution under the conditions of traffic control time, Zhe, et al. [9] comprehensively considers the distribution cost, environmental cost and delivery time of the distribution enterprise, and constructs a two-tier planning model.

In general, from the perspective of distribution enterprises, there are few studies that consider the problem of distribution optimization of urban freight traffic control policies.

Starting from the actual situation, based on the recursive matrix of vehicle arrival time under soft time window, this paper constructs a distribution route optimization model that considers the traffic control of urban freight vehicles, and develops a crossover operator based on “chain coding” and “sub-chain compensation”. The hybrid genetic algorithm is used to compare and analyze the distribution optimization schemes under different control scenarios with examples to provide the dispatching decision support for the optimization of distribution in the forbidden road sections and regulatory periods.

2 Problem Description and Modeling Conditions

Considering the distribution model of urban freight traffic control can be seen as an extension of the vehicle scheduling problem with time window constraints. Cargo delivery from multiple delivery vehicles to multiple demand points from one distribution center. Under the conditions positions, demand and time window constraints, weight per vehicle, and forbidden road sections, and the lower limit of the control period, we rationally arrange the route of the vehicle to minimize the total cost and meet the following assumptions:

• (1) The sum of demand for each distribution route does not exceed the carrying capacity of the vehicle.

• (2) The demand for each point can only be served once by one vehicle.

• (3) Each vehicle must start from the distribution center and return to it after completing the delivery.

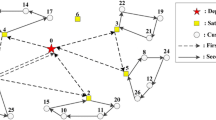
• (4) The forbidden roads are not accessible. Vehicles are only allowed to enter the restricted-period roads during the regulatory period (Fig. 1).

  Fig. 1

  

  The routing solution for VRPTW under traffic regulations

3 Scheduling Optimization Model and Algorithm of Urban Distribution Considering Traffic Control

3.1 Variables and Parameters

Delivery directed graph $G\,{ = }\,\left( {N,\,M} \right)$, the network characteristics are as follows: $m_{ij}$ represents the arc from the demand point $i$ to $j$; the set of all arcs is represented by $M$; the vertex $0$ represents the distribution center; the vertex $1,2,\, \ldots ,\,n$ represents the demand point; the vertex $0,1,2, \ldots \ldots ,n$ are recorded as a set $N$, $N = \left\{ {0,1,2, \ldots \ldots ,n} \right\}$; and the vertex $1,2, \ldots ,n$ are recorded as a set $C$, $C = \left\{ {1,2, \ldots \ldots ,n} \right\}$; $m_{ij}$ corresponds to the distance value $d_{ij}$ and the time value $t_{ij}$, which $t_{ij}$ is the running time from demand point $i$ to $j$; the demand point $i$ corresponds to the demand $q_{i}$, $s_{i}$ represents the service time; $V = \left\{ {1,2, \ldots ,k, \ldots ,K} \right\}$ is the vehicle collection, vehicle collection $k$ corresponds to vehicle maximum load capacity $Q_{k}$; $E$ represents prohibited road collections, there is $M \cap E = E$; in case of morning and evening peak limit,$[R_{b1} ,R_{e1} ]$ is the morning peak traffic control time, $[R_{b2} ,R_{e2} ]$ is the evening peak traffic control time, $R$ is a set of restricted roads that are subject to regulated time, with $M \cap R = R$, $R \cap E = \varnothing$. In addition, we usually use $\alpha$ to indicate the variable cost of the vehicle’s unit transport distance, $\beta$ is the fixed cost of the unit vehicle in the objective function. Here, $d_{ij}$, $t_{ij}$, $q_{i}$, $s_{i}$, $Q_{k}$, $R_{b}$, $R_{e}$, $\alpha$, $\beta$ are nonnegative, respectively.

In this model, there is decision variable $x_{ijk}$, for arcs $m_{ij}$ and vehicle $k$,

$$ x_{ijk} = \left\{ {\begin{array}{*{20}l} {1}, \hfill & {Vehicle\,k\,from\,customer\,i\,to\,customer\,j} \hfill \\ {0,} \hfill & {Otherwise} \hfill \\ \end{array} } \right. $$

The total number of customers visited by the vehicle $k$ is $n_{k}$, there is $n_{k} = \sum\limits_{i \in C} {\sum\limits_{j \in N} {x_{ijk} } }$. Collection $N_{k} = \left\{ {0,1,2, \ldots ,n_{k} } \right\}$; the number $l$ of the customer visited by vehicle $k$ is $O_{lk}$, $O_{lk} = \sum\limits_{j \in N} {jx_{{O_{(l - 1)k} jk}} }$; vehicle $k$ arrives at $l$th customer’s time is $TB_{lk}$, the leave time is $TE_{lk}$, there is $TE_{lk} = TB_{lk} + s_{{O_{lk} }}$, $TB_{lk}$ and $TE_{lk}$ are recursive sequence. The time at which the vehicle $k$ leaves the distribution center is denoted by $st_{k}$. When $m_{ij} \in R$, the expression for the time $TB_{1k}$ to reach the first customer is as follows:

$$ TB_{1k} = st_{k} + t_{{0O_{1k} }} + \left\{ {\begin{array}{*{20}l} 0 \hfill & {st_{k} < R_{b1} {\text{ or }}R_{e1} < st_{k} < R{\text{ or }}st_{k} > R_{e2} } \hfill \\ {R_{e1} - st_{k} } \hfill & {R_{b1} < st_{k} < R_{e1} } \hfill \\ {R_{e2} - st_{k} } \hfill & {R_{b2} < st_{k} < R_{e2} } \hfill \\ \end{array} } \right. $$

Then

$$ TB_{lk} = TE_{{\left( {l - 1} \right)k}} + t_{{O_{(l - 1)k} O_{lk} }} + \left\{ {\begin{array}{*{20}l} 0 \hfill & {TE_{{\left( {l - 1} \right)k}} \quad < R_{b1} {\text{ or }}R_{e1} < TE_{{\left( {l - 1} \right)k}} < R_{b2} {\text{ or }}TE_{{\left( {l - 1} \right)k}} > R_{e2} } \hfill \\ {R_{e1} - TE_{{\left( {l - 1} \right)k}} } \hfill & {R_{b1} < TE_{{\left( {l - 1} \right)k}} < R_{e1} } \hfill \\ {R_{e2} - TE_{{\left( {l - 1} \right)k}} } \hfill & {R_{b2} < TE_{{\left( {l - 1} \right)k}} < R_{e2} } \hfill \\ \end{array} } \right. $$

When $m_{ij} \notin R$, $TB_{lk} = TB_{(l - 1)k} + t_{{O_{(l - 1)k} O_{lk} }} + s_{{O_{(l - 1)k} }}$, this sequence establishes a one-to-one correspondence between variables $i$ and variables $\left( {l,\,k} \right)$, so $TB_{i} = TB_{lk}$. The demand point $i$ corresponds to the time window $\left[ {a_{i} ,\,b_{i} } \right]$, which $a_{i}$ represents the earliest delivery time allowed by $i$. And $b_{i}$ represents the latest delivery time. If the time $TB_{i}$ to arrive at the demand point $i$ is earlier than $a_{i}$ or later than $b_{i}$, the penalty should be cost, $p$, $q$ is the unit time penalty coefficient that the vehicle arrives early or late. The penalty cost function is expressed as follows:

$$ P_{i} (TB_{i} ) = \left\{ {\begin{array}{*{20}l} {p(a_{i} - TB_{i} )} \hfill & {TB_{i} < a_{i} } \hfill \\ 0 \hfill & {a_{i} \le TB_{i} \le b_{i} } \hfill \\ {q(TB_{i} - b_{i} )} \hfill & {b < TB_{i} } \hfill \\ \end{array} } \right. $$

3.2 Model Construction

$$ \hbox{min} \,z = \alpha \sum\limits_{k \in V}^{{}} {\sum\limits_{i \in N}^{{}} {\sum\limits_{j \in N}^{{}} {d_{ij} x_{ijk} } } } + \beta \sum\limits_{k \in V}^{{}} {\sum\limits_{j \in C}^{{}} {x_{0jk} } } + \sum\limits_{i \in C} {P_{i} (TB_{i} )} $$

(1)

$$ \text{s.t.}\quad \sum\limits_{{k{ \in }V}} {\sum\limits_{{j{ \in \mathsf{C}}}} {x_{ijk} } } = 1\quad \forall i \in N $$

(2)

$$ \sum\limits_{{i{ \in \mathsf{N}}}} {x_{ihk} - \sum\limits_{{j{ \in \mathsf{N}}}} {x_{hjk} = 0} } \quad \forall h \in C,\forall k \in V $$

(3)

$$ \sum\limits_{j \in C} {x_{0jk} = \sum\limits_{j \in C} {x_{j0k} } } \quad \forall k \in V $$

(4)

$$ \prod\limits_{{l \in N_{k} }}^{{}} {x_{{O_{lk} O_{(l + 1)k} k}} = \sum\limits_{j \in C} {x_{0jk} } } \,\forall k \in V $$

(5)

$$ \sum\limits_{k \in V} {x_{ijk} } = 0\quad \forall m_{ij} \in E $$

(6)

$$ \sum\limits_{k \in V} {x_{ijk} } = 0\quad \forall m_{ij} \in R $$

(7)

$$ \sum\limits_{{i{ \in }C}} {q_{i} } \sum\limits_{{j{ \in }N}} {x_{ijk} { \leqslant }Q_{k} } \quad \forall k \in V $$

(8)

$$ x_{ijk} \in \left\{ {0,1} \right\}\quad \forall i \in N,\forall j \in N,\forall k \in V $$

(9)

$$ TB_{i} \ge 0\quad \forall i \in N $$

(10)

The objective function (1) indicates that the total cost of distribution is minimal, including the vehicle distance cost, the number of vehicle activation costs, and the time delay or penalty cost ahead. Equation (2) indicates that each demand point can only be serviced once by a car; Eqs. (3) and (4) ensure that each vehicle starts from the distribution center and returns to the distribution center after completing a series of distribution tasks; Eq. (5) avoids the generation of sub-loops; Eq. (6) shows that no-forbidden roads are not traversable; Eq. (7) shows that restricted-route road sections are not traversable during the regulatory period; Eq. (8) shows the demand for each demand point on each path. The sum does not exceed the maximum load of the car; Eq. (9) is the integer constraint of the decision variable; Eq. (10) is the nonnegative constraint of the arrival time.

3.3 A Hybrid Genetic Algorithm Considering Urban Transport Control Constraints

Combining the structural characteristics of the feasible solution of the abovementioned optimization model and taking full account of the influence of traffic control-related constraints on genetic operators, a hybrid genetic algorithm based on “chain coding” was developed. The algorithm design mainly includes coding, generation of the initial population, determination of fitness function and design of genetic operator details as follows:

• (1) Coding

In the network diagram model, the delivery path for each freight car is embodied as a chain of $n_{k}$ distribution customers and $n_{k} + 1$ arcs. The information of the arcs can be derived from the point information in the distance (time) matrix. The encoding is set to a string of real numbers representing the order of delivery and the value is the number of the shipping customer. Several strings of real numbers form a chromosome. The length and quantity of the distribution chain are not fixed, the upper limit is $n$. Figure 2 (left) shows a distribution plan with three delivery routes, Fig. 2 (right) is its corresponding code.

Fig. 2

The corresponding between chromosome and feasible routes

• (2) Initial population

In order to ensure the randomness of the initial solution in the feasible domain, a heuristic rule for generating the initial population was designed. Let $A_{k}$ denotes the $k - th$ distribution chain, $A_{kw}$ denotes the $w - th$ customer that constitutes the chain, set customer collection $B\,{ = }\,C$ and collection $M_{w}$, and the latter denotes the reachable customers that start from $w - th$ customer (distribution center) in collection $B$ (including time limit line waiting for up to customers), set a variable $k\,{ = }\, 1$, the rules can be described as:

Step 1::

If $B{ = }{\varnothing }$, the rule ends, otherwise Step 2;

Step 2::

Select customer $i$ randomly in the set $M_{0}$ with probability $\left| {\frac{1}{{M_{0} }}} \right|$ and remove them from the set $B$. Let $w = 1$,$A_{kw} = i$; ➀ Customer $i$ is randomly selected with a probability of $\left| {\frac{1}{{M_{w} }}} \right|$ in the set $M_{w}$ and removed from the set $B$, let $w = w + 1$,$A_{kw} = i$,execute ➁; ➁ If $\sum\limits_{l = 1}^{w} {q_{{O_{lk} }} } > Q_{k}$, then a natural number $p$ from $1$ to $w - 1$ is generated with probability $\frac{1}{w - 1}$, and customer $A_{kw'} \left( {w^{{\prime }} = p + 1,p + 2, \ldots w.} \right)$ is added to set $B$, let $A_{{kw^{\prime}}} = 0\,(w^{{\prime }} = p + 1,p + 2, \ldots w.)$, $k = k + 1$, Perform Step 1; otherwise, execute (1); Vector $A_{k}$ is the delivery path and $k$ is the number of scheduled vehicles

• (3) Fitness function

Since the value of the objective function is the sum of the utility values, the difference between the merits and the weaknesses is not significant, so the fitness function selects the reciprocal of the objective function value, i.e., $f = 1/z$.

• (4) Select operator

Use a combination of best individual retention and roulette selection strategies.

• (5) Crossover operation

In order to overcome the influence of traffic route control and load constraints on the operator, in this paper, it simulates the block hypothesis principle and designs a “sub-chain compensation” crossover operator to decompose each distribution chain into “sub-chains” and perform other operations. It can be guaranteed that generating children are feasible solutions, thus avoiding the mode effect caused by the adjustment of solutions without theoretical support. Let parent individuals be $A$ and $B$, and the respective distribution chains are $A_{k}$ and $B_{k}$. The specific operation methods are:

➀ Set parameter $\varepsilon$ as the sub-chain size (length) threshold; ➁ Dissolve the distribution chain with a length greater than $\varepsilon$ in parent $A$. The decomposition step is to generate a random number $u$ from $1$ to $\varepsilon$, and decompose the sub-chain of length $u$ from $A_{k}$. Repeat this process until the remaining length of $A_{k}$ is less than $\varepsilon$, then can get $\delta$ sub-chains, from which to choose $\left[ {\frac{\delta }{2}} \right]$ sub-chains to compose set $SA$; ➂ In every distribution chain $B_{k}$ of parent $B$, the customers contained in $SA$ are eliminated and several sub-chains are obtained. The sub-chain whose size exceeds $\alpha$ is decomposed by applying the method in ➁ to obtain sub-chain set $SB$; ➃ Combining $SA$ and $SB$ into $CB$, which contains the customer at both ends of the sub-chain constitute a set $CC$, and the construction of a new individual rule is as follows:

Let $C_{k}$ denote the $k - th$ distribution chain of the child, $C_{kw}$ denotes the $w - th$ chain that constitutes the chain, and let $M_{w}$ denote the reachable customer (including time limit line) in the set $CC$ starting from the end customer (distribution center) of the $w - th$ child chain. Let us set the variable $k = 1$. The rule can be described as:

Step 1::

If $CB = \varnothing$, the rule ends; Otherwise Step 2;

Step 2::

In the set $M_{0}$, the customer $i$ in $CC$ and its sub-chain $I$ are randomly selected with probability $\left| {\frac{1}{{M_{0} }}} \right|$, $I$ is removed from $CB$, and the endpoints $i$ and $i'$ of $I$ are removed from $CC$. Let $w = 1$, $C_{kw} = I$;

➀ In the set $M_{w}$, the customer $i$ in $CC$ and its sub-chain $I$ are randomly selected with probability $\left| {\frac{1}{{M_{w} }}} \right|$, $I$ is removed from $CB$, and the endpoints $i$ and $i'$ of $I$ are removed from $CC$. Let $w = w + 1$, $C_{kw} = I$, execute ➁; ➁ If $C_{k}$ breaks the load-carrying constraint, a natural number $p$ from $1$ to $w - 1$ is generated with probability $\frac{1}{w - 1}$, and the child chain $C_{{kw^{\prime}}} (w^{\prime} = p + 1,p + 2, \ldots w.)$. Join $CB$, the endpoint joins $CC$ and let $C_{{kw^{\prime}}} = 0(w^{\prime} = p + 1,p + 2, \ldots w.)$, $k = k + 1$, Perform Step 1; otherwise, execute ➀; The vector $C_{k}$ is the delivery path and $k$ is the number of scheduled vehicles.

• (6) Variation operation.

Select individual $G$ with mutation probability $P_{m}$. The steps for mutation are:

Step 1::

Customer $i$ and customer $j$ are randomly selected on the chromosome, and a new chromosome $G^{{\prime }}$ is formed at the exchange position. If $G^{{\prime }}$ is an infeasible solution (it does not meet the prohibited road segment constraint), it is discarded, Step 1 is performed, otherwise Step 2 is performed;

Step 2::

Compare the fitness function values of $G$ and $G^{{\prime }}$, if $f(G)> f(G^{{\prime }} )$, then execute Step 1, otherwise accept $G^{{\prime }}$, the mutation ends

4 Numerical Experiments and Result Analysis

The numerical experiment is designed to compare the experimental examples under different control scenarios. Benchmark Problems is a VRPTW standard test question bank designed by Solomon in 1953. This article selects C109 and R209, which are more suitable for real-time scenarios, as the example data. Randomly select 10, 20, and 30% of the inter-customer routes as forbidden road sections. Rules for selecting routes under regulation period: Select customer points randomly, 20% of the inter-customer path within the radial $r$, the radius of this point is the restricted road section.

Experiment 1::

The regulatory period is the morning peak 7:00–9:00 pm peak 17:00–19:00, and the calculation results of the case C109 and R209 corresponding to different forbidden road sections are shown in Table 1.

Experiment 2::

Select 20% of forbidden road sections. Table 2 shows the calculation results of calculation cases C109 and R209 corresponding to different regulatory periods

From the calculation results, it can be seen that the forbidden road section has a greater influence on the total cost of distribution than the control period. With the increase of the scope of control, the total cost of distribution of case C109 is larger than that of case R209, which is almost an exponential increase. This shows that the relatively uniform distribution of customer aggregation is more sensitive to the regulatory policy. In order to cope with urban freight traffic control, distribution companies should develop a route optimization plan in conjunction with the distribution of customer points. When customers tend to aggregate and distribute, they can establish regional distribution centers or negotiate to change delivery time windows (Table 3).

Table 1 Comparison of calculation results for different number of forbidden road sections for examples C109 and R209

Table 2 Computation results of calculation examples C109 and R209 corresponding to different regulatory periods

Table 3 Basic experimental data

5 Conclusions and Outlook

By establishing a distribution optimization model that takes into account the traffic control of urban freight vehicles, a hybrid genetic algorithm based on “chain coding” and “sub-chain compensation” crossover operators is developed to calculate numerical experiments. The results show that different control policies apply to distribution plans. The policy of forbidden road sections has a greater impact on distribution companies than the control period, and the calculation of customer aggregation is faster than the even distribution of total cost. Distribution companies can use this model and algorithm to calculate the optimal distribution route that takes into account the traffic control of vehicles.

Further research can quantify the advantages and disadvantages of traffic control policies for vehicles from perspectives such as the opportunity cost of distribution companies and the social responsibility of distribution companies.