Uncertainty Modeling for Nonlinear Dynamic Systems––Loadings Applied in Time Domain

Abstract

Enormous amount of damages to structures caused by recent major seismic events indicate shortcomings or incompleteness in their design. Some of the major weaknesses in current practices include the inability to incorporate major sources of uncertainty in the formulation, realistic structural behavior leading to failure, and most importantly predicting the exact design earthquake time history expected during the lifetime of a structure for a specific site. To address excessive economic losses, the performance-based seismic design (PBSD) concept is being advocated in the U.S., particularly for steel structures. This is essentially an advanced risk-based design concept. The author’ steam proposed several novel concepts to estimate the underlying risk considering major sources of nonlinearity and uncertainty in the past, including the stochastic finite element concept. However, the risk analysis procedure for realistic nonlinear structural systems excited by seismic loadings in the time domain, required for the most sophisticated deterministic analysis, is not available at present. To make the design more seismic load tolerant, multiple earthquake time histories need to be considered to incorporate uncertainty in the frequency content. If one decides to use simulations to extract the reliability information, it may not be possible; it may require several years of continuous running of a computer. The author’s team proposed several alternatives to simulations. Several related topics to make structures more seismic damage tolerant are presented in this paper.

1 Introduction

The scope, contents, size, and levels of participations of the Fourth International Conference on Reliability, Safety, and Hazard (ICRESH-2019) clearly indicate that maturity of the risk and reliability areas. It has become multidisciplinary. Although the developments of the related areas are relatively new, the acceptance of the risk-based basic concept by the world communities is extremely noteworthy [1,2,3,4,5]. Reliability, Safety, and Hazard (RSH) has become the building block for all most all design guidelines, particularly for the civil engineering applications. It has become an integral part of engineering education, for both undergraduate and graduate levels, at least in the U.S. In fact, all undergraduate students must take a required course on the topic before graduation as recommended by the Accreditation Board of Engineering and Technology (ABET).

As expected, numerous scholars contributed to the development of RSH. The developments of the related areas will be briefly summarized in the following sections. However, risk analysis procedure for realistic nonlinear structural systems excited by seismic loadings applied in the time domain, required for the most sophisticated deterministic analysis, is not available at present. It is a major knowledge gap in the reliability estimation procedures. To make a particular design more seismic load tolerant, multiple earthquake time histories need to be considered to incorporate uncertainty in the frequency content. If one decides to use simulations to extract the reliability information, it may not be possible; it may require several years of continuous running of a computer, as will be discussed during the presentation. The author and his team members proposed several alternatives to extract the information [6,7,8,9,10,11,12,13,14]. This is the subject of this paper.

2 Background Information

Risk or safety is always estimated with respect to a desired or required performance level. This is commonly known as the limit state function (LSF) in the literature. It is essentially a function of all resistance and load-related random variables and the design or performance requirement or criterion. An LSF can be related to the strength or serviceability. An LSF also can be explicit or implicit in nature. If it is explicit, its partial derivatives with respect to all the random variables with be available, and the commonly used first-order reliability method (FORM) or the second-order reliability method (SORM) can be used to extract the reliability information. Unfortunately, LSFs are expected to be implicit for realistic civil engineering structures. For an example, the lateral displacement at the top of a large structural system may not be expressed in terms of all the resistance and load-related random variables. If major sources of nonlinearity need to be appropriately incorporated in the formulation, it will make an LSF implicit. For dynamic loadings, LSFs are also expected to be implicit. One of the major complains of the deterministic community who do not appreciate reliability-based design is that it cannot incorporate the realistic loading conditions and the corresponding structural behavior. The most sophisticated deterministic response evaluation of structures requires that the seismic loading is applied in time domain considering major sources of nonlinearity. For this class of problems, the LSFs are implicit and the commonly used FORM/SORM based methods cannot be used for the reliability estimation.

The author, in the very early stage of his academic career, realized that to make reliability-based design acceptable to the deterministic community, it is necessary to follow all the procedures followed by them, however, they must incorporate all major sources of uncertainty in the design variables. He concluded that the finite element method (FEM)-based analysis is a very powerful tool used in many engineering disciplines to analyze structures. Representing a complicated large structural system by finite elements, it is relatively easy and straightforward to consider complicated geometric arrangements and constitutive relationships of material used, realistic connection and support conditions, various sources of nonlinearity, and the load path to failure. It gives very reasonable results for a set of assumed values of the variables but unable to incorporate information on uncertainty in them. As mentioned earlier, the basic weakness of most reliability-based methods is that they failed to incorporate realistic structural behavior. This prompted the author to combine the desirable features of the two concepts, leading to the development of the stochastic finite element method (SFEM) concept. It is essentially a FORM-based reliability estimation procedure for structures represented by finite elements.

The basic concept can be described as follows. Without losing any generality, the LSF can be expressed as $g({\mathbf{x}},{\mathbf{u}},{\mathbf{s}}) = 0$, where x is a set of basic random variables, u is the set of displacements and s is the set of load effects (except the displacements, such as internal forces). The displacement ${\mathbf{u}} = {\mathbf{QD}}$, where D is the global displacement vector and Q is a transformation matrix. For reliability computation using FORM, it is convenient to transform x into the standard normal space ${\mathbf{y}} = {{y}}({\mathbf{x}})$ such that the elements of y are statistically independent and have a standard normal distribution. An iteration algorithm can be used to locate the design point (the most likely failure point) on the limit state function using the first-order approximation. The structural response and the response gradient vectors are calculated using FEMs at each iteration. The following iteration scheme can be used for finding the coordinates of the design point:

$$ {\mathbf{y}}_{i + 1} = \left[ {{\mathbf{y}}_{i}^{t} \alpha_{i} + \frac{{g\left( {{\mathbf{y}}_{i} } \right)}}{{\left| {\nabla g\left( {{\mathbf{y}}_{i} } \right)} \right|}}} \right]\alpha_{i} $$

(1)

where

$$ \nabla g\left( {\mathbf{y}} \right) = \left[ {\frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial y_{1} }}, \cdots ,\frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial y_{n} }}} \right]^{t} \,{\text{and}}\,\alpha_{i} = - \frac{{\nabla g\left( {{\mathbf{y}}_{i} } \right)}}{{\left| {\nabla g\left( {{\mathbf{y}}_{i} } \right)} \right|}} $$

(2)

To implement the algorithm, the gradient $\nabla g\left( {\mathbf{y}} \right)$ of the limit state function in the standard normal space can be derived as [5]:

$$ \nabla g\left( {\mathbf{y}} \right) = \left[ {\begin{array}{*{20}l} {\frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial {\mathbf{s}}}}{\mathbf{J}}_{s,x} + } \hfill \\ {\left( {{\mathbf{Q}}\frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial {\mathbf{u}}}} + \frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial {\mathbf{s}}}}{\mathbf{J}}_{s,D} } \right){\mathbf{J}}_{D,x} + } \hfill \\ {\frac{{\partial g\left( {\mathbf{y}} \right)}}{{\partial {\mathbf{x}}}}} \hfill \\ \end{array} } \right]{\mathbf{J}}_{y,x}^{ - 1} $$

(3)

where ${\mathbf{J}}_{i,j}$’s are the Jacobians of transformation (e.g., ${\mathbf{J}}_{s,x} = \partial {\mathbf{s}}/\partial {\mathbf{x}}$), and y_i′s are statistically independent random variables, as discussed earlier. The evaluation of the quantities in Eq. (3) will depend on the problem under consideration (linear or nonlinear, two- or three-dimensional, etc.) and the performance functions used. The essential numerical aspect of SFEM is the evaluation of three partial derivatives, $\partial g/\partial {\mathbf{s}}$, $\partial g/\partial {\mathbf{u}}$, and $\partial g/\partial {\mathbf{x}}$, and four Jacobians, ${\mathbf{J}}_{s,x}$, ${\mathbf{J}}_{s,D}$, ${\mathbf{J}}_{D,x}$, and ${\mathbf{J}}_{y,x}$. They can be evaluated by procedures suggested in [5]). Once the coordinates of the design point ${\mathbf{y}}^{*}$ are evaluated with a preselected convergence criterion, the reliability index β can be evaluated as

$$ \beta = \sqrt {({\mathbf{y}}^{ *} )^{t} ({\mathbf{y}}^{ *} )} $$

(4)

The evaluation of Eq. (4) will depend on the problem under consideration and the limit state functions used. The probability of failure, P_f can be calculated as

$$ {P_{f}} =\Phi \left( { - \beta } \right) = 1.0 -\Phi \left( \beta \right) $$

(5)

where $\Phi$ is the standard normal cumulative distribution function. Equation (5) can be considered as a notational failure probability. It indicates that the reliability index is larger, the probability of failure will be smaller.

3 Challenges in Implementation of the SFEM-Based Reliability Evaluation Concept

The development of the SFEM-based reliability evaluation was very exciting in the early 80s. When a book was published on the topic, it generated a lot of interest and widely referred even at present. However, the major objection of the readers is that that they did not have access to the computer programs developed by the author with the help of about a dozen doctoral students. At present, it may be impractical to rewrite the programs considering various advanced computational platforms currently available. For wider applications and addressing the computational needs, the basic SFEM concept may need to be improved.

In general, the nonlinear response estimations of realistic dynamic structures by applying the excitation in the time domain can be very time consuming and cumbersome. These challenges also make the reliability evaluation using the SFEM concept inappropriate or challenging. One logical alternative will be the use of the basic simulation. However, one deterministic analysis of structures for practical application excited by dynamic loadings applied in time domain may require about 1 h of computer time. For 10,000 simulations (very small for low probability events), it will require about 10,000 h or about 1.14 years of continuous running of a computer. Thus, the basic simulation is not an acceptable alternative. An alternative to simulation is required. To incorporate the uncertainty information in the dynamic formulation, the classical random vibration concept can be used. However, it may not be possible to apply the dynamic loadings in the time domain; they are generally expressed in terms of power spectral density functions. Thus, the major sources of nonlinearity may not be appropriately incorporated in the formulation, as expected by the deterministic community.

The above discussions clearly indicate that a new reliability evaluation technique is necessary for dynamic systems excited by dynamic loadings, including seismic loading, in the time domain. The procedure is expected to provide an alternative to the classical random vibration approach and the basic simulation approach.

4 A Novel Reliability Approach for Nonlinear Dynamic Systems––Loads Applied in Time Domain

As expected, the LSFs for this class of problem are expected to be implicit in nature. The response surface (RS) concept can be used to express an implicit LSF explicitly even in an approximate way. An RS can be expressed in the form of a linear or polynomial function. It is generally formulated by deterministically estimating responses by following specified schemes and then fitting a polynomial through all the generated response data in terms of all the design variables in an approximate way. It is generally expressed as a linear or quadratic polynomial and needs to be developed in the failure region. Obviously, the total number of deterministic evaluations required to formulate an RS is an important consideration. The success of this approach depends on many factors as will be discussed later.

The basic response surface concept (RSC) has not been widely used for structural reliability estimation for several major reasons including it neglects the distribution information of random variables (RVs), it is extremely difficult to predict the failure region for realistic structural systems, and the optimum number of deterministic evaluations needed to generate an acceptable polynomial. In developing the new concept, the author and his team decided to integrate RSC with FORM to bring distributional information of RVs in the formulation and to efficiently locate the failure region. This can be achieved by the SFEM concept discussed earlier by representing structures with FEs and capturing their realistic linear and nonlinear behavior as they go through various phases before failure, as is commonly practiced by the deterministic community. The integration will eliminate the first two deficiencies. The removal of the deficiency related to the optimum number of deterministic evaluations will be discussed later. An RS generated with this integrated approach will be significantly different than what is reported in the literature [15,16,17]. To document the different characteristics, it will be denoted hereafter in this paper as the significantly modified RS or simply (SMRS).

To maintain the computational efficiency and considering that a linear SMRS will be inadequate to represent an RS for the class of dynamic problems of interest, second-order polynomial, without and with cross terms becomes very attractive. The polynomial can be represented as

$$ {\hat{\text{g}}}\left( {\mathbf{X}} \right) = b_{0} + \mathop \sum \limits_{i = 1}^{k} b_{i} X_{i} + \mathop \sum \limits_{i = 1}^{k} b_{ii} X_{i}^{2} $$

(6)

$$ {\hat{\text{g}}}\left( {\mathbf{X}} \right) = b_{0} + \mathop \sum \limits_{i = 1}^{k} b_{i} X_{i} + \mathop \sum \limits_{i = 1}^{k} b_{ii} X_{i}^{2} + \mathop \sum \limits_{i = 1}^{k - 1} \mathop \sum \limits_{j > i}^{k} b_{ij} X_{i} X_{j} $$

(7)

where $X_{i} (i = 1,2, \ldots ,k)$ is the ith RV, and b₀, b_i, b_ii, and b_ij are unknown coefficients to be determined, and k is the number of RVs in the formulation. These coefficients need to be estimated by conducting multiple deterministic analyses following the basic RS concept.

In satisfying the concept of RS, the location of the center points around which sampling points will be selected and experimental schemes that can be used in selecting sampling points need to be finalized at this stage. Since FORM is an integral part of generating SMRS, the team decided to initiate the iterations at the mean values of all RVs, giving the initial location of the center point and converting all of them in the standard normal variable space. The location of the center point is expected to converge to the most probable failure point after a few iterations. Sampling schemes used for most engineering applications are saturated design (SD) and central composite design (CCD) [15]. SD is less accurate but more efficient since it requires only as many sampling points as the total number of unknown coefficients to define an SMRS. SD without cross terms consists of one center point and 2 k axial points. Therefore, a second-order RS can be generated using 2 k + 1 FE analyses. SD with cross terms consists of one center point, 2 k axial points, and $k\left( {k - 1} \right)/2$ edge points [18]. It will require $\left( {k + 1} \right)\left( {k + 2} \right)/2$ FE analyses. CCD [19] consists of a center point, two axial points on the axis of each RV at distance $h = \sqrt[4]{{2^{k} }}$ from the center point, and $2^{k}$ factorial design points. It will require a total of $2^{k} + 2k + 1$ FE analyses to generate a second-order SMRS. CCD is more accurate but less efficient: it requires the second-order polynomial with cross terms and regression analysis is used to generate the function requiring many sampling points.

The above discussions clearly indicate that the proposed procedure is iterative in nature. Considering both accuracy and efficiency, and after considerable deliberations, the team decided to use SD in the intermediate iterations and CCD in the final iteration. At this time, it is important to consider the number of deterministic finite element analyses (DFEA) required to generate an SMRS. Generating an SMRS using SD without cross terms and CCD with cross terms will require 2 k + 1 and $2^{k} + 2k + 1$ DFEA, respectively, where k is the total number of RVs in the formulation. For the relatively small value of k, say k = 5, it will require 11 and 43 DFEA, respectively. However, if k = 50, it will require 101 and 1.126 × 10¹⁵ DFEA, respectively. This discussion clearly indicates that despite its numerous advantages, CCD in its basic form cannot be used for the reliability analysis of large structural systems.

The discussion also points out the important role of k in the proposed algorithm and its implementation potential. The total number of RVs in the formulation needs to be reduced at the earliest possible time. It is well known to the profession that the propagation of uncertainty from the parameter to the system level is not equal for all the RVs in the formulation. Haldar and Mahadevan (2000a) suggested that the information on the sensitivity index, the information will be readily available from the FORM analyses, can be used for this reduction purpose. RVs with relatively small sensitivity indexes can be considered as deterministic at their respective mean values without significantly sacrificing accuracy of the algorithm. Denoting the reduced number of RVs as k_R, the total number of RVs will be reduced from k to k_R in all equations developed so far. The implementation potential of CCD improves significantly with this reduction.

Based on the experience gained in dealing with SFEM [8, 20,21,22,23], the author believes that the computational efficiency in generating an SMRS will be significantly improved but still will require thousands of FE analyses requiring months of continuous running of a computer. This will not satisfy the major objective of the team. More improvements are necessary.

The final iteration of the proposed procedure uses CCD; it consists of one center point, 2k_R axial points, and $2^{{k_{R} }}$ factorial points. To improve the efficiency further, the cross terms and the necessary sampling points are considered only for the most significant RVs in sequence in order of their sensitivity indexes until the reliability index converges with a predetermined tolerance level. This may cause ill-conditioning of the regression analysis due to the lack of data. To prevent ill-conditioning, just the cross terms for m most significant variables are considered in the polynomial expression. With this improvement, DFEA required to extract the reliability information using the proposed procedure and this improvement will be required $2^{{k_{R} }} + 2k_{R} + 1$ and $2^{m} + 2k_{R} + 1$, respectively.

5 Moving Least Squares and Kriging Methods

At this stage, hundreds of response data generated by conducting nonlinear FE analyses by applying the dynamic loading in the time domain will be available. To generate SMRS using CCD in the final iteration, it is necessary to fit a polynomial through them. The team investigated moving least squares and Kriging methods for this purpose.

For regression analysis, the least squares method (LSM) is generally used. LSM is essentially a global approximation technique in which all the sample points are assigned with the equal weight factor. The team believes the weight factors should decay as the distances between the sampling points and the SMRS increase. Incorporation of this concept leads to moving LSM or MLSM. Thus, in MLSM, an SMRS is generated using the generalized least squares technique with different weights factors for the different sampling points [24,25,26,27,28,29].

MLSM is a significant improvement, however, since it is based on regression analysis, the generated SMRS will be in an average sense. This weakness needs to be improved. The team investigated the use of a surrogate meta model like Kriging to generate an appropriate SMRS, which will pass through all sample points. Kriging predictor technique is essentially the best linear unbiased predictor approximation of SMRS and its gradients can be used to extract information on unobserved points. One of the major desirable features of Kriging important to the present study is that it provides information on spatially correlated data. Several Kriging models are reported in the literature [30, 31]. The team decided to use Universal Kriging since it is capable of incorporating external drift functions as supplementary variables [32]. It is discussed very briefly below.

Denoting ${\hat{\text{g}}}\left( {\mathbf{X}} \right)$ to represent an SMRS, the concept can be expressed as

$$ {\hat{\text{g}}}\left( {\mathbf{X}} \right) = \mathop \sum \limits_{i = 1}^{r} \omega_{i} Z\left( {{\mathbf{X}}_{i} } \right) $$

(8)

where $\omega_{i} \in R,i = 1,2,..,r$ are unknown weights corresponding to the observation vector ${\mathbf{Z}} \equiv \left[ {Z\left( {{\mathbf{X}}_{i} } \right),i = 1,2, \ldots ,r} \right]$ which is estimated by performing r deterministic FE analyses. The observation vector Z contains the response of the system at the experimental sampling points.

The Gaussian process $Z\left( {\mathbf{X}} \right)$ is assumed to be a linear combination of a nonstationary deterministic drift function $u\left( {\mathbf{X}} \right)$ and a residual random function $Y\left( {\mathbf{X}} \right)$. It can be mathematically presented as [33, 34].

$$ Z\left( {\mathbf{X}} \right) = u\left( {\mathbf{X}} \right) + Y\left( {\mathbf{X}} \right) $$

(9)

where $u\left( {\mathbf{X}} \right)$ is a second-order polynomial with cross terms and $Y\left( {\mathbf{X}} \right)$ is an intrinsically stationary function with zero mean with underlying variogram function $\gamma_{\text{Y}}$. The relationship can be developed by the variogram function. The variogram function can be generated by assuming that the difference between responses at two sample points only depends on their relative locations. Using the dissimilarities with the same distance in the variogram cloud, the experimental variogram can be generated. The dissimilarity function can be represented as

$$ \gamma^{*} \left( {l_{i} } \right) = \frac{1}{2}\left[ {Z\left( {x_{i} + l_{i} } \right) - Z\left( {x_{i} } \right)} \right]^{2} $$

(10)

where $\gamma^{*} \left( {l_{i} } \right)$ is the dissimilarity function for the ith RV separated by a distance $l_{i}$, and $x_{i}$ is the coordinate of the sample point in the ith RV axis. Since dissimilarity function is symmetric with respect to $l_{i}$, it will be considered only for the absolute value of $l_{i}$. The variogram cloud is the graphical representation of the dissimilarity function as a function of $l_{i}$. Experimental variogram can be considered as the average of the dissimilarities with the same distance $l_{i}$.

Several parametric variogram functions including Nugget effect, Exponential, Spherical, and Bounded linear models are reported in the literature. Least square and weighted least square regression are generally used for fitting these models to the experimental variogram. The family of stable anisotropic variogram models can be represented as [31]

$$ \gamma_{Y} \left( {\mathbf{l}} \right) = b\left\{ {1 - { \exp }\left[ {\mathop \sum \limits_{i = 1}^{k} - \frac{{\left| {l_{i} } \right|^{q} }}{{a_{i} }}} \right]} \right\}{\text{with}}\,0 < q < 2 $$

(11)

where l is a vector of $l_{i}$ components, a_i and b are the unknown coefficients to be determined, and k is the number of RVs. These models asymptotically approach to b, commonly known as sill parameter. Parameter a_i, called the range parameter, represents ith orthogonal direction range at which the variogram $\gamma_{Y} \left( {\mathbf{l}} \right)$ almost passes through the 95% of the sill value. Since Eq. (8) with q = 2 is unrealistic, it is not considered in this study. Variograms are generated using all the models and the model with the highest coefficient of determination [4] is selected to generate an SMRS using Eq. (8).

In estimating weight factors $\omega_{i}$ in Eq. (8), uniform unbiasedness can be assured satisfying the universality conditions as [34]

$$ \mathop \sum \limits_{i = 1}^{r} \omega_{i} f_{p} \left( {{\mathbf{X}}_{i} } \right) = f_{p} \left( {{\mathbf{X}}_{0} } \right)\,{\text{for}}\,p = 0,1, \ldots ,P $$

(12)

where $f_{p} \left( {{\mathbf{X}}_{i} } \right)$ is the ordinary regression function of a second-order polynomial with cross terms, ${\mathbf{X}}_{i}$ is the coordinates of the ith sampling point, and ${\mathbf{X}}_{0}$ is the coordinates of the unsampled point in which the response of the structure needs to be predicted. For each regressor variable ${\mathbf{X}}_{i}$, r sets of data are collected, and each set consists of P observations [4]. The weight factors can be obtained by minimizing the variance of the prediction error using the Lagrange multipliers and the optimality criteria as

$$ \left( {\begin{array}{*{20}c} {\varvec{\upomega}} \\ {\varvec{\uplambda}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\varvec{\Gamma}}_{Y} } & {\mathbf{F}} \\ {{\mathbf{F}}^{T} } & 0 \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {{\varvec{\upgamma}}_{Y,0} } \\ {{\mathbf{f}}_{0} } \\ \end{array} } \right) $$

(13)

Assuming F is a full column rank matrix, i.e., all columns are linearly independent, Wackernagel [31] showed that Eq. (13) will give a unique solution. For computational efficiency and to avoid inverting Eq. (13), the closed-form solution for the unknown weights can be derived as

$$ {\varvec{\upomega}} = {\varvec{\Gamma}}_{Y}^{ - 1} \left[ {{\varvec{\upgamma}}_{Y,0} - {\mathbf{F}}\left( {{\mathbf{F}}^{\text{T}} {\varvec{\Gamma}}_{Y}^{ - 1} {\mathbf{F}}} \right)^{ - 1} \left( {{\mathbf{F}}^{\text{T}} {\varvec{\Gamma}}_{Y}^{ - 1} {\varvec{\upgamma}}_{Y,0} - {\mathbf{f}}_{0} } \right)} \right] $$

(14)

Substituting Eq. (14) into Eq. (8) will result in the required IRS ${\hat{\text{g}}}\left( {\mathbf{X}} \right)$ as [35]

$$ {\hat{\text{g}}}\left( {\mathbf{X}} \right) = \left[ {{\varvec{\upgamma}}_{Y,0} - {\mathbf{F}}\left( {{\mathbf{F}}^{T} {\varvec{\Gamma}}_{Y}^{ - 1} {\mathbf{F}}} \right)^{ - 1} \left( {{\mathbf{F}}^{\text{T}} {\varvec{\Gamma}}_{Y}^{ - 1} {\varvec{\upgamma}}_{Y,0} - {\mathbf{f}}_{0} } \right)} \right]^{\text{T}} {\varvec{\Gamma}}_{Y}^{ - 1} {\mathbf{Z}} $$

(15)

With the availability of the explicit expression for the required LSF using Eq. (15), the underlying reliability can be estimated using the FORM algorithm [4]. The steps in implementing FORM is not discussed here for the sake of brevity. The procedure will be denoted hereafter as Scheme KM. An SMRS generated using KM is expected to be accurate.

6 Improved Kriging Method

If the number of RVs is large, the use of CCD in generating SMRS using KM may not be feasible. The following strategies can be followed. In the final iteration, the cross terms and the necessary sampling points need to be considered only for the most significant RVs in sequence in order of their sensitivity indexes until the reliability index converges with a predetermined tolerance level. It is discussed in more detail by Azizsoltani and Haldar [13, 14]. The modified KM will be denoted hereafter as MKM. The accuracy in estimating the reliability using MKM is expected to be superior.

7 Verification Using a Case Study

Any new reliability evaluation procedure needs to be verified before it can be accepted. The author used a well-documented case study and 500,000 cycles of Monte Carlo simulation (MCS) for the verification purpose.

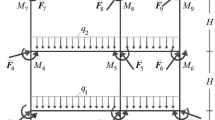
An actual 13-story steel moment frame building located in the Southern San Fernando Valley is considered as the case study. The building suffered significant damages during the Northridge earthquake of 1994. The building consisted of steel frames as shown in Fig. 1 [36]. Obviously, the frame is not expected to satisfy all the post-Northridge requirements.

Fig. 1

Significantly damaged steel building during the Northridge earthquake of 1994

The mean values of the material properties, E and F_y are considered to be 1.999E8 kN/m², and 3.261E5 kN/m², respectively. The mean values of the gravitational load for typical floors and roof are reported to be 40.454 kN/m and 30.647 kN/m, respectively, at the time of the earthquake.

The frame suffered different types of damages during the earthquake. Seven girders (G_d1–G_d7) and seven columns (C_d1–C_d7), identified in Fig. 1, suffered the most significant amount of damages (severely damaged). Near these elements, three girders (G_m1–G_m3) and three columns (C_m1–C_m3) are observed to be moderately damaged. Three completely undamaged columns (C_u1–C_u3) and three girders (G_u1–G_u3) without any sign of damage near the severely damaged columns are also considered to check the capabilities of the proposed procedure. Numerous earthquake time histories were recorded in the vicinity of the building. The 13-story steel frame is excited for 20 s by the time history of Northridge earthquake at Canoga Park station, as shown in Fig. 2, the closest station to the building exhibiting similar soil characteristics.

Fig. 2

Northridge time history measured at Canoga park station

For the serviceability limit states, 72 RVs are necessary to represent the frame. For the strength limit states of columns and girders, 157 and 101 RVs, respectively, are necessary. The sensitivity analysis was carried out and seven of them were found to be the most sensitive for both the serviceability and strength limit states. The reliabilities of the identified girders and columns in strength considering them as beam-column elements. To study the serviceability requirement, the permissible inter-story drift is considered not to exceed 0.7% of their respective height. The permissible value was increased by 125% according to the ASCE/SEI 7-10 [37].

The PFs of the columns and girders are estimated using MKM and the results are summarized in Table 1. The PFs of the girders are also summarized in Table 1. In addition, the PFs of the inter-story drift between the first floor and Plaza and between the seventh floor and sixth floor are estimated as summarized in Table 2. To establish their accuracy, 500,000 cycles of the classical MCS requiring about 1461 h of continuous running of a computer were carried out, and the results are also shown in the corresponding tables.

Table 1 Column and Girder Strength Reliability (Case of Study—13 story steel building)

Table 2 Interstory drift Reliability (Case of Study—13 story steel building)

The results shown in Tables 1 and 2 indicate that the PFs values are very similar to the numbers obtained by MCS indicating that they are accurate. The estimated PFs clearly correlate with the levels of damage (severe, moderate, and no damage). The results are very encouraging and document that estimated PFs can be correlated with different damage states. The results also establish the robustness of the algorithm in estimating PFs for high, moderate, and no damage states. The PFs of the highly and moderately damaged columns and girders are not in an acceptable range. The PFs for the inter-story drift between the first floor and Plaza and between the seventh floor and sixth floor clearly indicate that it will fail to satisfy the inter-story drift requirement. One can assume that the frame was designed by satisfying all the pre-Northridge design criteria that existed in the Southern San Fernando Valley area. This study clearly identifies weaknesses in them and justified the necessity of the post-Northridge design criteria. One can observe that the PFs of all girders are much higher than that of columns. It reflects the strong column and weak girder concept was used in designing these frames. However, very high PFs of the damaged girders are not acceptable and show the deficiency of the basic design. The PFs for serviceability LSFs are summarized in Table 2. They are very high and will not satisfy the reliability requirement.

The case study indicates that the proposed procedure significantly advanced the state of the art in the reliability evaluation of large structural systems excited by dynamic loadings including seismic loading applied in the time domain with few hundreds of deterministic FE-based analyses. The author believes that they developed novel reliability evaluation concepts by representing structures by FEs, explicitly considering major sources of nonlinearity and uncertainty, and applying dynamic loadings in the time domain. These features are expected to satisfy the deterministic community.

8 Conclusions

A novel concept is presented and verified by exploiting the advanced computational power and mathematical platforms in this paper. To generate the necessary implicit performance functions explicitly, a significantly improved SMRM concept is proposed. The Kriging method is used as the major building block. To establish the accuracy and validate the procedures, the estimated probabilities of failure for both strength and serviceability limit states are compared by using 500,000 Monte Carlo simulations. An actual 13-story steel moment frame building located in the Southern San Fernando Valley, California suffered a significant amount of damages during the Northridge earthquake of 1994. Few structural elements of the building suffered different levels of damage and some others did not. The proposed procedure identified the damage state of structural elements. The use of strong columns and weak beams concept is beneficial for dynamic (seismic) designs. The post-Northridge design criteria are found to very desirable. The study significantly advanced the state of the art in the reliability evaluation of large structural systems excited by dynamic loadings including seismic loading applied in the time domain with few hundreds of deterministic FE-based analyses. The proposed concepts of multiple deterministic dynamic response analyses of large complicated structures appeared to be reasonable and implementable, particularly considering existing enormous computational capabilities. The author believes that they propose alternatives to the random vibration approach and MCS have been met.