Learning Noise-Aware Correlation Filter for Visual Tracking

Abstract

Correlation filter has recently attracted much attention in visual tracking due to their excellent performance on both accuracy and efficiency. However, the adopted features, such as Colors, HOG and deep features, usually include noises and/or corruptions which might disturb the tracking performance. To handle this problem, we propose a novel noise-aware correlation filter method for robust visual tracking. In particular, we decompose the input feature matrix into a “clean” feature matrix and a sparse noise matrix, and then use the “clean” feature to train the correlation filter. To optimize the proposed correlation filter, we design an efficient ADMM (alternation direction of multipliers) solver. Extensive experimental results on the OTB-2013 dataset show that the proposed approach performs favorably against state-of-the-art trackers.

1 Introduction

Visual tracking is one of the most challenging and active tasks in computer vision and has drawn much attention due to its wide applications, such as video surveillance, human-computer interactions, and self-driving cars. Given the ground truth in the initial frame, the goal of visual tracking is to find all bounding boxes of the target object in subsequent frames. Despite many recent breakthroughs in visual tracking, it still remains challenge due to diverse factors, such as occlusion, object deformation, scale variation and background clutter.

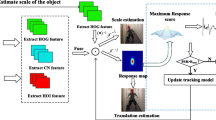
Correlation Filter (CF) has recently attracted much attention in visual tracking [1, 6, 7, 11, 14, 15, 24, 29,30,31] due to their excellent performance in both accuracy and efficiency. CF trackers employ the cyclic shifts to generate dense samples, and diagonalize them in the Fourier domain by using the Fast Fourier Transform (FFT). It enables trackers robust and high speed. The seminal work of CF tracking is proposed by Bolme et al. [1], which achieves hundreds of frames per second and high tracking accuracy. However, MOSSE only employs the simple feature to represent objects, i.e., brightness feature, without enough to be adopted in some complicated situations. To improve the tracking performance, most successful CF trackers use a discriminative object representation with either strong hand-crafted features such as HOG [7, 15, 24], color names [9, 24], or deep features [6, 8, 25]. Recent work has integrated deep features [25] trained on large dataset, such as ImageNet, to represent objects. In addition, multiple type of features are also employed together to robustly represent the tracked object, such as HOG features and color name [7, 24], and HOG features, color name and deep features [6, 8]. Although these trackers have achieved appealing results in both accuracy and computational efficiency, they ignore that these features might be polluted by noises or corruptions. As shown in Fig. 1, the bounding box of objects usually has several background information, which caused by occlusion or irregular shape of objects. Noises in features result in model drifting by influencing the learned appearance model and filter. Figure 2 shows the tracking results of Dual Correlation Filter (DCF) [15] on sequence Soccer. It illustrates that DCF will lose the object with noises in bounding box, which suggests that noises influence the tracking performance.

Fig. 1.

Some examples of noises in bounding boxes.

Motivated by the robust principal component analysis (RPCA) [3], Sui [28] decompose the feature matrix into a low-rank matrix and noise matrix. But the optimization of low-rank constraints refers to singular value decomposition (SVD). And SVD has high computation complexity and extremely time consuming. It influences the efficiency of trackers while real-time is a crucial factors in visual tracking. Therefore, we propose a simple and efficient feature decompose algorithms in this paper. According to [19,20,21,22, 28], we decompose the feature into the “clean” feature and noises. We do not impose the low-rank constraints on the “clean” feature and only impose the sparse constraint on the noises due to observations from Li et al. [17,18,19, 21, 22]. They think that the noise matrix is the sparse sample-specific corruptions, i.e., a few patches are corrupted and others are clean. Motivated by these works, we suppose that the noise in features is also sparse. We aim to learn the “clean” feature through imposing the sparse constraint on noises. The noise-aware filter is optimized by the learned “clean” feature for mitigate noises effects on filter. The simple feature decomposition is incorporated into CF tracking framework. It improves the tracking accuracy by suppressing noises effects on features and filters.

This paper makes the following contributions to CF tracking and related applications as follows. First, we propose a noise-aware correlation filter tracking algorithms based on feature decomposition. The noise-aware filter and “clean” feature can be jointly optimized in an unified framework. Second, we also design an efficient ADMM (Alternation Direction Method of Multipliers) algorithm [2] that can optimize the filter and the “clean” features in a framework. Third, extensive experiments are carried out on public benchmark datasets. The evaluation results demonstrate the effectiveness of the proposed approach against the baseline methods.

Fig. 2.

The example represents the effectiveness of our methods. Green, red, and blue box represents the ground truth, the tracking results of DCF, DCF$_{our}$, respectively. (Color figure online)

2 Related Work

Recently, CF has obtained great achievement in visual tracking due to its accuracy and computational efficiency. Bolme et al. [1] first introduce the CF into visual tracking, which achieves hundreds of frames per second, and high tracking accuracy. However, there is a problem about MOSSE that it only employs the simple brightness feature of image that isn’t enough to adapt to some complicated situations.

More and more discriminative features are utilized in tracking to represent objects for improving the performance, such as HOG [7, 15, 24], Color Names [9, 24] and deep features [6, 8, 25]. In addition, several trackers  [6,7,8, 24] employ multiple type features to represent the object for more robust tracking. To further enhance the ability to classify objects from the background, kernel tricks, which make the inseparable samples in low-dimension are mapped to the high-dimension space to achieve the purpose of classification, are used in CF tracking. Henriques et al. [14, 15] employ the kernel trick to improve performance. To adaptively employ complementary features, Tang et al. [30] propose a multi-kernel learning algorithm to improve performance. However, different kernels of MKCF may restrict each other in training and updating, which limits its improvement over KCF [15]. In addition, the increased computational cost of MKCF in comparison to KCF limits the tracking speed. Therefore, Tang et al. [31] employ a different way [30] to introduce the MKL into KCF. The way not only adaptively exploits multiple complementary features and non-linear kernels more effectively than MKCF, but also keeps relative high speed. CF framework usually faces a problem that boundary effect which is caused by utilizing a periodic assumption of the training samples to efficiently learn a classifier. To address the boundary effect, SRDCF [7] is proposed by introducing the spatially regularized into the learning of correlation filter to penalize the filter coefficients near the boundary. In CSR-DCF [24], spatial reliability map is constructed to adjust the filter support to the part of object suitable for tracking. To adapt the size variation, several adaptive scale processing tracker [5, 23] are investigated. Danelljan et al. [5] utilize the two correlation filters to capture the location translation and scale estimation, respectively. Li et al. [23] employ an effective scale adaptive scheme and integrate the HOG features and Color Name features to boost the tracking performance.

In addition, Danelljan et al. [8] utilize continuous convolution to integrate multi-resolution feature maps. The factorized convolution operator and the generative sample space model are introduced into tracking [6] for addressing the over-fitting and computational complexity. CFnet [32] is the first to introduce the correlation filter into a deep neural network as a differentiable layer. Sun et al. [29] treat the filter as the element-wise product of a base filter and a reliability term to learn the discriminative and reliable information for improving the tracker’s accuracy and robustness.

3 Review of Correlation Filters Tracking

In this section, we simply introduce the classical correlation filter tracking framework. Given the training set $T=[ (\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\ldots (\mathbf{x}_n,y_n)]$, we find a linear regression function $h(\mathbf{x})=\mathbf{w}^\mathbf{T }{} \mathbf{x}$ that minimizes the squared error over samples $\mathbf{x}_i$ and their regression targets $\mathbf{y}_i$. The model can be written as follows:

$$\begin{aligned} \begin{aligned}&\min _\mathbf{w} \sum _{i}(h(\mathbf{x}_i )- \mathbf{y}_i )^2+\lambda \Vert \mathbf{w}\Vert ^2 \end{aligned} \end{aligned}$$

(1)

where $\lambda$ is a regularization parameter that controls overfitting. Equation (1) has a closed-form, which is given by [26]

$$\begin{aligned} \begin{aligned}&\mathbf{w} = (\mathbf{X}^T\mathbf{X}+\lambda \mathbf{I})^{-1}{} \mathbf{X}^T\mathbf{y}. \end{aligned} \end{aligned}$$

(2)

where $\mathbf{X}$ is circulant matrix generated by the base sample $\mathbf x$, $\mathbf I$ is identity matrix. The per row of circulant matrix $\mathbf X$ is one virtual sample $\mathbf{x}_i$ obtained through the cyclic shift of the base sample $\mathbf{x}$. Let $\mathbf{y = [y}_1,\mathbf{y}_2,...,\mathbf{y}_n]^\mathbf{T}$ is a regression target of samples $\mathbf{X}$. Each element $\mathbf{y}_i$ is a regression target of $\mathbf{x}_i$.

To calculate in the Fourier domain, the solution (2) is transformed into the complex version as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{w} = (\mathbf{X}^H\mathbf{X}+\lambda \mathbf{I})^{-1}{} \mathbf{X}^H\mathbf{y}. \end{aligned} \end{aligned}$$

(3)

where $\mathbf{X}^H$ is the Hermitian transpose, that is the transpose of the complex-conjugate of $\mathbf X$, $\mathbf{X}^H = (\mathbf{X}^*)^T$. The circulant matrix $\mathbf X$ can be expressed as diagonal of $\mathbf x$ by the Discrete Fourier Transform (DFT) [12]:

$$\begin{aligned} \begin{aligned} \mathbf{X}={F}~diag{(\hat{\mathbf{x}})} F ^H \end{aligned} \end{aligned}$$

(4)

where $\hat{\mathbf{x}}$ denotes the DFT of $\mathbf{x}$, that is $\hat{\mathbf{x}}=\mathcal F(\mathbf{x})$, $diag(\mathbf{x})$ denotes the diagonal matrix of a vector $\mathbf x$. ${{\varvec{F}}}$ is a constant matrix that does not depend on the generating vector $\mathbf x$, as $\mathcal F(\mathbf z ) = \sqrt{n}F \mathbf z$. The notation n is the size of the generating vector $\mathbf x$. From now on, we will alway use a hat ${\hat{\mathbf{a}}}$ as shorthand for the DFT of vector $\mathbf a$.

The property (4) of circulant matrix can be applied to the solution (3), which is expressed as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{\hat{w}} = \frac{\hat{\mathbf{x}}^*\odot \mathbf{\hat{y}}}{\mathbf{\hat{x}}^*\odot \mathbf{\hat{x}}+\lambda } \end{aligned} \end{aligned}$$

(5)

where $\odot$ and the fraction denote element-wise product and division, respectively. And $\mathbf x^*$ represents the complex-conjugate of $\mathbf x$.

The Eq. (1) can be transformed into dual domain. The dual objective function can be written as follows:

$$\begin{aligned} \begin{aligned}&\min _\mathbf{\alpha } \frac{1}{4\lambda }\mathbf{\alpha }^T\mathbf{XX}^T\alpha + \frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} \end{aligned} \end{aligned}$$

(6)

where $\alpha$ is the dual variable. The two solutions from the objective function (1) and (6) are related by $\mathbf{w} = \frac{\mathbf{X}^T\alpha }{2\lambda }$. Here, for clarity and avoiding the calculation of cyclic matrix, the dual form is rewritten as:

$$\begin{aligned} \begin{aligned}&\min _\mathbf{\alpha } \frac{1}{4\lambda }\mathbf{\alpha }^T {{\varvec{C}}}(\mathbf{x }){{\varvec{C}}}(\mathbf{x })^T\alpha + \frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} \end{aligned} \end{aligned}$$

(7)

where ${{\varvec{C}}}(\mathbf{x })$ denotes the cyclic matrix generated by the base sample $\mathbf x$. The variable $\mathbf \alpha$ can be optimized efficiently in the Fourier domain:

$$\begin{aligned} \begin{aligned}&\mathbf{\hat{\alpha }} = \frac{\hat{\mathbf{y}}}{\frac{1}{2\lambda }{\hat{\mathbf{x}}}^*\odot {\hat{\mathbf{x}}} + \frac{1}{2}} \end{aligned} \end{aligned}$$

(8)

where the fraction denote element-wise division.

The final response map $\mathbf \phi$ is calculated through the following equation:

$$\begin{aligned} \begin{aligned}&\mathbf \phi =\mathcal F^{-1}(\hat{\mathbf{w}}\odot \hat{\mathbf{x}}) ~= \mathcal F^{-1}(\hat{\mathbf{k}}^{\hat{\mathbf{x}}\hat{\mathbf{z}}} \odot \hat{\alpha }) \end{aligned} \end{aligned}$$

(9)

where $\mathcal F^{-1}$ denotes the inverse operation of DFT, ${{\hat{\mathbf{k }}}^{\hat{\mathbf{x }}{\hat{\mathbf{z }}}}}$ is the kernel of training samples $\mathbf x$ and candidate patches $\mathbf z$. Then we can localize the target in current frame through the response map.

CF trackers usually employ several hand-craft features (e.g. HOG features, Color Name features) or deep learning features to represent the object for robust tracking. However, these features might be polluted by noises or corruptions. According to Eqs. (8) and (9), noises in features will influence the learned appearance model and filter and thus limit the tracking performance. As shown in Fig. 2, DCF and DCF$_{our}$ can both work well when the tracked object has not noises. However, DCF loses the tracked object but the DCF$_{our}$ can successfully track the object when the object includes the noises. It illustrates that noises influence the learned filters and then limit the trackers performance. Therefore, we propose a noise-aware correlation filter tracking algorithm to mitigate the noises effect on filters. In next section, we will mainly introduce how the algorithms works in correlation filter tracking framework.

4 Methods

In this section, we give a detailed description about how to learn jointly noise-aware filter and “clean” feature through feature decomposition for suppressing the influence of noises.

4.1 Noise-Aware Correlation Filter

Objects can be represented using hand-craft features (e.g. HOG features [10], Color Name features [33]). Besides the hand-craft features, the deep features extracted from the VGG model [27] also are applied to represent the object. However, whether hand-craft features or deep features, they may be polluted by noises or corruptions. RPCA [3] has a powerful capability to suppress noises or corruptions. But the optimization of RPCA refers to singular value decomposition (SVD). And SVD has high computation complexity and extremely time consuming. It influences the efficiency of trackers. Therefore, we propose a simple and efficient feature decompose algorithms, which decomposes the feature $\mathbf x$ into the “clean” feature $\mathbf z$ and noises $\mathbf{e}$. And we impose the sparse constraint on noises and do not impose the low-rank constraint on the “clean” feature. The learned “clean” feature is used to optimize the noise-aware filter for mitigate noises effects.

$$\begin{aligned} \begin{aligned}&\mathbf{x} = \mathbf{z} + \mathbf{e} \end{aligned} \end{aligned}$$

(10)

The Eq. (10) is incorporated into CF tracking framework to jointly optimize variables. The “clean” feature $\mathbf z$ is used to optimize the noise-aware filter and make the filter more robust. The dual form model (7) can be reformulated as Eq. (11), which can learn the “clean” features and the noise-aware filter to improve the accuracy and robustness.

$$\begin{aligned} \begin{aligned}&\min _\mathbf{\alpha ,z,e} \frac{1}{4\lambda }\mathbf{\alpha }^T C(\mathbf{z}) C(\mathbf{z})^T\alpha + \frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} + \beta \mathbf{\Vert e\Vert }_0 \\&s.t.~\mathbf{x} =\mathbf{z} +\mathbf{e} \end{aligned} \end{aligned}$$

(11)

where $\lambda$ is a regularization parameters that controls overfitting, and $\beta$ is balanced parameter.

Because the $l _0$ norm is non-convexity, it is difficult to directly optimize the Eq. (11). To overcome the obstacles, we will use convex relaxation to relax the non-convex sparsity terms into the convex sparsity terms. We replace the $l _0$ norm with $l _1$ norm using the convex relaxation. Thus, the Eq. (11) can be relaxed as:

$$\begin{aligned} \begin{aligned}&\min _\mathbf{\alpha ,z,e} \frac{1}{4\lambda }\mathbf{\alpha }^T{{{\varvec{C}}}(\mathbf{z}){{\varvec{C}}}(\mathbf{z})}^T\alpha + \frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} + \beta \mathbf{\Vert e\Vert }_1 \\&s.t.~\mathbf{x} = \mathbf{z} +\mathbf{e} \end{aligned} \end{aligned}$$

(12)

Although the Eq. (12) seems complex and is not joint convex, subproblem of each variable is convex by fixing other variables and has a closed-form solution. Therefore, the model can be optimized by the ADMM (alternating direction method of multipliers) algorithm [2]. As demonstrated in the experiments, the parameters of Eq. (12) are easy to adjust, and the tracking performance is insensitive to parameter variations.

4.2 Optimization

In this section, we mainly introduce how to solve the objective function (12). Although the variables of the (12) are not joint convex, the subproblem of each variable with others fixed is convex and has a closed-form solution. The ADMM is a effective solver of the problems like (12). By introducing augmented Lagrange multipliers, the optimization function (12) can be written as the following augmented Lagrange function:

$$\begin{aligned} \begin{aligned}&\mathcal {L}_{(\mathbf \alpha ,\mathbf{z,e})} = \frac{1}{4\lambda }\mathbf{\alpha }^T{{{\varvec{C}}}(\mathbf{z}){{\varvec{C}}}(\mathbf{z})}^T\alpha +\frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} +\beta \mathbf{\Vert e\Vert }_1 \\&~~~~~~~~~~~~~~~~ + \frac{\mu }{2}\Vert \mathbf{x - z - e + \frac{p}{\mu }}\Vert ^2_2 - \frac{1}{2\mu }\mathbf{\Vert p\Vert }^2_2 \end{aligned} \end{aligned}$$

(13)

where $\mu > 0$ is the penalty parameter and $\mathbf p$ is the Lagrangian multipliers. The ADMM method updates one of the variables by minimizing $\mathcal {L}$ with other variables fixed. By updating these variables iteratively, the convergence can be guaranteed [2]. Besides the Lagrangian multipliers $\mathbf p$, there are three variables that need to be updated, including $\mathbf \alpha ,\mathbf{z,e}$. The closed form solution of each subproblems are as follows.

Update $\alpha$ (with others fixed): The optimization (13) with respect to the variable $\mathbf \alpha$ can be formulated as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{\alpha } = \mathop {\text {argmin}}_\mathbf{\alpha } \frac{1}{4\lambda }\mathbf{\alpha }^T{{{\varvec{C}}}(\mathbf{z}){{\varvec{C}}}(\mathbf{z})}^T\alpha + \frac{1}{4}\mathbf{\alpha }^T\mathbf{\alpha } - \mathbf{\alpha }^T\mathbf{y} \end{aligned} \end{aligned}$$

(14)

For calculating the variable $\mathbf \alpha$, we take the derivative of the $\mathbf \alpha$-subproblem (14) and set it to 0. The variable $\mathbf \alpha$ has the closed-form solution. With some algebra, the closed-form solution of the variable $\mathbf \alpha$ can be formulated as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{\alpha } = (\frac{1}{2\lambda }{{{\varvec{C}}}(\mathbf{z}){{\varvec{C}}}(\mathbf{z})}^T + \frac{1}{2}{} \mathbf{I})^{-1}\mathbf y \end{aligned} \end{aligned}$$

(15)

where $\mathbf I$ is the identity matrix. The amount of computation cost of Eq. (15) is large, mainly from matrix inverse and multiplication in spatial domain. For the fast operation in Fourier domain, the property (4) of cyclic matrix is introduced into the solution (15). The variable $\mathbf \alpha$ is updated with only the base sample as follows:

$$\begin{aligned} \begin{aligned}&{\mathbf{\hat{\alpha }}^{k+1}} = \frac{\hat{\mathbf{y}}}{\frac{1}{2\lambda }({\hat{\mathbf{z}}}^*)^k\odot {{\hat{\mathbf{z}}}^k} + \frac{1}{2}} \end{aligned} \end{aligned}$$

(16)

where the fraction denotes the element-wise division. Finally, the $\mathbf \alpha$ can be obtained via $\alpha = \mathcal F^{-1}(\mathbf{\hat{\alpha }})$.

Update z (with others fixed): The $\mathbf z$ is updated through solving the subproblem (17) corresponding to $\mathbf z$ with the closed-form solution.

$$\begin{aligned} \begin{aligned}&\mathbf{z} = \mathop {\text {argmin}}_\mathbf{z} \frac{1}{4\lambda }\mathbf{\alpha }^T{{{\varvec{C}}}(\mathbf{z}){{\varvec{C}}}(\mathbf{z})}^T\alpha + \frac{\mu }{2}\Vert \mathbf{x - z - e + \frac{p}{\mu }}\Vert ^2_2 \end{aligned} \end{aligned}$$

(17)

To solve and calculate efficiently in Fourier domain, the Eq. (17) is formulated as follows by Parsevaal’s theorem:

$$\begin{aligned} \begin{aligned} \begin{aligned}&\mathbf{\hat{z}} = \mathop {\text {argmin}}_\mathbf{\hat{z}} \frac{1}{4\lambda }\mathbf{\hat{\alpha }}^Hdiag(\mathbf{\hat{z}})diag(\mathbf{\hat{z}}^*)\hat{\alpha }+ \frac{\mu }{2}\Vert \mathbf{\hat{x} - \hat{z}-\hat{e} +\frac{\hat{p}}{\mu }}\Vert ^2_2 \\ \end{aligned} \end{aligned} \end{aligned}$$

(18)

where $diag(\mathbf{z})$ denotes the diagonal matrix of a vector $\mathbf z$. With some algebra, the first term of Eq. (18) can be transformed as the following forms:

$$\begin{aligned} \begin{aligned} \begin{aligned}&\mathbf{\hat{z}}= \mathop {\text {argmin}}_\mathbf{\hat{z}} \frac{1}{4\lambda }\mathbf{(\hat{\alpha }\odot \hat{z})}^H\mathbf{(\hat{\alpha }\odot \hat{z})} + \frac{\mu }{2}\Vert \mathbf{\hat{x} - \hat{z}-\hat{e} +\frac{\hat{p}}{\mu }}\Vert ^2_F \end{aligned} \end{aligned} \end{aligned}$$

(19)

where the derivative of $\mathbf{(\hat{\alpha }\odot \hat{z})}^H\mathbf{(\hat{\alpha }\odot \hat{z})}$ is $2(\mathbf{\hat{\alpha }}^*\odot \mathbf{\hat{\alpha }}\odot {\hat{\mathbf{z}}})$ with some algebra. The solution of $\hat{\mathbf{z}}$ is obtained by setting the derivative of (19) to 0.

$$\begin{aligned} \begin{aligned}&\mathbf{\hat{z}}^{k+1} = \frac{\mathbf{\mu (\hat{x}-\hat{e}^k)+\hat{p}^k}}{\frac{1}{2\lambda }\mathbf{(\hat{\alpha }^*)}^{k+1}\odot \mathbf{\hat{\alpha }}^{k+1}+\mu ^k} \end{aligned} \end{aligned}$$

(20)

where fraction denotes the element-wise division. Finally, the “clean” feature $\mathbf z$ can be obtained using the formula: $\mathbf{z} = \mathcal F^{-1}(\hat{\mathbf{z}})$.

Update $\mathbf e$ (with others fixed): The optimization (13) with respect to the variable $\mathbf e$ is formulated as follows:

$$\begin{aligned} \begin{aligned} \begin{aligned}&\mathbf{e} =\mathop {\text {argmin}}_\mathbf{e}\, {\beta \mathbf \Vert e\Vert }_1 +\frac{\mu }{2}\Vert \mathbf{x-z-e + \frac{p}{\mu }}\Vert ^2_2\\ \end{aligned} \end{aligned} \end{aligned}$$

(21)

The noise $\mathbf e$ is obtained by the soft-thresholding (or shrinkage) method [4] with closed-form solution:

$$\begin{aligned} \begin{aligned}&\mathbf{e}^{k+1} = \mathcal S_{\frac{\beta }{\mu ^k}}(\mathbf{x}-\mathbf{z}^{k+1}+\frac{\mathbf{p}^k}{\mu ^k}) \end{aligned} \end{aligned}$$

(22)

where $\mathcal S_{\frac{\beta }{\mu }}(\mathbf x)$ is the soft-thresholding operator for a vector $\mathbf x$ with parameter $\frac{\beta }{\mu }$. Here, the $\mathcal S_{\frac{\beta }{\mu }}(\mathbf{x})$ can be calculated through the Eq. (23).

$$\begin{aligned} \begin{aligned} \begin{aligned}&\mathcal S_{\frac{\beta }{\mu }}(\mathbf{x}) = (sign(\mathbf{x}))\odot (\max (0,|\mathbf{x}| - \frac{\beta }{\mu })) \end{aligned} \end{aligned} \end{aligned}$$

(23)

Besides the above variables, the Lagrange multiplier $\mathbf y$ is updated by following the Eq. (24):

$$\begin{aligned} \begin{aligned}&\mathbf{p}^{k+1} = \mathbf{p}^k + \mu ^k(\mathbf{x}-\mathbf{z}^{k+1}-\mathbf{e}^{k+1}) \end{aligned} \end{aligned}$$

(24)

Since each subproblem of (13) is convex, we can guarantee that the limit point by our algorithm satisfies the Nash equilibrium conditions [35]. The details of optimization procedure are shown in Algorithm 1.

4.3 Tracking

In this section, we briefly introduce the process of the localization and update steps of the proposed algorithm.

Localization. Features are extracted from the searching area in current frame. We employ the learned variables $\mathbf z,\alpha$ in previous frame to locate the object in current frame. The response map can be obtained as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{\phi } = \mathcal F^{-1}({\hat{\mathbf{k}}^{\hat{\mathbf{x}}\hat{\bar{\mathbf{z}}}}} \odot \hat{\alpha }) \end{aligned} \end{aligned}$$

(25)

where ${\hat{\mathbf{k}}}^{{\hat{\mathbf{x}}}{\hat{\bar{\mathbf{z}}}}}$ denotes the kernel between ${\hat{\bar{\mathbf{z}}}}$ and $\hat{\mathbf{z}}$, and the ${\hat{\bar{\mathbf{z}}}}$ represents the learned target appearance model using the “clean” feature, the $\hat{\mathbf{x}}$ denotes the feature in current frame. We locate the tracked object using the response map.

Learning-Update. The searching area is extracted in current frame. The extracted feature from searching area are feed into the Eq. (13) to optimize the dual variable and the “clean” feature. For capturing the variation of tracked target’s appearance, the dual variable and the target appearance model are updated by an autoregressive model with learning rate. The updated strategy of dual variable $\mathbf \alpha$ and appearance model ${\hat{\bar{\mathbf{z}}}}$ follows the following formulation.

$$\begin{aligned} \begin{aligned}&\mathbf{\hat{\alpha }}^t = (1- \eta )\mathbf{\hat{\alpha }}^{t-1} + \eta \mathbf{\hat{\alpha }} \\&\mathbf{\hat{\bar{z}}}^t = (1- \eta )\mathbf{\hat{\bar{z}}}^{t-1} + \eta \mathbf{\hat{z}} \end{aligned} \end{aligned}$$

(26)

where $\eta$ is learning rate. According to the above solution procedure, it does not refers to the large amount of computation operations like matrix inverse.

5 Experiments

In this section, we mainly introduce the implementation details of our model, evaluation datasets and evaluation metrics, and the analysis of experimental results compared with baseline and other state-of-the-art trackers in public benchmark.

5.1 Experimental Setup

Implementation Details and Parameters: To demonstrate the effectiveness of our model, we select the two different baseline trackers to implement the model. They are dual correlation filter methods (DCF) [15] based on hand-craft features and HCF [25] based on the deep features. The two baseline models both employ the dual model to optimize the problem. Firstly, the implementation details of embedding our model in DCF (DCF$_{our}$) are introduced. Standard HOG [10] descriptors are used to represent the object in DCF. We only embedded the feature decomposition model in DCF to jointly learn noise-aware filters and the “clean” feature for improving tracking performance. The $\beta$ and $\lambda$ in Eq. (13) is set to 0.005 and 0.1, respectively.

Next, we mainly introduce the implementation details of embedding our model in HCF. Ma et al. [25] extract three layers deep features from VGGNet [27], that are conv4,conv3-4 and conv5-4. The three convolution features independently learn the filter and the appearance model. The final response map is fused by three different response maps obtained by the three convolution features. We only implement noise-aware correlation filter model based on different convolution layers. The $\beta$ and $\lambda$ in Eq. (13) is set to 0.01 and 1e-4, respectively. The experiments are carried out on a PC with an Intel i7 4.2 GHz CPU and 32G RAM.

As seen from the above section, the parameter settings for DCF$_{our}$ and HCF$_{our}$ have great discrepancy, but this discrepancy is considered reasonable because DCF$_{our}$ and HCF$_{our}$ are different models. All parameters are optimal by varying them on a certain scope. Moreover, when we slightly adjust the parameters, tracking performance only change a little and Table 1 shows the results of the proposed method DCF$_{our}$ and HCF$_{our}$ with different parameters.

Table 1. The precision rate (PR) of the proposed method DCF$_{our}$ and HCF$_{our}$ with different parameters.

Datasets and Evaluation Metrics: Our method is evaluated on benchmark dataset: OTB-2013 [34] with 50 sequences. The images are annotated with ground truth bounding boxes and various visual attributes. For the OTB-2013 dataset, we employ the one-pass evaluation (OPE) and use two metrics: precision rate (PR) and success rate (SR). PR is the percentage of frames whose output location is within the given threshold distance of ground truth. That is to say, it computes the average Euclidean distance between the center locations of the tracked target and the manually labeled ground-truth positions of all the frames. SR is the ratio of the number of successful frames whose overlap between predicted and ground truth bounding box is larger than a threshold. In the legend, we report the area under curve (AUC) of success plot and precision score at 20 pixels threshold corresponding to the one-pass evaluation for each tracking method.

Compared Trackers: To identify the effectiveness of our model, we evaluate the proposed model with comparisons to several state-of-the-art methods for evaluations. Several trackers based on correlation filter are selected to evaluate the performance, including DSST [5], KCF [15], CSR-DCF [24], SRDCF [7] and SAMF [23]. In addition, we also select several representative trackers to compare with our methods, Struck [13], TLD [16], SCM [36].

Table 2. The Mean FPS compared with DCF, KCF, DSST, SAMF, CSR-DCF trackers.

5.2 Tracking Speed

The tracking speed is crucial in many realistic tracking applications. We therefore generalize the tracking speed about DCF and DCF$_{our}$ in Table 2. In addition, Table 2 enumerates other trackers based on correlation filter, including DCF, KCF, DSST, SAMF, SRDCF, CSR-DCF. It is verified that DCF$_{our}$ performs at about 77.52 FPS (frames per second) to achieve real-time tracking (equivalent to approximately 20 FPS) although it achieves the lower tracking speed than DCF.

RPCA [3] has a powerful capability to suppress noises or corruptions. RPCA is a NP-hard problem because it simultaneously involves $rank$ and $\ell _0$. To overcome these obstacles, a convex relaxation of the problem is proposed, we use $\Vert \cdot \Vert _*$ and $\ell _1$ to replace $rank$ and $\ell _0$, respectively. It also should be note that although the convex relaxations are leveraged, the obtained problem is still non-convex. Fortunately, this problem is convex with respect to each of them when others are fixed. ADMM algorithm [2] has proven to be an efficient and effective solver of RPCA. However, it involves SVD in the process of iterative solution using ADMM. SVD has high computational complexity and extremely time consuming. Although the proposed method is also optimized by ADMM, SVD is not involved in the optimization.

Table 3. The precision rate (PR%) and success rate (SR%) on OTB-2013 over DCF, DCF$_{our}$, HCF, and HCF$_{our}$, DSST, SAMF, SRDCF, CSR-DCF, Struck, TLD, and SCM

5.3 Comparison with Baseline Methods

We compare our methods with the baseline trackers to demonstrate the strength of our proposed methods in this part.

Overall Evaluation: To illustrate the effectiveness of our proposed model, we implement the model in DCF and HCF, named DCF$_{our}$ and HCF$_{our}$, respectively. Table 3 shows the overall evaluation results between DCF, HCF and DCF$_{our}$, HCF$_{our}$ in OTB-2013. Benefiting from our proposed model, the DCF$_{our}$ outperforms DCF in PR/SR by 1.1%/0.6% and 0.4%/1.9%, respectively. HCF$_{our}$ achieves slight improvement over HCF in PR. But HCF$_{our}$ exceeds 1.9% in SR over HCF. This evaluative performance illustrates that the feature decomposition scheme can improve the CF tracking performance. Table 4 represents tracking performance on several challenging factors between our trackers and the baseline trackers.

Table 4. Attributed-based PR/SR on OTB-2013 compared with DCF, HCF, SRDCF, CSR-DCF, SAMF, KCF, DSST trackers.

Attribute-Based Evaluation: We further analyze the tracking performance under different challenging attributes (e.g., background clutter (BC), occlusion (OCC), fast motion (FM)) annotated in the benchmark OTB-2013. Table 4 shows PR and SR of one-pass evaluation (OPE) for ten main challenging factors. We mainly take DCF$_{our}$ and DCF as an example to analysis the evaluative results. According to Table 4, we have the following observations.

First, our model is effective in handling motion blur (MB). In general, MB results in appearance degradation. And how to learn a good feature is critical to address the MB challenge. The DCF$_{our}$ achieves superior performance in PR/SR by 6.2%/2.2% over DCF. In comparison with the baseline, the excellent performance in MB illustrates DCF$_{our}$ can learn the “clean” feature to better represent objects. Second, our method also achieve excellent performance in handling BC and OCC. BC and OCC lead to features to be disturbed by the background. As shown in Table 4, DCF$_{our}$ outperforms DCF in PR/SR in 3.9%/1.6% and 1.8%/1.0% over BC and OCC, respectively. It demonstrates that the learned “clean” feature and noise-aware filter help to suppress the interference of noises. Finally, our method also represents the powerful strength on scale variation (SV) and illumination variation (IV). The critical important point is how to capture the variation of objects caused by the two challenging factors. For SV and IV, DCF$_{our}$ trackers both achieve the superior performance in PR/SR over baseline. Compared the baseline, the DCF$_{our}$ promotes 2.1%/0.8% and 2.6%/1.0% in SV and IV. It demonstrates our model can capture the variation of objects to learn the appearance model and the robust filter.

In addition, our method also achieves excellent performance in other challenging factors (fast motion (FM), low Resolution (LR)) and several factors (in-plane rotation (LPR), out-of-plane rotation (OPR)). In summary, the learned feature can better represent the object and optimize the filter.

5.4 Comparison with State-of-the-Art Trackers

Overall Evaluation: For comprehensive evaluation, we select several state-of-the-start trackers, including DSST [5], KCF [15], CSR-DCF [24], SRDCF [7], SAMF [23], Struck [13], TLD [16] and SCM [36] to compare with our proposed methods. The Table 3 represents the evaluation results between our proposed model and comparison trackers. As shown in Table 3, DCF$_{our}$ outperforms DSST in PR/SR while DCF achieves lower performance than the DSST in PR/SR. DCF$_{our}$ achieves comparable performance in PR/SR against KCF. This observation strongly illustrates that the proposed feature decomposition can help to improve the performance of CF trackers.

Attribute-Based Evaluation: We also select several trackers, including DSST [5], KCF [15], CSR-DCF [24], SRDCF [7] and SAMF [23] to evaluate the performance on different challenging attributes. Table 4 shows PR and SR of one-pass evaluation (OPE) for ten main challenging factors in OTB-2013 benchmark, including fast motion (FM), background clutter (BC), motion blur (MB), deformation (DEF), illumination variation (IV), low resolution (LR), occlusion (OCC) and scale variation (SV), respectively.

In this experimental analysis, we mainly focus on DCF and DCF$_{our}$ to analyze the performance of this proposed algorithm. According to Table 4, we have the following observations. The first conclusion is that the proposed feature decomposition can benefit the CF trackers to learn a “clean” feature to deal with the MB. In OTB-2013, DCF is lower than DSST in PR but the DCF$_{our}$ is greater than DSST and even outperforms KCF in PR. Although the performance of DCF$_{our}$ is still lower than SAMF, CSR-DCF, SRDCF, HCF, it is explained that DCF$_{our}$ is only based on the DCF to incorporate feature decomposition without any improvement while these extension trackers employ several tricks such as rich features and updating strategy besides their own improvement. The second conclusion is that our method also help to improvement the tracker’s performance in BC and OCC. According to Table 4, DCF$_{our}$ even outperforms the SAMF, KCF and DSST in PR for BC. Finally, it is observed that our method also improves the strength in handling SV and IV. In OTB-2013 benchmark, the performance of DCF$_{our}$ outperforms the DSST in PR/SR while the performance of DCF$_{our}$ is still lower than these trackers that have scale processing, including DSST, SAMF, SRDCF, CSR-DCF, HCF. Because the DCF$_{our}$ have no the scale process model and only mixes the feature decomposition scheme to learn “clean” feature and noise-aware filter. In summary, the proposed feature decomposition learns more robust filter and “clean” feature to improve the performance.

6 Conclusion

In this paper, feature decomposition is introduced into correlation filter tracking to learn “clean” feature and noise-aware filter for improve the tracking accuracy and robustness. The “clean” feature and noise-aware filter are jointly optimized in an unified framework to mitigate noises effect in filters and features. The proposed tracking framework utilizes the learned “clean” feature to represent objects and the noise-aware filter to classify the object from background. As a result, it has the advantages of several existing correlation filter trackers such as suppressing the influence of noises. Both qualitative and quantitative evaluations on challenging datasets demonstrate that the effectiveness of proposed tracking algorithm against baseline methods.