Randomized Response Techniques

Abstract

There are situations when we need information on sensitive features/characteristics of the individuals in a population. Usual sampling techniques based on ‘direct’ questionnaire may not be fruitful and are likely to lead to ‘refusal’ or ‘untruthful’ reporting. To overcome such undesirable consequences, randomized response techniques [RRTs, in short] have been introduced and extensively used in real-life situations. We discuss some salient features of this technique.

2.1 Introduction

Almost half a century back, randomized response technique/methodology [RRT/RRM] was first introduced and popularized by Warner. The idea is to be able to elicit a truthful response on sensitive issues(s) from the sampled respondents, so that eventually reliable estimates of some of their feature(s) can be estimated for the population as a whole. Since then, survey theoreticians and survey practitioners have contributed significantly in this area of survey methodological research.

Warner (1965) introduced an ingenious device to gather reliable data relating to such issues that may attach unethical stigmas in a civilized society. Therefore, direct questionnaire method is likely to result in refusal/denial or occasionally masked untruthful response. In the context of a society, issues such as abortions, spouse-mishandling, finding HIV tests positive, underreporting income tax returns, false claims for social benefits may have sensitive/unethical stigmas attached. People generally tend to hide public revelations of such vices.

In such circumstances, Warner suggested a way to avoid attempting to collect direct responses (DRs) from the selected respondents—either individually or in groups. Instead, he recommended implementation of what is termed as randomized response technique (RRT) in order to collect information from each sampled respondent when a stigmatizing issue is under contemplation in a study.

There is a huge amount of the published literature in this area of applied research. We refer to an excellent expository early book on RRT by Chaudhuri and Mukerjee (1988). Hedayat and Sinha (1991), Chap. 11, also provides a fairly complete account of RRTs. Two most recent books (Chaudhuri 2011; Chaudhuri and Christofides 2013) are worth mentioning as well.

2.2 Warner’s Randomized Response Technique [RRT]

To fix ideas, we consider sampling of individuals from a reference survey population in order to estimate the population proportion of a specific feature such as false claims for social benefits which is likely to be stigmatizing in nature. Therefore, direct questionnaire procedure is likely to be ruled out. In this context, Warner (1965) suggested the following approach.

Note that we are addressing the issue of eliciting truthful information on a sensitive qualitative feature [SQlF], with exactly one of the binary responses [yes/no] attached to each individual in the population, and we are interested in estimation of the population proportion P of ‘yes’ response(s) based on our study of the sampled respondents. The problem is to provide (i) a method of ascertaining truthful responses from the respondents facing the SQlF in the surveyed population and (ii) (unbiased) estimator of P. Generally, simple random sampling with replacement of respondents from the reference population [presumably large] is contemplated.

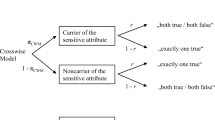
With reference to a single SQlF, its possession [yes] will be denoted by the attribute Q and its non-possession [no] will be denoted by the negation of Q, that is, $\bar{Q}$. The simplest related question technique of Warner (1965) refers to preparation of two identical and indistinguishable decks of cards with known multiple but unequal number of copies of both. One set [Set I] will have the instruction on the back of each card: Answer Q truthfully. Naturally, the truthful response should be ‘yes’ in case the respondent possesses the attribute Q and ‘no’ otherwise. The other set [Set II] deals with the instruction: Answer $\bar{Q}$ truthfully. This time a response of ‘yes’ would mean the respondent does not possess Q; otherwise, the response is ‘no’ implying that the respondent does possess Q. We may denote by p the known proportion of cards of Q category so that $1-p$ is the proportion of cards of $\bar{Q}$ category. A general instruction is given to all respondents: Each respondent is to select one card at random and with replacement out of the full deck and act as per the instruction given at the back of the selected card. The respondents are supposed to report only the yes/no answers—without divulging what kind of card had been selected by them. Naturally, this randomization device of selection of a card ensures that a respondent can make a choice of Q with probability p or a choice of $\bar{Q}$ with probability $1-p, 0< p \ne 0.5 < 1$, being known beforehand. It is believed that this randomization mechanism will convince the respondent about retaining the confidentiality of the response [yes/no] provided by him/her, without disclosing the choice of the card bearing the label Q or $\bar{Q}$ to the interviewer! In other words, the investigator is not to be told about the specific question chosen/answered by the respondent. For obvious reason, this method is also known as mirrored question design. See Blair et al. (2015) for descriptions of this and a few more RRMs. Routine formulae are there to work out the details of estimation, etc., in this and various other complicated randomization frameworks. In this simple randomized response framework, we proceed as follows toward unbiased estimation of P:

Note that a ‘yes’ answer has two sources: choice of one card from Set I, followed by ‘yes’ response, or choice of one card from Set II, followed by ‘yes’ response. Therefore, $P[yes] = pP + (1 - p)(1 - P) = P(2p - 1) + (1 - p)$. This we equate to the sample proportion of ‘yes’ responses among the total number of responses.

If there are n respondents and out of them, eventually, some f of them report ‘yes,’ then we have the defining equation:

$$ f/n = P(2p - 1) + (1 - p) $$

whence

$$ {\hat{P}} = \frac{f/n - (1 - p)}{2p - 1}. $$

It is seen from the above why we need the condition: $p \ne 0.5$. It follows that

$$ (i) V ({\hat{P}}) = P(1 - P)/n + p(1 - p)/ n(2p - 1)^{2} $$

$$\begin{aligned} (ii) \hat{V}&= p(1 - p) / n(2p - 1)^{2} \nonumber \\&{\quad } + [(1 - p)^{2} + {\hat{P}}(2p - 1) - f(f - 1) / n(n - 1)]/n(2p - 1)^{2}. \end{aligned}$$

This last expression, when square-rooted, gives what is known as the estimated standard error (s.e.) of ${\hat{P}}$.

Remark 2.1

The above results are based on the fact that f follows binomial distribution with parameters $(n, \theta )$ where n is the sample size [number of respondents] and $\theta = P(2p - 1) + (1 - p)$, being the probability of ‘yes’ response by a respondent under the RRM in use. It is known that f / n serves as an unbiased estimate for $\theta$ and $f(f - 1)/n(n - 1)$ serves as an unbiased estimate for $\theta ^{2}$. The rest are simple algebraic manipulations. We will refer to this method as RRM1.

Illustrative Example 2.1

We choose $n = 120$ and $p = 0.40$. Suppose the survey yields $f = 57$. This suggests

$$\begin{aligned} {\hat{P}}&= [57/120-0.60]/[-0.20] = 0.625; s.e. \nonumber \\ (\hat{P})&= \sqrt{24/48 + [.36 - .125 - .2235]/48} = 0.0724. \end{aligned}$$

Remark 2.2

Use of both versions [affirmative and negative] of the sensitive question Q may, at times, lead to confusion among the respondents. This was soon realized, and the RRT was accordingly modified by introducing what is called unrelated questionnaire method. We will designate this method as RRM2. This is described below.

Once again, we are in the framework of eliciting truthful response on the sensitive question Q but using a modified version of the RRT described above. This time, again, we form two sets of cards, and for the Set I, we keep the same instruction on the back of each card. For Set II, we rephrase the instruction by introducing a simple-minded question like: Were you born in the first quarter of a year? This question is denoted by the symbol $Q^{*}$ so that it also has two forms of the true reply: ‘yes’ for the affirmative reply and ‘no’ for its negation. When this RRT of eliciting response is executed, the chance of a ‘yes’ response is given by: $pP + (1 - p)/4$. This is because in a random sample of respondents about 1 / 4th are likely to have been born in the first quarter of a year. As in the above, this is equated to the sample proportion of ‘yes’ responses, i.e., f / n, and thereby, we obtain $\hat{P} = [f/n - (1 - p)/4]/p$. It is a routine task to work out $V(\hat{P})$, and this is given below:

$$\begin{aligned} V({\hat{P}})&= (1-p + 4pP)(3 +p -4pP)/16np^{2} \nonumber \\&= [(1-p)(3 +p) + 8p(1 +p)P -16p 2P^{2}]/16np^{2}. \end{aligned}$$

To compute $\hat{V}(\hat{P})$, in the above expression, we have to replace P by $\hat{P}$ which is already shown above. Further, also we need to replace $P^{2}$ in the above by an expression to be derived from the defining equation:

$$ f(f - 1)/n(n - 1) = [pP + (1 - p)/4]^{2} $$

upon expansion of the RHS expression and replacement of P by $\hat{P}$ derived earlier. Once estimated variance estimate is obtained, we compute s.e. of the estimate by taking the square root of the above quantity. Note that this time the distribution of f is binomial with parameters $(n, \eta = p P + (1 - p)/4)$.

Illustrative Example 2.2

We choose $n = 120$ and $p = 0.40$. Suppose survey yields $f = 57$. This suggests

$\hat{P} = [57/120 - 0.15]/[0.40] = 0.8125.$

Estimating equation for $\hat{P^{2}}$ is given by

$$\begin{aligned} 0.2235&= p^{2}P^{2} + p(1-p)P/2+(1-p)^{2}/16 = 0.16P^{2} + 0.0975+0.0225; \nonumber \\ 0.1035&= 0.16P^{2} ; \hat{P^{2}} = 0.6469. \end{aligned}$$

$$ {\hat{V}}({\hat{P}}) = [2.04 + 1.56 - 1.6560]/307.2 = 0.0063; s.e. = 0.0795. $$

Remark 2.3

In the above and in many such similar contexts, use of stack of cards of different colors can be conveniently replaced by use of spinner wheels marked with different colors in different parts. Thus, for example, red color may occupy 40 percent of the area in the wheel. Naturally, we are referring to the back side of the wheel for coloring purposes. This should be understood, and we will not dwell with this version of the randomization.

2.3 Generalizations of RRMs

We now introduce several generalizations of the above RRMs—these are dictated by real-life applications. Always, the idea is to provide increased and perceived protection to the respondents from the perspective of protecting their confidentiality. In RRM2, we replaced $\bar{Q}$ by a completely simple-minded question which had nothing to do with the stigmatizing question Q. It was at times felt that this might still throw some doubt in the minds of the respondents. It is advisable that we utilize a question in the Set II which is not too far removed from Q which was taken to be false claims for social benefits. What about using ‘My family makes 2 or more out-of-state trips on an average every year’ whose affirmative version we may denote by $Q^{*}$ while the negation is denoted by $\bar{Q}^{*}$? This may not be totally stigmatizing in nature, and the respondents may not feel like either abstaining or giving a wrong answer if a card from Set II is actually selected in the randomization process. However, the true proportion of respondents (in the population as a whole) belonging to the category of $Q^{*}$ may not be known beforehand. That simply means that this time f will still follow binomial distribution with parameters $(n, \eta )$ where $\eta = p P + (1 - p) P^{*}$ where $P^{*}$ stands for the chance of $Q^{*}$, the affirmative version of the choice placed in the cards of Set II. Therefore, we may still develop the defining equation $f/n = pP +(1-p)P^{*}$. Whereas in the cases of RRM1 and RRM2, in this kind of equation, P was the only unknown proportion to be estimated, this time we have two unknowns, viz., P and $P^{*}$. Therefore, we need one more equation involving these two unknown parameters. This calls for the following RRM3.

We divide the whole collection of respondents into two equal/almost equal groups, say of sizes n1 and n2. For Group I, we collect information by using a version of RRM2, viz., by replacing the question related to birth by the question related to $Q^{*}$ on family trips. This results in the pair $(f1, n1)$ upon implementation. For notational simplicity and for ease of making generalizations, we use p1 for p. Therefore, f1 is distributed as binomial $(n1, \eta 1$ where $\eta 1 = p1P + (1 - p1)P^{*}$. Likewise, for Group II, based on the data of the form $(f2, n2)$, from the cards drawn from Set II, it turns out that f2 is binomial with parameters $(n2, \eta 2)$ where $\eta 2 = p2P + (1 - p2)P^{*}$. Note that $\eta 1$ and $\eta 2$ are, respectively, the proportions of cards in the two Sets I and II bearing the affirmative versions of Q and $Q^{*}$, respectively.

We have generated two equations, viz.,

$$ f1/n1 = \eta 1 = p1P + (1 - p1)P^{*}: f2/n2 = \eta 2 = p2P + (1 - p2)P^{*}. $$

From the above, we may easily solve the primary parameter P [as well as the other parameter $P^{*}$].

The solutions are linear functions of the sample proportions f1 / n1 and f2 / n2. Therefore, we can work out variance estimates and estimated variances in a routine manner. It must be noted that the solutions exist only when our choice is such that $p1 \ne p2$.

Illustrative Example 2.3

We choose $n1 = n2 = 120$ and $p1 = 0.40~{\text {and}}~p2 = 0.60$. Suppose survey yields $f1 = 57~\text {and}~f2 = 75$. This leads to the equations:

$$ 57/120 = 0.40P + 0.60P^{*}; 75/120 = 0.60P + 0.40P^{*}. $$

Therefore, the estimates for P and $P^{*}$ are 0.925 and 0.175, respectively. Before proceeding further with other approaches/methods, we will digress for a moment to discuss a source of non-response and its follow-up studies.

2.4 Not-at-Homes: Source of Non-response

While extracting information through a direct response survey on some features [qualitative or quantitative] from the respondents in a survey population, it is generally believed that there would be cooperation from the respondents—at least when the features are non-sensitive in nature. Of course, for sensitive features, we need to develop RRTs. However, there are instances where we encounter non-response for various reasons even when the features are non-evasive in nature. One of such sources is attributed to ‘Not-at-homes.’ Survey sampling researchers attempted to study this phenomenon. Notable contributors are: Yates (1946), Hansen and Hurwitz (1946), Hartley (1946), Politz and Simmons (1949), and Deming (1953). Their studies were essentially geared toward regular features of the survey questions. The technique for extraction of ‘response’ is known as Hartley–Politz–Simmons technique.

Much later, Rao (2014) considered the case of handling situations, wherein it is unlikely for a respondent to reveal truthful answer(s) even when it is non-sensitive in nature. It was followed up by yet another follow-up paper by Rao et al. (2016). We will not elaborate on this issue further.

2.5 RRMs—Further Generalizations

Following Blair et al. (2015), we will now briefly discuss two more generalizations of the basic RRM.

• (i) Forced Response Designs [FRD]: This RRM incorporates a forced response of yes as well as a forced response of no. The idea is to label forced yes (no) to the outcome 1(6), while for any other outcome of the throw of a regular [unbiased] six-faced die the respondent is supposed to give truthful response in terms of yes/no for possession of the sensitive stigmatizing feature. Thus eventually, we have only yes or no response from each respondent.

• (ii) Disguised Response Design [DRD]: The yes response to the sensitive feature is meant to be identified as the YES Stack of black and red cards. Likewise, the no response to the sensitive feature is to be identified as the NO Stack of black and red cards. Total number of cards is the same for both types of stacks. Further, if we have 80 percent red cards in YES Stack, then we must have 20 percent red cards in the NO Stack. This may be arbitrary but must be predetermined and be the same for all respondents. Every respondent is supposed to truthfully implement his choice of the correct stack by referring to the sensitive stigmatizing feature under study. Once this is done, he/she is supposed to draw a card at random from the correctly selected stack and only disclose the color of the card drawn—without any mention of the stack identified. Whether the respondent belongs to yes/no category [in respect of the feature under study] is his/her truthful confession to himself/herself.

Illustrative Example 2.4

Here, we discuss about FRD. We take $n = 300$, and suppose after implementation of the FRD, we obtain: yes count $=$ 180 and no count $=$ 120. Let P be the true proportion of persons possessing the sensitive feature in the population. Then, the chance of yes response from a respondent is given by $1/6 + 4P/6$ and we equate this to the sample proportion $=$ 180 / 300. This yields $\hat{P}=0.65$. Further, it can be shown that

$$ {\hat{V}}(\hat{P}) = 9[f(n - f)/n^2 (n - 1)]/4 = 0.0018, $$

upon simplification. Hence, s.e. of the estimate $=$ 0.0424.

Illustrative Example 2.5

We take up DRD now. We start with $n = 300$ respondents, and suppose, upon implementation of the DRD, we obtain: red count $=$ 180 and black count $=$ 120. Let P be the true proportion of persons possessing the sensitive feature in the population. Then, the chance of red card being drawn is given by $0.8P + 0.2(1 - P) = 0.2 + 0.6P$. We equate this to the sample proportion $=$ 180 / 300. This yields ${\hat{P}}= 0.6667$. Further,

$$ {\hat{V}}({\hat{P}}) = 25[f(n - f)/n^2 (n - 1)]/9 = 0.0021, $$

upon simplification. Hence, s.e. of the estimate 0.0458.

2.6 RRMs for Two Independent Stigmatizing Features

In case there are two or more sensitive qualitative features of a population to be studied, one can always study them separately. However, a joint study makes more sense since less effort will be spent to capture incidence. The RRM2 discussed above can be conveniently generalized to cover this situation. In the deck of cards, we accommodate cards of three different colors: black, red, and yellow. Black [red/yellow] cards read: Answer Q1 [Q2/Q3] truthfully where Q1 refers to SQlF1: underreporting income tax returns; Q2 refers to SQlF2: false claims for social benefits; and Q3 refers to a simple-minded innocent statement like on an average my family makes 2 or more out-of-state trips per year. All the three questions seek truthful binary response: yes/no. We presume that apart from the unknown proportions P1, P2 referring to chances of underreporting of IT returns and making false claims for social benefits, respectively, the other parameter P3 referring to asserting the statement about family trips is also unknown [and, may be incidentally estimated]. Thus, we are in the framework of three unknown parameters, and hence, we need three different [technically called linearly independent] estimating equations. We proceed by dividing the total number of respondents into three equal/almost equal groups. Also, we need three sets of cards with three different proportions of color compositions.

Illustrative Example 2.6

We start with $n = 301, n1 = n2 = 100, n3 = 101$. Further, color distribution of the cards in the three sets is taken as

Set I : B : R : Y : : 25, 30, and 45 percents;

Set II : B : R : Y : : 30, 45, and 25 percents;

Set III : B : R : Y : : 45, 25, and 30 percents.

Each respondent from Group I will pick up a card at random from Set I and will only communicate the truthful answer: yes/no—without divulging the color of the card drawn. Likewise, for respondents from the other two groups, same conditions apply. Suppose the proportions of yes answers are: 55/100, 43/100, and 51/101. Then, the defining equations are:

$$ 0.55 = 0.25P1+0.30P2+0.45P3; 0.43 = 0.30P1+0.45P2+0.25P3; $$

$$ 0.52 = 0.45P1+0.25P2+0.0.30P3. $$

From the above, we derive the estimates as

$$ {\hat{P}}1= 0.5155; {\hat{P}}2 = 0.1454; {\hat{P}}3 = 0.8385. $$

Remark 2.4

In the above example, it is tacitly assumed that the two sensitive features are independently distributed over the reference population. Otherwise, the two should be jointly studied in terms of $2 \times 2$ classification: [(Yes, Yes), (Yes, No), (No, Yes), (No, No)]. This and much more are discussed in the published literature. See, for example, Hedayat and Sinha (1991).

2.7 Toward Perception of Increased Protection of Confidentiality

Since the introduction of RRT, survey sampling practitioners/theoreticians have paid due attention to this area of survey methodological research. As has been mentioned, the purpose is to be able to elicit a truthful response on sensitive feature(s) from the sampled respondents, so that eventually the population proportion of incidence of the sensitive feature can be unbiasedly estimated. Toward this, a novel technique was introduced by Raghavarao and Federer (1979) and it was termed block total response [BTR] technique. A precursor to this study was undertaken by Smith et al. (1974). We propose to discuss the basic BTR technique with an illustrative example.

As usual, we start with one SQlF, say Q [with an unknown incidence proportion P to be estimated from the survey] and along with it we also consider a collection of 8 RQlFs $[Q1, Q2, \ldots , Q8]$ which are simple-minded and yet binary response queries. We thus have a total collection of nine QlFs, including the SQlF. The steps to be followed are:

• (i) We prepare several blocks of questions, i.e., a questionnaire involving, say some 4 of the RQlFs and the SQlF in each block. The only condition to be satisfied in the formation of the blocks is that each RQlF must appear the same number of times in the entire collection of blocks. Additionally, we also prepare a Master Block $Bl^{*}: [Q1, Q2, \ldots , Q8]$ comprising of all the RQlFs.

  For example, we may choose

  $$ Bl~1 : [Q1, Q2, Q4, Q6; Q]; Bl~ 2 : [Q1, Q3, Q6, Q7; Q], $$
  $$ Bl~3 : [Q2, Q3, Q5, Q8; Q]; Bl~ 4 : [Q4, Q5, Q7, Q8; Q]. $$

• (ii) Since we have a total of five blocks, we need five groups of respondents. The first four groups for dealing with blocks $Bl~1 - Bl~4$ are assumed to have the same size, say 50 each. In addition, we will go for some 30 respondents, for example, for the block $Bl^{*}$. So, we are dealing with a collection of say 230 respondents—randomly divided into these five groups.

• (iii) Each member of the first group of respondents is exposed to the questions contained in Bl 1, and he/she is told to respond truthfully to each of the RQlFs as also to the Q. However, he/she is supposed to report/divulge only the block total response [BTR]—the total score in terms of yes responses. This is continued for all other blocks as also for the Master Block $Bl^{*}$.

• (iv) The above completes the survey aspect of the BTR technique. Suppose we end up with the following summary data in terms of average score in each block per respondent:

  $$ Bl~1 : 0.285; Bl~2 : 0.354; Bl~3 : 0.328; Bl~4 : 0.396; Bl^{*}~: 0.395. $$

• (v) An estimate of the incidence proportion P of the SQlF is given by the computational formula:

  • (a) Sum of average scores in the first four blocks $=$ 1.363, and this is equated to $[2\sum Pi + 4P]/5$.

  • (b) The average score of 0.395 in the last block is equated to $\sum Pi$/8.

  • (c) From the above, ${\hat{P}} = [5 \times 1.363 - 2 \times 8 \times 0.395]/4 = 0.324$.

Remark 2.5

The above illustration arises out of a very general approach toward BTR technique. Naturally, once a respondent is told to provide only the BTR without divulging any kind of details as to the nature of individual responses, the investigator may be assured of increased cooperation from the respondents. This basic BTR technique has been extended further with an aim to provide enhanced protection of privacy to the respondents. The details may be found in Nandy et al. (2016) and Sinha (2017).

2.8 Confidentiality Protection in the Study of Quantitative Features

Consider a situation wherein we are dealing with a finite [labeled] population of size N and there is a sensitive qualitative study variable Y for which the ‘true’ values are $Y_1, Y_2, \ldots , Y_N$ for the units in their respective orders. To start with, these values are unknown and we want to unbiasedly estimate the finite population mean $\bar{Y}=\sum _i Y_i/N$.

We may adopt SRSWOR(N, n) or any other suitably defined fixed size (n) sampling design and draw a random sample of n respondents. Had the study variable been non-sensitive in nature, we could take recourse to ‘direct questioning’ involving the sampled respondents. In a very general setup, we may make use of the Horvitz–Thompson estimate [HTE, for short]. It simplifies $\bar{y}$ when SRSWOR(N, n) is adopted. However, we are dealing with a sensitive characteristic [such as ‘income accrued through illegal profession’] and we need to use a suitably defined RRT. Here, we propose an RRT for this purpose.

Assume that the true Y-values are completely covered by a pool of K known quantities like $M_1, M_2, \ldots , M_K$. The set of M-values may even comprise a larger set. Therefore, in effect, we are assuming that the N population values are discrete in nature.

We choose a small fraction $\delta$ and proceed to deploy RRT as is explained in the following example with $K=10$ and $\delta =0.2$.

We prepare 25 identical cards, and at the back of the cards we give instructions: For each of five cards, it reads at the back: ‘Report your true income accrued through illegal profession.’ For the rest of the 20 cards, we use them in pairs, and for the ith pair, it reads at the back of both the cards: ‘Report $M_i{\text {'}}; i=1, 2, \ldots , 10$.

Each respondent chooses a card at random out of the 25 cards, reads out the back side, and acts accordingly. We assume that the respondents act honestly and provide ‘truthful’ figure—no matter which card is chosen—without disclosing in any way the nature of the card.

Note that the chance of choosing a card with marking as ‘Report your true income$\ldots$’ is $5/25=0.20$ which coincides with the chosen value of $\delta$. On the other hand, chance of picking up a card corresponding to any specified value $M_i$ is $2/25=0.08$ which is equal to $(1-\delta )/K$.

Using the notations $\delta$ and K, for the chosen sample of n respondents, we have thus collected the responses to be denoted by $R_1, R_2, \ldots , R_n$. Each response is random in nature and

$$\begin{aligned} E(R_i)=\delta Y_i + (1-\delta )\bar{M} \end{aligned}$$

(2.8.1)

where $\bar{M}=\sum _i M_i/K$ and $Y_i$ is the true [unknown] response of the ith sampled respondent. From this, it follows that $Y_i$ can be unbiasedly estimated as

$$\begin{aligned} {\hat{Y}}_i=[R_i - (1-\delta )\bar{M}]/\delta . \end{aligned}$$

(2.8.2)

Hence, an unbiased estimate for the finite population mean, based on estimates of $Y_i$’s, is obtained by referring to HTE in general and to the sample mean of estimated Y’s in case SRSWOR has been implemented during sample selection. The proof of this claim rests on the formula: $E=E_1E_2$. Therefore,

$$\begin{aligned} \hat{\bar{Y}}=\sum _i \hat{Y}_i/n. \end{aligned}$$

(2.8.3)

In the above, for $K=10$ and $\delta =0.2$, $\hat{Y}_i =[5 R_i - 4 \bar{M}]$ and hence $\hat{\bar{Y}}=5 \bar{R} - 4 \bar{M}$ is the estimate of population mean, under SRSWOR sampling. Here, $\bar{R}$ refers to the sample mean of the sampled R’s and $\bar{M}$ refers to the mean of the given M’s.

Remark 2.6

It may be noted that in the above it is tacitly assumed that each $Y_i$ matches with one of the given values $M_i$’s. However, no sampled respondent is supposed to divulge which M-value matched his/her true value of Y.

Below, we proceed to work out a formula for the estimated standard error [s.e.] of the estimate of the population mean based on the above procedure. In addition to $E(R_i)$ displayed in (2.8.1), we have

$$\begin{aligned} E(R^2_i)=\delta Y^2_i + (1-\delta ) \bar{Q}_M \end{aligned}$$

(2.8.4)

where $\bar{Q}_M=\sum _i M^2_i / K$ is the mean of squares of the M-values.

These suggest

$$\begin{aligned} V(R_i)= \delta (1-\delta )Y^2_i + (1-\delta )[\bar{Q}_M - (1-\delta )\bar{M}^2] - 2 \delta (1-\delta )Y_i \bar{M}. \end{aligned}$$

(2.8.5)

From (2.8.4), it follows that

$$\begin{aligned} {\hat{Y}}^2_i=[R^2_i - (1-\delta )\bar{Q}_M]/\delta \end{aligned}$$

(2.8.6)

Using (2.8.6), we may deduce that

$$\begin{aligned} {\hat{V}}(R_i)&=(1-\delta )[R^2_i -(1-\delta )\bar{Q}_M] + \nonumber \\&{\qquad } (1-\delta )[\bar{Q}_M-(1-\delta )\bar{M}^2] - 2(1-\delta ) \bar{M}[R_i - (1-\delta )\bar{M}] \end{aligned}$$

(2.8.7)

which simplifies to

$$\begin{aligned} (1-\delta ) [R_i - \bar{M}]^2 + \delta (1-\delta )[\bar{Q}_M -\bar{M}^2] \end{aligned}$$

(2.8.8)

We now proceed to work out estimated standard error for the estimate of the finite population mean under SRSWOR(N, n). Clearly, under SRSWOR(N, n),

$$\begin{aligned} \hat{\bar{Y}}= \sum _i \hat{Y}_i / n; \hat{Y}_i=[R_i- \bar{M}(1-\delta )]/\delta \end{aligned}$$

(2.8.9)

Moreover,

$$\begin{aligned} V[{\hat{\bar{Y}}}]=V_1E_2 + E_1V_2 \end{aligned}$$

(2.8.10)

Note that

$$\begin{aligned} V_1E_2=V_1\left( \sum _i Y_i/n\right) =(1/n - 1/N) S^2_Y \end{aligned}$$

(2.8.11)

where $S^2_Y$ refers to the population variance of Y-values with divisor $N-1$. To estimate this, we usually employ the sample counterpart of $S^2_Y$, viz., $s^2_Y=sum_i (Y_i - \bar{Y})^2/(n-1)$. Here, of course, $Y_i$’s are unknown and are being estimated in terms of the R’s by an application of RRT. The expression for $s^2_Y$ involves square terms, i.e., $Y^2_i$’s and cross-product terms, i.e., $Y_iY_j$’s. From (2.8.6), we deduce expressions for $\hat{Y}^2_i$’s. Since the respondents act independently, estimates of the product terms $Y_iY_j$’s are also derived by the product of terms of the form (2.8.4). This takes care of estimate for $V_1E_2$ term.

Next, note that for every sampled respondent such as the ith, $V_2$ refers to variance of $\hat{Y}_i$. From (2.8.4), it follows that $V(\hat{Y}_i)=V(R_i)/\delta ^2$. From (2.8.7), we readily have an expression for estimate of $V(R_i)$. Therefore,

$$\begin{aligned} {\hat{E}}_1V_2=\sum _i {\hat{V}}({\hat{Y}}_i)/n^2=\sum _i {\hat{V}}(R_\mathbf i )/n^2\delta ^2 \end{aligned}$$

(2.8.12)

Illustrative Example 2.7

As before, we take $K=10$ and $\delta =0.2$. Let our choice of M’s be [expressed in units of thousand rupees]: $1, 2, \ldots , 10$. We consider a small population and adopt $SRSWOR(N=20, n=5)$. Let the sampled R’s [as per the respondents’ reporting] be: 3, 7, 4, 8, 5, that is our data. We show the necessary computations below.

From (2.8.4), we obtain an estimate of the population mean of Y-values as the sample mean computed as Rs. $25/5=5$ thousand. To compute estimated s.e. of the estimate, we proceed as follows:

From the discussion below (2.8.11), it follows that an estimate of $V_1E_2$ is given by $(1/n - 1/N)$ times an unbiased estimate of $s^2_Y$ based on the computations in Example 2.7 above. Since $s^2_Y=[(n-1)\sum _i Y^2_i - \sum \sum _{i ne j} Y_i Y_j]/n(n-1)]$, we do term by term estimation by using relevant square terms and product terms from Example 2.7. This yields:

$\hat{s^2_Y} = [4 \times 45 - 80]/20= 5$ and hence, an unbiased estimate of $V_1E_2$ is given by $(1/5 - 1/20) \times 5=3/4=0.75.$

For the other term, viz., $E_1V_2$, an unbiased estimate is to be computed from (2.8.12) in combination with (2.8.7). For the computations, note that $\bar{Q}_M = 38.5$. In (2.8.7),

Term 1[with positive sign]:

$$ {\hat{V}}(R_i)=(1-\delta )[R^2_i -(1-\delta )\bar{Q}_M] = 0.8 [R^2_i - 30.8] $$

Term 2 [with positive sign]:

$$ (1-\delta )[\bar{Q}_M-(1-\delta )\bar{M}^2] =14.3 $$

Term 3 [with negative sign]

$$2(1-\delta )\bar{M}[R_i - (1-\delta )\bar{M}]=8.8 [R_i - 4.4]$$

Therefore, unbiased estimate of $E_1V_2$ is computed as $[7.20 + 71.50 - 44.00]/16= 34.70$. Finally, adding the two components, an unbiased estimate of the variance $=$ $0.75 + 34.70=35.45$ so that estimated $s.e.=\sqrt{(}35.45)=5.95$.

Remark 2.7

In a similar study, Bose (2015) took up the case of SRSWR(N, n) and derived expression for the estimate of the population mean and an expression for its variance. The above study is quite general in nature and applies to any fixed size (n) sampling design.

Remark 2.8

The BTR technique discussed in the context of sensitive qualitative feature can be extended to the case of sensitive quantitative feature—without the assumption of ‘closure’ w.r.t. a given set of known quantities such as $[M_1, M_2, \ldots , M_K]$. This has been taken up recently in Nandy and Sinha (2018). We omit the details.

2.9 Concluding Remarks

The topic of RRT is vast and varied in terms of the published literature in the form of papers, books, and reports. We have simply introduced the basic ideas and initial methodologies that were suggested in the context of estimation of a population proportion of a sensitive feature of the members of a population. We have also presented one method w.r.t. quantitative feature. There are similar methodologies dealing with (i) more than one sensitive qualitative features, (ii) one or more sensitive quantitative features, and so on.