Discrete Legendre Collocation Methods for Fredholm–Hammerstein Integral Equations with Weakly Singular Kernel

Abstract

In this paper, we discuss the discrete Legendre collocation methods for Fredholm–Hammerstein integral equations with the weakly singular kernel. Using sufficiently accurate quadrature rule, we obtain the convergence rates for the discrete Legendre collocation solutions to the actual solution in both $L^2$ and infinity norm. Numerical examples are presented to validate the theoretical estimates.

1 Introduction

We consider the following Fredholm–Hammerstein integral equation

$$\begin{aligned} u(s)-\int _{-1}^1 k(s,t)\,\psi (t, u(t))\,\mathrm{d}t=f(s),\,\,\, -1\le s\le 1, \end{aligned}$$

(1)

where k, f and $\psi$ are known functions, u is the unknown function to be determined in a Banach space $\mathbb {X}$, and the kernel k(., .) is of weakly singular type of the form

$$\begin{aligned} k(s, t)=m(s, t)g_{\alpha }|s-t|, \end{aligned}$$

$m(s, t)\in \mathcal{C}([-1, 1]\times [-1, 1])$ and

$$\begin{aligned} g_{\alpha }(x)=\left\{ \begin{array}{l@{}l} {x^{\alpha -1}},~~~~~~~~~\text{ if }\;\;1/2<\alpha <1, \\ {\log x, ~~~~~~~~~\text{ if }\;\;\alpha =1}. \end{array}\right. \end{aligned}$$

This type of problem (1) arises as a reformulation of boundary value problems with certain nonlinear boundary conditions.

Many authors have studied numerical methods to solve nonlinear integral equations with the smooth kernel and also with weakly singular kernel [7,8,9,10,11, 13]. The Galerkin, collocation, Petrov–Galerkin degenerate kernel methods, and Nystr${\ddot{\mathrm{o}}}$m methods are commonly used projection methods for finding the numerical solution of Eq. (1). In all the projection methods, the infinite dimensional space $\mathbb {X}$ is approximated by the space of piecewise polynomials. However, to get better accuracy in piecewise polynomial-based projection methods, one has to solve a large system of nonlinear equations because of a large number of the partition. So, in the last some years, different spectral methods have been developed rapidly and the Legendre spectral methods have been applied to linear integral equations and nonlinear integral equations. The Legendre spectral projection methods for Fredholm–Hammerstein integral equations with smooth kernel have been studied in [4]. The important point is if $\mathcal{P}_n$ denotes either orthogonal or interpolatory projection from $\mathbb {X}$ into a subspace of global polynomials of degree $\le n$, then $\Vert \mathcal{P}_n\Vert _{\infty }$ is unbounded. In [4], the similar convergence rates for the approximate solution of Fredholm–Hammerstein integral equations with smooth kernel have been obtained in both $L^2$ and infinity norm as in the case of piecewise polynomial bases.

However, the spectral projection methods lead to the algebraic nonlinear system, in which the coefficients are integrals appeared due to inner products and integral operator $\mathcal{K}$. Since these integrals are almost always evaluated numerically, in all the above methods the effect of error due to numerical integration has been ignored. So in the discrete methods, the integrals appeared in the nonlinear system of equations have been replaced by numerical quadrature rule. The discrete spectral methods for nonlinear integral equations have been discussed by [5]. However, in all these above methods, the nonlinear integral equations with smooth kernel have been considered. The integral equations with weakly singular kernels of the algebraic and logarithmic type cover many important applications, and this kind of problem arises from potential problems, Dirichlet problems, the description of the hydrodynamic interaction between elements of a polymer chain in solution, mathematical problems of radiative equilibrium, and transport problems.

In this paper, we apply the discrete Legendre spectral collocation methods to solve the Fredholm–Hammerstein integral equations with the weakly singular kernel. Our purpose in this paper is to obtain similar convergence rates as in using piecewise and global polynomial bases for smooth kernels.

The organization of this paper is as follows. In Sect. 2, we discuss the discrete Legendre collocation methods for Hammerstein integral equations with the weakly singular kernel. In Sect. 3, we discuss the convergence rates for both $L^2$ and infinity norm. In Sect. 4, we illustrate our result by the numerical example. Throughout this paper, we assume c is a generic constant.

2 Hammerstein Integral Equations

In this section, we will discuss on the collocation methods for solving Hammerstein integral equations with weakly singular kernels (1) using Legendre polynomial basis functions.

Let $\mathbb {X}=\mathcal{C}[-1,1]$ and $L^2[-1,1]$ with norms $\Vert .\Vert _{\infty }$ and $\Vert .\Vert _{L^2}$, respectively. Throughout the paper, the following assumptions are made on f, k(., .) and $\psi (.,u(.))$:

• (i) $f\in \mathcal {C}[-1,1]$.

• (ii) For $m(s, t)\in \mathcal{C}^{r}([-1, 1]\times [-1, 1])$, $r\ge 1$,

  $$\begin{aligned}&\Vert m\Vert _{\infty }=\sup _{s,t\in [-1, 1]}|m(s, t)|\le M<\infty ,\\&\Vert m\Vert _{r, \infty }=\max _{0\le i, j\le r, t,s\in [-1, 1]}\Big |\frac{\partial ^{i+j}}{\partial s^i \partial t^j} m(s, t)\Big |. \end{aligned}$$

• (iii) For $s,s'\in [-1,1]$, $\displaystyle \Vert g_{\alpha }|s-t|-g_{\alpha }|s'-t|\Vert _{L^2}\rightarrow 0$ and $\Vert m_s(.)-m_{s'}(.)\Vert _{L^2} \rightarrow 0$ as $s\rightarrow s'$.

• (iv) For $1/2<\alpha <1$, $\displaystyle \sup _{s\in [-1, 1]}\int _{-1}^1 |g_\alpha |s-t||^2 \; \mathrm{d} t =M_2<\infty$.

• (v) The nonlinear function $\psi (t, u)$ is bounded and continuous over $[-1, 1]\times \mathbb {R}$. $\psi (t, u)$ is Lipschitz continuous in u, i.e., for any $u_1, u_2\in \mathbb {R}$, $\exists \, c_1>0$ such that

  $$|\psi (t, u_1)-\psi (t, u_2)|\le c_1 |u_1-u_2|,\,\, \forall \, t\in [-1,1].$$

• (vi) The partial derivative $\psi ^{(0,1)}(t, u(t))$ of $\psi$ with respect to the second variable exists and is Lipschitz continuous in u, i.e., for any $u_1, u_2\in \mathbb {R}$, $\exists \,c_2>0$ such that

  $$|\psi ^{(0, 1)}(t, u_1)-\psi ^{(0, 1)}(t, u_2)|\le c_2 |u_1-u_2|,\,\,\,\forall \, t\in [-1,1].$$

  This implies, $\psi ^{(0,1)}(., .)\in \mathcal{C}[-1,1]\times \mathbb {R}$, $\Vert \psi ^{(0,1)}\Vert _{\infty }\le B$.

• (vii) We assume that M, $M_2$, and $c_1$ satisfy the condition that $\sqrt{2M_2}Mc_1<1$.

Define

$$\begin{aligned} z(t)=\psi (t, u(t)),\,\,\,t\in [-1,1]. \end{aligned}$$

(2)

It is easy to show by using chain rule for higher derivatives that $z\in \mathcal{C}^{r}[-1, 1]$, because $\psi (., .)\in \mathcal{C}^{r}([-1,1]\times \mathbb {R})$ and $u\in \mathcal{C}^{r}[-1, 1]$.

Then, the Hammerstein integral equation (1) can be written as an operator form

$$\begin{aligned} u=\mathcal{K}z+f, \end{aligned}$$

(3)

where

$$\begin{aligned} \mathcal{K}z(s)=\int _{-1}^1 k(s, t)z(t)\, \mathrm{d}t. \end{aligned}$$

(4)

For our convenience, we consider a nonlinear operator $\varPsi :\mathbb {X}\rightarrow \mathbb {X}$ defined by

$$\varPsi (u)(t)=\psi (t, u(t)).$$

Then, Eq. (2) becomes

$$\begin{aligned} z=\varPsi (\mathcal{K}z+f). \end{aligned}$$

(5)

Let $\mathcal{T}(u)=\varPsi (\mathcal{K}u+f),$ $u\in \mathbb {X}$, then the Eq. (5) can be written as

$$\begin{aligned} \mathcal {T}z=z. \end{aligned}$$

(6)

Now, we will prove the existence and uniqueness of the solution of Eq. (6) in the next theorem.

Theorem 1

Let $\mathbb {X}=\mathcal{C}[-1,1]$, $f\in \mathbb {X}$ and $g_{\alpha }|s-t|$ satisfy the assumption (iv) with $m(.,.)\in \mathcal{C}[-1,1]\times [-1,1]$. Let $\psi (t, u(t))\in \mathcal{C}([-1,1]\times \mathbb {R})$ satisfy the Lipschitz condition in the second variable and $\sqrt{2M_2}Mc_1<1$. Then, the operator equation $\mathcal{T}z=z$ has a unique solution $z_0\in \mathbb {X}$, i.e., $z_0=\mathcal{T}z_0$. $\square$

Proof

Using Cauchy–Schwarz inequality, we get

$$\begin{aligned} \Vert \mathcal{K}z\Vert _{\infty }=\sup _{s\in [-1, 1]}|\mathcal{K}z(s)|\le & {} \sup _{t, s\in [-1, 1]}|m(s, t)|\sup _{s\in [-1, 1]}\int _{-1}^1 |g_{\alpha }|s-t|z(t)|\,\mathrm{d}t\nonumber \\\le & {} M\sqrt{M_2}\Vert z\Vert _{L^2}. \end{aligned}$$

(7)

Since $f\in \mathcal{C}[-1, 1]$, it follows that $u=\mathcal{K}z+f\in \mathcal{C}[-1, 1]$. Let $z_1, z_2\in \mathcal{C}[-1,1]$. Using the Lipschitz continuity of $\psi (., u(.))$ with Eq. (7), we get

$$\begin{aligned} \Vert \mathcal {T}z_1 -\mathcal {T}z_2\Vert _{\infty }= & {} \Vert \varPsi (\mathcal{K}z_1+f)-\varPsi (\mathcal{K}z_2+f)\Vert _{\infty }\nonumber \\\le & {} c_1\Vert \mathcal{K}(z_1-z_2)\Vert _{\infty }\nonumber \\\le & {} c_1M\sqrt{M_2}\Vert z_1-z_2\Vert _{L^2}\le \sqrt{2M_2}c_1M\Vert z_1-z_2\Vert _{\infty }. \end{aligned}$$

(8)

By assumption (vii), $\sqrt{2M_2}Mc_1<1$, hence $\mathcal{T}$ is a contraction mapping on $\mathbb {X}$. By using Banach contraction theorem, $\mathcal{T}$ has a unique fixed point in $\mathbb {X}$. Denote the unique solution as $z_0$. This completes the proof. $\square$

To describe Legendre collocation methods for the solution of Hammerstein integral equation (1), we will first approximate the space $\mathbb {X}$ by a finite-dimensional space $\mathbb {X}_n$. Let $\mathbb {X}_n$ be the set of all polynomials of degree not more than n. Let $\{\tau _0, \tau _1,\dots , \tau _n\}$ be the zeros of the Legendre polynomial of degree $n+1$. For $z\in \mathcal{C}[-1, 1]$, we define the Lagrange interpolation polynomial $\mathcal{Q}_n:\mathbb {X}\rightarrow \mathbb {X}_n$ by

$$\begin{aligned} \mathcal{Q}_n z(s)=\sum _{i=0}^n z(\tau _i)L_i(s),\,\, s\in [-1, 1] \end{aligned}$$

where

$$L_i(s)=\frac{\pi (s)}{(s-\tau _i)\pi '(\tau _i)},\,\,\,\pi (s)=(s-\tau _0)(s-\tau _1)\dots (s-\tau _n).$$

Then, $\mathcal{Q}_n:\mathbb {X}\rightarrow \mathbb {X}_n$ satisfies

$$\begin{aligned} \mathcal{Q}_nu\in \mathbb {X}_n, \,\,\,\,\mathcal{Q}_nu(\tau _i)=u(\tau _i),\,\,i=0,1,\dots ,n,\,\,u\in \mathbb {X}. \end{aligned}$$

(9)

We quote the following lemma from [3, 6], which gives the properties of the interpolatory projection operator $\mathcal{Q}_n$.

Lemma 1

Let $\mathcal{Q}_n:\mathbb {X}\rightarrow \mathbb {X}_n$ be the interpolatory projection operator defined by (9). Then, the following hold:

(i):

$\{\mathcal{Q}_n: n\in \mathbb {N}\}$ is uniformly bounded in $L^2$ norm, that is, $\Vert \mathcal{Q}_n u\Vert _{L^2}\le p\Vert u\Vert _{\infty },\,\,u\in \mathcal {C}[-1,1],$ where p is a constant independent of n.

(ii):

For any $u\in \mathcal {C}^r[-1,1],$ there exists a constant c independent of n such that

$$\begin{aligned}&\Vert \mathcal{Q}_nu-u\Vert _{L^2}\le cn^{-r}\Vert u^{(r)}\Vert _{L^2}. \end{aligned}$$

Then, the Legendre collocation method for Eq. (5) is seeking an approximate solution $z_n(s)=\sum _{i=0}^n \gamma _i L_i(s)\in \mathbb {X}_n$, which satisfies the following nonlinear system of equations

$$\begin{aligned} \sum _{i=0}^n \gamma _i L_i(\tau _j)=\varPsi \Big (\mathcal{K}\Big (\sum _{i=0}^n \gamma _i L_i\Big )+f\Big )(\tau _j),\,\,j=0,1,\dots , n. \end{aligned}$$

Using the interpolatory projection operator, the above system of nonlinear equations can be written in the following operator equation form.

$$\begin{aligned} z_n=\mathcal{Q}_n\varPsi (\mathcal{K}z_n+f). \end{aligned}$$

(10)

Corresponding approximate solution $u_n$ of u is given by

$$\begin{aligned} u_n=\mathcal{K}z_n+f. \end{aligned}$$

Using the projection operator $\mathcal{Q}_n$, we define $\mathcal{K}_n: \mathbb {X}\rightarrow \mathbb {X}$ by

$$\begin{aligned} \mathcal{K}_n (z)(s)=\int _{-1}^1 g_{\alpha }|s-t|\mathcal{Q}_n(m(s, t)z(t))\,\mathrm{d}t, \end{aligned}$$

(11)

which approximates the operator $\mathcal{K}$. For $z_n\in \mathbb {X}_n$, we have

$$\begin{aligned} \mathcal{K}_n (z_n)(s)=\sum _{i=0}^n w^{\alpha }_i(s) m(s, \tau _i)z_n(\tau _i), \end{aligned}$$

where $\displaystyle w^{\alpha }_i(s)=\int _{-1}^1 L_i(s)g_{\alpha }|s-t|\,\mathrm{d}t$.

Denote $L^{(r)}_2[-1, 1]=\{u: D^i_s u\in L^2[-1, 1], i=0,1,\dots , r\}$ with the norm

$$\Vert u\Vert _{L^2, r}=\sum _{i=0}^r \Vert D^i_s u\Vert _{L^2}.$$

Now in the following Lemma, we give the error bounds of the integral operator $\mathcal {K}$ with the approximate operator $\mathcal {K}_n$.

Theorem 2

Let $m(s,t) \in \mathcal {C}^{(0, r)}([-1, 1] \times [-1, 1])$ and $z \in \mathcal {C}^r[-1, 1]$. Then, there exists a positive constant c such that

$$\begin{aligned} \Vert (\mathcal {K} -\mathcal {K}_n) z\Vert _{\infty } \le c n^{-r}\Vert z\Vert _{L^2, r} . \end{aligned}$$

(12)

Proof

For fixed $s\in [-1, 1]$, denote $b_s(t)=m_s(t)z(t)$, where $m_s(t)=m(s, t)$. From Eqs. (11) and (4), we obtain

$$\begin{aligned} |(\mathcal{K}-\mathcal{K}_n)z(s)|=\Big |\int _{-1}^1 g_{\alpha }|s-t| (\mathcal{I}-\mathcal{Q}_n)(m(s,t) z(t))\mathrm{d}t\Big |. \end{aligned}$$

Now by taking supremum over $s\in [-1, 1]$ and using Cauchy–Schwarz inequality with Lemma 1, we get

$$\begin{aligned} \Vert (\mathcal{K}-\mathcal{K}_n)z\Vert ^2_{\infty }\le & {} M_2\sup _{s\in [-1, 1]}\Vert (\mathcal{I}-\mathcal{Q}_n)b_s\Vert ^2_{L^2}\nonumber \\= & {} M_2n^{-2r}\sup _{s\in [-1, 1]} \Big (\int _{-1}^1 |[b_s(t)]^{(r)}|^2 \mathrm{d}t\Big ). \end{aligned}$$

(13)

Using Leibniz rule for differentiating the product of two terms and Cauchy–Schwarz inequality again, we get

$$\begin{aligned} \Big ([b_s(t)]^{(r)}\Big )^2= & {} \Big (\sum _{i=0}^r C^r_i\, D^{r-i}_t m(s, t)\, D^{i}_{t}z(t)\Big )^2\nonumber \\\le & {} \Vert D^{r-i}_t m_s\Vert _{\infty }^2 \Big (\sum _{i=0}^r (C^r_i)^2\Big ) \Big (\sum _{i=0}^r (D^{i}_{t}z)^2(t)\Big ) \end{aligned}$$

(14)

Using Eq. (14) in Eq. (13), we obtain

$$\begin{aligned} \Vert (\mathcal{K}-\mathcal{K}_n)z\Vert ^2_{\infty }\le & {} M_2n^{-2r}\Vert m\Vert ^2_{r, \infty }\Big (\sum _{i=0}^r (C^r_i)^2\Big ) \Big (\int _{-1}^1\sum _{i=0}^r (D^{i}_{t}z)^2(t)\mathrm{d}t\Big )\\\le & {} M_2n^{-2r}\Vert m\Vert ^2_{r, \infty }\Big (\sum _{i=0}^r (C^r_i)^2\Big )\Big (\sum _{i=0}^r\Vert D^i_t z\Vert ^2_{L^2}\Big )\\\le & {} M_2n^{-2r}\Vert m\Vert ^2_{r, \infty }\Big (\sum _{i=0}^r (C^r_i)^2\Big )\Vert z\Vert ^2_{L^2, r}. \end{aligned}$$

Thus, we get

$$\begin{aligned} \Vert (\mathcal{K}-\mathcal{K}_n)z\Vert _{\infty }\le \sqrt{M}_2n^{-r}\Vert m\Vert _{r, \infty }\Big (\sum _{i=0}^r (C^r_i)^2\Big )^{1/2}\Vert z\Vert _{L^2, r}\le cn^{-r}\Vert z\Vert _{L^2, r}. \end{aligned}$$

This completes the proof.

Now by using the approximate discrete operator $\mathcal{K}_n$ instead of the integral operator $\mathcal{K}$, we obtain

$$\begin{aligned} \sum _{i=0}^n \xi _i L_i(\tau _j)=\varPsi \Big (\mathcal{K}_n\Big (\sum _{i=0}^n \xi _i L_i\Big )+f\Big )(\tau _j),\,\,\,\,j=0,1,\dots , n. \end{aligned}$$

(15)

Then, $\displaystyle \tilde{z}_n(t)= \sum _{j=0}^n \xi _j L_j(t)$ is the discrete Legendre collocation approximate solution of z of Eq. (5).

Using the interpolation operator $\mathcal{Q}_n$, the system of nonlinear equations (15) can be written in the following operator equation forms.

$$\begin{aligned} \tilde{z}_n=\mathcal{Q}_n\varPsi (\mathcal{K}_n\tilde{z}_n+f). \end{aligned}$$

(16)

Let $\widetilde{{\mathcal{{T}}}}_n(u)=\mathcal{Q}_n\varPsi (\mathcal{K}_n u+f)$, $u\in \mathbb {X}$, and Eq. (16) can be written as

$$\begin{aligned} \tilde{z}_n=\widetilde{{\mathcal{{T}}}}_n\tilde{z}_n. \end{aligned}$$

(17)

The corresponding approximate solution $\tilde{u}_n$ of u is defined by $\tilde{u}_n=\mathcal{K}_n\tilde{z}_n+f$.

3 Convergence Rates

In this section, we will discuss convergence rates of approximated solutions with the exact solution of Fredholm–Hammerstein integral equations with weakly singular kernel, in both $L^2$ and infinity norm. To do this, we quote the following lemma.

Definition 1

[1] Let $\mathbb {X}$ be a Banach space and, $\mathcal {T}$ and $\mathcal {T}_{n}\in B(\mathbb {X})$. Then, $\{\mathcal {T}_{n}\}$ is said to be $\nu$-convergent to $\mathcal {T}$ if $\Vert \mathcal {T}_{n}\Vert \le c,\; \;\; \Vert (\mathcal {T}_{n}-\mathcal {T})\mathcal {T}\Vert \rightarrow 0,\;\; \Vert (\mathcal {T}_{n}-\mathcal {T})\mathcal {T}_{n}\Vert \rightarrow 0\;\;\text{ as }\;\; n\rightarrow \infty .$

Theorem 3

[2] Let $\mathbb {X}$ be a Banach space and $\mathcal{T}$, $\mathcal{T}_n\in \mathbb {BL(X)}$. If $\mathcal{T}_n$ is norm convergent to $\mathcal{T}$ or $\mathcal{T}_n$ is $\nu$-convergent to $\mathcal{T}$ and $(\mathcal{I}-\mathcal{T})^{-1}$ exists and bounded on $\mathbb {X}$, then $(\mathcal{I}-\mathcal{T}_n)^{-1}$ exists and uniformly bounded on $\mathbb {X}$ for sufficiently large n.

Theorem 4

Let $\mathcal{K}_n$ be the approximate integral operator defined by the Eq. (11), then the set of operators $\{\mathcal {K}_n: n=1, 2, 3,\dots \}$ is collectively compact.

Proof

To prove $\{\mathcal {K}_n: n=1, 2, 3,\dots \}$ is collectively compact, we need to show that the set $\displaystyle \bigcup _n \mathcal{K}_n(B)$ is a relatively compact set whenever $B\subset \mathbb {X}$ is bounded.

Let $S=\{\mathcal{K}_n(z): z\in B\}$, and B is a closed unit ball in $\mathcal{C}[-1, 1]\subset L^2[-1, 1]$. To prove $\{\mathcal{K}_n(z)\}$ is a compact operator, we have to show that S is uniformly bounded and equicontinuous.

We have

$$\begin{aligned} \mathcal{K}_n (z)(s)=\int _{-1}^1 g_{\alpha }|s-t|\mathcal{Q}_n(m(s, t)z(t))\,\mathrm{d}t, \end{aligned}$$

Now by using Cauchy–Schwarz inequality and taking supremum over $s\in [-1, 1]$, we obtain

$$\begin{aligned} \Vert \mathcal{K}_n (z)\Vert _{L^2}\le \sqrt{2}\Vert \mathcal{K}_n (z)\Vert _{\infty } \le \sqrt{2M_2} \Vert \mathcal{Q}_n(m(s, t)z(t))\Vert _{L^2} \le c\,p M\Vert z\Vert _{L^2}. \end{aligned}$$

(18)

Thus, $\mathcal{K}_n$ is uniformly bounded in $L^2$ norm. Now to show the equicontinuity, for any $s, s'\in [-1, 1]$, we obtain

$$\begin{aligned}&\mathcal{K}_n (z)(s)-\mathcal{K}_n (z)(s') \nonumber \\&\quad =\int _{-1}^1 \Big (g_{\alpha }|s-t|\mathcal{Q}_n(m(s, t)z(t))- g_{\alpha }|s'-t|\mathcal{Q}_n(m(s', t)z(t))\Big )\,\mathrm{d}t\nonumber \\&\quad \le \int _{-1}^1 \Big (g_{\alpha }|s-t|-g_{\alpha }|s'-t|\Big ) \mathcal{Q}_n(m(s,t)z(t))\mathrm{d}t\nonumber \\&\quad + \int _{-1}^1 g_{\alpha }|s'-t|\mathcal{Q}_n\Big (m(s,t)z(t)-m(s', t)z(t)\Big )\mathrm{d}t. \end{aligned}$$

By using Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} |\mathcal{K}_n (z)(s)-\mathcal{K}_n (z)(s')|&\le \Big (\int _{-1}^1 (g_{\alpha }|s-t|-g_{\alpha }|s'-t|)^2\mathrm{d}t\Big )^{1/2} \Vert \mathcal{Q}_n(m(s,t)z(t))\Vert _{L^2}\nonumber \\&\quad + M_2 p\Vert m(s,t)-m(s', t)\Vert _{L^2}\Vert z\Vert _{\infty }. \end{aligned}$$

Using assumption (iii) in the above equation, we get $|\mathcal{K}_n (z)(s)-\mathcal{K}_n (z)(s')|\rightarrow 0$ as $s\rightarrow s'$ and $n\rightarrow \infty$. Thus, $\{\mathcal{K}_n(z)\}$ is equicontinuous on $[-1, 1]$. By using Arzela–Ascoli theorem, we conclude that $\{\mathcal{K}_n\}$ is collectively compact. This completes the proof.

We quote the following theorem which gives us the condition under which the solvability of one equation leads to the solvability of other equation.

Theorem 5

[13] Let $\widehat{\mathcal{F}}$ and $\widetilde{{\mathcal{{F}}}}$ be continuous operators over an open set $\varOmega$ in a Banach space $\mathbb {X}$. Let the equation $x=\widetilde{{\mathcal{{F}}}}x$ has an isolated solution ${\tilde{x}}_0\in \varOmega$, and let the following conditions be satisfied.

• (a) The operator $\widehat{\mathcal{F}}$ is Frechet differentiable in some neighborhood of the point $\tilde{x}_0$, while the linear operator $\mathcal{I}-\widehat{\mathcal{F}}'({\tilde{x}}_0)$ is continuously invertible.

• (b) Suppose that for some $\delta >0$ and $0<q<1$, the following inequalities are valid (the number $\delta$ is assumed to be so small that the sphere $\Vert x-\tilde{x_0}\Vert \le \delta$ is contained within $\varOmega$).

$$\begin{aligned} \sup _{\Vert x-\tilde{x}_0\Vert \le \delta }\Vert (\mathcal{I}-\widehat{\mathcal{F}}'(\tilde{x}_0))^{-1}(\widehat{\mathcal{F}}'(x)-\widehat{\mathcal{F}}'(\tilde{x}_0))\Vert \le q,\end{aligned}$$

(19)

$$\begin{aligned} \alpha =\Vert (\mathcal{I}-\widehat{\mathcal{F}}'(\tilde{x}_0))^{-1}(\widehat{\mathcal{F}}(\tilde{x}_0)-\widetilde{{\mathcal{{F}}}}(\tilde{x}_0))\Vert \le \delta (1-q). \end{aligned}$$

(20)

Then, the equation $x=\widehat{\mathcal{F}}x$ has a unique solution $\hat{x}_0$ in the sphere $\Vert x-\tilde{x}_0\Vert \le \delta$. Moreover, the inequality

$$\begin{aligned} \frac{\alpha }{1+q}\le \Vert \hat{x}_0-\tilde{x}_0\Vert \le \frac{\alpha }{1-q}, \end{aligned}$$

is valid.

Theorem 6

The operators $\mathcal{T}$ and $\widetilde{{\mathcal{{T}}}}_n$ are Frechet differentiable on $\mathbb {X}$, and $\widetilde{{\mathcal{{T}}}}_{n}^{\prime }(z_0)$ is $\nu$-convergent to $\mathcal{T}'(z_0)$ in $L^2$-norm.

Proof

With the assumptions on the kernel and the nonlinear function $\psi$ and by using the Lemma 4 of [11], we get that the operator $\mathcal{T}(z)=\varPsi (\mathcal{K}z+f)$ is continuously Frechet differentiable on $\mathbb {X}$. Since $\mathcal{Q}_n$ is a linear operator, using [11, 12], it can be proved that $\widetilde{{\mathcal{{T}}}}_n(z)=\mathcal{Q}_n\varPsi (\mathcal{K}_nz+f)$ is also Frechet differentiable on $\mathbb {X}$. Denote the Frechet derivatives of $\mathcal{T}(z)$ and $\widetilde{{\mathcal{{T}}}}_n(z)$ at the point $z_0$ as $\mathcal{T}'(z_0)$ and $\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)$, respectively. Then, $\mathcal{T}'(z_0)=\varPsi '(\mathcal{K}z_0+f)\mathcal{K}$, and $\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)=\mathcal{Q}_n\varPsi '(\mathcal{K}_nz_0+f)\mathcal{K}_n$.

Now, we need to show that $\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)$ is $\nu$-convergent to $\mathcal{T}'(z_0)$ in $L^2$-norm. By using Lemma 1 and the estimate (18) with the assumptions, we obtain

$$\begin{aligned} \Vert \widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)u\Vert _{L^2}= & {} \Vert \mathcal{Q}_n\varPsi '(\mathcal{K}_nz_0+f)\mathcal{K}_nu\Vert _{L^2}\\\le & {} p\Vert \varPsi '(\mathcal{K}_nz_0+f)\Vert _{\infty }\Vert \mathcal{K}_nu\Vert _{\infty }\\\le & {} p\Big (\Vert \varPsi '(\mathcal{K}_nz_0+f)-\varPsi '(\mathcal{K}z_0+f)\Vert _{\infty }+\Vert \varPsi '(\mathcal{K}z_0+f)\Vert _{\infty }\Big )\Vert u\Vert _{L^2}\\\le & {} c(\Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{\infty }+B)\Vert u\Vert _{L^2}\le c (n^{-r}\Vert z_0\Vert _{L^2, r}+B)\Vert u\Vert _{L^2}. \end{aligned}$$

This shows that $\Vert \widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)\Vert _{L^2}$ is uniformly bounded. Next, we consider

$$\begin{aligned} \Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )u\Vert _{L^2}= & {} \Vert \Big (\mathcal{Q}_n\varPsi '(\mathcal{K}_n z_0+f)\mathcal{K}_n-\varPsi '(\mathcal{K}z_0+f)\mathcal{K}\Big )u\Vert _{L^2}\\\le & {} \Vert \Big (\mathcal{Q}_n\varPsi '(\mathcal{K}_n z_0+f)-\mathcal{Q}_n\varPsi '(\mathcal{K}z_0+f)\Big )\mathcal{K}_n u\Vert _{L^2}\\+ & {} \Vert \Big (\mathcal{Q}_n\varPsi '(\mathcal{K}z_0+f)\mathcal{K}_n-\mathcal{Q}_n\varPsi '(\mathcal{K}z_0+f)\mathcal{K}\Big )u\Vert _{L^2}\\+ & {} \Vert \Big (\mathcal{Q}_n\varPsi '(\mathcal{K}z_0+f)\mathcal{K}-\varPsi '(\mathcal{K}z_0+f)\mathcal{K}\Big )u\Vert _{L^2}\\\le & {} 2pc_2\Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{\infty }\Vert \mathcal{K}_nu\Vert _{\infty }+\sqrt{2}pB\Vert (\mathcal{K}_n-\mathcal{K})u\Vert _{\infty }\\+ & {} \Vert (\mathcal{Q}_n-\mathcal{I})\varPsi '(\mathcal{K}z_0+f)\mathcal{K}u\Vert _{L^2}. \end{aligned}$$

By using Theorem 2, the first two terms of the right hand side of the above equation $\rightarrow 0$ as $n\rightarrow \infty$. Since $\varPsi '(\mathcal{K}z_0+f)$ is bounded and $\mathcal{K}$ is a compact operator, $\varPsi '(\mathcal{K}z_0+f)\mathcal{K}$ is also a compact operator. Since $\mathcal{Q}_n$ converges pointwise to the identity operator $\mathcal{I}$ from Lemma 1 and $\varPsi '(\mathcal{K}z_0+f)\mathcal{K}$ is a compact operator, it follows that $\Vert (\mathcal{Q}_n-\mathcal{I})\varPsi '(\mathcal{K}z_0+f)\mathcal{K}u\Vert _{L^2}\rightarrow 0$ as $n\rightarrow \infty$. Thus,

$$\Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )u\Vert _{L^2}\rightarrow 0,\, \text{ as }\, n\rightarrow \infty .$$

Let B be a closed unit ball in $\mathcal{C}[-1,1]$. Since $\mathcal{T}'(z_0)=\varPsi '(\mathcal{K}z_0+f){\mathcal{K}}$ is a compact operator, $S=\{\mathcal{T}'(z_0)x: x\in B\}$ is a relatively compact set in $\mathcal{C}[-1,1]$. Then, it follows that

$$\begin{aligned} \Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )\mathcal{T}'(z_0)\Vert _{L^2}= & {} \sup \{\Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )\mathcal{T}'(z_0)u\Vert _{L^2}:\;u\in B\}\\= & {} \sup \{\Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )u\Vert _{L^2}:\;u\in S\}\rightarrow 0,\;\text{ as }\;n\rightarrow \infty . \end{aligned}$$

Since $\mathcal{Q}_n$ is uniformly bounded in $L^2$ norm, $\varPsi '(\mathcal{K}_nz_0+f)$ is also bounded and $\mathcal{K}_n$ is a compact operator, and then $\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)=\mathcal{Q}_n\varPsi '(\mathcal{K}_nz_0+f)\mathcal{K}_n$ is a compact operator. Proceeding in the similar way as in before, it can be easy to show that

$$\begin{aligned} \Vert \Big (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\mathcal{T}'(z_0)\Big )\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)u\Vert _{L^2}\rightarrow 0 \,\text{ as }\,\, n\rightarrow \infty . \end{aligned}$$

This shows that $\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)$ is $\nu$-convergent to $\mathcal{T}'(z_0)$ in $L^2$-norm. This completes the proof.

Theorem 7

Let $z_0\in \mathcal{C}^{r}[-1, 1]$ be an isolated solution of the Eq. (6). Assume that one is not an eigenvalue of the linear operator $\mathcal{T}'(z_0)$. Then for sufficiently large n, the operators $(\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))$ are invertible on $\mathbb {X}$ and there exist constants $A_1>0$ independent of n such that $\Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))^{-1}\Vert _{L^2}\le A_1$.

Proof

The proof completes by combining the Theorems 3 and 6.

Theorem 8

Let $\mathcal{Q}_n: \mathbb {X}\rightarrow \mathbb {X}_n$ be the interpolatory projection operator defined by (9). Then Eq. (17) has an unique solution $\tilde{z}_n\in B(z_0, \delta )=\{z: \Vert z-z_0\Vert _{L^2}< \delta \}$ for some $\delta >0$ and for sufficiently large n. Moreover, there exists a constant $0<q<1$, independent of n such that

$$\begin{aligned} \frac{\beta _n}{1+q}\le \Vert \tilde{z}_n-z_0\Vert _{L^2}\le \frac{\beta _n}{1-q}, \end{aligned}$$

where $\beta _n=\Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))^{-1}(\widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0))\Vert _{L^2}$.

Proof

From Theorem 7, we have $(\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))^{-1}$ that exists and it is uniformly bounded in $L^2$ norm; i.e., there exists $A_1>0$ such that $\Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))^{-1}\Vert _{L^2}\le A_1$.

Using Theorem 4 with the assumption (v), for any $z\in B(z_0, \delta )$ and $u\in \mathcal{C}[-1, 1]$, we get

$$\begin{aligned} \Vert (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z)-\widetilde{\mathcal{T}}'_n(z_0))u\Vert _{L^2}= & {} \Vert [\mathcal{Q}_n\varPsi '(\mathcal{K}_nz_0+f)\mathcal{K}_n-\mathcal{Q}_n\varPsi '(\mathcal{K}_nz+f)\mathcal{K}_n]u\Vert _{L^2}\\= & {} \Vert \mathcal{Q}_n(\varPsi '(\mathcal{K}_nz_0+f)\mathcal{K}_n-\varPsi '(\mathcal{K}_nz+f)\mathcal{K}_n)u\Vert _{L^2}\\\le & {} p\Vert (\varPsi '(\mathcal{K}_nz_0+f)-\varPsi '(\mathcal{K}_nz+f))\mathcal{K}_nu\Vert _{\infty }\\\le & {} c\Vert \mathcal{K}_n(z_0-z)\Vert _{\infty }\Vert \mathcal{K}_nu\Vert _{\infty }\le c\Vert z-z_0\Vert _{L^2}\Vert u\Vert _{L^2}. \end{aligned}$$

Thus, $\Vert (\widetilde{{\mathcal{{T}}}}^{\prime }_n(z)-\widetilde{\mathcal{T}}'_n(z_0))\Vert _{L^2}\le c\delta$. Hence, we obtain

$$\begin{aligned} \sup _{\Vert z-z_0\Vert _{L^2}\le \delta }\Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0))^{-1}(\widetilde{{\mathcal{{T}}}}^{\prime }_n(z_0)-\widetilde{{\mathcal{{T}}}}^{\prime }_n(z))\Vert _{L^2}\le A_1c\delta \le q, \end{aligned}$$

where $0<q<1$. This proves Eq. (19) of Theorem 5. Now by using Theorem 2 with Lemma 1, we obtain

$$\begin{aligned} \Vert \widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0)\Vert _{L^2}= & {} \Vert \mathcal{Q}_n\varPsi (\mathcal{K}_nz_0+f)-\varPsi (\mathcal{K}z_0+f)\Vert _{L^2}\nonumber \\\le & {} \Vert \mathcal{Q}_n[\varPsi (\mathcal{K}_nz_0+f)-\varPsi (\mathcal{K}z_0+f)]\Vert _{L^2}\nonumber \\+ & {} \Vert (\mathcal{Q}_n-\mathcal{I})\varPsi (\mathcal{K}z_0+f)\Vert _{L^2}\nonumber \\\le & {} c\Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{\infty }+\Vert (\mathcal{Q}_n-\mathcal{I})z_0\Vert _{L^2}\nonumber \\\le & {} c n^{-r}\Vert z_0\Vert _{L^2, r}+n^{-r}\Vert z_0\Vert _{L^2, r}\rightarrow 0,\,\,\text{ as }\,\,n\rightarrow \infty . \end{aligned}$$

(21)

Hence,

$$\begin{aligned} \beta _n= & {} \Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}_n(z_0))^{-1}(\widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0))\Vert _{L^2}\le A_1 \Vert \widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0)\Vert _{L^2}\rightarrow 0, \end{aligned}$$

as $n\rightarrow \infty$. Choose n large enough such that $\beta _n\le \delta (1-q)$. Then, Eq. (20) of Theorem 5 is satisfied. Thus, by applying Theorem 5, we obtain

$$\begin{aligned} \frac{\beta _n}{1+q}\le \Vert z_0-\tilde{z}_n\Vert _{L^2}\le \frac{\beta _n}{1-q}, \end{aligned}$$

(22)

where $\beta _n=\Vert (\mathcal{I}-\widetilde{{\mathcal{{T}}}}_n(z_0))^{-1}(\widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0))\Vert _{L^2}$. Using Eq. (21) with Eq. (22), we obtain

$$\begin{aligned} \Vert z_0-\tilde{z}_n\Vert _{L^2}\le & {} \beta _n\le A_1\Vert \widetilde{{\mathcal{{T}}}}_n(z_0)-\mathcal{T}(z_0)\Vert _{L^2}\le c n^{-r}\Vert z_0\Vert _{L^2, r}+n^{-r}\Vert z_0\Vert _{L^2, r}. \end{aligned}$$

(23)

This completes the proof.

Theorem 9

Let $z_0$ be the isolated solution of Eq. (6) and $u_0$ be the isolated solution of (3) such that $u_0=\mathcal{K}z_0+f$. Let $\tilde{u}_n=\mathcal{K}_n\tilde{z}_n+f$ be the discrete Legendre collocation approximation of $u_0$. Then, the following hold.

$$\begin{aligned} \Vert u_0-\tilde{u}_n\Vert _{L^2}=\mathcal{O}(n^{-r}),\,\,\,\, \Vert u_0-\tilde{u}_n\Vert _{\infty }=\mathcal{O}(n^{-r}). \end{aligned}$$

Proof

Using Theorems 4 and 2, we obtain

$$\begin{aligned} \Vert u_0-\tilde{u}_n\Vert _{L^2}= & {} \Vert \mathcal{K}z_0+f-(\mathcal{K}_n\tilde{z}_n+f)\Vert _{L^2}\\\le & {} \Vert \mathcal{K}_n(z_0-\tilde{z}_n)\Vert _{L^2}+ \Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{L^2}\\\le & {} \sqrt{2}\Vert \mathcal{K}_n(z_0-\tilde{z}_n)\Vert _{\infty }+ \sqrt{2}\Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{\infty }\\\le & {} \sqrt{2}c\Vert z_0-\tilde{z}_n\Vert _{L^2}+\sqrt{2}n^{-r}\Vert z_0\Vert _{L^2, r}. \end{aligned}$$

Using the estimate (23), we obtain

$$\begin{aligned} \Vert u_0-\tilde{u}_n\Vert _{L^2}=\mathcal{O}(n^{-r}). \end{aligned}$$

Now for the second estimate, using Theorem 2 with the estimate (23), we obtain

$$\begin{aligned} \Vert u_0-\tilde{u}_n\Vert _{\infty }\le & {} \Vert \mathcal{K}_n(z_0-\tilde{z}_n)\Vert _{\infty }+ \Vert (\mathcal{K}_n-\mathcal{K})z_0\Vert _{\infty }\\ {}\le & {} c\Vert z_0-\tilde{z}_n\Vert _{L^2}+ c n^{-r}\Vert z_0\Vert _{L^2, r}\le c n^{-r}. \end{aligned}$$

This completes the proof.

Remark 1

From Theorem 9, we observe that the Legendre collocation solution converges to the exact solution with the order $\mathcal{O}(n^{-r})$ in both $L^2$ and infinity norm. We obtained the similar convergence rates for Legendre collocation methods for Fredholm–Hammerstein integral equations with weakly singular kernel using piecewise polynomial-based collocation methods.

4 Numerical Examples

In this section, we present an example to validate the errors of the approximation solutions by using Legendre collocation methods both in $L^2$ and infinity norm. To solve the problem by using Legendre collocation methods, we first choose Legendre polynomials as the basis functions of $\mathbb {X}_n$ evaluated from the recurrence relation,

$$\begin{aligned} \phi _0(x) = 1,\;\; \phi _1(x) = x,\; x \in [-1,1], \end{aligned}$$

and for $i=1,2,\cdots , n-1,$

$$\begin{aligned} (i+1)\phi _{i+1}(x) = (2i+1)x\phi _{i}(x) - i \phi _{i-1}(x),\; x \in [-1,1]. \end{aligned}$$

Example 1

We consider the following integral equation

$$\begin{aligned} x(t)-\frac{1}{\sqrt{2}}\int _{-1}^1 \frac{1}{\sqrt{|s-t|}}\cos {\Big (\frac{s+1}{2}+x(s)\Big )}ds=f(t),\,\,t\in [-1,1], \end{aligned}$$

where f(t) is selected so that $\displaystyle x(t)=\cos {\Big (\frac{t+1}{2}\Big )}$ is the solution.

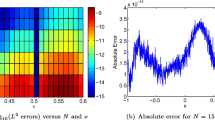
For different values of n, we compute $\tilde{u}_n$ and compare the results with exact solution $u_0$. The computed errors in $L^2$ and infinity norm are presented in Table 1.

Table 1 Discrete Legendre collocation method