On Love Wave Frequency Under the Influence of Linearly Varying Shear Moduli, Initial Stress, and Density of Orthotropic Half-Space

Abstract

The present work studies Love wave propagation in an inhomogeneous anisotropic layer superimposed over an inhomogeneous orthotropic half-space under the influence of rigid boundary plane. The layer exhibits inhomogeneity which varies quadratically with depth, whereas the half-space has inhomogeneity in the shear moduli, density, and initial stress which varies linearly downward. The frequency equation is deduced in the closed form. It has been found that the dispersion equation is a function of phase velocity, wave number, inhomogeneity parameters, and initial stress. To analyze the result more profoundly, numerical simulation and graphical illustrations have been effectuated to depict the pronounced impact of the affecting parameters on the phase velocity of Love wave. As a special case, the procured dispersion relations have been found in well agreement with the standard Love wave equation.

1 Introduction

It is very interesting to study Love wave propagation in an anisotropic media because the dispersion of seismic waves in anisotropic and orthotropic media is elementarily different from their dispersion in isotropic media. As the crustal layer of earth and mantle are not found to be homogeneous, it is very interesting to know the dispersion pattern of Love wave in an inhomogeneous medium as is studied sufficiently by Shearer [13]. It has been noticed that the propagation of Love wave is mostly affected by the elastic properties and the characteristic of the medium which it travels through. The earths’ mantle (half-space) contains some hard and soft rocks or materials that may exhibit orthotropic property and porosity. In orthotropic medium, the thermal or mechanical properties being unique and independent in three mutually perpendicular directions make it an interesting medium. These facts motivated us to investigate further on Love wave propagation where the bearing of linear variation in the rigidity, density, and initial stresses can be studied. Destrade [5] studied in detail surface waves in orthotropic being incompressible in nature, whereas Kumar and Rajeev [11] analyzed the seismic wave motion to show the effect of voids at the boundary surface of orthotropic thermoelastic material. Ahmed and Dahab [1] demonstrated the remarkable effect of orthotropic granular layer on Love wave propagation, while a clear picture has been explained by Kumar and Choudhury [10] about the behavior and the response of orthotropic micropolar elastic medium via various sources.

Many problems in field of theoretical seismology are likely to be solved by demonstrating the earth as a layered medium with certain finite thickness and mechanical properties. An accurate and precise study on dispersion of elastic wave and its generation had been made by Chapman [4]. Propagation of surface seismic waves in the earths’ crust due to its multiple applications in the field of geophysics, seismology, and applied mathematics has always been the subject of discussion along with various investigations. Vishwakarma et al. [14] demonstrated about the influence of the rigid boundary playing on the Love wave propagation in the elastic layer with void pores, while an interesting study made by Ke et al. [9] on Love wave dispersion under the effect of linearly varying properties of an inhomogeneous fluid saturated porous-layered half-space. In the theoretical study of seismic waves, mathematical expression provides the bridge between modeling results and field application. The propagation of elastic/seismic waves through the interior part of earth is governed by mathematical laws similar to the laws of light waves in optics.

The propagation of surface seismic wave such as Love waves in various inhomogeneous media has importance in multiple branches of engineering and applied science, like geophysics, seismology, earth science. Several studies have been carried out to understand the propagation technique of seismic waves in the inhomogeneous medium. Theories related to Love wave propagation in the anisotropic and inhomogeneous media have significant practical importance. It not only helps to investigate the internal structure of the earth and exploration of natural resources buried in the earths’ surface but also about the composition of several layers under immense stress owing to different physical causes, i.e., presence of overlying layers, variation in temperature and gravitational field. This wave disperses when the solid medium near the surface has inhomogeneous elastic properties. Fortunately, Biot [2] developed the incremental deformation theory for pre-stressed medium. Adapting the same theory, earth being a spherical body with finite dimension, there exist remarkable influence of earths’ crust on seismic surface waves. This phenomenon motivated us to investigate boundary waves or surface waves, i.e., waves that remain confined to certain surfaces during their dispersion. The formulations, solutions, and numerical simulations of many problems related to linear wave propagation for variety of geomedia may be found in the work of Gupta et al. [7, 8].

However, no attempt has been made to show the influence of inhomogeneous orthotropic half-space under initial stress on Love wave propagation. Therefore, in the present study, the half-space has been taken as inhomogeneous orthotropic medium followed by an inhomogeneous anisotropic layer resting over it. The inhomogeneity taken in the orthotropic mantle varies linearly along depth down toward the central core of the earth. This linear inhomogeneity has been taken in shear moduli, density, and initial stress of the half-space whereas the layer exhibits a quadratic variation in directional rigidities along horizontal and vertical direction and density. Suitable boundary condition under the assumption of rigid boundary plane has been considered and imposed on the displacement of the wave which have been found for individual layers. The frequency equation (dispersion equation) has been derived in closed form along with various particular cases. When all the inhomogeneities vanish, the frequency equation reduces to a classical equation of Love wave given by Love [12]. Numerical magnitude of the phase velocity has been calculated with the help of values of the material constants given by Biot [2] from experiments, and the effect of inhomogeneity parameter associated with directional rigidities, density, and initial stress is discussed and demonstrated using graphs.

2 Statement of the Problem

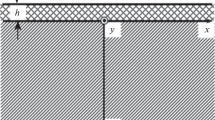
The geometry of the problem consists of an inhomogeneous anisotropic earth crust of finite thickness H resting over an inhomogeneous orthotropic half-space under the influence of linearly varying initial stress. Cartesian coordinate system has been employed with z-axis directed downwards and origin being at the interface where crustal layer and half-space meet as shown in the 3D diagram of Fig. 1. The upper boundary plane of the layer has been kept rigid where displacement of the wave vanishes. The inhomogeneities considered in the layer are as follows:

$$\begin{aligned} N =\overline{N}\left( 1+az\right) ^2, L =\overline{L}\left( 1+az\right) ^2, \rho =\overline{\rho }\left( 1+az\right) ^2 \end{aligned}$$

(1)

where $\overline{N}$ and $\overline{L}$ are the values of directional rigidities along x and z directions and $\overline{\rho }$ is the density at $z=0$, a is called inhomogeneity parameter with dimension same as that of inverse of length.

The inhomogeneities taken in the anisotropic half-space are

$$\begin{aligned} Q_1 =\overline{Q_1}\left( 1+\alpha z\right) , Q_3 =\overline{Q_3}\left( 1+\beta z\right) , P =\overline{P}\left( 1+\gamma z\right) , \rho _1 =\overline{\rho _1}\left( 1+\delta z\right) \end{aligned}$$

(2)

where $\overline{Q_1}$, $\overline{Q_3}$, $\overline{P}$, and $\overline{\rho _1}$ are shear moduli, initial stress, and density of the medium at the interface $z=0$ and $\alpha$, $\beta$, $\gamma$, and $\delta$ are the inhomogeneity parameter associated with it having dimension equal to that of inverse length. Variation of rigidity, density, and initial stress along the depth inside the earth effects the propagation of seismic waves to a great extent. The inhomogeneity that exists is caused by variation in rigidity and density. The crust region of our planet is composed of various inhomogeneous layers with different geological parameters. As pointed out by Bullen [3], the density inside the earth varies at different rates with different layers within the earth. He approximated density law inside the earth as a quadratic polynomial in depth parameter for 413–984 km depth. For depth from 984 km to central core, Bullen approximated the density as a linear function of depth parameter, and hence based on these theories, we have taken quadratic and linear variations.

Fig. 1

Three-dimensional geometry of the problem

3 Solution

3.1 Finding Displacement in Anisotropic Inhomogeneous Layer

Let $u_1$, $v_1$ and $w_1$ be the displacement components in the x, y, and z direction, respectively. Starting from the general equation of motion and using the conventional Love waves conditions, viz. $u=0$, $w=0$ and $v=v_1(x, z, t)$, the only y component. Then, the equation of motion in the absence of body force can be written as Biot [2]

$$\begin{aligned} N \frac{\partial ^2 v_1}{\partial x^2}+\frac{\partial }{\partial z}\left( L\frac{\partial v_1}{\partial z}\right) =\rho \frac{\partial ^2 v_1}{\partial t^2} \end{aligned}$$

(3)

For a wave propagation along x-direction, we may assume

$$\begin{aligned} v_1=V(z)e^{ik(x-ct)} \end{aligned}$$

(4)

Using Eqs. (3) and (4) takes the form

$$\begin{aligned} \frac{d^2V}{dz^2}+\frac{1}{L}\frac{dL}{dZ}\frac{dV}{dz}+\frac{K^2}{L}\left( c^2\rho -N \right) V=0 \end{aligned}$$

(5)

After putting $V=\frac{V_1}{L}$ in equation, we get

$$\begin{aligned} \frac{d^2 V_1}{dz^2}-\frac{1}{2L}\frac{d^2L}{dz^2}V_1+\frac{1}{4L^2}\left( \frac{dL}{dz}\right) ^2V_1+\frac{K^2}{L}\left( c^2\rho -N\right) V_1=0 \end{aligned}$$

(6)

Using the inhomogeneity taken in Eqs. (1) and (6) changes to

$$\begin{aligned} \frac{d^2V_1}{dz^2}+m_1^2V_1=0 \end{aligned}$$

(7)

$$\begin{aligned} \text{ where }, \, \,m_1^2=\frac{K^2}{\overline{L}}\left( c^2\overline{\rho }-\overline{N}\right) \end{aligned}$$

(8)

The solution of Eq. (7) may be assumed as

$$V_1=A_1e^{im_1z}+B_1e^{-im_1z}$$

Thus, Eq. (4), the displacement in the inhomogeneous anisotropic layer may be taken as

$$\begin{aligned} v_1=\frac{A_1e^{im_1z}+B_1e^{-im_1z}}{\sqrt{\overline{L}}\left( 1+az\right) }e^{iK(x-ct)} \end{aligned}$$

(9)

3.2 Finding Displacement for Inhomogeneous Orthotropic Half-Space

The half-space taken in the problem is inhomogeneous orthotropic in nature under the influence of initial stress P along x direction as shown in Fig. 1. The system of equation pertaining to wave motion when there is no body forces is given by Biot [2]

(10)

where $u_2$, $v_2$, and $w_2$ are the displacement components while $w_x$, $w_y$, and $w_z$ are the rotational components along x, y, and z direction. Here, $\sigma _{ij}$ are the incremental stress components and $\rho _1$ is the density of orthotropic medium. The relations between the strain and the incremental stress components are

(11)

where $B_{ij}$ and $Q_i$ are the incremental normal elastic coefficients and shear moduli, respectively. Here $e_{ij}$ are the strain components, which is defined by

$e_{ij}=\frac{1}{2}\left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$, where $i,j=1,2,3.$

Now, as per the characteristic of Love wave propagation, $u_2=0, w_2=0$, and $v_2=v_2(x, z, t)$. Also, the inhomogeneity taken in Eq. (2) in Eq. (10) reduces to

$$\begin{aligned} \overline{Q}_3\left( 1+\beta z\right) \frac{\partial ^2 v_2}{\partial x^2}+\overline{Q}_1\alpha \frac{\partial ^2v_2}{\partial z^2}+\overline{Q}_1\left( 1+\alpha z\right) \frac{\partial ^2v_2}{\partial z^2}-\frac{\overline{P}}{2}\left( 1+\gamma z\right) \frac{\partial ^2 v_2}{\partial x^2}=\overline{\rho _1}\left( 1+\delta z\right) \frac{\partial ^2 v_2}{\partial t^2} \end{aligned}$$

(12)

We may now use separation of variable, i.e., $v_2=V_2\left( z\right) e^{ik(x-ct)}$, where k is the wave number and c is the phase velocity. Eq. (12) may now be written as

$$\begin{aligned} \frac{d^2 V_2}{dz^2}+\frac{\alpha }{\left( 1+\alpha z\right) }\frac{dV_2}{dz}+k^2 \left\{ A_1\frac{\left( 1+\gamma z\right) }{\left( 1+\alpha z\right) }+ A_2\frac{\left( 1+\delta z\right) }{\left( 1+\alpha z\right) }- A_3\frac{\left( 1+\beta z\right) }{\left( 1+\alpha z\right) }\right\} V_2=0 \end{aligned}$$

(13)

$$\begin{aligned} \text{ where }, \, \,A_1=\frac{\overline{P}}{2\overline{Q}_1},\, A_2=\frac{c^2}{c_1^2},\, A_3=\frac{\overline{Q}_3}{\overline{Q}_1}, \,c_1^2=\frac{\overline{Q}_1}{\overline{\rho }_1} \end{aligned}$$

(14)

Now, substituting $V_2=\frac{\psi (z)}{\left( 1+\alpha z\right) ^{1/2}}$ in Eq. (13) to eliminate $\frac{dV_2}{dz}$, we get

$$\begin{aligned} \frac{d^2\psi }{dz^2}+k^2\left\{ A_1\frac{\left( 1+\gamma z\right) }{\left( 1+\alpha z\right) }+ A_2\frac{\left( 1+\delta z\right) }{\left( 1+\alpha z\right) }- A_3\frac{\left( 1+\beta z\right) }{\left( 1+\alpha z\right) }+\frac{1}{4}\left( \frac{a}{k}\right) ^2\frac{1}{\left( 1+\alpha z\right) ^2}\right\} \psi =0 \end{aligned}$$

(15)

Putting $n=2\left( 1+\alpha z\right) \left( \frac{k}{\alpha }\right) \sqrt{A_3\left( \frac{\beta }{\alpha }\right) -A_1\left( \frac{\gamma }{\alpha }\right) -A_2\left( \frac{\delta }{\alpha }\right) }$, we will get

$$\begin{aligned} \frac{d^2\psi }{d\eta ^2}+\left( \frac{1}{4\eta ^2}+\frac{R}{\eta }-\frac{1}{4}\right) \psi =0 \end{aligned}$$

(16)

$\text{ where }, \, \,R=\frac{1}{2}\left( \frac{k}{\alpha }\right) \left\{ A_3\left( \frac{\beta }{\alpha }\right) -A_1\left( \frac{\gamma }{\alpha }\right) +A_2\left( \frac{\delta }{\alpha }\right) \right\} ^{\frac{1}{2}}\bigg \{A_1\left( \frac{\gamma }{\alpha }-1\right) +A_2\left( \frac{\delta }{\alpha }-1\right) +A_3\left( 1-\frac{\beta }{\alpha }\right) \bigg \}$

Equation (16) is a well-known Whittakers’ equation, and the solution of which can be written as

$$\psi =A_2W_{R,0}\left( \eta \right) +B_2 W_{-R,0}\left( -\eta \right) $$

where $W_{R,0}\left( \eta \right)$ is Whittakers’ function and the general expansion of $W_{R,m}\left( \eta \right)$ may be written as Whittaker and Watson [15]

$$\begin{aligned} \begin{aligned} W_{R,m}\left( \eta \right) =e^{-\frac{\eta }{2}}.R^\eta \left[ 1+\frac{\left\{ m^2-\left( R-\frac{1}{2}\right) ^2\right\} }{1! z}+\frac{\left\{ m^2-\left( R-\frac{1}{2}\right) ^2\right\} \left\{ m^2-\left( R-\frac{3}{2}\right) ^2\right\} }{2! z^2}+\dots \right] \end{aligned} \end{aligned}$$

(17)

Thus, the displacement in inhomogeneous orthotropic half-space becomes

$$\begin{aligned} v_2=\frac{\left\{ A_2 W_{R,0}\left( \eta \right) +B_2 W_{-R,0}\left( -\eta \right) \right\} }{\left( 1+\alpha z\right) ^\frac{1}{2}}e^{ik(x-ct)} \end{aligned}$$

(18)

But, as we go down deep toward the center of earth, the displacement vanishes, i.e, as $z \rightarrow \infty$, $\nu _2 \rightarrow 0$, and therefore, the displacement in Eq. (18) reduces to

$$\begin{aligned} v_2=\frac{A_2W_{R,0}\left( \eta \right) }{\left( 1+\alpha z\right) ^{\frac{1}{2}}}e^{ik(x-ct)} \end{aligned}$$

(19)

4 Boundary Conditions and Dispersion Equation

• (1) Due to the presence of rigid boundary plane at $Z=-H$, the displacement vanishes

  $$\begin{aligned} v_1=0 \,\, at \,\, z=-H \end{aligned}$$

  (20a)

• (2) Displacement being continuous at the interface implies that

  $$\begin{aligned} v_1=v_2 \, \, at \, \, z=0 \end{aligned}$$

  (20b)

• (3) At the contact plane $z=0$, the continuity of the stress requires that

  $$\begin{aligned} L\frac{\partial v_1}{\partial z}=Q_1\frac{\partial v_2}{\partial z} \, \, \, at \, \, \, z=0 \end{aligned}$$

  (20c)

Using the above boundary conditions one by one, and eliminating the arbitrary constants $A_1$, $B_1$, and $A_2$ for nontrivial solution, we will have the following determinant.

$$\begin{aligned} \begin{vmatrix} e^{-im_1H}&e^{im_1H}&0\\&&\\ \frac{1}{\sqrt{\overline{L}}}&\frac{1}{\sqrt{\overline{L}}}&-W_{R,0}\left( \overline{\eta }\right) \\&&\\ \sqrt{\overline{L}}\left( im_1-a\right)&-\sqrt{\overline{L}}\left( im_1+a\right)&-\overline{Q}_1\left[ \frac{\partial W_{R,0}\left( \eta \right) }{\partial \eta }.\frac{d\eta }{dz}\right] _{z=0} \end{vmatrix} =0 \end{aligned}$$

(21)

Expanding the above determinant, we get the following:

$$\begin{aligned} \begin{aligned} cot(m_1H) =&\left( \frac{a}{m_1}\right) \left( 1+2\left( \frac{\overline{Q_1}}{\overline{L}}\right) \left( \frac{k}{a}\right) \left\{ A_3\left( \frac{\beta }{\alpha }\right) -A_1\left( \frac{\gamma }{\alpha }\right) -A_2\left( \frac{\delta }{\alpha }\right) \right\} ^{1/2}\right) \\&\left[ -\frac{1}{2}+\frac{R}{\overline{\eta }}+\frac{\left( R-0.5\right) ^2}{\overline{\eta }^2}\left\{ 1-\frac{\left( R-0.5\right) ^2}{\overline{\eta }}\right\} ^{-1}\right] \end{aligned} \end{aligned}$$

Substituting the value of $m_1$ in the above expansion, it reduces to

$$\begin{aligned} \begin{aligned} cot\left( kH\sqrt{\frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}}\right) = \left( 1+2\left( \frac{\overline{Q_1}}{\overline{L}}\right) \left( \frac{k}{a}\right) \left\{ A_3\left( \frac{\beta }{\alpha }\right) -A_1\left( \frac{\gamma }{\alpha }\right) -A_2\left( \frac{\delta }{\alpha }\right) \right\} ^{1/2}\right) \\ \left[ -\frac{1}{2}+\frac{R}{\overline{\eta }}+\frac{\left( R-0.5\right) ^2}{\overline{\eta }^2}\left\{ 1-\frac{\left( R-0.5\right) ^2}{\overline{\eta }}\right\} ^{-1}\right] \left( \frac{a}{k}\left( \frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}\right) ^{-1/2}\right) \end{aligned} \end{aligned}$$

(22)

where $c_0^2=\frac{\overline{L}}{\overline{\rho }}.$

Equation (22) is the required frequency equation of Love wave propagation in an inhomogeneous anisotropic layer resting over an inhomogeneous orthotropic medium with rigid boundary plane at the top. We find that Eq. (22) is a function of dimensionless phase velocity $\left( \frac{c^2}{c_0^2}\right)$, dimensionless wave number kH along with the inhomogeneity parameters m, $\alpha$, $\gamma$, and $\delta$ associated with the rigidities, densities, and initial stress of the medium taken in to consideration.

Particular Case:

Case-I: When there is no inhomogeneity in the layer $a \rightarrow 0$, then Eq. (22) reduces to

$$\begin{aligned} \begin{aligned} cot\left( kH\sqrt{\frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}}\right)&=2\left( \frac{\overline{Q_1}}{\overline{L}}\right) \left\{ A_3\left( \frac{\beta }{\alpha }\right) -A_1\left( \frac{\gamma }{\alpha }\right) -A_2\left( \frac{\delta }{\alpha }\right) \right\} ^{1/2}\\&\left[ -\frac{1}{2}+\frac{R}{\overline{\eta }}+\frac{\left( R-0.5\right) ^2}{\overline{\eta }^2}\left\{ 1-\frac{\left( R-0.5\right) ^2}{\overline{\eta }}\right\} ^{-1}\right] \left( \frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}\right) ^{-1/2} \end{aligned} \end{aligned}$$

which is the frequency equation of Love wave in a homogeneous anisotropic layer over inhomogeneous orthotropic half-space.

Case-II: When the half-space is stress-free, i.e., $\overline{P} \rightarrow 0$, then Eq. (22) becomes

$$\begin{aligned} \begin{aligned} cot\left( kH\sqrt{\frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}}\right)&=\left( 1+2\left( \frac{\overline{Q_1}}{\overline{L}}\right) \left( \frac{k}{a}\right) \left\{ A_3\left( \frac{\beta }{\alpha }\right) -A_2\left( \frac{\delta }{\alpha }\right) \right\} ^{1/2}\right) \\&\left[ -\frac{1}{2}+\frac{R}{\overline{\eta }}+\frac{\left( R-0.5\right) ^2}{\overline{\eta }^2}\left\{ 1-\frac{\left( R-0.5\right) ^2}{\overline{\eta }}\right\} ^{-1}\right] \left( \frac{a}{k}\left( \frac{c^2}{c_0^2}-\frac{\overline{N}}{\overline{L}}\right) ^{-1/2}\right) , \end{aligned} \end{aligned}$$

which is the frequency equation of Love wave in an inhomogeneous anisotropic layer resting over inhomogeneous orthotropic half-space with no initial stress.

Case-III: When $\overline{N}=\overline{L}$, $\overline{Q_1}=\overline{Q_2}$, $a\rightarrow 0$, $\alpha \rightarrow 0$, $\beta \rightarrow 0$, $\delta \rightarrow 0$ and $P\rightarrow 0$, then the frequency Eq. (22) becomes

$$cot\left( kH\sqrt{\frac{c^2}{c_0^2}-1}\right) =\frac{\overline{Q}_1}{\overline{L}}\frac{\sqrt{\frac{c^2}{c_1^2}-1}}{\sqrt{\frac{c^2}{c_0^2}-1}}$$

which is the standard classical dispersion equation of Love wave given by Love [12] and therefore validated the solution of the problem discussed.

5 Numerical Computations, Graphs, and Discussion

In order to illustrate the theoretical results obtained in the preceding sections, the data have been fetched from Gubbins [6] to study graphically the impact of inhomogeneity, rigid boundary, and the various elastic constants on the propagation of Love wave using frequency equation as obtained in Eq. (22). We will use the asymptotic linear expansion of Whittakers’ function as given in Eq. (17). In all the graphs, horizontal axis has been taken as dimensionless wave number kH while vertical axis has been taken as dimensionless phase velocity $\left( \frac{c}{c_0}\right) ^2$. Numerical values taken are as follows:

• 1. Inhomogeneous anisotropic layer: $\quad \overline{N}=7.34\times 10^{10}\hbox {N/m}^2$,    $\overline{L}=5.98\times 10^{10}\hbox {N/m}^{2} \hbox {N/m}^2$,    $\overline{\rho }=3195\,\hbox {kg/m}^3$

• 2. Inhomogeneous orthotropic half-space: $Q_1=5.82\times 10^{10} \hbox {N/m}^2$,    $\overline{Q}_3=3.99\times 10^{10} \hbox {N/m}^2$,    $\overline{\rho _1}=4500\,\hbox {kg/m}^3$

Figure 2 reflects the effect of inhomogeneity parameter $\left( \frac{a}{k}\right)$ associated with the directional rigidities and density in the anisotropic layer. The value of $\left( \frac{a}{k}\right)$ for curve no.1, curve no. 2, curve no. 3, and curve no. 4 has been taken as 0.1, 0.3, 0.5, and 0.7, respectively, whereas the value of $\frac{\overline{P}}{2\overline{Q}}$, $\frac{\alpha }{k}$, $\frac{\beta }{k}$, $\frac{\gamma }{k}$ and $\frac{\delta }{k}$ are 0.2, 0.1, 0.2, 0.2, and 0.1, respectively. The following observations and effects are obtained under the above considered values.

• 2a. The phase velocity decreases as the wave number increases for all the values of $\left( \frac{a}{k}\right)$.

• 2b. While at a particular wave number as the value of $\left( \frac{a}{k}\right)$ increases from 0.1 to 0.7, the phase velocity decreases.

• 2c. Toward low wave number, the curves seem accumulating which reveals that the phase velocity remains unaffected as inhomogeneity changes.

• 2d. Toward higher wave number, the phase velocity decreases gradually, whereas it decreases rapidly for low wave number.

• 2e. Seeing the pattern of the curve, we can claim that the inhomogeneity present in the layer bears a remarkable effect on the phase velocity of Love wave.

Figure 3 has been drawn to analyze the bearing of dimensionless inhomogeneity parameter $\left( \frac{\alpha }{k}\right)$ on the phase velocity of Love wave. Curve no. 1 has been plotted for $\frac{\alpha }{k}=0.2$, curve no. 2 for $\frac{\alpha }{k}=0.4$, curve no. 3 for $\frac{\alpha }{k}=0.6$ and curve no. 4 for $\frac{\alpha }{k}=0.8$. The value of $\frac{\overline{P}}{2\overline{Q}}$, $\frac{a}{k}$, $\frac{\beta }{k}$, $\frac{\gamma }{k}$ and $\frac{\delta }{k}$ are 0.2, 0.1, 0.2, 0.2, and 0.1, respectively. The following results are obtained.

• 3a. The pattern of curves obtained here is quite similar to one obtained in Fig. 2.

• 3b. As the magnitude of $\left( \frac{\alpha }{k}\right)$ increases from 0.2 to 0.8, the phase velocity decreases at a fixed wave number.

• 3c. Curves being equally apart, a periodic effect of inhomogeneity parameter $\frac{\beta }{k}$ may be found throughout the figure.

Fig. 2

Variation of dimensionless phase velocity against dimensionless wave number for different values of $\left( m/k\right)$ when $\frac{\overline{P}}{2\overline{Q}_1}=0.2$, $\frac{\alpha }{k}=0.1$, $\frac{\beta }{k}=0.2$, $\frac{\gamma }{k}=0.2$, $\frac{\delta }{k}=0.1$

Fig. 3

Variation of dimensionless phase velocity against dimensionless wave number for different values of $\left( \alpha /k\right)$ when $\frac{\overline{P}}{2\overline{Q}_1}=0.2$, $\frac{a}{k}=0.1$, $\frac{\beta }{k}=0.2$, $\frac{\gamma }{k}=0.2$, $\frac{\delta }{k}=0.1$

Fig. 4

Variation of dimensionless phase velocity against dimensionless wave number for different value of $\left( \beta /k\right)$ when $\frac{\overline{P}}{2\overline{Q}_1}=0.2$, $\frac{a}{k}=0.1$, $\frac{\alpha }{k}=0.1$, $\frac{\gamma }{k}=0.2$, $\frac{\delta }{k}=0.1$

Figure 4 describes the influence of inhomogeneity parameter $\left( \frac{\beta }{k}\right)$ for its increasing magnitude from 0.1 to 0.4 for curve no. 1–4. The following observations and effects are found.

• 4a. Unlike Figs. 2 and 3, the phase velocity increases for the increases in the inhomogeneity parameter $\left( \frac{\beta }{k}\right)$ associated with shear Modulus $Q_3$.

• 4b. The curves are becoming closer as the magnitude of $\left( \frac{\beta }{k}\right)$ increases.

• 4c. The impact of the inhomogeneity is more pronounced for its least value.

• 4d. It can also be said that phase velocity may attain a constant magnitude as the inhomogeneity increases further.

Figure 5 illustrates a clear picture of the variation of phase velocity against wave number when initial stress in the half-space increases. Curves have been plotted for $\frac{\gamma }{k}$ equals to 0.2, 0.4, 0.6, and 0.8 for curve no. 1, curve no. 2, curve no. 3, and curve no. 4, respectively. The values of other parameter such as $\frac{\overline{P}}{2\overline{Q}}$, $\frac{a}{k}$, $\frac{\alpha }{k}$, $\frac{\beta }{k}$, $\frac{\gamma }{k}$, and $\frac{\delta }{k}$ have been taken as 0.2, 0.1, 0.1, 0.2, 0.1. We can enlist the following points about Fig. 5.

• 5a. The pattern is similar to some extent as that of one obtained in Fig. 4.

• 5b. Here the phase velocity diminishes as the magnitude of the inhomogeneity parameter linked with initial stress increases.

• 5c. The phase velocity for curve no. 3 and curve no. 4 is restricted upto to $kH=3.5$ and $kH=2$, respectively, thereby showing a significant effect of inhomogeneity in the half-space.

Fig. 5

Variation of dimensionless phase velocity against dimensionless wave number for different value of $\left( \gamma /k\right)$ when $\frac{\overline{P}}{2\overline{Q}_1}=0.2$, $\frac{a}{k}=0.1$, $\frac{\alpha }{k}=0.1$, $\frac{\gamma }{k}=0.2$, $\frac{\delta }{k}=0.1$

Fig. 6

Variation of dimensionless phase velocity against dimensionless wave number for different value of $\left( \delta /k\right)$ when $\frac{\overline{P}}{2\overline{Q}_1}=0.2$, $\frac{a}{k}=0.1$, $\frac{\alpha }{k}=0.1$, $\frac{\beta }{k}=0.2$, $\frac{\gamma }{k}=0.2$

Fig. 7

Variation of dimensionless phase velocity against dimensionless wave number for different values of compressive initial stress $\left( \frac{P}{2Q_1}>0\right)$ when $\frac{a}{k}=0.1$, $\frac{\alpha }{k}=0.1$, $\frac{\beta }{k}=0.2$, $\frac{\gamma }{k}=0.0$, $\frac{\delta }{k}=0.1$

In Fig. 6, attempt has been made to show the influence of inhomogeneity parameter $\frac{\delta }{k}$ present in the density of the orthotropic half-space. We find that

• 6a. there is an decrement in the magnitude of phase velocity as the wave number diminishes for all the values of $\frac{\delta }{k}$.

• 6b. At a particular wave number, the phase velocity also decreases for the increasing magnitude of inhomogeneity parameter in the density of orthotropic medium.

• 6c. When the phase velocity is least, the curves appearing closer to each other at high wave number showing a prominent effect of inhomogeneity parameter $\frac{\delta }{k}$.

Figure 7 depicts the impact of initial stress $\frac{\overline{P}}{2\overline{Q}_1}$ when $\frac{\gamma }{k}=0$ shows the effect of compressive initial stress $\left( \frac{\overline{P}}{2\overline{Q}_1} > 0\right)$ on the phase velocity of Love wave propagating in an inhomogeneous anisotropic layer. It has been observed that as the magnitude of compressive initial stress becomes larger, the phase velocity decreases while it increases as the tensile stress increases.

6 Conclusion

Propagation of Love waves in an inhomogeneous anisotropic layer resting over an inhomogeneous orthotropic half-space with linearly varying inhomogeneity has been studied in details. Solutions in terms of displacement of the wave in the layer and half-space have been derived separately. We have used asymptotic linear expansion of Whittakers’ function and obtained the dispersion relation (frequency equation) in compact form. Numerical investigations have been made on phase velocity against wave number and the effect of each one of the linearly varying inhomogeneity parameters associated with anisotropic layer and orthotropic half-space has been studied and discussed in detail. We observed that

• I. Under the assumed condition, phase velocity $\left( \frac{c}{c_0}\right) ^2$ increases with decrease in dimensionless wave number.

• II. The phase velocity of Love wave decreases as the inhomogeneity parameter $\left( \frac{a}{k}\right)$ associated with directional rigidity and density of the layer increases.

• III. The increasing magnitude of $\frac{\beta }{k}$ increases the phase velocity whereas $\frac{\alpha }{k}$, $\frac{\gamma }{k}$ and $\frac{\delta }{k}$ decreases the phase velocity as it increases.

• IV. At a fixed wave number, the increasing value of compressive initial stress $\left( \frac{P}{2Q_1}>0\right)$ decreases the velocity while increasing tensile stress $\left( \frac{P}{2Q_1}>0\right)$ increases.

• V. In the absence of all inhomogeneity and initial stress, the dispersion equation turns into the classical form of equation of Love wave and therefore revealing the validation of current work.

The consequences of the present study gives a theoretical framework for the adopted model, which may likely to be utilized to collect, investigate, and recognize the propagation pattern Love wave propagation in anisotropic layer over orthotropic half-space, which may further help in accessing the resources buried inside the earth such oils, gases, minerals, deposits, and other useful hydrocarbons. Apart from these, the outcomes of the present study may also be used widely in the design and development of heavy civil construction projects involving steel structures, disaster-resistant buildings, bridge, and towers, etc. Precisely the study may also be useful in the inter-departmental fields like rock mechanics, soil mechanics, geotechnical engineering, and applied science.