Keywords

8.1 Introduction

Nowadays, Renewable energy systems receive a great interest in the research community thanks to economic, social and environmental benefits.

In fact, because of the earth greenhouse effects, the oil price increases, the nuclear world security and the rapid growth of the global economy, the renewable energy, which includes geothermal energy, wind energy and photovoltaic energy, etc., has been widely investigated and rapidly developed (Bull 2001).

Wind energy is considered to be the most competitive and the fastest growing renewable energy as it is a clean energy source with an exhaustible supply (Burton et al. 2011).

Several types of wind turbine exist nowadays with variation in the number of blades, the generator type and the control surface. The most prevalent turbine existing in the control literature is the 3-blade, horizontal axis wind turbine (HAWT).

For several decades, the wind turbine has been operated at a fixed speed. Despite it has a simple structure and a lower construction and maintenance cost, this type presents some problems as the poor power quality and the low efficiency. Thus, it has been replaced by a variable speed wind turbine (VSWT) to enhance efficiency, reduce audible noise and mechanical stresses (Abulanwar et al. 2016; Burton et al. 2011; Yang et al. 2014b).

For VSWT, the direct− driven permanent magnet synchronous generators (PMSG) are widely used in small and medium-size wind turbine systems. There are several advantages of using PMGs for electrical power generations.

First, they can provide high-reliability and high-efficiency, since there are no copper losses in the rotor circuit and no need for external excitation (Cai et al. 2000).

Second, PMGs with high−power−density are small in size, which reduces the weight and the cost of the wind turbine system (Michalke et al. 2007).

In addition, the wind turbine with a direct-drive PMSG offers the ability to remove the gearbox. According to the statistical data reported in Ribrant and Bertling (2007), failures of gearboxes cause about 19.4% downtime of WTGs. Without gearboxes, the system needs less maintenance and have a higher reliability and a reduced downtime.

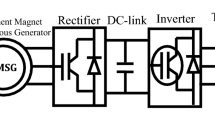
The overall configuration of a direct-drive PMSG wind turbine shown in Fig. 8.1. This structure includes a generator control for maintaining the desired rotor speed, a pitch angle control for limiting the output power, a constant DC link control and a grid side inverter control for active and reactive power control.

Fig. 8.1
figure 1

Process structure

Full size image

The main challenge in wind energy conversion system (WECS) control is to extract the optimal accessible power and cope with the nonlinearity of the system. Therefore, in this chapter, we will focus only on analyzing modern nonlinear control techniques for the generator-side to achieve maximum performances.

For the generator side, there are typically two control strategies according to the wind speed velocity.

In partial load region, the speed controller can continually adjust the speed of the rotor to ensure as much as possible energy yield. Thus, the efficiency of the system will be increased.

For full load zone, the pitch angle regulation is required to keep the generated power constant.

In wind turbine system, control strategies hold a crucial role to enhance the efficiency. Without a good control system, a considerable portion of the produced power is wasted.

Several works of the literature are addressing the issue of controlling the wind turbine system. The simplest techniques are based on PI controllers and the Perturb and Observe algorithm (Kesraoui et al. 2011; Mansour et al. 2011). However, these classical methods show limited performances. Even though neural networks may guarantee a fast response, the performance of control fails along the system variation.

Moreover, fuzzy logic approaches have been widely applied and have presented better effectiveness (Bahraminejad et al. 2014; Jerbi et al. 2009; Simoes et al. 1997), but, the major problems are the strict theoretical analysis and the lack of stability.

A backstepping approach has been studied and developed to the control of the PMSG (Karabacak and Eskikurt 2012; Wang et al. 2013; Yang et al. 2014a). This technique provides a good performance result. Sliding mode control emerges also as a suitable option to deal with such complex system and it has been applied in several works. Lee et al. (2010) propose the sliding mode control scheme to maximize the generated power below the rated wind speed, Results demonstrated by research (Vu et al. 2013; Zhang et al. 2013) involving the use of SMC with PMSG continue to prove the strength of SMC as a viable strategy for effective control of synchronous machines

Although the positive attributes of SMC, the phenomenon known as chattering gives an understandable level of criticism. Because of the nonidealities in switching devices, the response of the system oscillates with high frequencies about the desired reference, known as the sliding surface which leads to low control accuracy and even damages of mechanical parts.

In order to face this undesirable phenomenon, the literature proposes different improvement techniques Such as the approach presented in Kachroo and Tomizuka (1996) which places a boundary layer around the switching surface such that the relay control is replaced by a saturation function. Another class of techniques is based on introducing high order sliding mode algorithms for speed control (Feng et al. 2012; Valenciaga and Puleston 2008). In Evangelista et al. (2013), the speed tracking was achieved using a super-twisting sliding mode control based on Lyapunov techniques.

From this point of view, The main objective of this paper is to study the control algorithms for a variable speed wind turbine based permanent magnet synchronous generator.

In order to achieve a maximum power capture efficiency for the system in safety conditions, a nonlinear control strategy based on backstepping controller and sliding mode controller has been proposed. Furthermore, a blade pitch angle controller is proposed to enhance system performances in high wind speed region.

The rest of the paper is organized as follow. Section 8.2 presents the system modeling. The control technique applied to the wind system is introduced in Sect. 8.3. The Control below rated wind speed: MPPT zone is presented in Sect. 8.4. Section 8.5 describes the control above rated wind speed (the pitch control). The transition between the two control regions is detailed in Sect. 8.6. Finally, some conclusion remarks are drawn in the last Section.

8.2 Modeling of the Wind Turbine System

8.2.1 Wind Turbine Modeling

Consider a horizontal axis wind turbine (HAWT). The potentially available power by the wind is defined as:

$$\displaystyle \begin{aligned} P_{w}=\frac{1}{2}\pi \rho R^{2} V^{3} \end{aligned} $$
(8.1)

where:

  • R denotes the blade radius of the WT(m)

  • ρ is the air density (1.25 kg/m in normal atmosphere)

  • V  is the wind speed (m/s)

However, this expression can only stand if the wind passes through the swept area of the wind turbine.

In 1919, A German physicist Albert Betz state that no more than 59% of the kinetic energy, contained in a steam tube that shares the same cross-section as the disc, can be converted to useful works.

Figure 8.2 presents a schematic of fluid flow which helps to contextualize the statement.

Fig. 8.2
figure 2

Schematic of fluid flow through a wind turbine

Full size image

Thus, a power coefficient term is introduced and can be understood as:

$$\displaystyle \begin{aligned} C_p=\frac{\mathrm{mechanical} \hspace{0.2cm} \mathrm{power}\hspace{0.2cm} \mathrm{captured}\hspace{0.2cm} \mathrm{by}\hspace{0.2cm} \mathrm{the}\hspace{0.2cm} \mathrm{wind} \hspace{0.2cm}\mathrm{turbine} }{\mathrm{maximum} \hspace{0.2cm}\mathrm{power} \hspace{0.2cm}\mathrm{available} \hspace{0.2cm}\mathrm{in} \hspace{0.2cm}\mathrm{the}\hspace{0.2cm} \mathrm{wind}} \end{aligned} $$
(8.2)

C p represents the performance of the wind turbine. It depends on the tip-speed ratio (TSR) λ and the pitch angle β which is the angle between the orientation of the blade and the wind velocity vector:

$$\displaystyle \begin{aligned} \begin{array}{rcl} C_{p} (\lambda,\beta) &\displaystyle =&\displaystyle 0.22\left(\frac{116}{\lambda_{i}}-0.4 \beta-5 \right)e^{\frac{\textstyle -12.5}{\textstyle\lambda_{i}}} \\ \frac{1}{\lambda_{i}} &\displaystyle =&\displaystyle \frac{1}{\lambda+ 0.08 \beta}- \frac{0.035}{\beta^{3}+1} \end{array} \end{aligned} $$
(8.3)

with

$$\displaystyle \begin{aligned} \lambda=\frac{\varOmega_t R}{V} \end{aligned} $$
(8.4)

where Ω t is the turbine speed

The nonlinear relation between C p, λ and β is presented in Fig. 8.3.

Fig. 8.3
figure 3

Aerodynamic power coefficient variation C p against the speed ratio λ and the pitch angle β

Full size image

It is obvious that C p is maximised when β =0 and it decreases with the increase of β. For a constant pitch angle, there is a unique peak of the curve corresponding to C pmax.

The aerodynamic torque is given by:

$$\displaystyle \begin{aligned} T_{m}=\frac{P_{m}}{\varOmega_{t}}=\frac{1}{2}\;\pi \;\rho \;C_{p} (\lambda,\beta)\; \frac{ R^{2} \; V^{3}}{\varOmega_{t}} \end{aligned} $$
(8.5)

8.2.2 PMSG Modeling

The mathematical model of the PMSG in the d-q reference is Kim et al. (2010):

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \left\{ \begin{array}{rcl} U_d&=&R_{s} I_{d}+L_d \dfrac{d i_d}{dt}-\varOmega_{e} \varPhi_{q } \vspace{1mm} \\ U_q&=&R_{s} I_{q}+L_q \dfrac{d i_q}{dt}+\varOmega_{e} \varPhi_{d} \end{array} \right. \end{array} \end{aligned} $$
(8.6)

where R s is the stator resistance. Φ d and Φ q are the d and q axis flux linkage, respectively:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{d} &\displaystyle =&\displaystyle L_{d} I_{d}+\varPhi_{m} \\ \varPhi_{q} &\displaystyle =&\displaystyle L_{q} I_{q} \end{array} \end{aligned} $$
(8.7)

Furthermore, consider L q = L d = L s denotes the inductance of the stator (a PMSG with a nonsalient pole is considered in this study).

8.3 Control Technique

Wind Turbine systems present intense nonlinearities, and are subjected to disturbances and parameter uncertainties. Such factors transform their control to a hard task.

Therefore, a high level control is often required in order to ensure a certain convergence of the system to the requested state condition and to operate at maximum power coefficient over a wide range of wind speeds.

In fact, wind turbines should be driven differently according to the speed of the wind.

Therefore, the WT generator needs to be controlled to operate in three different modes as shown in Fig. 8.4.

Fig. 8.4
figure 4

Power versus wind speed characteristic

Full size image

  • Parking Mode (I): The wind speed is lower than the cut-in speed which is (2 m/s) in this system, the wind turbine stays in a parking status and does not rotate.

  • MPPT (Maximum Power Point Tracking) mode (II): The system starts to work and generates electrical power. The MPPT is applied until arrived to the rated wind speed, (12.7 m/s), for this case-study system. The blade angle is usually controlled at zero degree to maximize the wind energy capture.

  • Constant power Mode (III): It is necessary to control the extracted power above rated wind value by adjusting properly the blade pitch angle of the wind turbine to keep the power at constant power region, as its name implies.

8.4 Control Below Rated Wind Speed: MPPT Zone

In this region, the wind speed is below the rated value. The objective of the controller is to maximize the wind energy capture and to achieve the Maximum Point Power Tracking (MPPT). For that, The tip speed ratio λ is set to its optimal value λ opt which contributes to the power coefficient peak C pmax. Therefore, the optimum rotor speed of the Wind turbine can be written as follows:

$$\displaystyle \begin{aligned} \varOmega_{opt}=\frac{\lambda_{opt} v}{R} \end{aligned} $$
(8.8)

Thus, the maximum power output of the wind turbine can be expressed as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} P_{max} &\displaystyle =&\displaystyle k_{opt} \varOmega_{opt}^{3} \\ k_{opt} &\displaystyle =&\displaystyle \frac{1}{2} C_{pmax} \rho \pi R^{2} \left(\frac{R}{\lambda_{opt}}\right)^{3} \end{array} \end{aligned} $$
(8.9)

In addition, to achieve the MPPT operation mode, the pitch angle is kept at zero degree to ensure a high efficiency of energy capture.

The optimum rotor speed given in Eq. (8.8) is considered as the speed reference of the PMSG. Consequently, by using a robust control technique the generator speed will reach its reference value in the static state, and then the MPPT control is achieved.

In this work, the control system proposed to command the wind turbine generator is the Field Oriented Control (FOC), which controls the torque indirectly by adjusting the stator currents. In this method, the torque angle is maintained at 90∘. The d-axis current is set to zero and then the stator current has only the q-axis component. Thus, the torque depends only on the q-axis stator current. This technique removes current cross coupling between the d and q axes components.

Based on the FOC technique, different controller design have been investigated in this work to the PMSG to optimize the wind turbine power output.

  • Proportional Integral (PI) control

  • backstepping control

  • Sliding mode control

Remark 1

For the control design, the following assumptions are required:

Assumption 1

Variables i q, i d and Ω are available.

Assumption 2

The reference speed Ω ref is determined referring to the MPPT algorithm.

Assumption 3

The d-axis reference current should be equal to zero i d = 0.

8.4.1 Vector Control Based PI Controlller

8.4.1.1 Controller Design

This technique is the most commonly applied algorithm for the PMSG control (Ayadi and Derbel 2017). It involves two control loops:

  • two inner current loops are used to adjust the generator currents i d and i q allowing the control of the flux and the torque, respectively.

  • an external mechanical loop in order to ensure the speed regulation.

Then, to improve the dynamic response, compensation voltage, Δ Uq and Δ Ud are added into the control law.

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varDelta_{Ud} &\displaystyle =&\displaystyle \varOmega_{e} i_q L_s \\ \varDelta_{Uq} &\displaystyle =&\displaystyle \varOmega_{e} i_q L_s+\varOmega_{e} \varPhi_{m} \end{array} \end{aligned} $$
(8.10)

  • d-axis current controller design

The control of this component aims to keep the stator flux constant. Its reference value is set to zero.

$$\displaystyle \begin{aligned} \frac{i_d}{U_d}=\frac{\frac{1}{R_s}}{1+s \frac{L_d}{R_s}} \end{aligned} $$
(8.11)

The PI transfer’s function is:

$$\displaystyle \begin{aligned} G(s)= k_{d} \left(\frac{1+\tau_d s}{\tau_d s}\right) \end{aligned} $$
(8.12)

Based on the compensation pole method, the synthesis of this PI can be determined \(\tau _d=\frac {L_d}{R_s}\), \(K_d =\frac {R_s^2}{L_d}\), and the closed loop transfer function between the actual and the desired direct current is:

$$\displaystyle \begin{aligned} F_d(s)= \frac{1}{1+s \frac{L_s}{R_s}} \end{aligned} $$
(8.13)

  • q-axis current controller design

The control of the quadrature current i q affects directly the electromagnetic torque. The reference value of i q is determined from the speed control loop. The control law is implemented in the same way as the d-axis current controller yielding: \(\tau _q =\frac {L_s}{R_s}\) and \(K_q =\frac {R_s^2}{L_s}\).

  • Speed control loop

The reference value of this loop is the optimal speed Ω opt determined based on the MPPT strategy Eq. (8.8). The transfer function between Ω r and i q is given by:

$$\displaystyle \begin{aligned} \frac{i_q}{\varOmega_{r}}= \frac{\frac{3}{2} p \varPhi_{m}}{f+sJ } \end{aligned} $$
(8.14)

The PI transfer’s function is:

$$\displaystyle \begin{aligned} G_{\varOmega}(s)= k_{\varOmega} \left(\frac{1+\tau_{\varOmega} s}{\tau_{\varOmega}s}\right)\end{aligned} $$
(8.15)

Thus, the closed-loop transfer function is:

$$\displaystyle \begin{aligned} F_{\varOmega}(s)= \frac{1+\tau_{\varOmega}s}{1+ (\tau_{\varOmega}+\frac{f}{\frac{3}{2}p \phi_m K_{\varOmega}})s+\frac{J}{\frac{3}{2}p \phi_m K_{\varOmega}}s^2}\end{aligned} $$
(8.16)

The output of the PI represents the quadrature reference current \(\bar {i}_q\).

8.4.1.2 Simulation Results

Results have been presented, using numerical simulations carried under the Matlab-SIMULINK tool to test the control strategy and to evaluate the performance of the system.

Characteristics of the turbine and the Permeant Magnetic Synchronous Machine are presented in Table. 8.1.

Table 8.1 Turbine and PMSG parameters
Full size table

System simulation has been performed considering an aleatory wind profile to evaluate the behavior of the system similar to real conditions.

As shown in Fig. 8.4, for different regions of the wind speed, there is a specific control strategy. Therefore in this part, The wind speed will be limited to (11.5 m/s) as we are interested in the control below rated wind speed region(II).

  • Figure 8.5a presents the wind speed profile.

    Fig. 8.5
    figure 5

    wind speed profile

    Full size image

  • Figure 8.5b shows that the power coefficient C p is maintained close to its maximum value C pmax = 0.41. Thus, the Maximum Power Point Tracking MPPT has been achieved.

  • The system response under PI is shown in Fig. 8.6.

    Fig. 8.6
    figure 6

    Simulation results of the FOC based PI controller. (a): rotational speed, (b): Speed error, (c):direct current, (d): direct current error, (e):quadrature current, (f):quadrature current error

    Full size image

    Figure 8.6a shows the rotational speed response. It converges to its reference track which is supplied from the Maximum Power Point Tracking (MPPT) controller. Figure 8.6b presents the rotational speed error which exceeds the 0.2(rad/s). The direct and the quadrature currents are shown in Fig. 8.6c, e respectively. It is obvious from Fig. 8.6d, f that current errors present a considerable distorted values due to the nonlinear characteristics of the system

This control laws gives good dynamic response of the speed tracking and remarkable rejection of disturbances.

However, it should be noted that it is better to minimize as possible the tracking error, hence we propose two non-linear regulators namely the backstepping control and the sliding mode control in the sequel.

8.4.2 Backstepping Controller

8.4.2.1 Controller Design

This control approach is designed in such a way it keeps the same general structure of the vector control while ensuring at the same time the regulation and the limitation of the currents. The objective of the nonlinear backstepping controller is to track the speed of PMSG with the choice of appropriate regulated variables (Ayadi and Derbel 2017). Based on the PMSG model given in Eq. (8.6), The control design can be determined by following three steps as shown in Fig. 8.7.

Fig. 8.7
figure 7

Internal structure of the backstepping controller block

Full size image

  • Step 1: Control design based on rotational speed dynamics:

The speed error is:

$$\displaystyle \begin{aligned} e_{\varOmega}= \bar{\varOmega}_{r}-\varOmega_{r}\end{aligned} $$
(8.17)

The error dynamics derived can be obtained as:

$$\displaystyle \begin{aligned} \dot{e}_{\varOmega}= \dot{\bar{\varOmega}}_{r}-\frac{T_m}{J}+\frac{3 p}{2 J} \varPhi_{m} iq+\frac{B}{J} \varOmega_{r}\end{aligned} $$
(8.18)

Consider the following Lyapunov function candidate:

$$\displaystyle \begin{aligned} V_{\varOmega}= \frac{1}{2}e_{\varOmega}^{2} \end{aligned} $$
(8.19)

Its derivative is:

$$\displaystyle \begin{aligned} \dot{V_{\varOmega}}= e_{\varOmega}\dot{e}_{\varOmega}= e_{\varOmega} \left(\dot{\bar{\varOmega}}_{r}-\frac{T_m}{J}+\frac{3 p}{2 J} \varPhi_{m} iq+\frac{B}{J} \varOmega_{r}\right) \end{aligned} $$
(8.20)

The direct and quadrature current i d and i q are chosen as virtual control elements:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{lll} \bar{i}_d =0\hfil ~~~~~~~~~~~~ \vspace{2mm}\\ \bar{i}_q = \dfrac{2 J}{3 p \varPhi_{m}} \left(-\dot{\bar{\varOmega}}_{r}+\frac{T_m}{J}-\frac{B}{J} \varOmega_{r}- K_{\varOmega} e_{\varOmega}\right) ~~~~~~~~~~~~~~ \vspace{2mm} \end{array}\right. {} \end{aligned} $$
(8.21)

where K Ω > 0

Thus:

$$\displaystyle \begin{aligned} \dot{V_{\varOmega}}= -K_{\varOmega} e_{\varOmega}^{2} \end{aligned} $$
(8.22)

  • Step 2:Current components control design

The current error can be determined as:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} e_d &\displaystyle =&\displaystyle \bar{i}_d-i_d \\ e_q &\displaystyle =&\displaystyle \bar{i}_q-i_q \end{array} \end{aligned} $$
(8.23)

The error dynamics derived from Eqs. (8.18), (8.21) and (8.23) are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \dot{e}_d &\displaystyle =&\displaystyle \frac{R_{s}}{L_s}i_{d}-p i_q \varOmega_{r}-\frac{1}{L_s} U_d \\ \dot{e}_q &\displaystyle =&\displaystyle \frac{2 J}{3 p \varPhi_{m}} \left(-\ddot{\bar{\varOmega}}_{r}-\frac{B}{J}\dot{\varOmega}_{r}-K_{\varOmega} e_{\varOmega}\right)+\frac{R_{s}}{L_s}i_{q}+p\left(i_d+\frac{\varPhi_{m}}{L_s}\right )\varOmega_{r}-\frac{1}{L_s} U_q \\ \dot{e}_{\varOmega} &\displaystyle =&\displaystyle -\frac{3 p \varPhi_{m}}{2 J} e_q- K_\varOmega e_\varOmega \end{array} \end{aligned} $$

  • Step 3: Control laws design

The Lyapunov function is determined as:

$$\displaystyle \begin{aligned} V_2=\frac{1}{2}(e^{2}_{\varOmega}+e^{2}_d+e^{2}_q) \end{aligned} $$
(8.24)

Its time derivative is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \dot{V}_2 &\displaystyle =&\displaystyle (e_{\varOmega} \dot{e}_{\varOmega}+e_d \dot{e}_d+e_q \dot{e}_q) -K_{\varOmega_{r}} e^2_{\varOmega_{r}} -K_d e^2_d-K^2_q e_q- e_{\varOmega}\frac{ 3 p \varPhi_{m}}{2 J}e_q \\ &\displaystyle &\displaystyle +e_q\left[\frac{2 J}{3 p \varPhi_{m}} \left(-\ddot{\bar{\varOmega}}_{r}-\frac{B}{J}\dot{\varOmega}_{r}-K_{\varOmega} e_{\varOmega}\right) +\frac{R_{s}}{L_s}i_{q}+p(i_d+\frac{\varPhi_{m}}{L_s} )\varOmega_{r}\right. \\ &\displaystyle &\displaystyle \hspace{9mm}-\frac{1}{L_s} U_q+K_q e_q\left] +e_d\left[\frac{R_{s}}{L_s}i_{d}-p i_q \varOmega_{r}-\frac{1}{L_s} U_d+K_d e_d\right]\right. \end{array} \end{aligned} $$
(8.25)

The control inputs which stabilize The current tracking errors dynamics are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \bar{v}_d &\displaystyle =&\displaystyle R_{s}i_{d}-L_s p i_q \varOmega_{r}+{L_s} K_d e_d \end{array} \end{aligned} $$
(8.26)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \bar{v}_q &\displaystyle =&\displaystyle \frac{2 J L_s}{3 p \varPhi_{m}} \left(-\ddot{\bar{\varOmega}}_{r}-\frac{B}{J}\dot{\varOmega}_{r}-K_{\varOmega} e_{\varOmega}\right)+R_{s}i_{q}+p(i_d L_s+\varPhi_{m} )\varOmega_{r}+K_d L_s e_d \end{array} \end{aligned} $$

This choice yields:

$$\displaystyle \begin{aligned} \dot{V}_2=-K_{\varOmega} e^2_{\varOmega_{r}} -K_d e^2_d-K_q e^2_q\leq0 \end{aligned} $$
(8.27)

where K d and K q are positive gains.

8.4.2.2 Simulation Results

The same wind speed profile is applied in this part with varying degrees of wind speed between (8 m/s) and (11.5 m/s).

  • The system response under PI controller and nonlinear backstepping control has been presented in Fig. 8.8.

    Fig. 8.8
    figure 8

    Simulation results

    Full size image

    Figure 8.8a presents the rotational speed response which converges perfectly to its reference track. Figure 8.8b shows the speed error. Its is neglected for the backstepping control compared to PI controller. Figures 8.8c, e illustrate the direct and the quadrature currents, respectively. The evolution of the currents errors (Fig. 8.8d, f) shows that the backstepping control has a good dynamic response.

8.4.3 Sliding Mode Control

8.4.3.1 Controller Design

The sliding mode control has proved to be an efficient technique able to cope with aforementioned complex characteristics. In this context, this technique is applied in this section to design a robust controller for nonlinear multi-input multi-output permanent magnet synchronous generator based WECS. The controller design is ensured by the following steps.

  1. 1.

    Sliding surfaces:

    Based on the system model, the sliding surfaces are to be defined as:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_d(t) &\displaystyle =&\displaystyle e_d(t)+\lambda_1 \int e_d(t)dt {} \end{array} \end{aligned} $$
    (8.28)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_q(t) &\displaystyle =&\displaystyle e_q(t)+\lambda_2 \int e_q(t)dt{} \end{array} \end{aligned} $$
    (8.29)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_{\varOmega_r}(t) &\displaystyle =&\displaystyle e_{\varOmega_r}(t)+\lambda_3 \int e_{\varOmega_r}(t)dt {} \end{array} \end{aligned} $$
    (8.30)

    where e d(t) = i d(t) − i dref(t), e q(t) = i q(t) − i qref(t) and \(e_{\varOmega _r}(t)=\varOmega _{r}(t)-\varOmega _{rref}(t)\).

    The integral action has been included to overcome the state error and to improve the sliding surface where λ 1, λ 2, λ 3 are the integral gains.

  2. 2.

    Reachability:

    The reachability condition for Eqs. (8.28), (8.29) and (8.30) are defined respectively as:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_d(t)\dot{S}_d(t) &\displaystyle <&\displaystyle 0 {} \end{array} \end{aligned} $$
    (8.31)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_q(t)\dot{S}_q(t) &\displaystyle <&\displaystyle 0 {} \end{array} \end{aligned} $$
    (8.32)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_{\varOmega_r}(t) \dot{S}_{\varOmega_r}(t){}&\displaystyle <&\displaystyle 0 \end{array} \end{aligned} $$
    (8.33)
  3. 3.

    d-axis current control design

    The control of i d component current aims to keep the stator flux constant. Its reference value is set to zero.

    From Eq. (8.21), the inequality Eq. (8.31) can be rewritten as:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_d(t)\left[\left(\lambda_1-\frac{R_{s}}{L_s}\right)i_{d}+p i_q \varOmega_{r}+\frac{1}{L_s} U_d\right] &\displaystyle <&\displaystyle 0 \end{array} \end{aligned} $$
    (8.34)

    The d-axis control law is given by:

    $$\displaystyle \begin{aligned} U_d(t)=U_{deq}(t)+\varDelta U_d \end{aligned} $$
    (8.35)

    with the equivalent controlU deq is:

    $$\displaystyle \begin{aligned} U_{deq}(t)=(R_s-\lambda_1 L_s)i_d-p i_q \varOmega_r L_s \end{aligned} $$
    (8.36)

    The switching control ΔU d is defined as:

    $$\displaystyle \begin{aligned} \varDelta U_d =K_d \mathrm{sign}[S_d(t)] \end{aligned} $$
    (8.37)

    where K d is a positive constant

  4. 4.

    q-axis current control design

    Based on the system model and following the similar method, Eq. (8.32) becomes:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_q(t) \left[\left(\lambda_2+\frac{R_{s}}{L_s}\right)i_{q}-p\left(i_d+\frac{\varPhi_{m}}{L_s}\right)\varOmega_{r}+\frac{1}{L_s} U_q +\lambda_2 iq_{ref}\right]&\displaystyle <&\displaystyle 0 \end{array} \end{aligned} $$

    Denoting the control law as:

    $$\displaystyle \begin{aligned} U_q(t)=U_{qeq}(t)+\varDelta U_q \end{aligned} $$
    (8.38)

    The equivalent control can be given as:

    $$\displaystyle \begin{aligned} U_{qeq}=(R_{s}+L_s \lambda_2)i_{q}+p(L_s i_d +\phi_m)\varOmega_{r}-\lambda_2 L_s iq_{ref}-L_s \frac{diq_{ref}}{dt} \end{aligned} $$
    (8.39)

    where i qref is a dynamic value that will be determined as a resulting output of the rotational speed control.

    The switching portion of the U q(t) can be expressed by:

    $$\displaystyle \begin{aligned} \varDelta Uq=K_q \mathrm{sign}[S_q(t)] \end{aligned} $$
    (8.40)

    where K q is a positive constant

  5. 5.

    Rotational speed dynamics control

    This controller should ensure that the rotational speed. It is driven to its reference determined by the MPPT algorithm. Considering the rotational speed motion equation, the inequality Eq. (8.33) becomes:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} S_{\varOmega_r}(t) \left[\frac{T_m}{J}-\frac{3}{2J} p\varPhi_{m}i_q+\left(\lambda_3-\frac{B}{J}\right) \varOmega_{r}-\lambda_3 \varOmega_{ref}\right]&\displaystyle <&\displaystyle 0 \end{array} \end{aligned} $$
    (8.41)

    The control variable for the rotational speed controller is the quadrature axis reference current which is designed as:

    $$\displaystyle \begin{aligned} i_{qref}(t)=i_{qeq,ref}(t)+\varDelta i_{qref} \end{aligned} $$
    (8.42)

    The equivalent control law is given as:

    $$\displaystyle \begin{aligned} i_{qref}=\frac{2}{3 p \phi_m}\left[T_m+(\lambda_3J-B)\varOmega_r-\lambda_3\varOmega_{ref}\right]{} \end{aligned} $$
    (8.43)

    It then follows that:

    $$\displaystyle \begin{aligned} \varDelta i_{qref}=K_{iq} \mathrm{sign}[S_{\varOmega_r}(t)] \end{aligned} $$
    (8.44)

    where K iq is a positive constant

In order to reduce the chattering effect, a smooth control discontinuity is introduced around the switching surface. The sign [S(t)] is replaced by sat[S(t),Δ] which can be expressed as:

$$\displaystyle \begin{aligned} \mathrm{sat} [S(t)] = \left| \begin{array}{ll} \frac{S(t)}{\varDelta} & \mathrm{ if } ~~ |S(t)| ~~\leq ~~\varDelta \\ \mathrm{sign}(S(t)) ~~ ~~ & \mathrm{otherwise} \end{array} \right. \end{aligned} $$
(8.45)

where Δ is the boundary layer thickness.

8.4.3.2 Simulation Results

The system response under the Sliding Mode concept has been presented in Fig. 8.9.

Fig. 8.9
figure 9

Simulation results of the Sliding mode strategy

Full size image

The rotational speed Ω r(t) is shown in Fig. 8.9a. The second result shown is that of i d(t). As it can be seen by Fig. 8.9c, the d-axis current accurately tracks the reference value i dref = 0. Figure 8.9e. shows the actual value of i q(t), accurately tracking the defined reference.

8.5 Control Above Rated Wind Speed: Pitch Control

8.5.1 Introduction

The key part of a variable-speed wind turbine is the pitch system. Its main purpose is to keep the generated power constant above the rated wind speed.

In fact, when the wind speed becomes larger than the rated value and the MPPT algorithm is still applied, the power generated by the system will exceed the optimal power if the blade angle β stays fixed at zero degrees.

This will make the power devices and the generator work in a higher zone than optimum output, which is harmful to the mechanical system if sustained for a period of time.

Based on this concern, a control system for the regulation of the pitch angle according to different wind conditions is required for the wind turbine.

Small changes in the blade angle can have dramatic effects on the output power.

The advantages of the pitch control system might be summarized as follows:

  1. 1.

    Optimize the output power of the wind turbine. Indeed, to give the maximum power in partial load region, the pitch setting should be at its optimum value

  2. 2.

    Prevent input mechanical power to exceed the design limits. This controller provides a good regulation of the aerodynamic power and the loads produced by the rotor.

  3. 3.

    Minimize the fatigue loads of the turbine mechanical components. The design of the controller must take into account the load.

Thus, the blade pitch angle control should have a good dynamic quality and a strong robustness.

Several works on pitch control have been done to improve the quality of the generated power. For example, a gain scheduling controller, proposed in Lescher et al. (2005), changes the controller gain with the variation of the wind speed. However, the practical implementation of the gain scheduling is very difficult because the wind speed is usually measured on the tower and does not represent the wind speed at the turbine plant. Disturbance accommodating control (DAC) has been developed in Stol et al. (2000, 2003), but it presents a large estimation error when the system operates far away from the rated wind speed. H ∞ controllers for blade pitch control and electromagnetic torque control have been used in Rocha et al. (2003). However, this controller has not been experienced on a nonlinear turbine model.

Based on the analysis of the above studies, we propose two types of controllers to solve the variable pitch control problem of a direct-drive PMSG wind turbine (Ayadi et al. 2017):

  • Pitch Control based on a Proportional Integrator controller

  • Pitch Control based on a Sliding Mode controller

8.5.2 System Description

The blade pitch control system is the key part of a variable speed wind turbine. It acts directly on the system responses for different wind speed zones (Fig. 8.10).

Fig. 8.10
figure 10

Schematic illustration of the Kinematics of the WT

Full size image

To regulate the blade angle, the power deviation from its reference value is used.

An electromechanical system called actuator is then used to put the blade angle into the desired position. It can be modeled as a first-order system as Hwas and Katebi (2012):

$$\displaystyle \begin{aligned} G(s)=\frac{k_0}{1+\tau s} \end{aligned} $$
(8.46)

k 0 is the proportional gain and τ is the time constant.

According to industrial recommendations, it is necessary to include a pitch rate adjusted to 10∘∕s

8.6 Transition Between the Two Control Regions

8.6.1 Switched Wind Turbine System

Variable speed wind turbines operate within a large range of wind speeds. During the power generation and depending on the prevailing wind speed, the wind turbine switches between two operation modes as shown in Fig. 8.4: the low wind speed region (also called Region II) where the control objective is to capture the maximum power from the wind and the high wind speed region (also called Region III) where the control aim is to limit the output power to the required power.

The control of a variable speed wind turbine is usually achieved based on two distinct control laws for Regions (II) and (III), respectively. The switching or called also transition between these two regions cause undesirable effects such as vibrations in drive train, tower and blades (Pao and Johnson 2009) which cause system fatigue and premature failure.

Therefore, it is necessary to develop a control algorithm to smooth out the undesirable effects of the switching actions and also to stabilize the switching operation.

The synthesis of the blade angle controller is divided typically into two zones according to the wind speed value:

  • Partial load zone: v < v ref →β = β ref = 0

  • Full load zone: v ≥ v ref → β changes with the wind variation to keep P = P opt

There are usually two controllers for the variable-speed wind turbines which are cross-coupled each other, shown as in Fig. 8.11.

Fig. 8.11
figure 11

Structure of a model of variable-speed wind turbine

Full size image

In order to smooth the wind power fluctuations in the intermediate zone, a fuzzy logic controller has been investigated.

8.6.2 Simulation Results

To validate the stability of the system when it switches between Region (II) and Region (III) modes, simulations have been performed on a system with the following conditions:

  1. 1.

    Maximum Power Coefficient (C pmax) = 0.4109

  2. 2.

    Rated wind speed V m = 11.7

  3. 3.

    Nominal Demand Power (P max) = 2.5 kW

Figure 8.12a presents the wind speed profile which involves the two operational areas, i.e., the low wind speed area (V <  11.7 m/s) and the high wind speed area (V  ≥ 11.7 m/s).

Fig. 8.12
figure 12

Simulation results in full range of operation

Full size image

The power characteristic is shown in Fig. 8.13b. The turbine starts operating when the wind speed exceeds cut-in wind speed 3 m/s. In this region (II), The MPPT algorithm and the torque control come into action with a constant pitch angle.

Fig. 8.13
figure 13

Simulation in the transition region

Full size image

When the wind speed exceeds its nominal value (region III), the control objective shifts from maximizing the power capture to regulate the power to the turbine rated output.

Figure 8.12c shows the pitch angle variation. Below the rated wind speed the blade pitch angle is set at 0. It is the optimal value that allows the turbine to extract the maximum energy from the incident wind. Otherwise, the pitch control is active: the angle changes with the variations of the wind to avoid over rated power.

Figure 8.12d presents a zoomed in section of Fig. 8.13b. It is obvious that Between the high and the low wind speed region, the curve of the output power presents a noticeable fluctuation caused by the transition between the two regions which causes system fatigue and premature failure.

As a solution, a fuzzy logic controller has been applied with the aim of smoothing the wind power fluctuations in the intermediate zone. Figure 8.13a presents the wind speed profile with varying degrees. Figure 8.13b presents the power coefficient C p. It can be observed that the C p curve is maintained close to its maximum value C pmax = 0.41 which proves that the MPPT has been achieved. In region (III) as the power coefficient depends on the blade pitch angle, it varies with the blade variations.

Figure 8.13c presents the generated power for the 2 control zones: It is remarkable that the fluctuation between the intermediate zone has been eliminated. The wind speed moves from zone to another fluently. The variation of the pitch angle is illustrated in Fig. 8.13d. The pitch angle controller shows a perfect capability of giving to the actuator the right angle demand in different wind speed zones. The rotational speed is presented in Fig. 8.13e, (in region II) the speed is varying to optimal power extraction, overrated wind speed, the speed control input is considered as its maximum value.

8.7 Conclusion

This chapter discusses the control systems used for a variable speed wind turbine equipped with PMSG. In the first part, a control algorithm has been synthesized to extract the maximum of the power based on two nonlinear control techniques namely the backstepping controller and the sliding mode controller. Comparative studies between these algorithms have been presented. Then, above rated wind speed, a pitch angle regulation has been investigated to keep the generated power at the designed limit.

Finally, the transition between the two control regions has been discussed to avoid the power fluctuation.