Keywords

1 Introduction

Zinc oxide (ZnO) is a semiconductor with a wide band-gap in the near UV at 3.36 eV and large exciton binding energy. These characteristics make this material interesting for many applications, such as solar cells [1], optical coating [2], and gas sensors [3]. The role of the particle size, doping, impurities, and morphology is very important to these applications, which has driven researchers to focus on the synthesis of doped and pure nanocrystalline ZnO in recentyears. Doping semiconductor nanostructures in order to control their physical properties is an active field of research related to the development of nanotechnology applications. However, ZnO can be doped by many elements, such as S [4], N [5], Cu [6], Al [7], Ag [8], Eu [9] and Mg [10], to meet the demands of different applications. Among various dopants, Al can be easily doped in the lattice of ZnO for its similar radius and electronic shell to Zn atom.

Various methods have been used for the preparation of ZnO nanoparticles, such precipitation method [11], sol gel processing [12] and mechanical milling [13]. The sol-gel has some advantages such low temperature synthesis, high purity, homogeneity, repeatability and particularly its cheapness and simplicity. In this work, a simple sol gel method was used to prepare ZnO nanoparticles. The effects of Al content on structural and morphological properties of the obtained nanopowders were investigated.

2 Experimental Methods

ZnO particles were prepared by sol-gel method using zinc acetate as the precursor. A 4.4g zinc acetate (Zn (CH3COO)2, 2H2O) in 100 ml (70 ml of distilled water+30 ml of ethanol), this solution will be noted (A). 2 g sodium hydroxide was dissolved in 100 ml (80 ml of distilled water+20 ml ethanol) (solution B). After heating the solution A to 50 °C, solution (B) was added drop wise with constant warm stirring. This would result in the appearance of turbidity in the obtained solution leading to the formation of ZnO in the form of gel. After the complete addition, the resulting solution was stirred overnight which was then filtered, washed with water and dried at 100 °C for 2 h, manually ground and calcined at 200 °C for 3 h in order to obtain pure ZnO. In order to obtain \( {\text{Zn}}_{{{\text{x}} - 1 }} {\text{Al}}_{\rm{x}} {\text{O}}_{\rm{x}} \) nanoparticles, an adequate amount of \( (\left( {{\text{Al}}_{2} {\text{SO}}_{4} } \right)_{3} ,18{\rm{H}}_{2} {\rm{O}}) \) with Al/Zn proportions of (0.00, 0.01, 0.02 and 0.05) are dissolved in required amount of ethanol, were added to the solution A along with solution B simultaneously. After stirring the solution overnight (ZnO-doped) was formed, which was filtered, washed with distilled water to remove the excessions and insoluble materials remaining in the product and dried at 100 °C for 2 h. The powdered material obtained was manually ground and calcined at 200 °C for 3 h.

The structure and crystallite size of pure ZnO and (AZO) were determined by X-ray diffraction (XRD) using Cu-Kα radiations \( (\lambda = 0.15406 \,nm) \) in 2θ range from 10° to 80°. SEM technique coupled with EDX was employed to determine the size and the chemical composition of the samples.

3 Results and Discussions

3.1 Structural Parameters

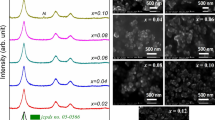
Figure 1 shows the XRD patterns of \( {\text{Zn}}_{{1 - {\text{x}}}} {\text{Al}}_{\rm{x}} {\text{O}}\left( {{\mathbf{x}}\% = {\mathbf{0,1,2,3, 5}}} \right) \), in the range of \( 2\uptheta = 10^\circ - 80^\circ \). They indicate the single phase formation with a hexagonal wurtzite structure for all samples. The three pronounced diffraction peaks at about \( 2\uptheta = 31.8^\circ , 34.5^\circ \) and \( 36.3^\circ \) are identified, respectively, as the \( \left( {1 0 0} \right),\left( {0 0 2} \right) \) and \( \left( {1 0 1} \right) \) peaks of ZnO [14, 15]. The hexagonal structure is not changed during the doping, but it can be seen from this Figure that the incorporation of \( Al^{3 + } \) ions affects the intensity of all peak, so it enhances the crystalline quality. For evaluating de preferred orientation of de samples, a texture coefficient will be used.

Fig. 1.
figure 1

XRD spectra of the undoped and Al doped ZnO nanoparticles for different doping contents

Full size image

The quantitative information concerning the preferential crystal orientation can be obtained from the texture coefficient, \( {\text{TC}} \), which can be defined as [16]:

$$ TC_{{\left( {hkl} \right)}} = {{\left( {\frac{{{\text{I}}_{{\left( {\text{hlk}} \right)}} }}{{{\text{I}}_{{0\left( {\text{hkl}} \right)}} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\text{I}}_{{\left( {\text{hlk}} \right)}} }}{{{\text{I}}_{{0\left( {\text{hkl}} \right)}} }}} \right)} {\left[ {\frac{1}{\text{N}}\sum\nolimits_{\text{n}} {\frac{{{\text{I}}_{{\left( {\text{hkl}} \right)}} }}{{{\text{I}}_{{0\left( {\text{hkl}} \right)}} }}} } \right]}}} \right. \kern-0pt} {\left[ {\frac{1}{\text{N}}\sum\nolimits_{\text{n}} {\frac{{{\text{I}}_{{\left( {\text{hkl}} \right)}} }}{{{\text{I}}_{{0\left( {\text{hkl}} \right)}} }}} } \right]}} $$
(1)

Where \( {\text{TC}}_{{\left( {\text{hkl}} \right)}} \) is the texture coefficient, \( {\text{I}}_{{\left( {\text{hkl}} \right)}} \) is the intensity of the XRD of the sample and n is the number of diffraction peaks considered. \( {\text{I}}_{{0\left( {\text{hkl}} \right)}} \) is the intensity of the XRD reference of the randomly oriented grains. If \( TC_{{\left( {hkl} \right)}} \approx 1 \) for all the \( \left( {hkl } \right) \) planes are considered, then the nanoparticles are with a randomly oriented crystallite similar to the JCPDS reference, while values higher than1 indicate the abundance of grains in a given \( \left( {hkl} \right) \) direction. Values \( 0 < TC_{{\left( {hkl} \right)}} < 1 \) indicate the lack of grains oriented in that direction. As \( TC_{{\left( {hkl} \right)}} \) increases, the preferential growth of the crystallites in the direction perpendicular to the \( \left\langle {hkl} \right\rangle \) plane is greater. In this analysis, three reflections are considered. From the Table 1, the \( \left( {{\mathbf{002}}} \right) \) orientation is the preferred growth direction for all \( Al \) content. This direction will be considered for the calculation of all physical parameters.

Table 1. \( \text{T}{\text{exture coefficient }}TC_{{\left( {hkl} \right)}} \) of as deposited \( {\text{Zn}}_{{1 - {\text{x}}}} {\text{Al}}_{\text{x}} {\text{O}} \) samples
Full size table

Indeed, the intensity of the preferred orientation \( \left( {0 0 2} \right) \) decreases gradually with increasing of Al content from 0% to 5%, as it is shown in Fig. 2, the width of this peak is also affected. Here, the \( Al^{3 + } \) ions (ion radius \( 0.53\, {\AA} \)) is smaller than \( Zn^{2 + } \) ions (ion radius 0.74 Å), so the increasing Al concentration will reduce the lattice constant of samples by substitution of \( Zn^{2 + } \) ions with \( Al^{3 + } \). The average crystallite size was estimated using Scherer’s formula.

Fig. 2.
figure 2

Evolution of the preferred orientation peak (002) with various Al contents.

Full size image
$$ D = K\lambda /\beta_{hkl} Cos\theta $$
(2)

Where D is the average crystallite size, K is a constant or shape factor and equal to 0.9, λ is the wavelength of the radiation (1.54056 \( {\AA} \) with CuKα radiation), \( \varvec{\beta}_{{\varvec{hkl}}} \) is the peak with at half maximum intensity and θ is the peak position. The average crystalline size was in the range of 15–37 nm. It decreases with increasing Al content \( in \,Zn_{1 - X} Al_{X} O \) nanoparticles. It may be due to the small grain growth of (AZO) nanoparticles as comprised with pure ZnO nanoparticles. The values of average crystallite size are listed in Table 3.

Owing to crystal imperfection and distortion, the strain induced in the samples was calculated by the formula [17]:

$$ \varvec{\varepsilon}= \frac{\varvec{\beta}}{{{\mathbf{4}}\varvec{tan\theta }}} $$
(4)

The calculated values are listedin Table 3 and plotted in Fig. 4. It clearly shows that the un-doped sample shows low lattice strain values than as the doped samples. Figure 4 clearly explains the influence of Al doping on lattice strain with respect to the crystal orientation of un-doped and Al doped samples. We note that the increase of strain leads to the reduction in the nanoparticles size.

To understand the effect of \( \varvec{Al } \) doping on lattice parameters of ZnO, the lattice parameters should be calculated for undoped and \( \varvec{Al } \) doped ZnO nanoparticles. Since ZnO lattice is wurzite structure with hexagonal shape, there are two latticeparameters a and c are exist and can be calculated from the following relations \( \left[ {18} \right] \):

$$ \varvec{d}_{{\left( {\varvec{hkl}} \right)}} = \left[ {\frac{{\mathbf{4}}}{{\mathbf{3}}}\left( {\frac{{\varvec{h}^{{\mathbf{2}}} + \varvec{kl} + \varvec{k}^{{\mathbf{2}}} }}{{\varvec{a}^{{\mathbf{2}}} }}} \right) + \frac{{\varvec{l}^{{\mathbf{2}}} }}{{\varvec{c}^{{\mathbf{2}}} }}} \right]^{{ - {\mathbf{1}}/{\mathbf{2}}}} $$
(5)

The lattice constant \( a \) for \( \left\langle {{\mathbf{100}}} \right\rangle \) lane is calculated by [18]:

$$ \varvec{a} =\varvec{\lambda}/\sqrt {{\mathbf{3}}\varvec{ }} \varvec{Sin\theta } $$
(6)

For the \( \left\langle {{\mathbf{002}}} \right\rangle \) plane, the lattice constant c is calculated by [18]:

$$ \varvec{c} =\varvec{\lambda}/\varvec{Sin\theta } $$
(7)

Where \( \lambda \) is the X-ray wavelength and \( d_{{\left( {\text{hkl}} \right)}} \) is the spacing between planes of given Miller indices \( h \), \( k \) and \( l \). Using the relation given in Eq. (4) and (5), the latticeparameters of un-doped and \( Al \) doped ZnO nanoparticles were calculated and are summarized in Table 2. Thus, \( Al \) doping does not cause any remarkable change in the wurtzite structure of ZnO. This may be due to the comparable ionic radii of Zn2+and \( Al^{3 + } \) which made the substitution of Zn2+easy with \( Al^{3 + } \) [19, 20] (Fig. 3).

Table 2. Structural parameters of \( {\text{Zn}}_{{1 - {\text{x}}}} {\text{Al}}_{\text{x}} {\text{O}} \)
Full size table
Fig. 3.
figure 3

Variation of crystallite \( \left( {\mathbf{D}} \right) \) and strain \( \left(\varvec{\varepsilon}\right) \) of \( {\mathbf{Zn}}_{{1 - {\mathbf{x}}}} {\mathbf{Al}}_{{\mathbf{x}}} {\mathbf{O}} \) with different conent

Full size image

Residual stress is possible at the time of crystal growth. Moreover, the doping process may influence the residual stress of bare materials. So it has to be addressed for clear understanding the influence of doping on the change in residual stress of ZnO in this study. In this paragraph, only the effect of the doping is studied. \( \varvec{\varepsilon Y} =\varvec{\sigma} \)

Where \( Y \) is the Young’s modulus. For a hexagonal crystal, Young’s modulus is given by the following relation [21]:

$$ \varvec{Y} = \frac{{\left[ {\varvec{h}^{{\mathbf{2}}} + \frac{{\left( {\varvec{h} + {\mathbf{2}}\varvec{k}} \right)^{{\mathbf{2}}} }}{{\mathbf{3}}} + \left( {\frac{{\varvec{al}}}{\varvec{c}}} \right)^{{\mathbf{2}}} } \right]^{{\mathbf{2}}} }}{{\varvec{s}_{{{\mathbf{11}}}} \left( {\varvec{h}^{{\mathbf{2}}} + \frac{{\left( {\varvec{h} + {\mathbf{2}}\varvec{k}} \right)^{{\mathbf{2}}} }}{{\mathbf{3}}}} \right)^{{\mathbf{2}}} + \varvec{s}_{{{\mathbf{33}}}} \left( {\frac{{\varvec{al}}}{\varvec{c}}} \right)^{{\mathbf{4}}} + \left( {{\mathbf{2}}\varvec{s}_{{{\mathbf{13}}}} + \varvec{s}_{{{\mathbf{44}}}} } \right)\left( {\varvec{h}^{{\mathbf{2}}} + \frac{{\left( {\varvec{h} + {\mathbf{2}}\varvec{k}} \right)^{{\mathbf{2}}} }}{{\mathbf{3}}}} \right)\left( {\frac{{\varvec{al}}}{\varvec{c}}} \right)^{{\mathbf{2}}} }} $$
(8)

Where \( S_{11} = 7.858.10^{ - 12} ,\,S_{13} = - 2.206.10^{ - 12} ,\,S_{33} = 6.940.10^{ - 12} \),

\( S_{44} = 23.57.10^{ - 12} m^{2} /N \) respectively [22] are the elastic compliances of ZnO with values. Young’s modulus for \( {\text{Zn}}_{{1 - {\text{x}}}} {\text{Al}}_{\text{x}} {\text{O}} \) was calculated and reported in Table 3.

Table 3. Crystallite size, strain, dislocation density and stress of as deposited Zn1-XMgxO samples
Full size table

In the W-H method, the peak width from crystallite size does not follow a \( 1/\cos\uptheta \) dependency as in the Scherer’s equation but instead varies with \( \tan\uptheta \). This fundamental difference allows for a separation of reflection broadening when both micro structural causes – small crystallite size and micro strain- occur together. The different approaches presented in the following assume that size and strain broadening are additive components of the total integral breadth of a Bragg peak [23]. Addition of the Scherer equation and \( \varvec{\varepsilon}=\varvec{\beta}/{\mathbf{4}}\tan \varvec{\theta } \) results in following equations:

$$ \varvec{\beta cos\theta } = \left( {\frac{{\varvec{k\lambda }}}{\varvec{D}}} \right) + {\mathbf{4}}\varvec{\varepsilon sin\theta } $$
(10)

Equation (10) represents the uniform deformation model (UDM), where the strain was assumed to be uniform in all crystallographic directions, thus considering the isotropic nature of the crystal, where the material properties are independent of the direction along which they are measured.

In the Uniform Stress Deformation Model, USDM, the generalized Hook’s law referred to the strain, keeping only the linear proportionality between the stress and strain, i.e., σ = \( Y \). Here, the stress is proportional to the strain, with the constant of proportionality being Young’s modulus, denoted by Y. In this approach, the Williamson-Hall equation is modified by substituting the value of ε in Eq. (11), we get σ

$$ {\varvec{\upbeta}}{\mathbf{cos}}{\varvec{\uptheta}} = \left( {\frac{{{\mathbf{k\lambda }}}}{{\mathbf{D}}}} \right) + \left( {\frac{{{\mathbf{4\sigma }}{\mathbf{sin}}{\varvec{\uptheta}}}}{{\mathbf{Y}}}} \right) $$
(11)

The strain can be calculated in the same way as \( \varvec{\varepsilon} \).

For an elastic system that follows Hooke’s law, the energy density (\( \varvec{u} = (\varvec{\varepsilon}^{2} \varvec{Y})/2 \))

can be calculated using another model called the Uniform Deformation Energy Density Model, UDEDM:

$$ {\varvec{\upbeta}}{\mathbf{cos}}{\varvec{\uptheta}} = \left( {\frac{{{\mathbf{k}}{\varvec{\uplambda}}}}{{\mathbf{D}}}} \right) + \left( {{\mathbf{4}}{\mathbf{Sin}}{\varvec{\uptheta}}\left( {\frac{{{\mathbf{2}}{\mathbf{u}}}}{{\mathbf{Y}}}} \right)^{{{\mathbf{1}}/{\mathbf{2}}}} } \right) $$
(12)

For UDM model, the plot of \( \varvec{\beta cos\theta } \) along the y-axis, \( {\mathbf{4}}\varvec{sin\theta } \) along the x-axis and with a linear fit to the data, the crystalline size \( \varvec{D} \) was estimated from the y-intercept, and the \( \varvec{strain}\,\varvec{\varepsilon} \), from the slope of the fit. In order to determine \( \sigma \) and u, the same method will be used for the UDSM AND UDEM models by keeping \( \varvec{\beta cos\theta } \) on the y-axis and \( \left( {{\mathbf{4}}{\mathbf{sin}}{\varvec{\uptheta}}/{\mathbf{Y}}} \right) \), \( {\mathbf{4}}{\mathbf{sin}}{\varvec{\uptheta}}\left( {{\mathbf{2}}/{\mathbf{Y}}} \right)^{{{\mathbf{1}}/{\mathbf{2}}}} \) along the x-axis respectively. The corresponding plots of the three models are shown in Fig. 4:

Fig. 4.
figure 4

UDM, USDM and UDEDM plots of \( \varvec{Zn}_{0.99} \varvec{Al}_{0.01} \varvec{O} \) sample

Full size image

Table 4 Summarizes the geometric parameters of ZnO nanoparticles obtained from Scherer’s formula, various modified forms of W-H analysis. By comparing the values of average crystallite size obtained from UDM, UDSM, and UDEDM, it was found that the values are similar, implying that the inclusion of strain in various forms has a very small effect on the average crystallite size of ZnO nanoparticles. However, the average crystallite size obtained from Scherer’s formula and W-H analysis shows a small variation; this is because of the difference in averaging the particle size distribution. The values of strain from each model are calculated by considering Young’s modulus \( Y \) is equal 127 GPa.

Table 4. The geometric parameters of Zn1-XAlxO samples
Full size table

3.2 Quantitative Results of al Doped ZnO from EDX Analysis

The SEM photographs of the samples reported in Fig. 5 revealed that the crystallites are of the nanometer size.

Fig. 5.
figure 5

SEM images of Al-doped ZnO powders with different doping amount. (a) x = 0, (b) x = 0.01, (c) x = 0.02 (d) x = 0.03 (e) x = 0.05

Full size image

The chemical compositions were analyzed by energy dispersive spectroscopy (EDX). Figure 6 shows the EDX spectrum obtained from pure ZnO powders, where only Zn and O are detected, while the presence of \( Al \) in the dopedZnO. From Table 5, the Atom% for Al increases with the increase of Al doping.

Fig. 6.
figure 6

EDX Spectra of Zn1-xAlxOsamples (a) x = 0, (b) x = 0.01, (c) x = 0.02 (d) x = 0.03 (e) x = 0.05

Full size image
Table 5. Quantitative results of Al doped ZnO from EDX analysis
Full size table

SEM results showed that the particle size was decreased with the doping of Aluminum.

4 Conclusion

Un-doped and Al doped ZnO nanoparticles were synthesized by a simple sol-gel method. The results of the XRD showed that the average particle size varies with the Al contents. The average values of crystallite size obtained from UDM, UDSM, and UDEDM are almost similar, which indicate the inclusion of strain in various forms of W–H analysis has a very small effect on the average crystallite size. The SEM confirms the nanostructure of the powders synthesized by sol gel, the EDX measurement indicates the incorporation of Al in the doped samples.