Keywords

1 Introduction

Contemporary business environment is highly challenging due to factors like uncertainty, globalization, and competition. Engaging new customers and retaining existing customers require a full proof strategy. The margin of error in given times is so low that a slight compromise with the strategy may result in loss to the business.

In order to engage new customers, firms often release offers and discounts. These discounts can be observed very frequently. Let it be online stores or offline stores, every firm comes up with discounts and offers every now and then. These offers and discounts attract customers to visit the stores or online web portals. These mobilized customers are termed as encouraged arrivals in this paper. At times customers also get attracted toward a firm once they see that lot of people are engaged in service with the particular firm already. Since a high volume of customers ensures a better quality, affordable price, or service, therefore, an arriving customer may get attracted toward a firm where there are customers already exist in large volumes. For example, in a healthcare facility, a large patient base ensures better doctors, better facilities, better treatment at affordable cost, or better service. This phenomenon was termed as reverse balking by Jain et al. (2014) which is contrary to classical queuing phenomenon named balking mentioned by Ancker and Gaffarian (1963a, b). Encouraged arrivals are different from reverse balking in the sense that reverse balking deals with probability calculated from existing system size and system capacity, while encouraged arrivals are directly related to the system size at given time or percentage increase in customers’ arrival due to offers and discounts. The phenomenon of encouraged arrivals is contrary to discouraged arrivals discussed by Kumar and Sharma (2012).

Once the customers are encouraged, they result in higher volumes to the system. High volumes result in longer queues. These queues can be physical or digital. Service facility experiences increased load and smooth functioning becomes a tedious task. A dissatisfactory service at this point may result in customer impatience and a customer may decide to abandon the facility. This phenomenon is termed as customer reneging and discussed first by Haight (1957). Reneging is a loss to business, goodwill of the company, and revenue. A number of papers emerged on impatient customers since the inception of concept. Bareer (1957) studied phenomenon of balking and reneging in many ways. Natvig (1974) derived transient probabilities of queueing system with arrivals discouraged by queue length. Dooran (1981) further discussed the notion of discouraged arrivals in his work. Xiong and Altiok (2009) discussed impatience of customers. Kumar and Sharma (2013, 2014) studied queuing systems with retention and discouraged arrivals. Kumar and Som (2014) study single-server stochastic queuing model with reverse balking and reverse reneging. They mentioned that customer impatience will also decrease with increase in volume of customers. Kumar and Som (2015a, b) further present a queuing model with reverse balking, reneging, and retention. Kumar and Som (2015a, b) further added feedback customers to their previous model. Recently, Som (2016) presented a queueing system with reverse balking, reneging, retention of impatient customers, and feedback with heterogeneous service. He discussed the case of healthcare facility going through mentioned contemporary challenges.

There is a need to have a strategy that can help in smooth functioning of the system for better result. Strategies driven by scientific methods in such cases result in better output. Owing to this practically valid aspect of business, we develop a single-server feedback stochastic queuing model addressing contemporary challenges in this paper. Cost–profit analysis of the model is discussed later.

2 Formulation of Stochastic Model

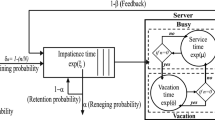
A Markovian single-server queuing model is formulated under the following assumptions:

  1. (i)

    The customers are arriving at the facility in accordance with Poisson process one by one with a mean arrival rate of \( \lambda + n \), where “n” represents the number of customers exists in the system.

  2. (ii)

    Customers are provided service exponentially with parameter \( \mu \).

  3. (iii)

    An FCFS discipline is followed.

  4. (iv)

    Service is provided through single server and the capacity of system is finite (say, N).

  5. (v)

    The reneging times are independently and exponentially distributed with parameter \( \xi \).

  6. (vi)

    Unsatisfied serviced customer may retire to the system with probability q and may decide to abandon the facility \( p = \left( {1 - q} \right) \).

  7. (vii)

    A reneging customer may be retained with probability \( q_{1} = \left( {1 - p_{1} } \right) \).

In order to construct a stochastic model based on assumptions (i)–(viii), the following differential-difference equations are derived. These equations govern exhaustive stages the system can experience. Equation (1) governs initial stage of the system, Eq. (2) governs the functioning stage, and Eq. (3) governs the stage when system is full. The three differential-difference equations governing the system are given by

$$ P_{0}^{{\prime }} \left( t \right) = - \lambda P_{0} \left( t \right) + \mu pP_{1} \left( t \right) $$
(1)
$$ P_{n}^{{\prime }} \left( t \right) = \left\{ {\lambda + \left( {n - 1} \right)} \right\}P_{n - 1} \left( t \right) + \left\{ {\left( { - \lambda + n} \right) - \mu p - \left( {n - 1} \right)\xi p_{1} } \right\}P_{n} \left( t \right) + \left( {\mu p + n\xi p_{1} } \right)P_{n + 1} \left( t \right) $$
(2)
$$ P_{N}^{{\prime }} \left( t \right) = \left\{ {\lambda + \left( {N - 1} \right)} \right\}P_{N - 1} \left( t \right) - \left\{ {\mu p + \left( {N - 1} \right)\xi p_{1} } \right\}P_{N} \left( t \right) $$
(3)

3 Steady-State Equations

In steady-state equation, the system of equations becomes

$$ 0 = - \lambda P_{0} + \mu pP_{1} $$
(4)
$$ 0 = \left\{ {\lambda + \left( {n - 1} \right)} \right\}P_{n - 1} + \left\{ {\left( { - \lambda + n} \right) - \mu p - \left( {n - 1} \right)\xi p_{1} } \right\}P_{n} + \left( {\mu p + n\xi p_{1} } \right)P_{n + 1} $$
(5)
$$ 0 = \left\{ {\lambda + \left( {N - 1} \right)} \right\}P_{N - 1} - \left\{ {\mu p + \left( {N - 1} \right)\xi p_{1} } \right\}P_{N} $$
(6)

4 Steady-State Solution

On solving above equations iteratively, we get

$$ P_{n} = \prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } $$

As normality condition explains \( \sum\nolimits_{n = 0}^{N} {P_{n} } = 1 \)

$$ P_{0} = \left\{ {1 + \sum\limits_{n = 1}^{N} {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}} } } \right\}^{ - 1} $$

And the probability that system is full is given by

$$ P_{N} = \prod\limits_{i = 0}^{N - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } $$

5 Measures of Performance

5.1 Expected System Size (Ls)

$$ L_{s} = \sum\limits_{n = 0}^{N} {nP_{n} } $$
$$ L_{s} = \sum\limits_{n = 0}^{N} n \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} $$

5.2 Expected Queue Length (Lq)

$$ L_{q} = \sum\limits_{n = 0}^{N} {\left( {n - 1} \right)P_{n} } $$
$$ L_{q} = \sum\limits_{n = 0}^{N} {\left( {n - 1} \right)} \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} $$

5.3 Average Rate of Reneging Is Given by (Rr)

$$ R_{r} = \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi p_{1} P_{n} } $$
$$ R_{r} = \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} $$

5.4 Average Rate of Retention Is Given by (RR)

$$ R_{R} = \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi q_{1} P_{n} } $$
$$ R_{R} = \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi q_{1} }}P_{0} } } \right\} $$

6 Numerical Illustration

Numerical validity of the model is tested by performing numerical analysis. The analysis is performed by varying parameters arbitrarily. Sensitivity of appropriate measures of performance is observed with respect to varying arbitrary values of parameters (Table 1).

Table 1 Variation in \( L_{s} ,L_{q} ,and\,R_{r} \) and \( R_{R} \) with respect to \( \lambda \). We take \( N = 10,\mu = 3,\xi = 0.2,q = 0.2,q_{1} = 0.3 \)
Full size table

We can observe that an increasing average rate of arrival leaves a positive impact on average system size; as a result queue length also increases, while increase in rate of reneging means that high volume of customers put service under pressure and lot of customers fail to wait after a threshold value of time and renege thereafter, i.e., abandon the facility without completion of service. The following graphs explain the phenomenon (Fig. 1).

Fig. 1
figure 1

Variation in system size and length of queue with respect to arrival rate

Full size image

Similarly, the numerical results are obtained by varying service rate and rate of reneging. The following tables explain the same (Table 2).

Table 2 Variation in \( L_{s} ,L_{q} ,R_{R} and\,R_{r} \) with respect to \( \mu \). We take \( N = 10,\lambda = 2,\xi = 0.2,q = 0.2,q_{1} = 0.3 \)
Full size table

We can observe as service rate increases, the expected system size decreases and so does expected length of queue, while decrease in rate of reneging, it means that decreasing volume of customers eases out the pressure on service and high number customers choose to wait rather than leaving the facility. The following graphs explain the phenomenon (Fig. 2).

Fig. 2
figure 2

System size and queue length with respect to service rate

Full size image

From Table 3, it can be observed that feedback results in increasing expected system size and queue length. The rate of reneging goes high as more and more customers in the system cause high level of delays in service and cause high level of impatience.

Table 3 Variation in \( L_{s} ,L_{q} ,R_{R} and\,R_{r} \) with respect to q. We take \( N = 10,\lambda = 2,\xi = 0.1,\mu = 3,q_{1} = 0.3 \)
Full size table

From Table 4, it can be observed that retention leaves a positive impact on system size. Though the queue length increases, retaining impatient customers is an important phenomenon that leads to increased revenue at the end.

Table 4 Variation in \( L_{s} ,L_{q} ,R_{R} and\,R_{r} \) with respect to \( q_{1} \). We take \( N = 10, \lambda = 2, \xi = 0.1, \mu = 3, q = 0.2 \)
Full size table

7 Economic Analysis of the System

This section discusses the cost–profit analysis of the model. An algorithm is written for newly formulated functions of total expected revenue, total expected cost, and total expected profit for obtaining numerical outputs.

Total expected cost (TEC) of the model is given by

$$ TEC = C_{s} \mu + C_{h} L_{s} + C_{r} R_{r} + C_{L} \lambda P_{N} + + C_{f} qL_{S } + C_{R} R_{R} $$
$$ \begin{aligned} TEC & = C_{s} \mu + C_{h} \sum\limits_{n = 0}^{N} n \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ & \quad + C_{r} \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi p_{1} } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ & \quad + C_{L} \lambda \prod\limits_{i = 0}^{N - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } + + C_{f} \times q\sum\limits_{n = 0}^{N} n \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ & \quad + C_{R} \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi q_{1} } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ \end{aligned} $$

Total expected revenue (TER) of the model is given by

$$ TER = R \times \mu \times \left( {1 - P_{0} } \right) + R_{f} \times q \times L_{s} $$

Total expected profit (TEP) of the model is given by

$$ \begin{aligned} TEP & = R \times \mu \times \left( {1 - P_{0} } \right) + R_{f} \times q \times L_{s} - C_{s} \mu + C_{h} \sum\limits_{n = 0}^{N} n \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ & \quad + C_{r} \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi p_{1} } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} + C_{L} \lambda \prod\limits_{i = 0}^{N - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} + + C_{f} } \\ & \quad \times q\sum\limits_{n = 0}^{N} n \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} + C_{R} \sum\limits_{n = 1}^{N} {\left( {n - 1} \right)\xi q_{1} } \left\{ {\prod\limits_{i = 0}^{n - 1} {\frac{\lambda + i}{{\mu p + i\xi p_{1} }}P_{0} } } \right\} \\ \end{aligned} $$

where

\( C_{s} \) :

Cost of service,

\( C_{h} \) :

Holding cost of a customer,

\( C_{r} \) :

Cost of reneging,

\( C_{L} \) :

Cost of a lost customer,

\( C_{f} \) :

Cost of feedback,

\( R \) :

Revenue earned from each customer,

\( R_{f} \) :

Revenue earned from each feedback customer, and

\( C_{R} \) :

Cost of retention of a customer.

The cost model formulated above is translated into MATLAB, and numerical results are obtained for varying rate of arrival and service (Table 5).

Table 5 Variation in \( TEC,TER\,{\text{and}}\,TEP \) with respect to \( \mu \). We take \( N = 10, \lambda = 2, \xi = 0.1, C_{S} = 10, C_{l} = 15, C_{h} = 2, C_{f} = 50, C_{r} = 2, R = 500 \)
Full size table

Though the cost increases with increase in the rate of service, as service cost increases but due to reduced rate of reneging, the revenue goes high and firms profit keeps on increasing with an improving rate of service (Table 6).

Table 6 Variation in \( TEC, TER {\text{and}} TEP \) with respect to \( \mu \). We take \( N = 10, \mu = 3, \xi = 0.1, C_{S} = 10, C_{l} = 15, C_{h} = 2, C_{r} = 2, R = 500 \)
Full size table

The table shows an increase in TEP with increase in average arrival rate which is obvious as increasing rate of arrival results in higher number of customers to the system and firm enjoys more revenue from each customer.

Figure 3 shows total expected profit is higher with improving service and fixed arrival (). In comparison to the case when arrivals increase, the customers are serviced at a constant rate. This shows an improving service that ensures better profits and a firm shall focus more on providing better service rather than bringing more customers to the system.

Fig. 3
figure 3

TEP with respect to fixed and improving service rate

Full size image

8 Conclusion and Future Scope

The results of the paper are of immense value for any firm encountering the phenomenon of encouraged customers and load on service. By knowing the measures of performance in advance, the overall performance of the system can be measured and an effective strategy can be planned for smooth functioning. By adopting and implementing this model, the economic analysis of the facility can also be measured and bird’s eye view on financial aspect of the business can also be observed.

Further optimization of service rate and system size can be achieved while the system can be studied in transient state. The system can also be studied for heterogeneous service. A multi-server model can also be explored.