An Improved Hybrid Offset-Based Min-Sum Decoding Algorithm

Abstract

In this work, a new hybrid approach based on offset min-sum decoding algorithm is proposed for decoding irregular low-density parity-check (LDPC) codes. In the proposed algorithm, incorporations are made in both the nodes of the Tanner graph with varying error correcting factors. In addition, to the error correcting factors, an adaptive weighting factors are utilized in CNU and VNU process to mitigate the numerical instabilities and negative correlation effects. These modifications in turn enhance the error correcting performance, which ultimately results in a better decoding efficiency. Through exhaustive simulation and comparison, it is shown that the proposed algorithm with a six-bit non-uniform quantization scheme exhibits good error correcting outcome at BER of 10⁻⁵ with an acceptable computational complexity.

1 Introduction

Low-density parity-check (LDPC) codes [1] have been a revelation in the field of error control coding (ECC) since their comeback in early 1990s [2]. In the current scenario of LDPC decoding, the min-sum algorithm (MSA) [3] and its variants are widely employed for better noise immunity and efficient hardware realization. An innovative approach in MSA is proposed by utilizing two different modification factors in check node process (MNMSA) [4]. This methodology uses the theory of order statistics to derive suitable modification factor to enhance the bit error rate (BER) performance. This method is enhanced to a certain extent by utilizing self-adaptive error correction factors (SAMSA) instead of order statistics [5]. This process achieves good reduction in computational complexity compared to [4]. Even though this process has fewer merits, it is not preferred for larger codeword length and irregular LDPC codes. The simplified version of 2D-MSA (SDMSA) [6] is proposed with an objective to achieve good error correcting performance with minimal numerical instability. Furthermore, in this numerical instability is reduced by replacing conventional multiplication operations with addition and shifting operations. Recently, an improvement to MSA using density evolution (IMSA) was proposed by Wang et al. [7]. This algorithm has a twofold approach, first was by utilizing probability density function to calculate the suitable error correction factor. Then, the selected error correction factor is calculated using the weighted average. In summary, these algorithms show that by utilizing different methodologies ranging from high-order statistics to probability density function achieves better improvement in error correcting performance and complexity reduction. However, these algorithms do suffer from severe error floors when decoded with larger block length irregular LDPC codes.

In this paper, an improved hybrid algorithm based on [8] is presented. In order to subdue the shortcomings of the former algorithms, some new incorporations are carried out in both the nodes of bipartite graph, i.e., check node unit (CNU) and variable node unit (VNU). In general, the magnitude overestimation issue occurs when a single decoding algorithm is used to decode multiple codeword lengths of irregular LDPC codes. This often results in numerical instabilities which increases the requirement for more decoding iterations. To overcome this drawback, multiple error correction factors, along with iteration dependent compensation (weighting) factors are employed in the CNU. These error correcting factors are adaptive and are dynamically used on the switching basis to enhance the convergence speed. Also, in the bit node update process along with error correction factor a penalty (weighted) factor is used to minimize the negative correlation effects of the iterative information updating process. However, the usage of weighting factors enhances the computational complexity moderately. Furthermore, this proposed algorithm is shown to be compatible with different types of irregular LDPC codes with varying code length and rates. Also, this decoding algorithm can be employed in designing resource efficient multi-standard LDPC decoders.

2 Framework

In general, let the set of variable nodes associated to the cth check node be N(c), and the subset excluding the νth bit node from N(c) be denoted as N(c)\ν. Similarly, the set of check nodes connected to the νth bit node be M(ν), and the subset excluding the cth check node from M(ν) be denoted as M(ν)\c The following notations are utilized to signify the decoding process:

L_ch: The log-likelihood ratio (LLR) information according to the received channel value.

$\alpha_{cv}^{(i)}$: The outgoing LLR data from check node c to variable node ν.

$\beta_{vc}^{(i)}$: The outgoing LLR information from variable node ν to check node c.

$\beta_{v}^{(i)}$: Aposteriori LLR information computed at each iteration.

$h_{n}^{T} = (h_{n,1} ,h_{n,2} , \ldots ,h_{n,N} )$ n = 1, 2, …, N: Rows of the H matrix.

$\sigma_{{d_{c} (m)}}^{(i)}$: Offset factor for check node update processing.

$\theta_{{d_{c} (m)}}^{(i)}$: Iteration dependent weighting factor.

$\zeta_{{d_{c} (m)}}^{(i)}$: Stifling factor in check node processing.

$\xi_{{d_{c} (m)}}^{(i)}$: Optimally adaptive offset factor for CNU.

$\delta_{{d_{\nu } (n)}}^{(i)}$: Offset factor for variable node processing.

$\mu$: Iteration dependent penalty factor for variable node.

2.1 Decoding Methodology of the Proposed Algorithm

The decoding flow of the proposed algorithm is described briefly below

Step 1: Initialization Process

$$ \beta_{\nu c}^{(0)} = L_{ch} $$

(1)

Step 2: Check node function

$$ \alpha_{c\nu }^{(i)} = \prod\limits_{n \in N(c)\backslash \nu } {\text{sgn} (\beta_{nc}^{(i - 1)} ) \cdot \hbox{max} (\theta_{{d_{c} (m)}}^{(i)} \cdot \mathop {\hbox{min} }\limits_{n\varepsilon N(c)\backslash \nu } } \left| {\beta_{nc}^{(i - 1)} } \right| - \sigma_{{d_{c} (m)}}^{(i)} ,0) $$

(2)

Message stifling if $\left( {h_{n}^{T} \cdot x\, = \, = \, 1 {\text{ mod 2}}} \right)$, where x = sign $(\beta_{v}^{(i)})$

$$ \alpha_{c\nu }^{\prime (i)} = \prod\limits_{n \in N(c)\backslash \nu } {\text{sgn} (\beta_{nc}^{(i - 1)} ) \cdot \hbox{max} \left( {\mathop {\hbox{min} }\limits_{n \in N(c)\backslash \nu } \left| {\beta_{nc}^{(i - 1)} } \right| - \xi_{{d_{c} (m)}}^{(i)} ,0} \right)} $$

(3)

$$ {\text{where}}\;\zeta_{{d_{c} (m)}}^{(i)} = \left( {1 + \zeta_{{d_{c} (m)}}^{(i)} } \right) \cdot \sigma_{{d_{c} (m)}}^{(i)} $$

(4)

Step 3: Bit node function

$$ \beta_{\nu c}^{\prime (i)} = \beta_{\nu c}^{(0)} + \text{sgn} \left\{ {\sum\limits_{m \in M(\nu )\backslash c} {\alpha_{m\nu }^{(i)} - \alpha_{m\nu }^{\prime (i - 1)} } } \right\} \cdot \hbox{max} \left\{ {\left| {\sum\limits_{m \in M(\nu )\backslash c} {\alpha_{m\nu }^{(i)} - \alpha_{m\nu }^{\prime (i - 1)} } } \right| - \frac{{\delta_{{d_{\nu } (n)}}^{(i)} }}{\mu }} \right\} $$

(5)

$$ \beta_{\nu }^{\prime (i)} = \beta_{\nu c}^{(0)} + \text{sgn} \left\{ {\sum\limits_{m \in M(\nu )} {\alpha_{m\nu }^{(i)} - \alpha_{m\nu }^{\prime (i - 1)} } } \right\} \cdot \hbox{max} \left\{ {\left| {\sum\limits_{m \in M(\nu )} {\alpha_{m\nu }^{(i)} - \alpha_{m\nu }^{\prime (i - 1)} } } \right| - \frac{{\delta_{{d_{\nu } (n)}}^{(i)} }}{\mu }} \right\} $$

(6)

Step 4: Judge and terminate using end conditions

If ($H^{T} \cdot \widehat{c} = = 0$) output x and the decoding process is terminated.

3 Simulation Results

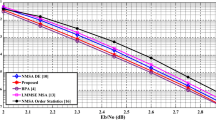
In order to validate the decoding efficiency of the proposed methodology, two different irregular rate 1/2 LDPC codes belonging to Wi-MAX and WLAN standards have been considered, respectively. Figures 1 and 2 show the error correcting performance of the proposed algorithm and its comparison with few recent decoding algorithms. For performance comparison purposes, the maximum decoding iterations are fixed at 10 and a six-bit non-uniform quantization scheme is adopted. Furthermore, in the proposed decoding algorithm with the error correction factor values are found using heuristic simulations [9] and are found to be $\left( {\alpha_{{d_{c} (m)}}^{(i)} ,\xi_{{d_{c} (m)}}^{(i)} ,\delta_{{d_{\nu } (n)}}^{(i)} } \right)\, = \,\left( {0. 2 1, \, 0. 3 3, \, 0. 3 7} \right)$ for rate 1/2, Wi-MAX Standard and (0.18, 0.29, 0.33) for rate 1/2, WLAN Standard irregular LDPC code, respectively. In light of results illustrated in Figs. 1 and 2, it is clearly evident that the proposed scheme outperforms the recently proposed schemes convincingly in terms of BER when measured at BER of 10⁻⁵. Therefore, clearly it is demonstrated using experimental simulations that the proposed hybrid scheme achieves better error correction phenomenon with only a small increase in the implementation complexity. This outstanding error correcting phenomenon trait exhibited with irregular LDPC codes of larger codeword length is clearly suited for many emerging wireless communication standards.

Fig. 1

BER plots for the rate 1/2 (2304,1102) irregular LDPC codes of Wi-MAX standard

Fig. 2

BER plots for the rate 1/2 (1944,972) irregular LDPC codes of WLAN standard

4 Conclusion

In this paper, an improved hybrid offset decoding algorithm based on adaptive weighting factors is introduced. The proposed methodology is applied to irregular LDPC codes belonging to Wi-MAX and WLAN standard. Through exhaustive simulations, it is clearly seen that the intended algorithm can achieve considerable coding gain improvement with minimum increase in the computational complexity. By analyzing the performance with recent MSA-based decoding algorithms, the proposed scheme exhibit better decoding efficiency without any additional implementation overhead.