Keywords

1 Introduction

A nondestructive testing (NDT) of damage identification for Structural Health Monitoring (SHM) is important in industrial applications. The main purpose to use X-IGA is easy for any application by keeping the same discretization and we can put any crack for any position without remeshing as in case Finite Element Method (FEM). In previous studies, fracture mechanic tests of shells and plates structures were focused on in-plane tensile loading as described by Moës et al. [1]. A crack in thin shells was simulated using Finite Element Method (FEM) and Continuous Re-meshing (CR), and the direction of crack propagation was simulated from the fracture analysis of thin plates as presented by Potyondy et al. [2]. Many fracture mechanics problems are solved using XFEM for thick plates by Dolbow et al. [3]. The plane fracture mechanics problems was analyzed by Benson et al. [4] using XIGA technique. The dynamic of fracture in Kirchhoff plate and shell using XFEM technique was used by Rouzegar and Mirzaei [5]. Chatzi et al. [6] presented several improvements using XFEM–GA algorithm for detecting and locating different types of flaw of any shape. The experimental validation is used for detecting the location of crack in plate. A numerical model of cracked plate using X-IGA technique by introducing the different loads and boundary conditions was presented by Bhardwaj et al. [7].

The fracture mechanics simulation in bi-layered FGMs using XIGA technique was presented by Bhardwaj et al. [8]. A nondestructive testing (NDT) technique using XFEM coupled with Genetic Algorithms (GAs) was proposed by Rabinovich et al. [9]. In this application, it was shown that cracks in flat membranes could efficiently be detected using dynamic and static tests. Tran Vinh et al. [10] presented a new and effective formulation. The objective was to combine XIGA technique and Higher-order Shear Deformation Theory (HSDT) to study the free vibration of cracked plates.

Habib et al. [11] used the X-IGA technique for modeling the crack in orthotropic plate. The orthotropic cracked tip enrichments was used to reproduce the singular fields near a crack tip, and fracture mechanics properties of the models were defined by the mixed mode stress intensity factors (SIFs) obtained by means of the interaction integral (M-integral). The double notch crack identification in carbon fiber reinforced polymer (CFRP) using reduced model based on Proper Orthogonal Decomposition (POD) coupled with Radial Basis Function (RBF) and combined with Genetic Algorithm (GA) and Cuckoo Search (CS) algorithm, was presented by Samir et al. [12]. The problem of delamination was detected using Virtual crack closure technique (VCCT) using modal flexibility based on dynamic analysis was presented by Khatir et al. [13]. Benaissa et al. [14] presented an application for crack identification plate with different type of structure using POD coupled with RBF using Particle Swarm Optimization (PSO) as inverse problem. In the previous research, Waisman et al. [15] used the XFEM combined with GA application for detecting the flaws in elastostatics. The XFEM enrichment functions were chosen to model strong and weak discontinuities arising from straight cracks and circular holes. Using these applications, the hole and crack was detected using XFEM with higher accuracy.

This paper is organized as follows: The implementation of X-IGA for crack location in the plate is described in Sect. 2. Then in Sect. 3, Particle Swarm Optimization (PSO) combine with X-IGA for crack identification is presented. Subsequently, several numerical simulations are illustrated in Sect. 4 in order to demonstrate the robustness and efficacy of proposal application for Crack identification using PSO. Finally, concluding remarks are presented in Sect. 5.

2 Motivation and X-IGA Approach in Forward Problem

To analyze the problems in mechanical structures, XFEM with IGA, known also as extended isogeometric analysis (X-IGA), is proposed. The XFEM technique is an effective tool to analyze the statics and dynamics problems in the structures whereas IGA is efficient for analyzing the complex geometries. The control points influenced by geometric discontinuities using XIGA technique are locally enriched to capture singularities produced in the solution. Also, crack face and crack tip are enriched by Heaviside functions and crack tip functions, respectively.

2.1 A Brief of B-Spline/NURBS Functions

A knot vector \( \Xi = \left\{ {\upxi_{1} \,\upxi_{2} , \ldots ,\,\upxi_{{{\text{n}} + {\text{p }} + 1}} } \right\} \) is a non-decreasing sequence of parameter values ξi, i = 1, …, n +p.

Where:

  • ξi ∈ R called ith knot lies in the parametric space,

  • p: is the order of the B-spline,

  • n: is number of the basis functions.

$$ N_{i,0} \left( \xi \right) = \left\{ {\begin{array}{*{20}c} 1 & {if} & {\xi_{i} \le \xi < \xi_{i + 1} } \\ 0 & {} & {Otherwise} \\ \end{array} } \right. $$
(1)

For p ≥ 1,

$$ N_{i,p} \left( \xi \right) = \frac{{\xi - \xi_{i} }}{{\xi_{i + p} - \xi_{i} }}N_{i,p - 1} \left( \xi \right) + \frac{{\xi_{i + p + 1} - \xi }}{{\xi_{i + p + 1} - \xi_{i + 1} }}N_{i + 1,p - 1} \left( \xi \right) $$
(2)

For some curved geometries such as circles, cylinders and spheres, the Non-Uniform Rational B-Splines (NURBS) functions are used. Being different from B-spline, each control point of NURBS has additional value called an individual weight wi [16]. The NURBS functions can be presented as following:

$$ R_{i} \left( {\xi ,\eta } \right) = \frac{{N_{i} w_{i} }}{{\mathop \sum \nolimits_{i}^{m \times n} N_{i} \left( {\xi ,\eta } \right)w_{i} }} $$
(3)

2.2 XIGA Implementation

To capture the local discontinuous and singular fields in fracture mechanics, the enriched functions are added according to ideas from XFEM as follows:

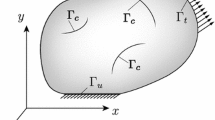
$$ u^{h} \left( {\text{x}} \right) = \sum\nolimits_{{I{ \upepsilon }S}} {R_{I} \left(\upxi \right)q_{I}^{std} } + \sum\nolimits_{{J{ \upepsilon }S^{enr} }} {R_{J}^{enr} } \left(\upxi \right)q_{J}^{enr} $$
(4)

In which, the NURBS basis functions are utilized instead of the Lagrange polynomials to create eXtended IsoGeometric Analysis (XIGA) [10, 17, 18]. The functions \( R_{J}^{enr} \) are the enrichment functions associated with node J located in enriched domain Senr that is split up into two parts including: the first set Sc for Heaviside enriched control points and the second present a set Sf for crack tip enriched control points as presented in Fig. 1. The discontinuous displacement field depend the enrichment function as presented in the following function:

$$ R_{J}^{enr} (\upxi) = R_{J} (\upxi )\left( {{\text{H}}({\text{x}}) - {\text{H}}\left( {{\text{x}}_{\text{J}} } \right)} \right),{\text{J}}\ \upepsilon \ {\text{S}}^{\text{c}} $$
(5)
Fig. 1.
figure 1

The nodal sets Sc, Sf for a quadratic NURBS mesh.

Full size image

Where, H(x) is the Heaviside function.

The singularity field near crack tip is modified by the branching functions as follows [19]:

$$ R_{J}^{enr} (\upxi) = R_{J} (\upxi)\left( {\sum\nolimits_{L = 1}^{4} {(G_{L} ( {r,\uptheta} ) - G_{L} ( {r_{J } ,\uptheta_{J} } ))} } \right),{\text{J}}\ \upepsilon \ {\text{S}}^{f} $$
(6)

Where:

$$ G_{L} \left( {r,\uptheta} \right) = \left\{ {\begin{array}{*{20}c} {r^{{\frac{3}{2}}} [\sin \frac{\uptheta}{2}\cos \frac{\uptheta}{2}\sin \frac{{3\uptheta}}{2}\cos \frac{{3\uptheta}}{2}]} \\ {r^{{\frac{1}{2}}} [\sin \frac{\uptheta}{2}\cos \frac{\uptheta}{2}\sin \frac{\uptheta}{2}{\text{sin }}\uptheta\,{ \cos }\frac{\uptheta}{2}\cos\uptheta]} \\ \end{array} } \right. $$
(7)

Where r and Ɵ are represented in the local coordinates of the crack tip.

The evaluation of crack tip enriched control points based on the parametric coordinate of the crack tip are evaluated and the NURBS basis functions corresponding to these parametric coordinates are calculated. The non-zero NURBS values are specified at the crack tip enriched control points. The enriched domain according the crack tip changes with the variation in NURBS order. Heaviside enriched control points are evaluated using the same procedure for the crack tip.

For the test of mode II, closed form displacements are given by:

$$ u_{x} \left( {{\text{r}},\uptheta} \right) = \frac{{K_{II} }}{2\mu }\sqrt {\frac{r}{2\pi }} \,{ \sin }\,\frac{\uptheta}{2}\left( {k + 1 + 2\,cos^{2} \frac{\uptheta}{2}} \right) $$
(8)
$$ u_{y} \left( {{\text{r}},\uptheta} \right) = \frac{{K_{II} }}{2\mu }\sqrt {\frac{r}{2\pi }} \,{ \cos }\frac{\uptheta}{2}\left( {k + 1 + 2\,sin\frac{\uptheta}{2}} \right) $$
(9)

where KII = σ√πa is the mode II stress intensity factor, and the mode II stress field is given by:

$$ \sigma_{xx} \left( {{\text{r}},\uptheta} \right) \, = \frac{{K_{II} }}{{\sqrt {2\pi r} }}\,{ \sin }\frac{\uptheta}{2}\left( {2 + cos\frac{\uptheta}{2}cos\frac{{3\uptheta}}{2}} \right) $$
(10)
$$ \sigma_{yy} \left( {{\text{r}},\uptheta} \right) \, = \frac{{K_{II} }}{{\sqrt {2\pi r} }} { \sin }\frac{\uptheta}{2}cos\frac{\uptheta}{2}cos\frac{{3\uptheta}}{2} $$
(11)
$$ \sigma_{xy} \left( {{\text{r}},\uptheta} \right) = \frac{{K_{II} }}{{\sqrt {2\pi r} }} { \cos }\frac{\uptheta}{2}\left( {1 - sin\frac{\uptheta}{2}sin\frac{\uptheta}{2}} \right) $$
(12)

3 Particle Swarm Optimization (PSO)

In this section, we used PSO coupled with XIGA plate for crack identification based on II mode testing as inverse problem. In PSO, each candidate solution is called a “particle” and represents a point in a D-dimensional space, if D is the number of parameters to be optimized according to the problem. Accordingly, the position of the ith particle may be described by the vector xi as:

$$ {\text{x}}_{\text{i}} = \, \left[ {{\text{x}}_{\text{i1,}} {\text{x}}_{\text{i2,}} {\text{x}}_{\text{i3,}} {\text{x}}_{{{\text{i4,}} \ldots ,}} {\text{x}}_{\text{iD}} } \right] $$
(13)

The population of N candidate solutions constitutes the swarm:

$$ {\text{X}} = \left\{ {{\text{x}}_{ 1 ,} {\text{x}}_{ 2 ,} {\text{x}}_{3, \ldots ,} {\text{x}}_{4} } \right\} $$
(14)

To search the best optimal solution according the problem, the particles define trajectories of the updated position iteratively based on the following equation:

$$ {\text{x}}_{\text{i}} \left({{\text{t}} + 1} \right) \, = {\text{ x}}_{\text{i}} \left({\text{t}} \right) + {\text{ v}}_{\text{i}} \left({{\text{t}} + 1} \right) $$
(15)

Where:

  • t and t + 1 presents two successive iterations of the algorithm and vi is the vector collecting the velocity.

The velocity vectors govern the way particles move across the search space and are made of the contribution of three terms:

  1. 1.

    Defining the inertia from drastically changing direction, by keeping track of the older flow direction.

  2. 2.

    The cognitive component accounts for the tendency of particles to return to their own previously found best positions.

  3. 3.

    The social component identifies the propensity of a particle to move towards the best position of the whole swarm.

The velocity of the ith particle is defined as:

$$ {\text{v}}_{\text{i}} \left( {{\text{t}} + 1} \right) = {\text{ v}}_{\text{i}} \left( {\text{t}} \right) + {\text{c}}_{ 1} \left( {{\text{p}}_{\text{i}} - {\text{x}}_{\text{i}} \left( {\text{t}} \right)} \right){\text{R}}_{ 1} + {\text{c}}_{ 2} \left( {{\text{g}} - {\text{x}}_{\text{i}} \left( {\text{t}} \right)} \right){\text{R}}_{2} $$
(16)

Where:

  • pi: is personal best of the particle (the coordinates of the best solution),

  • g: is the global best (the overall best solution obtained by the swarm),

  • c1 and c2 are The acceleration constants 0 ≤ c1, c2 ≤ 4.

The constants R1 and R2 are two diagonal matrices of random numbers generated from a uniform distribution in [0,1], so that both the social and the cognitive components have a stochastic influence on the velocity update rule in Eq. (16). The trajectories drawn by the particles randomly in nature, as they derive from the contribution of systematic attraction towards the personal and global best solutions and stochastic weighting of these two acceleration terms. In addition, the fixed PSO parameters are given for the following simulations; that is, the population size N = 20, generation number Gn = 20, inertia weight w = 0.5, and two constants c1 = c2 = 2.

In SHM, it is impossible to know the crack position and measure it’s length directly because in the majority of cases it is embedded. Therefore, we rely on directly measurable data to reach the crack information. In this study, we used the boundary displacement. Our problem is formulated as inverse problem, where the PSO is responsible for generating multiple cracks and compare their corresponding boundary displacement to the Unique one of the crack that we want to identify (measured displacement).

Since the proposed method relays on the nodal displacement, all boundary nodes are considered as sensor point. We consider data from sensors by obtaining the displacement results from the nodes chosen as sensors point. Figure 2 depicts an example of the controlled plate using 10 strain sensors. The sensitivity of displacement used according the position of the strain gauges in the nodes 1–5 and 307–311 in two directions X and Y.

Fig. 2.
figure 2

Mesh of 18 × 18 cubic NURBS elements.

Full size image

The main purpose of using PSO in this paper is to identify a crack in a plate by an inverse problem using as input the displacements around X and Y to compare the displacement between measured and predicted by PSO. The objective function is presented in the following equation:

$$ \varPi = Abs\,\left[ {\left[ {\begin{array}{*{20}c} {Measured\,displacements } \\ {\left[ {\begin{array}{*{20}c} {Disp\left( {x_{1} } \right)} \\ \vdots \\ {Disp\left( {x_{10} } \right)} \\ \cdots \\ {Disp\left( {y_{1} } \right)} \\ \vdots \\ {Disp\left( {y_{10} } \right)} \\ \end{array} } \right]} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {Predicted\,displacement} \\ {\left[ {\begin{array}{*{20}c} {Disp\left( {x_{1} } \right)} \\ \vdots \\ {Disp\left( {x_{10} } \right)} \\ \cdots \\ {Disp\left( {y_{1} } \right)} \\ \vdots \\ {Disp\left( {y_{10} } \right)} \\ \end{array} } \right]} \\ \end{array} } \right]} \right] $$
(17)

Where: \( \varPi \) is the difference in displacements between measured and predicted by PSO:

$$ Obj_{func} = \sum\nolimits_{1}^{n} \varPi \quad {\text{n}} = 20\,\left( {\text{Line number}} \right) $$
(18)

If the \( {\text{measured displacements }} = {\text{predicted displacement}} \)

$$ Obj_{func} = 0 $$
(19)

4 Numerical Results

We used different scenarios for crack identification varying the position of the crack and its length, in a square specimen under mode II fracture test. PSO was used for solving the inverse crack identification problem in the scenarios listed below. For each case, the optimization process was run 4 times and the computation was stopped when the number of iterations of 20 was reached.

4.1 Cracked Plate - Scenario 1

In this case, the crack is positioned at the center at the left edge at P = 0.5 m, and its length is considerably long at value of a = 0.5 m, which is half the width of the specimen. The deformed shape is presented in Fig. 3. Figure 4(a) and (b) show, respectively, the convergence of crack position and length and the convergence of the fitness value. Results shows that the crack was accurately identified after 20 iterations with position 0.493 m and length 0.514 m.

Fig. 3.
figure 3

The deformed shape based on cracked plate - scenario 1

Full size image
Fig. 4.
figure 4

Crack identification using PSO - scenario 1

Full size image

4.2 Cracked Plate - Scenario 2

For this scenario, the position of crack is the same as the first scenario P = 0.5 m and with a smaller crack length a = 0.25 m as shown in Fig. 5. The crack identification results are presented in Fig. 6(a) and (b), in which is shown that the estimation is accurate.

Fig. 5.
figure 5

The deformed shape based on cracked plate of scenario 2

Full size image
Fig. 6.
figure 6

Crack identification using PSO based, cracked plate - scenario 2.

Full size image

4.3 Cracked Plate - Scenario 3

In this case the crack is of medium size of a = 0.33 m, and position in a lower position at P = 0.33 m. The deformed shape after mode II loading is presented in Fig. 7. The crack length and position identification is presented in Fig. 8, in which it is shown that the crack is identified correctly with little less accuracy than the central crack.

Fig. 7.
figure 7

The deformed shape based on cracked plate of scenario 3

Full size image
Fig. 8.
figure 8

Crack identification using PSO - scenario 3.

Full size image

4.4 Cracked Plate - Scenario 4

In this last case the crack is at the lowest position at P = 0.25 m and the smallest size with a = 0.20 m, as presented in Fig. 9. The identified results are depicted in Fig. 10, where it can be seen that the algorithm is able to identify the crack with considerable accuracy.

Fig. 9.
figure 9

The deformed shape based on cracked plate of scenario 4.

Full size image
Fig. 10.
figure 10

Crack identification using PSO based on scenario 4.

Full size image

Generally, the proposed approach XIGA-PSO based on displacement of 10 sensor points, is able to predict the crack parameters accurately, in the considered scenarios of fracture mechanics test. Only 20 PSO iterations is enough to reach estimation minimum accuracy of 90% iteration. The worst and best accuracy of crack length are presented respectively, as 95% for scenario 1 and 98.6 for scenario 4. The best accuracy of position is presented in scenario 2 with 98.9% accuracy and of worst accuracy is presented in scenario 1 with 97.74%.

5 Conclusion

New application has been proposed for two-dimensional extended isogeometric finite element analysis for solid and structural mechanics. In this paper, a non-destructive method for the estimation of both the location and the length of a crack in plate under mode II fracture mechanics test was considered. The PSO is coupled with XIGA based on inverse problem using displacement of mode II loading using 10 strain sensors. The objective function compares the calculated and the predicted displacements. The results show that the estimation of the crack position and length was accurate.